摩托车保险杠振动分析与优化设计

雷 鹏， 黄国鹏， 王 兵， 欧欣然

(隆鑫通用动力股份有限公司， 重庆 400052)

摩托车保险杠作为一种机械防护装置，它通过自身的强度和支撑力，避免车辆发生意外翻倒后对人员造成挤压或者剐蹭伤害，同时保护车辆的外观覆盖件，是车辆安全行驶的重要保障[1-3]。车辆在行驶过程中，会受到来自发动机和路面的激励，而欠佳的保险杠结构设计，使得零部件的固有频率过低，不仅影响摩托车的骑乘体验和操稳控制，还有可能与发动机等主要振动源的激励频率耦合，导致保险杠振动过大而发生疲劳破坏以及结构性断裂，缩短其使用寿命，增加更换的频次[4-7]。更有甚者，保险杠不仅无法在关键时候起到缓冲作用，以保护车辆和骑行人员安全，相反还会对骑行人员造成二次伤害。因此，对保险杠采取一定的抗震措施和结构设计优化，避免发生共振，提高其抗震性能非常有必要。

随着计算机辅助技术的快速发展和成熟，因模态分析具有可视性强、操作方便和成本较低等优点，已经被广泛地应用于刚性系统结构的振动分析与控制工程中。洪金涛等[8]基于模态分析对某商用车前保险杠进行振动特性预测和模态改进贡献量分析，明确保险杠方案设计的优化方向；徐中明等[9]采用拓扑优化技术，对某乘用车的保险杠进行结构优化，为保险杠的截面形状和板件厚度提供最优设计参数；展新等[10]分析了载货货车保险杠结构特性和动态谐振响应机理，研究了保险杠结构的避频解耦合振动能量损耗能力，为保险杠的工程试验提供理论支撑。由此可见，模态分析技术已经成为研究机械系统或零部件振动特性的主要技术手段。上述文献关于保险杠的振动控制与研究基本都集中在汽车领域，但鲜有关注摩托车上安装保险杠的振动问题，由于结构设计与安装位置的差异，摩托车保险杠与驾驶员尤其是其腿部近距离接触，其振动问题将给驾乘人员带来更大的行车安全隐患，因此，有必要对摩托车保险杠进行振动分析与优化设计，从而降低保险杠的振动，提升车辆的舒适性。

某原理样车在道路试验阶段，试制车辆出现前保险杠剧烈抖动问题，对整车的行驶带来较大的安全隐患。为了解决该问题，结合计算机辅助工程和测试分析的技术手段，着力于对摩托车保险杠进行结构分析和优化设计。主要的技术思路为：基于Hyper Mesh对保险杠进行模态分析，计算其固有频率和振型；基于LMS Test.Lab测试系统对保险杠进行振动测试，用振幅曲线描述其振动特征；结合模态分析结果和振动测试结果，找出摩托车保险杠振动剧烈的原因，有针对性地对保险杠的结构进行优化设计。最后，对优化设计后的样车进行试验验证和主观评价，验证优化设计的振动控制效果。本文研究可为企业解决类似的工程问题提供理论参考，研究结果具有较强的工程化意义和实际生产价值，可直接应用于摩托车保险杠的结构设计与优化。

1 振动原因分析与诊断

1.1 原保险杠振动测试

为准确地了解摩托车保险杠的动态响应情况，采用LMS Test.Lab测试分析系统，对其进行振动测试与分析，用振动频谱描述其振动特征[11]。为研究仅为发动机激励条件下摩托车保险杠的振动响应，在底盘测功机上对该车保险杠进行振动试验，试验工况设置为发动机转速2 000～8 000 r/min的匀加速过程，用以模拟车辆保险杠在道路试验过程中的真实振动响应。因保险杠左右对称，仅沿着保险杠右侧布置振动加速度传感器。坐标系规定为：+X(车辆向前)，+Y(车辆向前左侧)，+Z(竖直向上)[12]。摩托车保险杠振动测点的布置如图1所示。

图1 原车保险杆振动测点布置

振动加速度传感器采集的是保险杠三维方向的振动信号，重点关注的是其Z向和X向的振动情况。图2为保险杠的振幅曲线。从图2中可以看出，保险杠在5 600 r/min存在明显的共振特征，其振幅急剧放大，其中Z向振幅最高达31g，X向振幅最高达4g，对应的1阶模态频率均为93 Hz，其余转速段振幅变化均较为平缓。

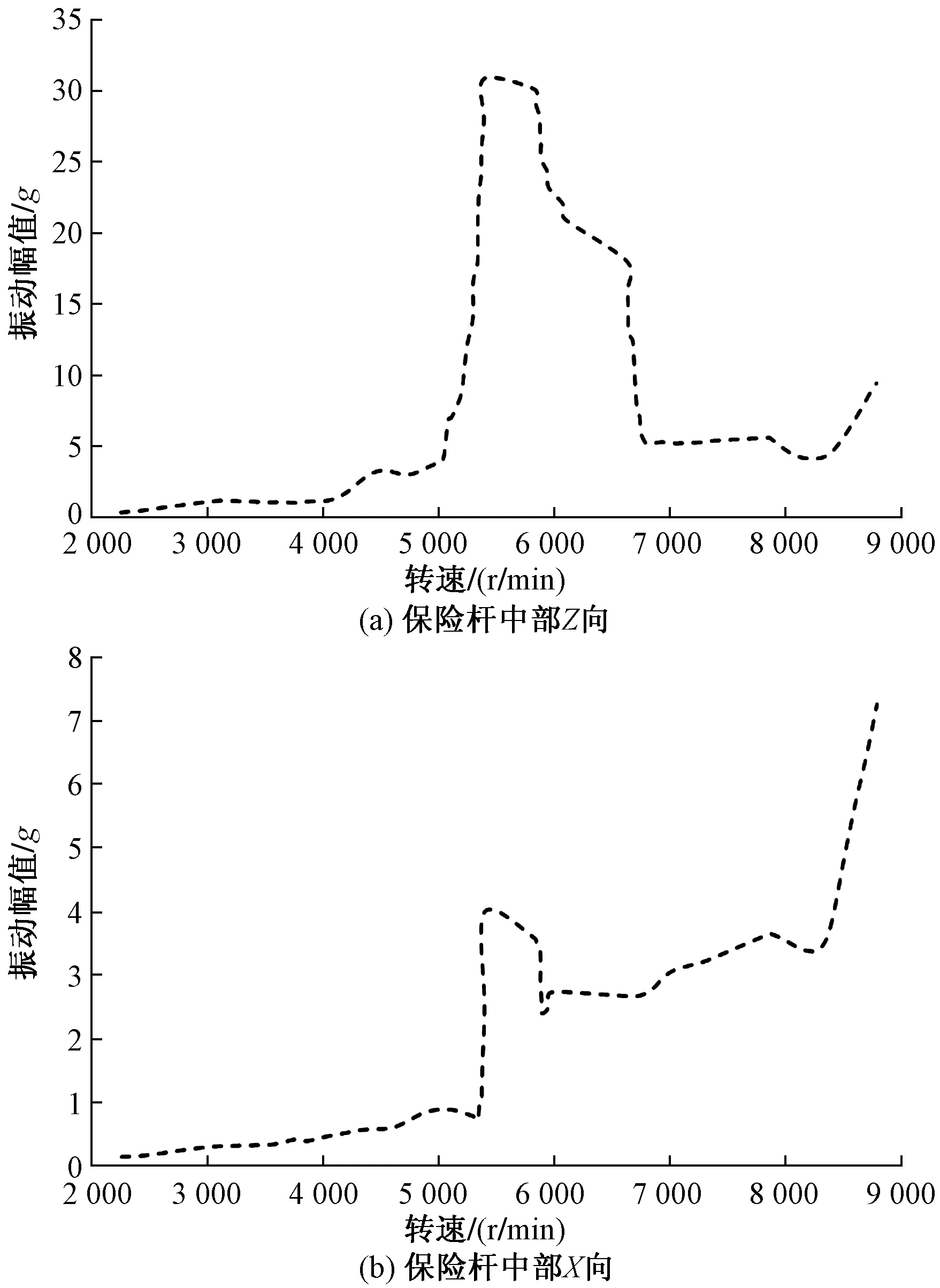
图2 原保险杠振幅曲线

1.2 模态分析理论基础

对于车架而言，模态分析本质上是将车架结构简化为一多自由度模型。对某一线性系统，其动力学微分方程[13-15]可表示为

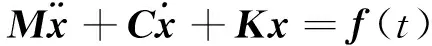
(1)

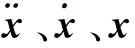
(2)

特征方程为

|K2-ω2M|=0

(3)

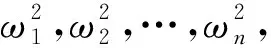
1.3 保险杠实际约束下的模态分析

图3所示为摩托车保险杠的几何模型。采用有限元软件Hyper Mesh对保险杠的CATIA模型进行有限元建模。该保险杆的主要结构为等壁厚圆管，与圆管的长度和截面尺寸相较而言，其厚度很小，故而采用Shell单元进行模拟，单元网格尺寸为4 mm。保险杠构件和安装支耳均是通过焊接连接在一起，建模时忽略焊缝的影响，各构件之间采用刚性单元MPC连接，同时创建材料的属性参数并进行关联[18-20]。单元材料选用Q235优质钢，其材料属性为：弹性模量E=2.05×105MPa，泊松比μ=0.3，密度ρ=7.85×103kg/m3。

图3 保险杠几何模型

根据构件边界条件的不同，模态分析分为自由模态和约束模态两种边界状态，其中约束模态是模拟构件在实际工况边界条件下的模态分析，同时考虑边界条件对模态频率的影响[21]。本文所研究的摩托车属于跨骑式车，其保险杠通过螺栓把上、下方的连接支耳安装在车架发动机悬挂下方，为了更加真实地反映保险杠的振动特性情况，在对保险杠进行模态分析时，以实际约束状态下的模态分析结果作为判定依据，约束边界具体如下：限制保险杆上、下方安装支耳6个方向的自由度，模拟保险杆被螺栓完全固定到车架上。摩托车保险杠前5阶模态计算结果见表1。保险杠的第1阶模态频率对应的振型图如图4所示，对应模态频率为94 Hz，其振型表现为保险杠前后摆动，最大变形发生在保险杠两侧中部。

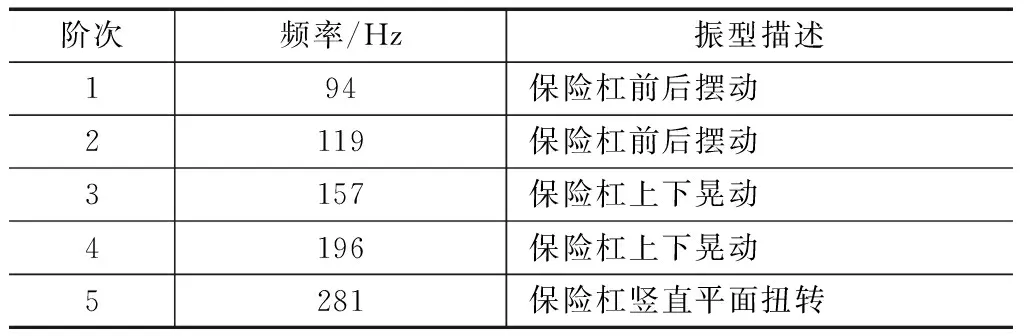
表1 摩托车保险杠前5阶固有频率和振型

图4 保险杠第1阶模态频率(94 Hz)对应的振型图

1.4 保险杠振动原因诊断

结合图2保险杠的测试结果可以看出，振幅曲线在5 600 r/min存在明显的共振，对应的一阶频率为93 Hz，该频率和保险杠自身的1阶频率94 Hz相接近，在发动机激励下发生共振，导致保险杆的振幅急剧增大，由此可以判断，保险杠的1阶模态频率是引起自身振动剧烈问题的主要原因。摩托车保险杠振动测试结果和模态分析结果，两者对保险杠振动特性的描述是吻合的，保险杆建模与简化合理，计算结果可靠，可用于对保险杆进行振动特性分析与优化设计。

2 保险杠结构优化设计

2.1 优化设计方案

保险杠的刚度直接影响其模态分布，要抑制保险杠对振动的响应，提高保险杠的抗振能力，主要是寻求通过改变保险杆刚度的途径加以解决。影响保险杠刚度的因素主要包括：保险杠的结构设计、保险杠的规格尺寸、保险杠的材料属性等[22]。

结合表1保险杠的模态分析结果可知，保险杠第1阶模态频率为94 Hz，振型表现为保险杠的前后摆动，最大变形发生在保险杠中部。保险杠属于摩托车的非复杂构件，改变保险杠的设计尺寸和材料属性，无论是经济成本还是时间成本均过高，且对其模态频率的影响也十分有限。为了增强保险杆与车架之间的连接刚度，减弱保险杆在发动机激励下产生过大的响应和变形，基于方案实施的操作便捷性、企业开发周期及经济成本控制两方面考虑，对保险杆采取的优化方向是通过结构优化设计提高保险杠的连接刚度，使其模态频率提升，从而避开发动机的激振频率。详情方案实施如图5所示，具体为：在保险杠左、右两侧分别焊接2根φ18×2的优质碳素钢材料的加强杠。图6为按照优化方案改制的保险杆。

图5 保险杠优化方案示意图

图6 优化方案改制的保险杠

2.2 优化设计后保险杠模态计算

表2是优化后保险杠前5阶固有频率和振型的计算结果，从表2中可以得出，优化设计将保险杠的第1阶模态频率由94 Hz提高到113 Hz，避免了保险杠在工作过程中发生共振。同时，优化设计改善了保险杠的固有动态特性，保险杠的支撑性能得到提高，刚度明显增强。

表2 优化保险杠前5阶固有频率和振型

3 试验验证

为了验证优化设计对保险杠振动的改善效果，将改制保险杠重新安装在车辆上，再次进行振动测试，并将改进前、后的振幅曲线进行对比分析。图7为保险杠改进前、后各测点的振幅曲线对比。从图7(a)、图7(b)中可以看出，保险杠在5 600 r/min转速段的共振特征被消除，其Z向和X向的振幅下降明显，最大降幅达60%～70%，在整车常用转速段内保险杠振动控制良好，振幅变化也比较平稳，其振动水平得到显著提升。评价人员的主观评价感受是优化后保险杠的振动减轻，振动舒适性优于原状态。优化方案有效地解决了摩托车保险杠的振动剧烈问题，且成本较低，易于实施。

图7 保险杆优化前、后振幅曲线

4 结论

1)摩托车保险杠的第1阶模态频率为94 Hz，该阶模态频率与发动机激励频率相耦合，发生共振，从而导致保险杆的振幅急剧增大。

2)针对保险杠的振动舒适性问题，通过在保险杠左、右两侧分别焊接2根φ18×2的优质碳素钢材料加强杠，提高保险杆的连接刚度，将保险杆的第1阶模态频率由94 Hz提高到113 Hz，避免了保险杠在发动机激励频率下发生共振。

3)经优化设计后，保险杆在5 600 r/min转速段的共振特征被消除，振幅下降达60%～70%，优化方案经济合理、科学有效，保险杆的振动水平有了显著改善。研究结果提供了新的保险杆设计方案，为摩托车保险杆的振动控制与结构优化提供工程决策依据。