基于环形电磁线圈的轮轨增压方案

应之丁 李 艺 桂安登

(同济大学铁道与城市轨道交通研究院，201804，上海∥第一作者，副教授)

列车基础制动力由轮轨间的相互黏着关系产生，提高轮轨间的黏着作用可以有效提高列车设计时速标准。文献[1]研究发现，通过改善轮轨表面清洁、增加轴重等方法可以增大轮轨黏着系数。文献[2]利用MMS-2A型微型计算机控制摩擦磨损试验机进行试验，认为轮轨接触面积和黏着力随着轴重的增加而增大。文献[3]的研究表明，增加轴重负载会导致车轮黏着系数下降以及黏着力上升。

本文根据现有轮轨黏着关系及电磁学原理，提出一种轮轨电磁增压方案。该方案通过电磁线圈磁化车轮，令轮轨间产生较大的垂向电磁吸力，从而达到增加轴重的目的。本文同时设置了内嵌环形线圈励磁模型和外置环形线圈励磁模型，基于Ansoft Maxwell电磁场分析软件分析了两种模型的磁感应强度、垂向电磁吸力等参数。所提方案可以改善列车运行过程中由于轮轨之间黏着力不足而引发的制动力不足问题，为列车轮轨增加黏着力问题提供解决思路。

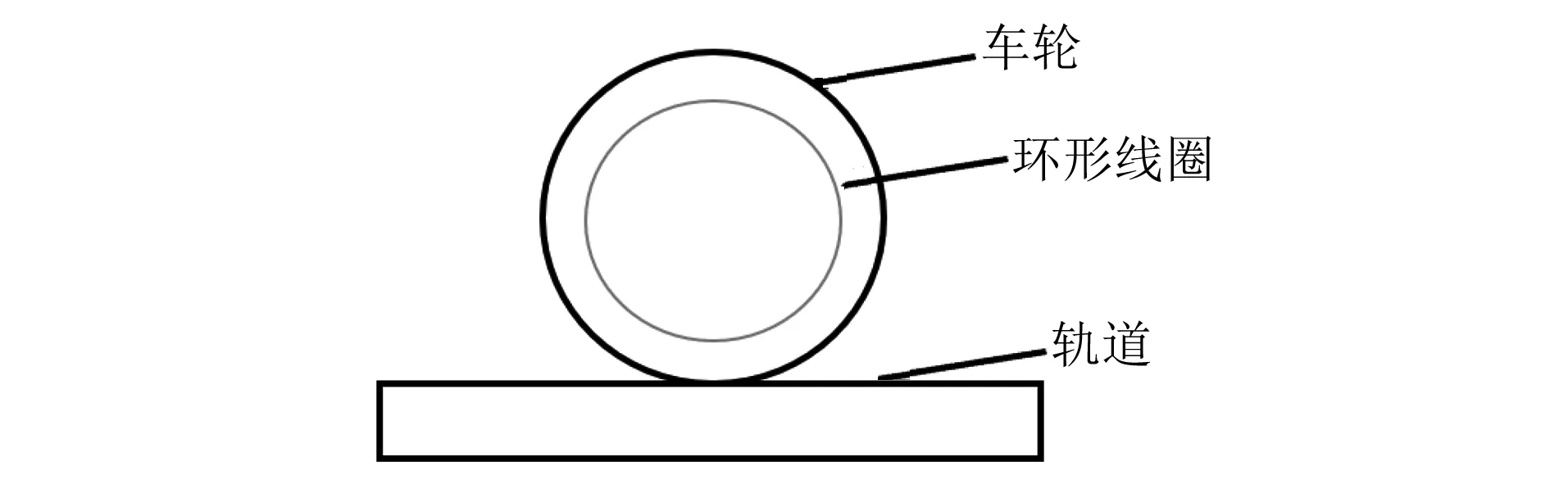
图1 基于车轮结构的增压方案示意图Fig.1 Diagram of pressurization scheme based on wheel structure

1 增压方案中施加电磁力的相关因素分析

基于车轮结构的增压方案示意图如图1所示。图1的基本原理为将环绕车轮布置的励磁线圈和车轮简化为一个巨大的电磁铁，励磁电流输入环形线圈产生磁场磁化车轮，同时对轨道产生电磁吸力，以实现增大轮轨间垂向作用力的目标，即通过电磁作用增加轴重来提高轮轨黏着力。但由于轮轨间的复杂接触关系、线圈尺寸及形式多样等因素的影响，需要通过建立轮轨间的电磁场模型来分析各因素对电磁场形态的影响。

轮轨接触关系示意图如图2所示，可采用经验公式计算电磁吸力。由于轮轨接触面不固定，选取车轮踏面中段与上部轨面接触这一位置进行分析。车辆与轨道在列车运行过程中相互贴合，可忽略轮轨接触面上的空气间隙，分段计算电磁作用吸力。在计算电磁场时，需要对给定区域中的微积分方程进行求解。由于轮轨模型几何结构的复杂性，通过数值计算方法离散求解区域[4]。

图2 轮轨接触关系示意图Fig.2 Diagram of wheel-rail contact relationship

由于只计算垂向电磁作用力，所以采用纵向离散轮轨模型。利用能量法进行推导，考虑到漏磁现象，对于离散模块任一子单元的电磁力FΔS的计算公式为[5]：

(1)

式中：

BΔS——离散单元所处位置的磁感应强度，T；

S——车轮离散模块投射到对应轨道表面的投影面积，m2；

μ0——真空磁导率；

Kf——漏磁系数。

在计算过程中，可将轮轨贴合接触面位置部分视为特殊形式的起重电磁铁来计算[6]，轮轨接触斑励磁下对轨道的电磁吸引力FP为：

(2)

式中：

SP——轮轨接触斑面积，mm2；

I——励磁电流，A；

N——线圈匝数，匝；

B——磁感应强度，T；

δ——集肤深度，mm。

根据经验，通常认为轮轨贴合处接触斑空气隙为0.5 mm。综上所述，总的电磁吸力可以表示为：

2 基于转向架车轮结构的增压模型

根据上述环绕车轮布置线圈的电磁增压原理，选择车轮侧面布置线圈，设置内嵌环形线圈励磁模型和外置环形线圈励磁模型。内嵌环形线圈励磁模型如图3所示。由图3可知，线圈内嵌在车轮轮毂内侧且相对车轮保持固定，励磁线圈通电后可磁化车轮踏面，从而实现对轨道的吸附作用。该方案的优点为：利用车轮内部空间，不影响现有转向架结构；回路磁阻较小，在踏面处可获得一定的磁感应强度。

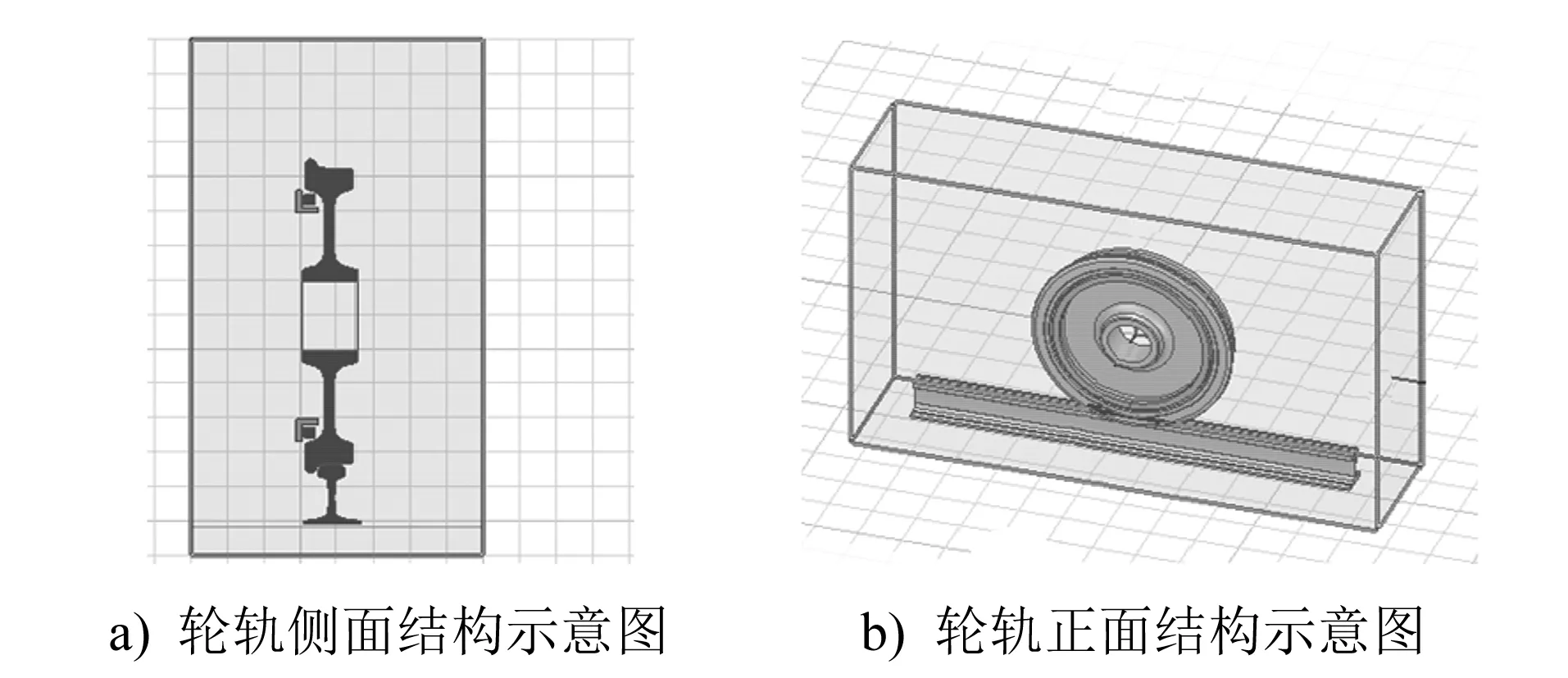
图3 内嵌环形线圈励磁模型Fig.3 Embedded ring coil excitation model

外置环形线圈励磁模型如图4所示。在空间电磁场中，考虑到磁感线回路被约束在强铁磁性材料边界内而不易穿过空气-铁磁性材料交界面的情况，选择将线圈贴近轮轨接触面，在车轮外侧面外置励磁装置。环形线圈通电后构成的磁感线闭合回路A如图4 b)所示。由于回路中磁阻较小，相同电流激励下所获得的磁感应强度更大。在轮轨接触面上，磁感线方向与其法线方向重合，轮轨间电磁吸力的垂向分力最大。

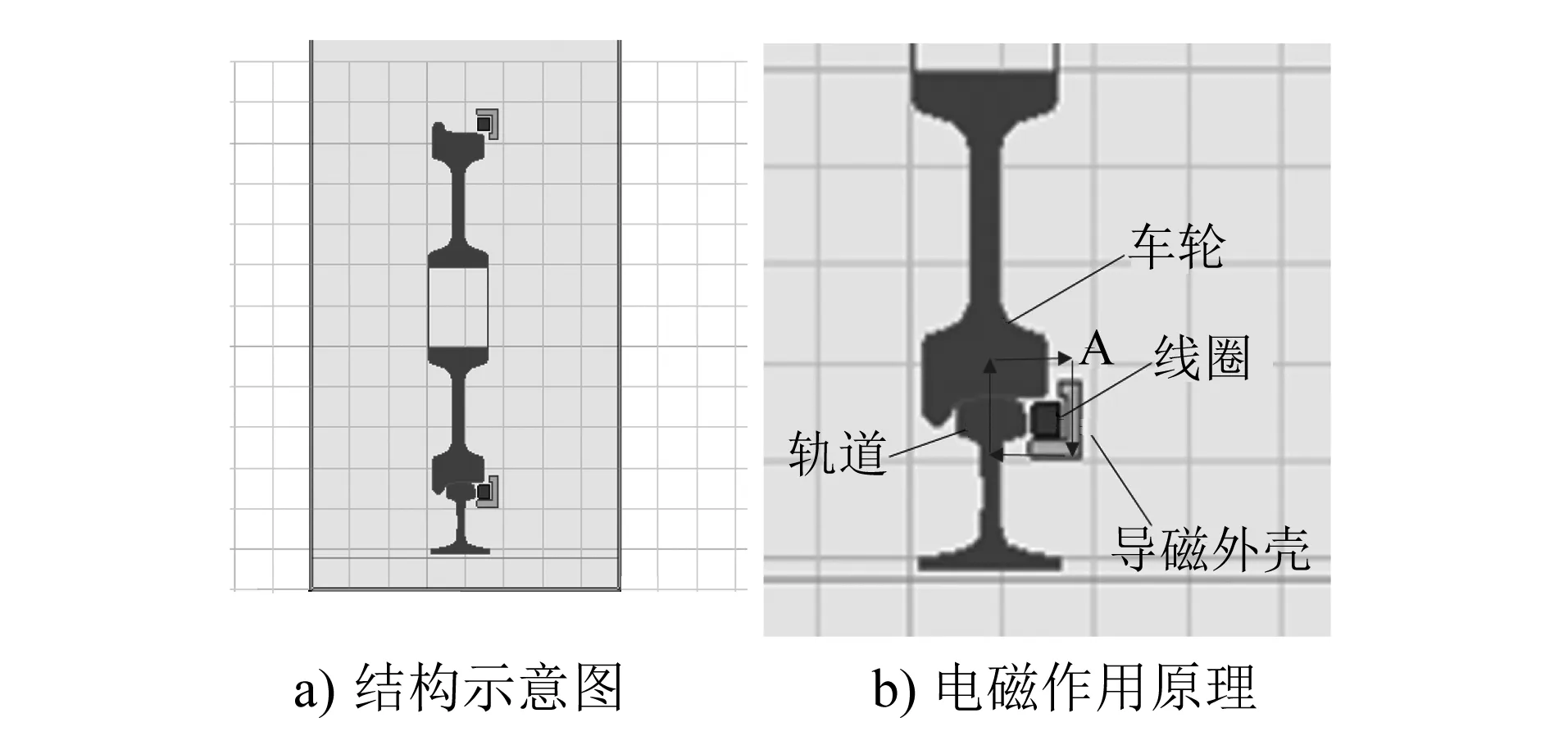
图4 外置环形线圈励磁模型Fig.4 External ring coil excitation model

3 电磁增压模型仿真

基于Ansoft Maxwell电磁场分析软件，根据电磁场原理及实际线路情况向线圈输入恒定直流电激励产生恒稳磁场，计算电磁场在轮轨间隙位置处的电磁吸力。

3.1 内嵌环形线圈励磁模型

静磁场中，对线圈施加10 kAN(安匝数)的直流电激励，计算获得轨道所受垂向电磁吸力为114.87 N。通过软件仿真获得的内嵌环形线圈励磁模型磁感应强度云图如图5所示，其中导磁外壳厚度为20 mm。由图5可知，磁感线主要通过导磁壳体导流构成回路，导磁壳体截面上的磁感应强度达到了1.20 T。由图5 b)可知，该处电磁场畸变突出，磁感应强度最大值达到了0.12 T。由于轮轨间不存在接触，轨面其他部分的磁感应强度只有0.08 T左右。

图5 内嵌环形线圈励磁模型磁感应强度云图

磁场主要集聚在轮毂内侧，由于车轮材料具有强铁磁性，磁感线不易穿透车轮抵达轨道轨面，轮轨间隙位置的磁感应强度较低。选择线圈励磁直流电区间3～15 kAN，以1 kAN为步长，获得轮轨间垂向电磁吸力随着线圈励磁安匝数的变化如图6所示。由图6可知，在提供激励15 kAN的情况下，产生的电磁吸力仍不足300 N。由此可知，内嵌环形线圈励磁模型对轮轨的增压效果不明显，其增加轴重的调节效果不显著。

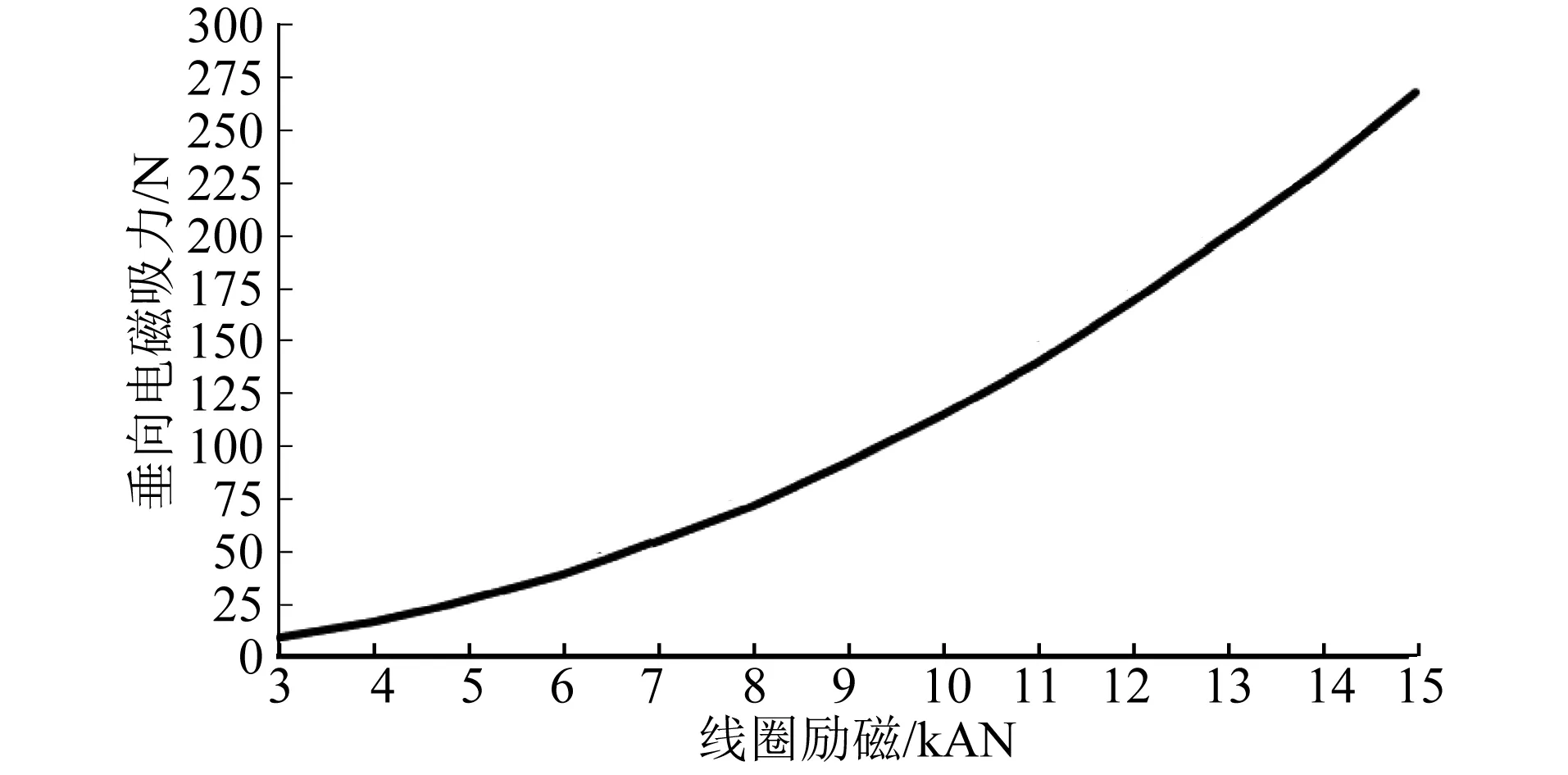
图6 内嵌环形线圈励磁模型中的垂向电磁吸力随线圈励磁安匝数的变化

3.2 外置环形线圈励磁模型

静磁场中，对线圈施加10 kAN的直流电激励，计算获得轨道所受垂向电磁吸力为3 979.80 N，其作用效果约是内嵌环形线圈励磁模型的34倍。通过软件仿真获得的外置环形线圈励磁模型磁感应强度云图如图7所示。磁场在轮轨接触面上的磁感应强度达到了0.90 T，在轨面上的磁感应强度均匀分布且数值在0.80 T左右。相比于内嵌环形线圈励磁模型，外置环形线圈励磁模型可对轮轨接触位置产生更加稳定的励磁作用，轮轨接触面可获得较大的磁感应强度值，且其磁感线垂直于轮轨接触面，即该处可获得最大的垂向电磁吸力，对车轮增压效果明显。

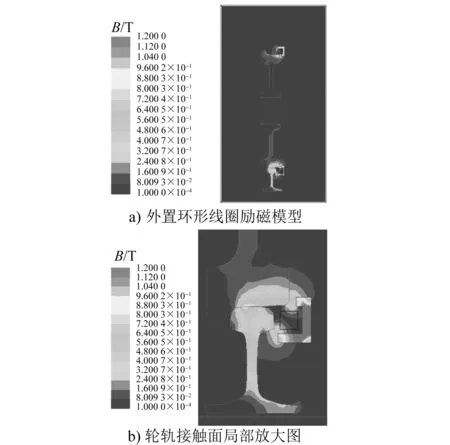
图7 外置环形线圈励磁模型磁感应强度分布

选择线圈励磁直流电区间3～15 kAN，以1 kAN为步长，获得轮轨间垂向电磁吸力随着线圈励磁安匝数的变化如图8所示。由图8可知，垂向电磁吸力与线圈励磁安匝数呈二次函数关系，符合电磁铁电磁吸力简化模型。对于轴重约为21～23 t的车辆，在10 kAN的线圈直流电激励作用下, 所提模型可以增加3.5%左右的轴重，在15 kAN的线圈直流电激励作用下, 所提模型可以获得7.4%的补充轴重，初步满足轮轨增压需求。

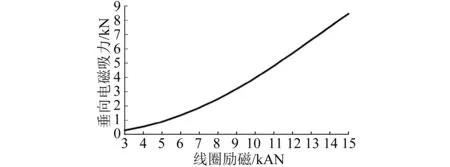
图8 外置环形线圈励磁模型垂向电磁吸力随线圈励磁安匝数的变化

4 结语

本文根据轮轨现有结构及电磁学基本原理提出环形电磁线圈增压方案。利用电磁线圈磁化车轮，使其对轨道产生垂向电磁吸力以增加轴重，进而增大轮轨间的最大制动力。内嵌环形线圈模型充分利用了车轮内部空间且相对车轮保持固定，不影响现有转向架结构。该方案轮轨间隙位置的磁感应强度较低，对轮轨的增压效果不明显，对轴重增加的调节平衡效果不显著。外置环形线圈模型将线圈贴近轮轨接触面的车轮外侧面。相比于内嵌环形线圈模型，外置环形线圈可对轮轨接触位置产生更稳定的励磁作用，轮轨处可获得较大的垂向电磁吸力，对车轮增压效果明显。