隔离桩对软弱地层地铁暗挖隧道侧穿电塔的影响分析
2023-02-12段军朝徐朝阳何凯罡
段军朝 徐朝阳 何凯罡
(1.中建三局基础设施建设投资有限公司,430064,武汉;2.中建三局集团有限公司,430064,武汉∥第一作者,高级工程师)
随着我国各城市地铁线网的不断发展,其建设过程中会不可避免地穿越地面既有建(构)筑物,如输电铁塔等[1-2]。隧道掘进过程中对围岩的扰动会造成既有电塔结构不均匀沉降与倾斜,严重时会导致电塔结构破坏、塔身大幅度倾斜甚至倒塌等情况[3]。为此,众多学者对隧道穿越电塔的施工影响规律开展了相关研究。文献[4]采用 FLAC3D软件研究隧道爆破开挖对地面高压铁塔塔基的沉降及质点振动速度的影响规律,并结合现场实测数据进行了对比分析。文献[5]采用数值模拟与现场实测的方法,研究了重庆轨道交通4号线浅埋隧道开挖对地面高压线铁塔稳定性的影响。文献[6]通过数值方法模拟了盾构隧道穿越高压电塔的施工过程,分析了渣土改良、洞内注浆和地面注浆加固措施对盾构隧道穿越建筑物的影响规律。文献[7]以衢九铁路某隧道工程为背景,通过二维弹塑性有限元模型分析了浅埋隧道CD(中隔壁)法施工对既有高压铁塔的影响,并对有无注浆加固两种方案进行了模拟分析。文献[8]采用FLAC3D软件模拟了某条铁路李家冲隧道侧穿高压电线塔时,围岩注浆前后隧道拱顶沉降和塔基沉降的变化规律,并通过现场实测验证了注浆加固方案的可行性。
已有研究大多针对大断面矿山法隧道或盾构隧道穿越电塔施工,对于中等断面且上覆有较厚黏土地层的矿山法隧道穿越电塔的影响研究较少。鉴于此,本文以成都地铁6号线三期工程某矿山法区间隧道侧穿电塔为例,通过数值模拟的方法对比分析隔离桩加固对隧道侧穿电塔的影响规律,并结合现场实测数据对加固效果进行评价。本文研究可为类似工程施工提供参考和借鉴。
1 工程概况
成都地铁6号线三期工程某隧道区间为双洞单线形式,左线长472.3 m,右线长422.7 m,左线与右线隧道中轴线距离为15.2 m,采用复合式衬砌结构,上下两台阶法开挖。隧道断面为马蹄形,最大开挖高度约为7.0 m,最大宽度为6.6 m,开挖面积约为38.1 m2,为中等断面隧道,隧道埋深为6.4~16.0 m。区间隧道左线侧穿一座35 kV输电线路电塔,电塔高21.6 m,根开为4.3 m,基础埋深为3.0 m,隧道左线外缘与基础竖向净距约为5.2 m,最小水平净距约为3.1 m。侧穿段隧道埋深约为8.2 m,区间隧道所处地层从上至下依次为杂填土、可塑黏土、软塑黏土、强风化泥岩和中风化泥岩地层,其中可塑黏土与软塑黏土厚度达到5.5 m,隧道围岩综合分级为V级。区间隧道与电塔的位置关系如图1所示。
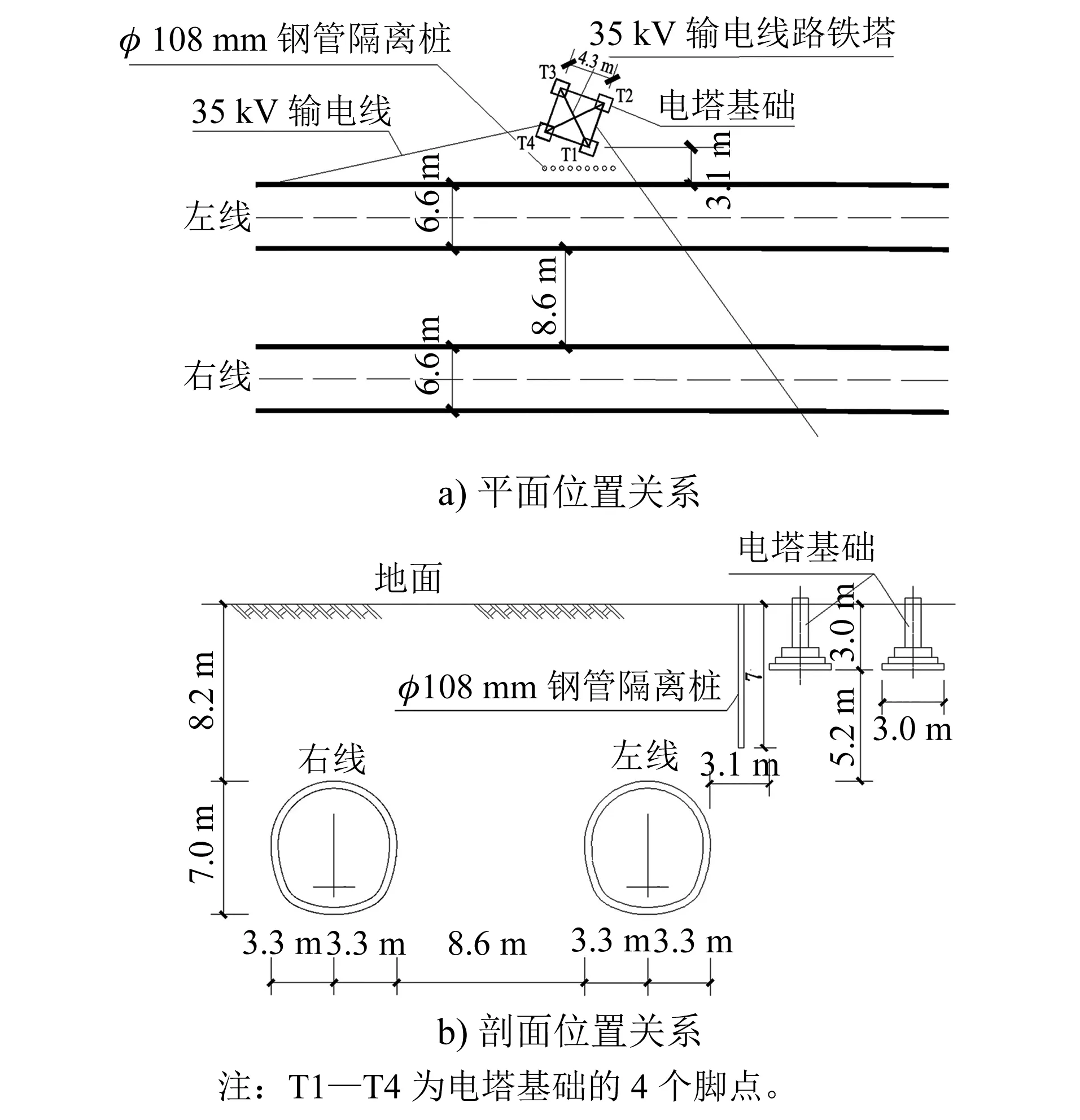
图1 区间隧道与电塔的位置关系Fig.1 Relative location of interval tunnel and pylon
区间隧道在穿越35 kV输电线路电塔前,沿隧道线路方向在电塔基础(以下简称“塔基”)周边施作单排钢管隔离桩。隔离桩距塔基不小于2 m,采用长为7 m的φ108 mm热轧无缝钢花管,管中心间距为0.8 m,打设长度为10 m。钢花管上钻注浆孔,孔径为10~16 mm,孔间距为113 mm,注浆孔呈梅花形布置。
2 数值计算模型及计算工况
2.1 基本假定
数值模拟采用FLAC3D有限差分软件,岩土体采用摩尔-库仑本构模型,隧道初期支护(以下简称“初支”)、电塔结构及基础采用弹性模型。建模时,隧道初支、岩土体及塔基均采用实体单元模拟,电塔采用梁结构单元模拟。根据刚度等效原则,隧道初支采用统一的计算参数。电塔模型忽略风荷载作用,但考虑到电线的牵引力,通过在电塔特定节点处施加集中力的方式进行模拟。计算过程中,为了简化钢管隔离桩注浆加固过程,不考虑浆液的凝固过程。
2.2 三维数值计算模型
选取沿隧道掘进方向66 m,自隧道左、右线边缘向两侧及下部各延伸20 m范围内的岩土体建立三维数值计算模型(满足至少3倍洞径要求),模型总体边界尺寸为60.7 m(横向)×66.0 m(纵向)×35.3 m(竖向)。模型上表面为自由面,底面施加竖向约束,前后和左右边界各施加与之垂直的水平约束。区间隧道电塔三维数值计算模型如图2所示。地层及建构筑物的主要物理力学参数如表1所示。
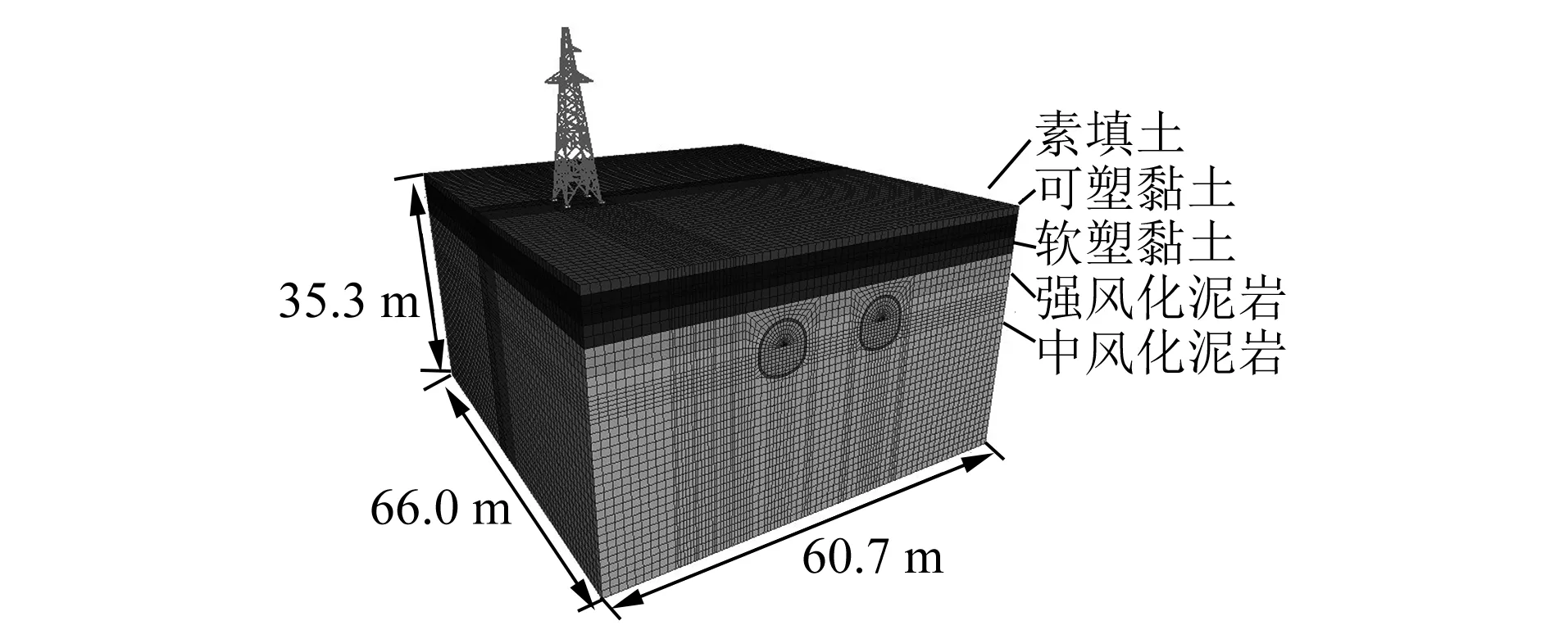
图2 区间隧道电塔三维数值计算模型

表1 地层及建(构)筑物主要物理力学参数
2.3 施工过程模拟及计算工况
在隧道开挖前,首先考虑自重进行初始地应力平衡计算,然后将位移清零作为分析的初始状态。该区间隧道采用上下台阶法施工,上台阶开挖步长为1 m,台阶长度为4 m;下台阶左右交替开挖,一次开挖步长为2 m,且左右两侧错开4 m。根据现场实际施工情况,在上下台阶贯通后进行仰拱开挖。通过FISH语言编写循环结构模拟矿山法开挖过程。开挖循环内容主要包括:① 开挖上台阶土体,施作上台阶初支;② 开挖左侧(或右侧)下台阶土体,施作左侧(或右侧)下台阶初支;③ 隧道上下台阶贯通后,逐步开挖仰拱土体,并逐步施作仰拱初支。
本次数值计算模拟采用右线在前、左线在后,两条隧道平行开挖的方式,左、右线开挖面前后错开6 m。本文共计算了两种工况:未采取加固措施;采取钢管隔离桩注浆加固措施。
3 计算结果分析
3.1 地面位移分析
左、右线隧道开挖完成时,两种工况下电塔中心断面处(T1与T3连线中点位置)地面位移变化曲线如图3所示。由图3可知,未采取加固措施时,双线隧道贯通时地面沉降槽呈W形分布,地面位移峰值出现在左、右线隧道拱顶位置处,分别为13.30 mm与13.20 mm,均在监测预警值范围内。采取加固措施后的地面沉降槽与未加固时类似,差异主要出现在加固处两侧约6.00 m范围内,隔离桩加固使地面沉降明显减小,且减小量的最大值出现在隔离桩位置,为4.57 mm,相比于未加固时的9.75 mm,降低了约46.9%。
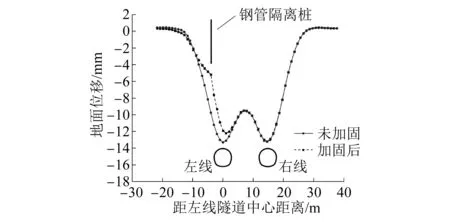
图3 双线隧道贯通后地面位移变化曲线
3.2 塔基竖向位移与倾斜分析
选取电塔4个脚点(其具体位置见图1 a)),分析矿山法隧道掘进时的电塔位移变化规律。两种工况下, T1—T4脚点随隧道开挖的塔基竖向位移变化曲线如图4所示。
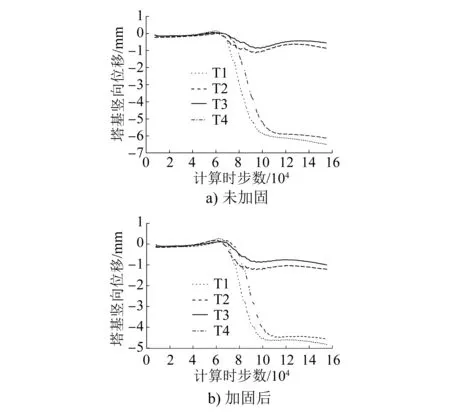
图4 两种工况下的塔基竖向位移变化曲线
由图4可知,随着隧道不断掘进,塔基竖向位移变化大致分为3个阶段:① 基本保持不变,后出现略微隆起;② 出现明显沉降,其变化速率表现出先快再稳定最后变慢的特点;③ 塔基沉降变化趋于稳定,数值变化较小。通过计算可以发现,第1阶段与第2阶段的分界点出现在右线隧道距离电塔8 m左右的位置,第2阶段与第3阶段的分界点大致出现在左线掌子面通过电塔处。由此可以说明,在矿山法隧道侧穿电塔时,当隧道掌子面进入电塔一侧8 m范围后,塔基开始出现明显沉降,直至隧道掌子面穿越电塔后开始趋于稳定。当隧道掌子面距离电塔超过8 m时,隧道掘进对塔基竖向位移的影响较小,可以忽略不计。
两种工况下的塔基最终竖向位移如图5所示。由图5可知,塔基沉降大小关系表现为T1沉降量>T4沉降量>T2沉降量>T3沉降量,与T1—T4脚点距左线隧道距离远近关系一致,即距离隧道越近,塔基沉降越大,但两者之间并非呈线性关系。此外,从图5中还可以发现,采取钢管隔离桩加固对于塔基的沉降变化具有明显的影响。两种工况下,塔基的沉降变化规律基本一致,但加固后距离隧道较近一侧塔基的最终沉降明显降低,而较远一侧的塔基最终沉降略微变大。例如,采取加固措施后,相比于未加固时T1处的最终竖向位移(6.50 mm),加固后T1处的最终竖向位移为4.82 mm,降低了1.68 mm;相比于未加固时T3处的最终竖向位移(0.55 mm),加固后T3处的最终竖向位移为0.99 mm,仅增加了0.44 mm。

图5 两种工况下的塔基最终竖向位移
除电塔每个脚点处的基础沉降变化规律外,塔基的不均匀沉降也是结构安全性分析的重要指标之一。根据图4中各脚点处基础沉降的变化规律可以看出,T1与T2脚点处的不均匀沉降差异较大,故选取这两个脚点处的基础沉降数据,绘制出两种工况下的塔基竖向位移差变化曲线,如图6所示。由图6可知,随着隧道掘进的变化,塔基竖向位移差也大致分为3个阶段:① 基本保持不变;② 竖向位移差明显变大,其变化速率表现出先加快然后稳定最后变慢的特点;③ 竖向位移差变化趋于稳定。采取钢管隔离桩加固对于塔基的竖向位移差影响显著,相比于未加固时的5.63 mm,加固后的塔基最终竖向位移差为3.62 mm,减少了约35.7%。

图6 两种工况下的塔基竖向位移差变化曲线
由于塔基的不均匀沉降,电塔发生了倾斜。 DL/T 5219—2014《架空输电线路基础设计技术规定》中5.3.1条规定,塔基的最大倾斜率d应满足地基变形允许值的要求,如表2所示。电塔倾斜率是指基础倾斜方向两端点的沉降差与其距离的比值。本工程中,T1与T2脚点处的不均匀沉降差异最大,两者之间的距离为4.3 m,经过计算可获得电塔的倾斜率变化曲线,如图7所示。由图7可知,采取钢管隔离桩加固对于电塔倾斜率的影响显著,相比于未加固时的0.001 31,加固后的电塔最终倾斜率为0.000 84,减少了约35.8%,满足相关规范要求。

表2 地基变形允许值Tab.2 Allowable deformation value of foundation
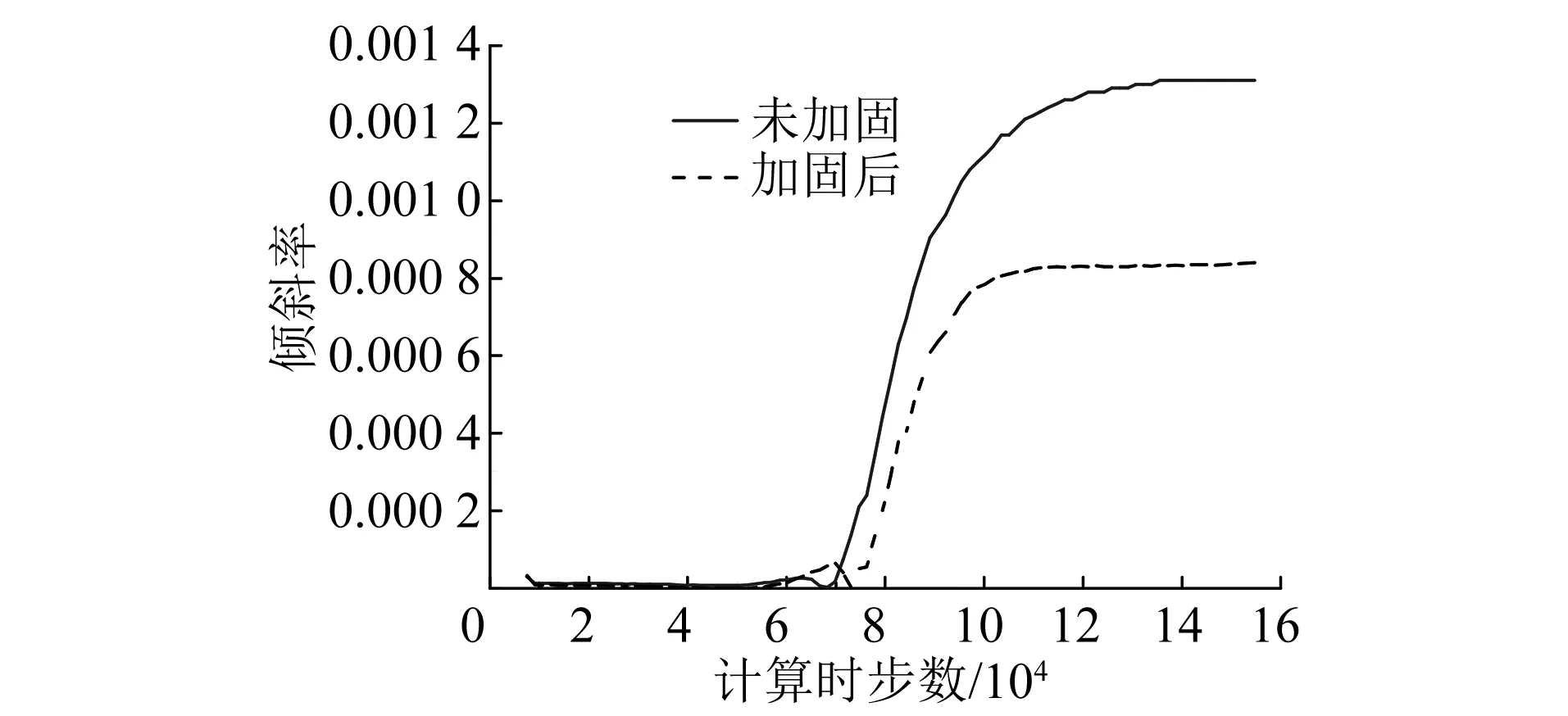
图7 两种工况下的电塔倾斜率变化曲线
3.3 电塔结构内力分析
3.3.1 电塔应力分布特点
为进一步研究矿山法隧道侧穿施工对电塔结构受力的影响,对隧道施工前和隧道贯通后两个时刻下的电塔结构内力进行分析。两种工况下,隧道开挖前与贯通后的电塔结构轴应力云图如图8和图9所示。由图8和图9可知,两种工况下,隧道开挖前与贯通后电塔主材均为受压状态,自上而下所受的轴应力越来越大,且左侧主材的压应力小于右侧主材的压应力。而斜材、隔材和辅材有的受拉,有的受压。电塔的最大压应力均出现在塔腿主材处,而最大拉应力则出现在塔腿附近的斜材或辅材处。
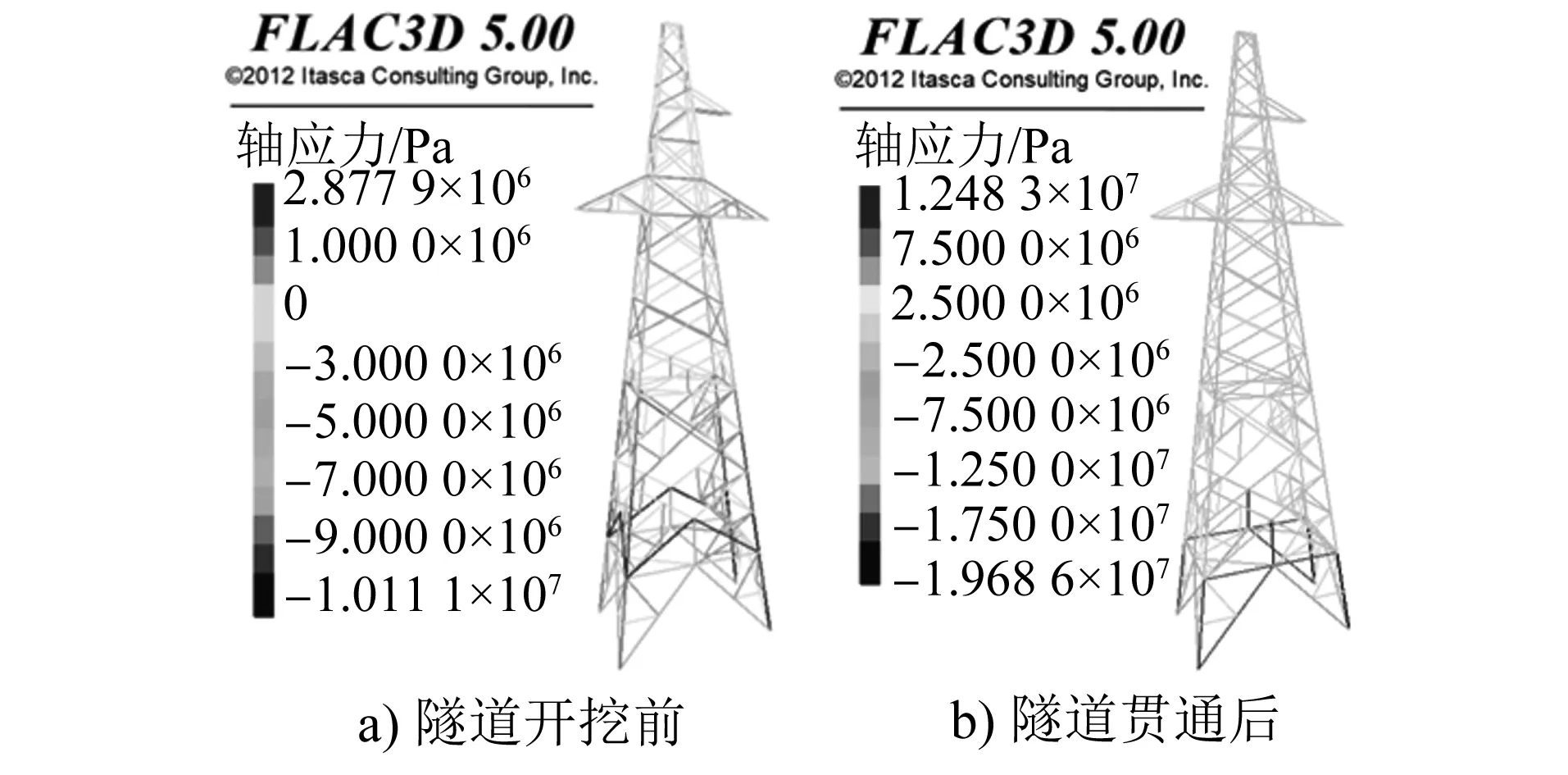
图8 未加固时的电塔结构轴应力云图截图Fig.8 Screenshot of pylon structure axial stress nephogram without reinforcement
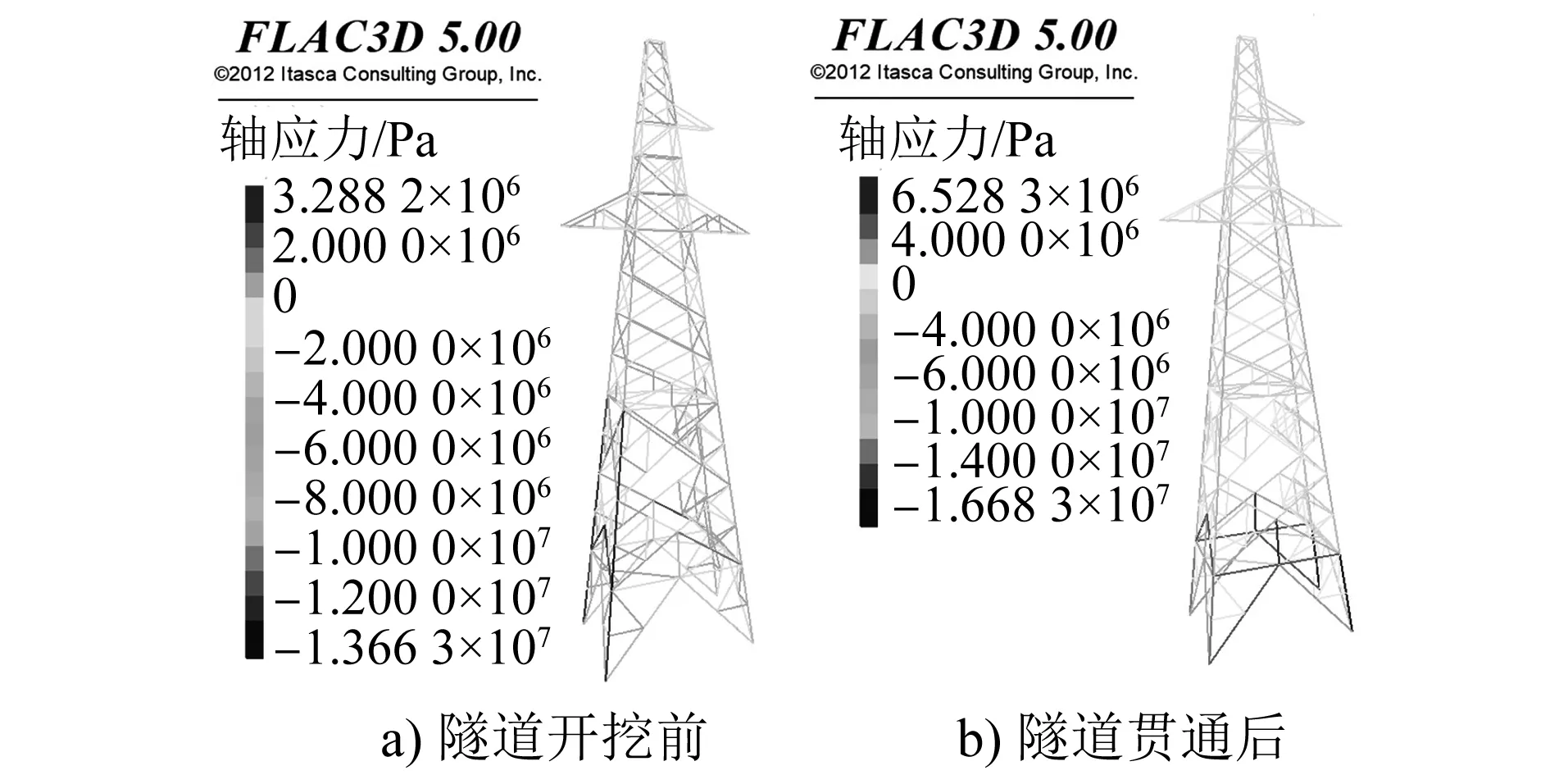
图9 加固后的电塔结构轴应力云图截图
隧道贯通后,两种工况下的电塔结构内力均有所增大。同一工况下,最大拉应力的增幅明显大于最大压应力。例如未加固时,两者的增幅分别为332.0%和94.8%。加固后,在隧道开挖前,电塔结构的最大压应力和最大拉应力分别增长了35.1%和14.0%;在隧道贯通后,电塔结构的最大压应力和最大拉应力显著降低,幅度分别为15.3%和47.7%。
3.3.2 塔腿应力分析
经上述分析可知,电塔的塔头、塔身和塔腿三部分中以塔腿的应力最大,其中又以塔腿的主材和斜材受力最大,故单独分析塔腿主材与斜材的受力情况。每个脚点处共有1个主材和2个斜材,将两种工况及隧道开挖前与贯通后塔腿主材、斜材的轴应力及其变化量分别进行统计,如表3和表4所示。
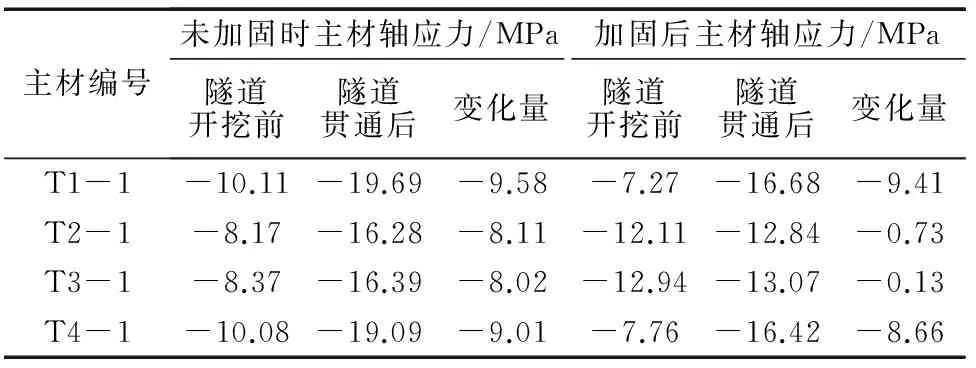
表3 塔腿主材的轴应力及其增变化量
由表3可知,所有情况下,塔腿主材均为受压状态。未采取加固措施时,塔腿主材在隧道开挖前后均是靠近左线隧道一侧的压应力较大,且同一侧的主材所受的压应力相差较小。采取加固措施后,在隧道开挖前,塔腿主材远离隧道一侧受力较大;在隧道贯通后,塔腿主材靠近隧道一侧受力较大。未采取加固措施时,每个塔腿主材的应力变化量相差不大,其数值基本为8.0~9.5 MPa;而采取加固措施后,靠近隧道一侧的塔腿主材应力变化量变化较大,为8.6~9.4 MPa,远离隧道一侧的塔腿主材应力变化量较小,在1.0 MPa以内。由此说明,采取加固措施对于远离隧道一侧的塔腿应力变化有显著影响,而对靠近隧道一侧的塔腿应力影响较小。

表4 塔腿斜材的轴应力及其变化量
由表4可知:在隧道开挖前,无论是否采取加固措施,塔腿斜材均为受压状态;在隧道贯通后,塔腿斜材部分为受压状态,部分为受拉状态。总体而言,同一工况下,相比于隧道开挖前,隧道贯通后不同位置处的塔腿斜材轴应力变化差异较大,其变化幅值为0.37~9.00 MPa。采取加固措施后,每个塔腿斜材的轴应力变化量均有所下降,且降幅大小不一,最大降幅能达到91.4%,而最小降幅仅有10.5%。
综上所述,采取加固措施对于远离隧道一侧的塔腿主材轴应力变化影响显著,也能有效降低塔腿斜材的轴应力变化幅值,最大降幅达到91.4%。可见隔离桩加固对于电塔结构的内力变化影响显著。
4 加固实施效果评价
经上述模拟分析,现场决定采用钢管隔离柱加固方案,严格控制现场施工过程,最终顺利完成暗挖隧道侧穿电塔施工。施工中对地面位移、塔基竖向位移、洞内拱顶沉降和水平收敛等进行了系统监测,现场监测数据均在可控范围内。为了进一步验证计算结果的可靠性,绘制地面累计位移曲线,地面竖向位移计算值与监测值对比如图10所示。电塔塔基累计沉降计算值与监测值对比如表5所示。
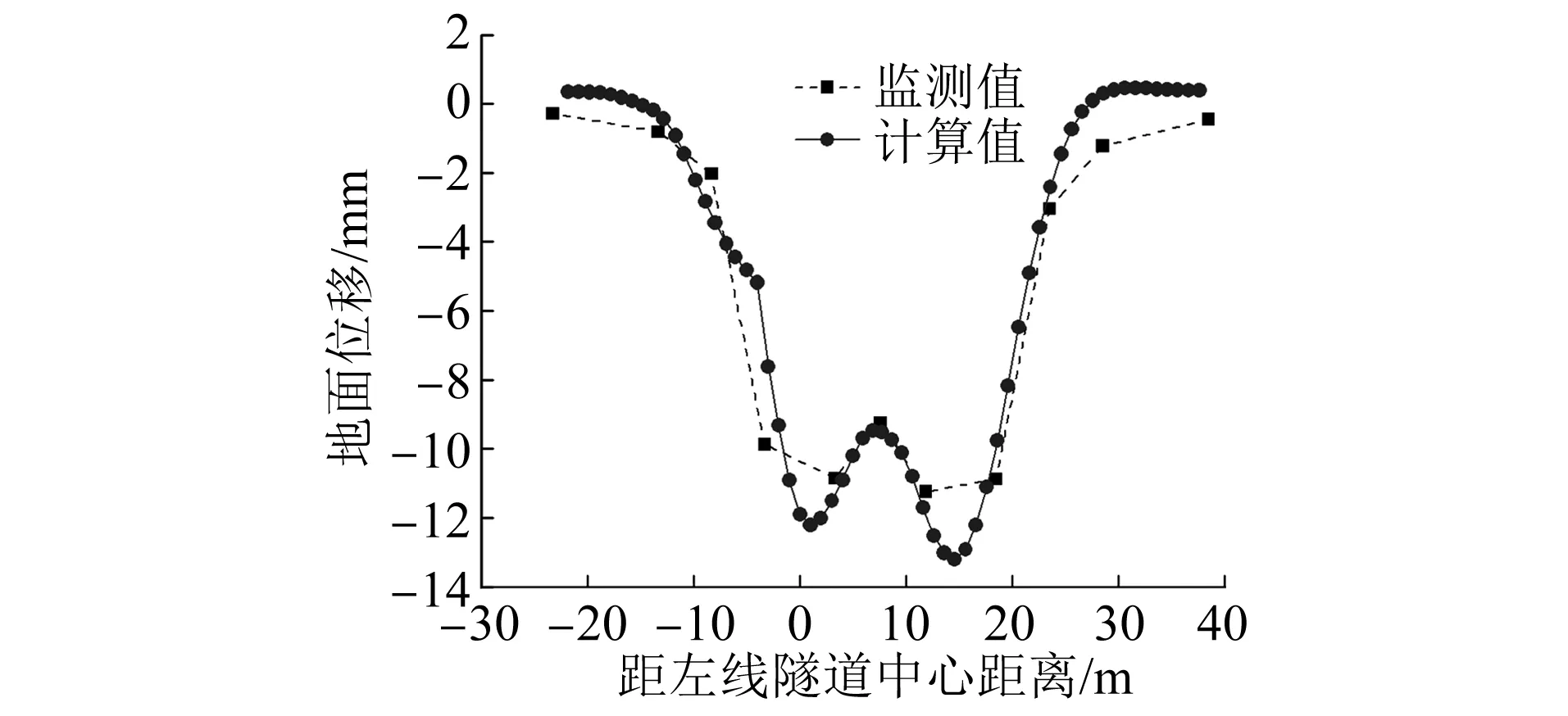
图10 地面竖向位移计算值与监测值对比

表5 电塔塔基累计沉降计算值与监测值对比
由图10及表5可以看出,监测值与计算值相差较小,考虑到计算误差等因素,可以认为两者基本吻合,验证了数值计算模拟的可靠性。同时,上述分析也表明了,采用钢管隔离柱对软弱地层进行加固可以保障暗挖隧道侧穿电塔的施工安全,获得较好的加固效果。
5 结论
1) 隧道穿越完成后,地面沉降槽呈W型分布,采取钢管隔离桩加固后,加固区左右两侧6.00 m范围内的地面沉降显著降低,其他区域地表位移变化较小。
2) 隧道穿越完成后,靠近隧道一侧的塔基沉降较大,远离隧道一侧的塔基沉降较小,由此会造成塔基的不均匀沉降与倾斜。采取钢管隔离桩加固能够显著降低电塔倾斜及靠近隧道一侧的塔基竖向位移,而远离隧道一侧的塔基竖向位移略微增大。
3) 隧道穿越过程中,电塔塔腿附近受力较大,其中塔腿主材受到的压应力最大,塔腿附近斜材或辅材受到的拉应力最大。整体而言,钢管隔离桩加固后,电塔结构的内力变化显著降低,且隧道贯通后电塔塔腿处的内力明显下降,对保障电塔结构的安全性与稳定性起到了积极作用。
