膨胀土浸水前后单桩p-y曲线研究
2023-02-12杨迪,江杰,侯凯文
杨 迪,江 杰,侯 凯 文
(1.中铁建设集团南方工程有限公司,广东 广州 511400; 2.广西大学 土木建筑工程学院,广西 南宁 530004; 3.广西大学 工程防灾与结构安全教育部重点试验室,广西 南宁 530004; 4.广西大学 广西防灾减灾与工程安全重点试验室,广西 南宁 530004)
0 引 言
膨胀土是一种对水分极其敏感的特殊黏性土,遍布全球六大洲共计40多个国家,在中国20余个省、市、自治区均有不同范围的分布。随着城市化进程的推进,越来越多的建(构)筑物建造在膨胀土地基中,根据各地资料和有关论著记载,中国每年因膨胀土造成的经济损失超过150亿美元[1]。为降低膨胀土涨缩特性对上部结构的影响,一般建议采用桩基础[2]。桥梁工程的桩基础常常会承受水平荷载,然而,目前膨胀土地基中水平受荷桩的设计只是采用一些经验方法,还存在很多尚需解决的问题,主要表现在:① GB 50112-2013《膨胀土地区建筑技术规范》[3]未给出膨胀土地区桩基水平承载力的计算方法;② 现有规范如JTS 167-4-2012《港口工程桩基规范》[4]虽然给出了黏性土中水平受荷桩的p-y曲线,但采用该曲线设计的浸水后膨胀土地基中的桩基础是不安全的[5]。因此开展膨胀土地区水平受荷桩的研究十分必要。
目前,国内外学者主要针对膨胀土地区的竖向受荷桩和受扭桩进行研究[6-10],对于水平受荷桩,李紫晔[11]和夏炎等[12]研究了膨胀土中抗滑桩的变形受力情况,提出一种与土工膜结合的抗滑桩,并通过工程实例验证了可行性,提供了一种对膨胀土滑坡治理的新思路和新方法。在膨胀土地区基坑围护桩方面,梁作显[13]和纪智超[14]考虑了膨胀土浸水膨胀的影响,采用有限元软件模拟的方法对围护桩的设计参数进行优化。但上述研究主要是基于抗滑桩和支护桩等被动桩来开展,针对主动桩的研究相对匮乏。对于水平主动受荷桩,p-y曲线法是最常用的方法。确定了地面以下各深度的p-y曲线后,采用无量纲迭代法或有限差分法就可以求得桩身的变形和内力。国内外学者针对p-y曲线也做了大量的研究。朱斌等[15]针对粉砂土和砂土地基中的桩基开展了一系列模型试验。丁蓬莱等[16]通过理论分析,得到水平地震作用下桩侧土抗力理论解。李雨润等[17]通过数值分析软件,对砂土和黏土中p-y单元对桩基动力特性的影响进行分析。Su等[18-19]则通过理论分析,考虑非线性桩土相互作用提出了砂土中的桩基p-y曲线。Li等[20]和Yuan等[21]分别针对液化土和层状黏土也开展了相应的试验和理论研究,并认为三次样条法是求解层状土中水平荷载桩响应的首选方法。
从以上研究成果可以看出,水平受荷桩p-y曲线的研究主要是基于黏土或砂土等土质情况,涉及膨胀土地基中的水平桩基研究较少,而且大部分针对支护桩等被动桩来开展研究,对膨胀土浸水过程中的水平单桩的变形和承载力特性的变化规律了解非常有限。现有研究发现浸水后的膨胀土p-y曲线具有明显的应变软化特点[22],采用黏性土p-y曲线设计浸水的膨胀土桩基是不安全的。因此本文通过室内模型试验,探究了浸水前后的膨胀土地区水平受荷单桩的受力、位移及桩身弯矩的变化规律,并建立了p-y曲线理论表达式,为膨胀土地基中水平受荷桩的设计奠定了基础。
1 模型试验
1.1 试验及装置
试验装置兼具浸失水和水平加载功能,主要由模型箱、加载装置和浸水系统组成。模型箱的尺寸为1 000 mm×1 000 mm×1 000 mm,采用厚度为4 mm的钢板焊接而成。加载系统由角钢和铁棒焊接而成,在铁棒上悬吊一个滑轮,通过调节悬挂高度保证加载方向水平,钢绞线穿过滑轮一端连接桩头,另一端悬挂铁挂篮进行分级加载。
浸水系统由水桶、模型箱底部砂石层和浸水管组成,如图1所示。模型箱底部填埋厚为250 mm的砂石层,从底部往上分别为砾石、粗砂和细砂。膨胀土中设置若干直径为16 mm的PVC浸水管,在浸水管上交叉设置4列出水孔并用土工布包裹,防止膨胀土堵塞出水孔,试验时将浸水管底部插入模型箱底部砂石层150 mm,利用水管将水桶和模型箱底部连接,对水桶加水,利用虹吸原理保持水平面与土表面高度一致,以实现膨胀土的完全浸水膨胀。
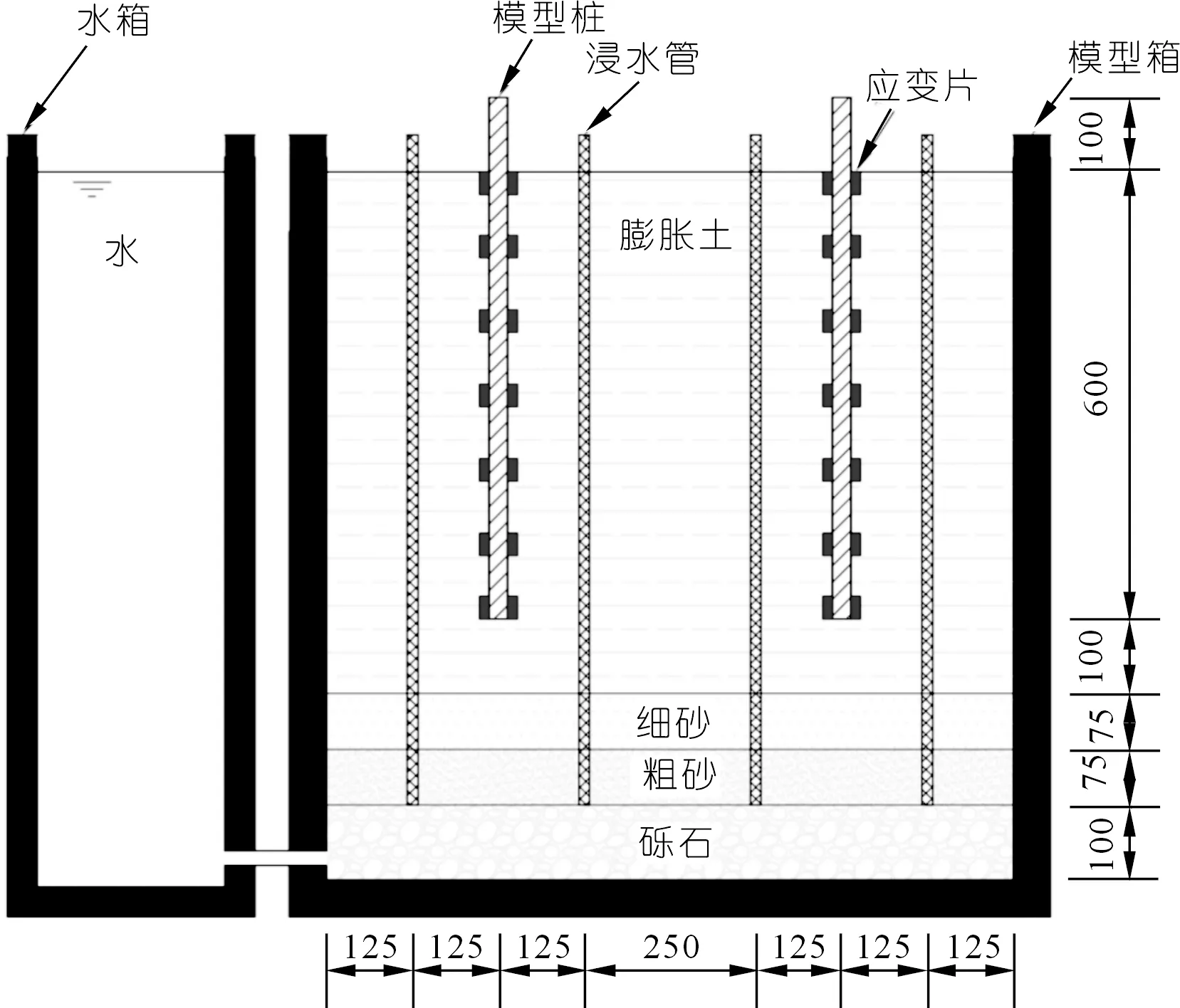
图1 浸水系统示意(尺寸单位:mm)Fig.1 Immersion system schematic
1.2 试验用土
试验土样为广西膨胀土,自由膨胀率为65.5%,根据国家标准GB 50112-2013《膨胀土地区建筑技术规范》[3],属于中等膨胀土,其液限为64.0%,塑限为32.0%,天然含水量为18%,干密度为1.45 g/cm3。土样采用人工夯实的方法分层填筑,控制每层夯实后的厚度为100 mm,填土总高度为700 mm,浸水前后的物理参数如表1所列。

表1 浸水前后的膨胀土参数
1.3 模型桩
根据林海等[23]对水平受荷桩1g下变形特性的相似分析,确定模型与原型各物理量之间的相似常数。根据管桩的尺寸,同时考虑到模型箱的大小以及边界效应的限制,本次试验中取原型桩长50 m,模型桩与原型的相似系数λl取0.012,模型桩长600 mm。原型桩为钢管桩,弹性模量为210 GPa,模型桩为铝合金管桩,弹性模量为69.5 GPa,因此λl=0.33。计算模型桩壁厚使抗弯刚度满足相似比,本文采用文献[23]的方法,可得:
(1)
(2)
式中:EI为抗弯刚度,l为桩长,D和d分别为桩的外径和内径,下标m代表模型桩,无下标代表原型桩。根据式(3)计算:
(3)
模型桩:长lm=0.6 m,外径Dm=0.025 m,结合公式(1) ~(3) 计算得到dm=0.021 m,即模型桩壁厚为2 mm。
模型桩参数如下:桩径0.025 m、壁厚0.002 m、桩长0.6 m、弹性模量70 GPa。为了量测桩身应变值,沿桩身内侧粘贴应变片,应变片布置为上密下疏,粘贴位置如图2所示。将模型桩对半剖开,在桩身内侧标记应变片粘贴位置,并用砂布进行打磨,用胶水将应变片粘贴至标记处。在应变片及其接线端处涂抹环氧树脂进行防水,桩端采用尼龙塞封底,采用环氧树脂粘贴固剖开的模型桩,静置24 h,确保环氧树脂完全凝固。

图2 应变片粘贴位置Fig.2 Strain gauge attachment position
1.4 试验及测量方案
由于膨胀土浸水后强度下降明显,表现出明显的膨胀性,从而影响桩基的工作性状。本次试验方案共分为2组,分别测试水平受荷单桩浸水前后的水平极限承载力。采用自主研制的水平加载系统(见图3),对浸水前后的模型桩进行分级加载试验,建立模型桩的p-y曲线,从而确定模型桩的水平极限承载力。加载过程中,利用TST3822EN静态应变测试仪自动采集桩身应变,在桩顶加载点处及土表处安装2个百分表用以测量桩顶水平位移,桩顶和铁挂篮之间设置一力传感器,用来记录加载级数数据。
采用在铁挂篮添加重物的方式对模型桩进行水平分级加载,并记录每级加载的荷载大小和桩顶水平位移。当每级加载的桩身应变值和位移量稳定时,进行下一级的加载;当某级加载中位移量急剧增加时,则停止加载。

图3 加载装置实物Fig.3 Physical drawing of loading device
2 试验结果
2.1 土抗力
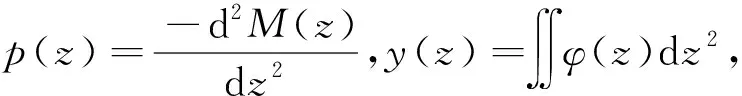
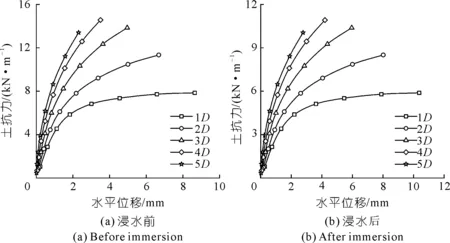
图4 浸水前后不同深度的p-y曲线Fig.4 The p-y curves of different depths before and after immersion
2.2 水平位移
图5为浸水前后不同荷载下桩身水平位移-深度曲线。由图可知,浸水前后桩身水平位移的中性点分别位于桩身0.21 m(8D)和0.25 m(10D)位置(D为桩的直径),浸水后的中性点略低于浸水前;同一荷载作用下,浸水后的桩侧土抗力最大值则略有降低。造成以上结果的原因如下:① 膨胀土浸水后隆起使桩发生了上升,而桩的上升高度低于膨胀土的隆起高度[8];② 如前文所述膨胀土浸水后发生了软化,导致土体刚度降低,从而使中性点下移。
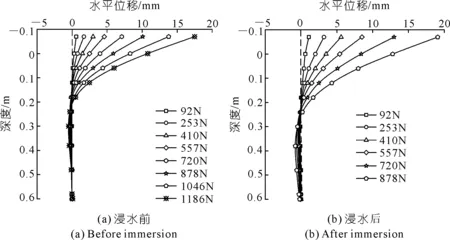
图5 浸水前后不同荷载下桩身水平位移-深度曲线Fig.5 Horizontal displacement-depth curves of pile under different loads before and after immersion
2.3 桩身弯矩
图6为不同荷载水平下桩身弯矩-深度曲线。由图6(a)可知,浸水前,桩身弯矩自桩顶往下先逐渐增长随后再减小,在桩端2D~7D范围出现负弯矩,符合水平受荷桩的荷载传递规律。由图6(b)可知,浸水后,桩身弯矩沿深度的分布呈现两头小中间大的模式,由于测量点不够密集,出现了测量误差,距桩端4D范围的弯矩接近于0,并未出现负弯矩。
浸水前后桩身弯矩最大值位置分别为埋深0.10 m(4D)和0.12 m(4.8D)附近,浸水后的桩身弯矩最大值位置降低,且桩身弯矩较浸水前的有所增大。究其原因,当桩顶荷载不变时,浅层土体浸水后软化,刚度降低,极限土抗力减小,而桩身水平位移增大,弯矩最大值位置下移。
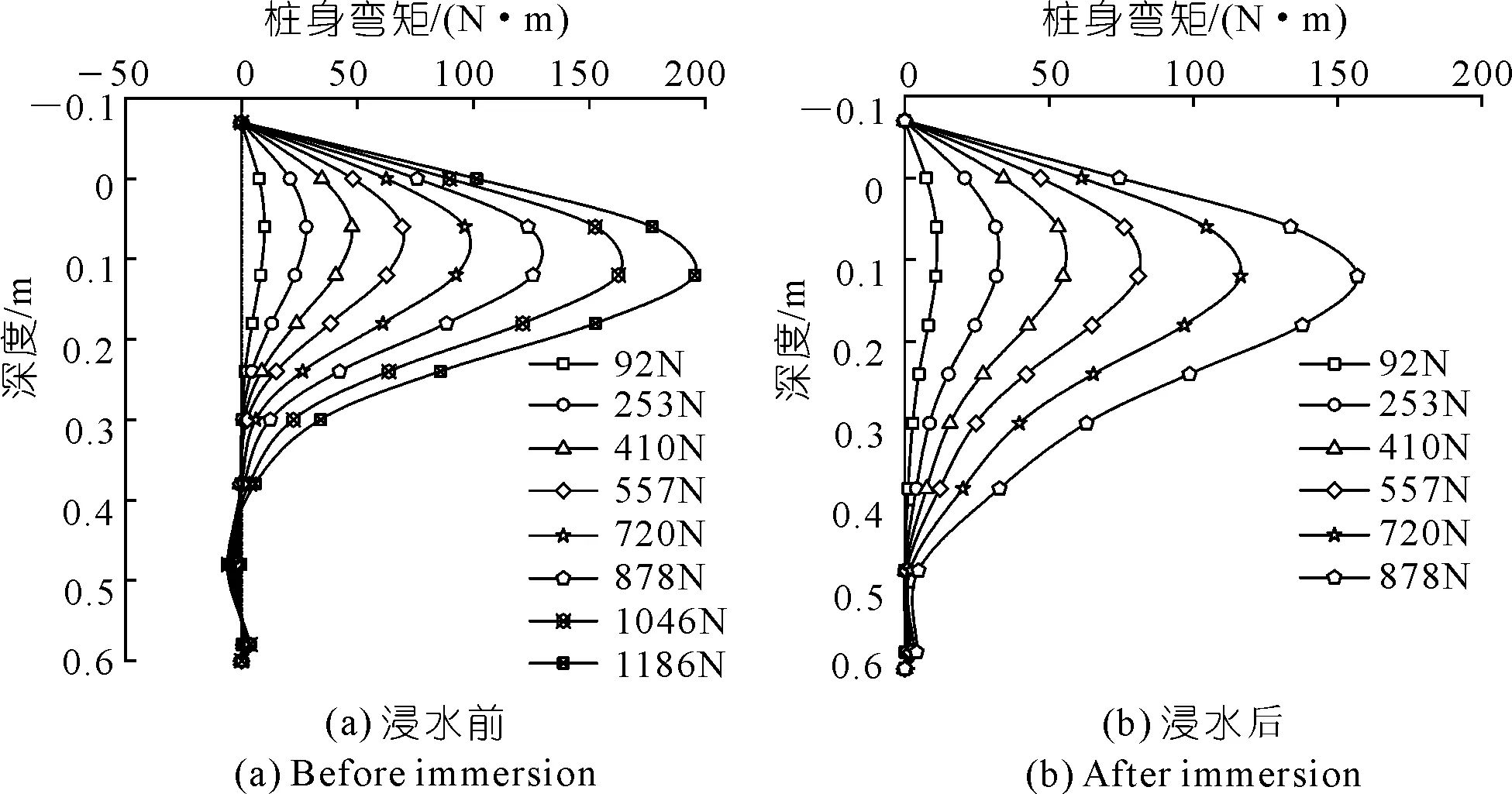
图6 浸水前后不同荷载水平下桩身弯矩-深度曲线Fig.6 Moment-depth curves of pile under different loads before and after immersion
3 理论p-y曲线
3.1 p-y曲线形式
现有已确定的、较权威的p-y曲线理论公式有很多,其中具有代表性的有Matlock方法、Reese方法、Sullivn方法、河海大学新统一法以及同济大学新统一法。上述各种方法中p-y曲线计算公式的形式主要有幂函数和双曲线函数。笔者分别采用以上两种函数形式对实测p-y曲线进行拟合,通过比较发现采用双曲线形式能够很好地拟合浸水后的实测p-y曲线。
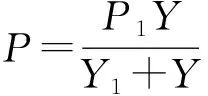
(4)
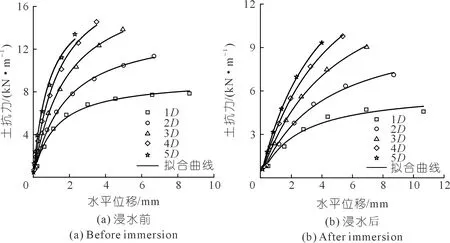
图7 不同深度处膨胀土浸水前后单桩实测p-y曲线Fig.7 Measured p-y curve of singles pile before and after immersion under different depths
3.2 参数的确定
要完全确定p-y曲线的理论计算公式,首先需要求解出式(4)中的未知参数B,Pu和Y50。在图4实测p-y曲线中,不同深度处的土抗力均未达到极限土抗力值。因此,膨胀土浸水前后的实测p-y曲线均可采用双曲线表达式进行拟合,将拟合所得参数Pu和Y50的数值总结如表2所列。参考河海大学新统一法的双曲线形式,有如下关系式:
(5)
式中:K,A为待定参数;Cu为三轴不排水抗剪切强度;D为模型桩直径,取0.025 m;ε50为三轴不排水抗剪强度Cu/2处的应变值。
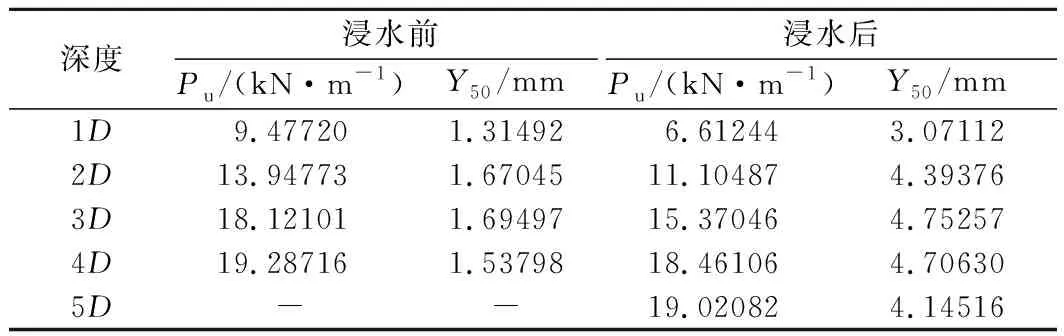
表2 膨胀土浸水前后实测p-y曲线拟合参数
3.2.1Y50的确定
根据公式Y50=Aε50D可知,若确定了参数A的值,则Y50的计算公式即可确定。要确定参数A首先需要单独观察表示各含水量条件下Y50的取值情况。显然表3中同一含水量条件下的Y50取值大小相差不大,因此先对Y50取平均值,然后再利用公式反推参数A,参数A的计算过程与结果如表3所列。将计算结果代入公式Y50=Aε50D,即可确定Y50的表达式。
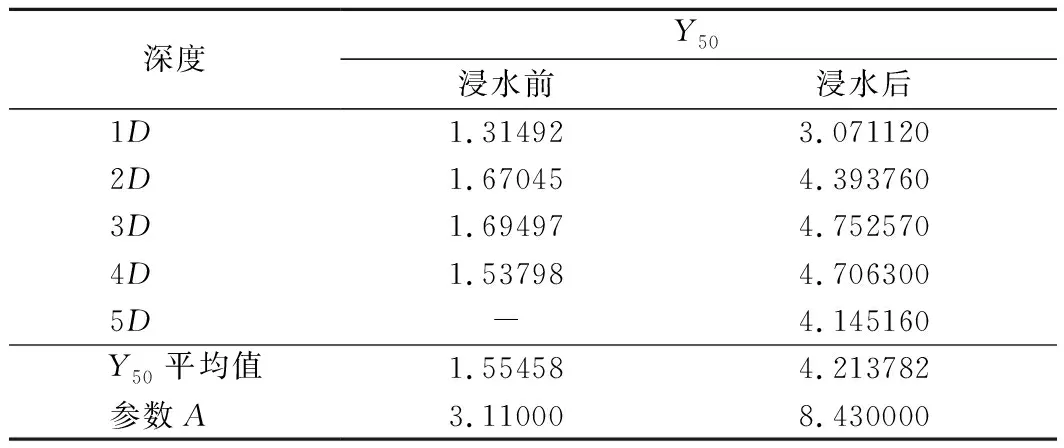
表3 参数A的计算过程
3.2.2Pu的确定
同样地,根据公式Pu=KACuD可知,确定Pu计算式的前提条件是求出参数A和参数K。上文已经求出来了参数A的计算公式,因此只需确定参数K即可完全确定Pu,而参数K可通过表达式Pu=KACuD反算得出。将参数K的计算结果,列于表4。
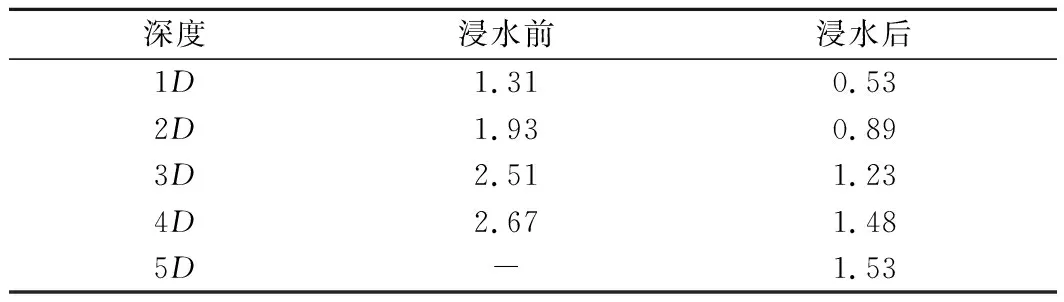
表4 参数K的计算结果
为了便于探究参数K与深度z之间的关系,绘制出浸水前后参数K的计算结果随深度变化趋势图(见图8)。从图8可以发现:浸水前后的K-z曲线呈向上凸起的形状,并最终有保持不变的趋势,这说明K值会随着深度的增加按照增幅逐渐减小的趋势递增,并最终保持不变,此外,浸水后的K值较浸水前的更小。
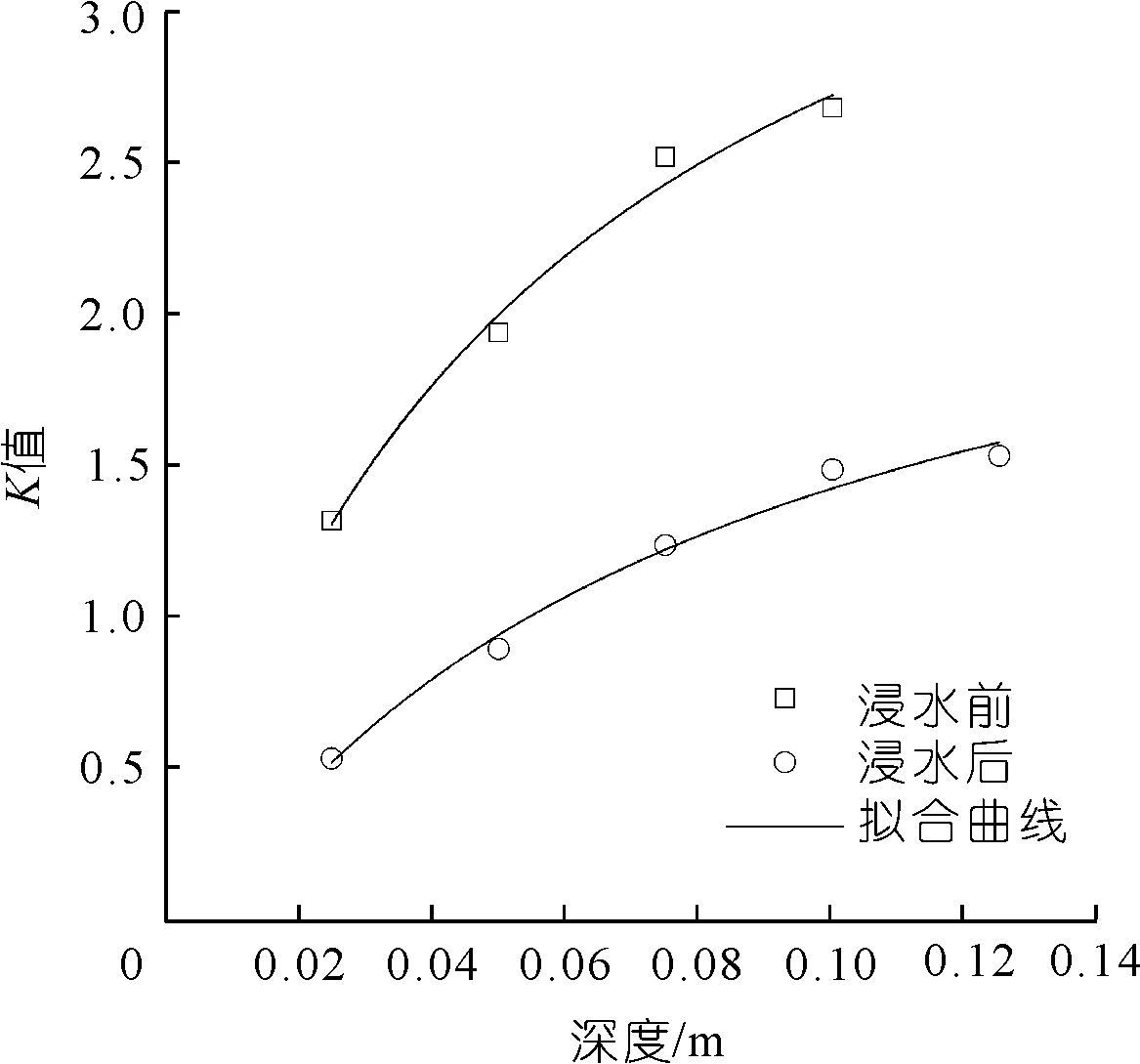
图8 参数K随深度z变化曲线Fig.8 Curves of parameter K varying with depth z
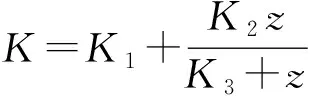
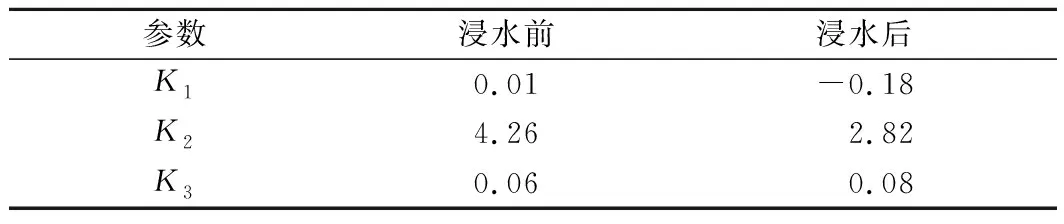
表5 参数K1,K2,K3的计算结果
确定浸水前后参数K与深度z之间的关系后,代入Pu=KACuD即可得出浸水前后Pu的具体表达式。
3.2.3B的确定
由于实测的p-y曲线中的土抗力都未达到极限土抗力值,因此无法确定Y100的值,即参数B无法确定。考虑膨胀土和黏土性质相似,因此可参考黏土中参数B的取值情况。参数B基本不随深度变化,一般与土质情况相关,其取值范围可随着土体的软硬程度取9~12之间,软质土取小值,硬质土取大值。
3.3 理论p-y曲线的建立
在上述中已将p-y曲线理论计算公式的基本形式和未知参数确定了,因此可得出膨胀土浸水过程中的p-y曲线理论计算公式为
(6)
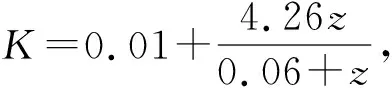
4 理论p-y曲线验证
以本文试验结果为例,利用建立的理论p-y曲线公式和已知的桩身水平位移,计算出不同深度桩周土抗力值。理论p-y曲线与实测p-y曲线对比如图9所示。从图中可以看出,浸水前后理论p-y曲线与实测p-y曲线整体上较为吻合,但浸水后1D深度的理论p-y曲线与实测值存在一定的误差。这是由于采用理论方法进行计算时,参数B的取值为9,参考了软黏土的取值范围,与软黏土不同的是,膨胀土浸水后地层隆起高度会随深度逐渐降低,对上层地基的影响较大,所以1D深度的计算值与理论值还存在一定的误差,说明本文方法也存在一定的局限性,这也是下一步研究的重点。
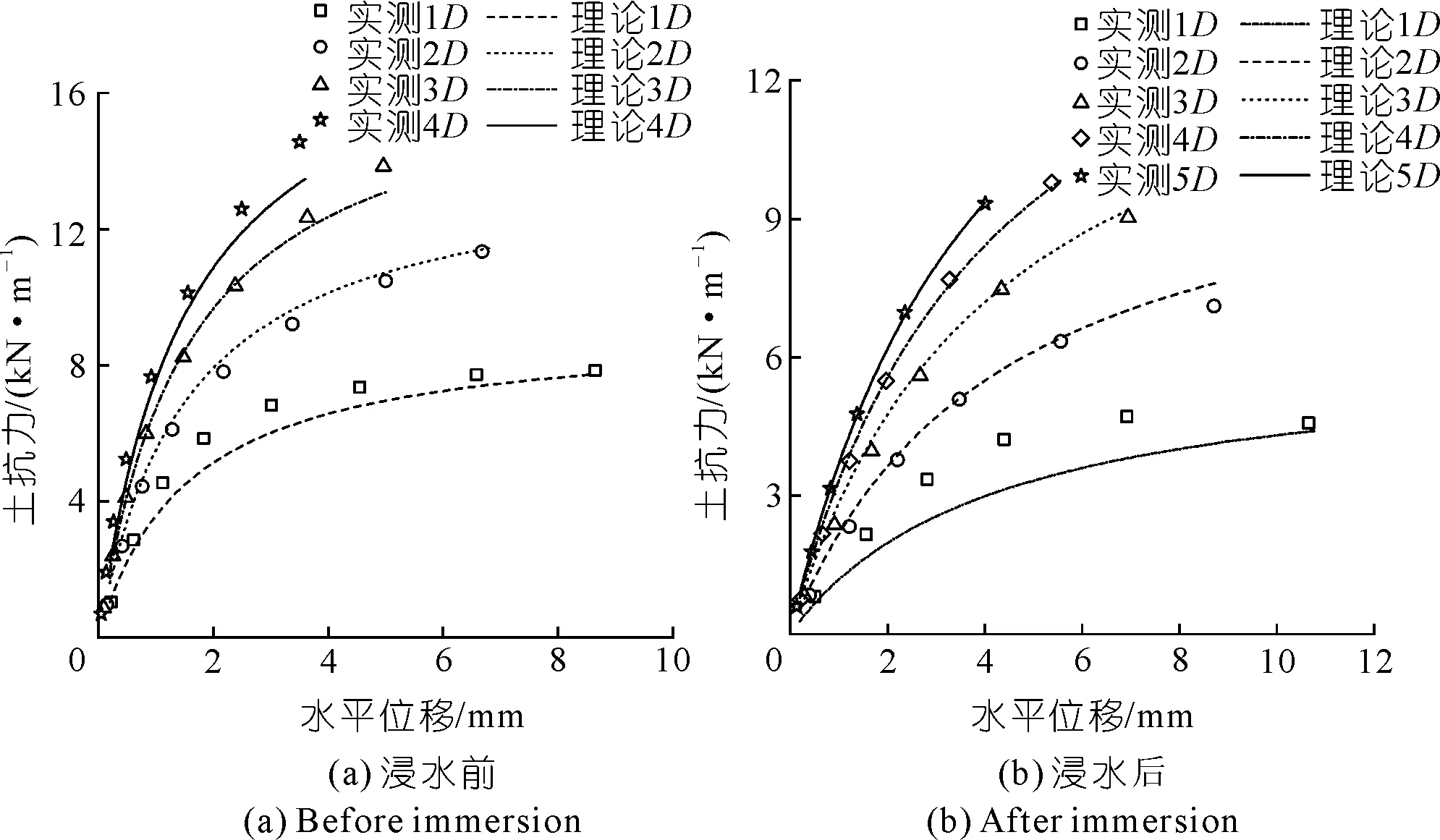
图9 理论p-y曲线和实测p-y曲线对比Fig.9 Comparison of theoretical p-y curves and measured p-y curves
5 结 论
本文通过室内模型试验和理论结合的方法,对浸水前后的膨胀土地基中水平受荷桩的位移、桩身弯矩及p-y曲线进行研究,得出了如下结论:
(1) 浸水前后的土抗力随着水平位移的增加而逐渐增大,最终基本稳定。浸水后的桩侧土抗力最大值降低,水平位移较浸水前增大明显。
(2) 浸水前后桩身水平位移的中性点分别位于桩身0.21 m(8D)和0.25 m(10D)位置。浸水后的中性点略低于浸水前,且土抗力最大值略有降低。
(3) 浸水前后桩身分布规律相似,均为先增大后减小。浸水前后桩身弯矩最大值位置分别为埋深0.10 m(4D)和0.12 m(4.8D)附近。浸水后的桩身弯矩最大值位置降低,且桩身弯矩较浸水前的有所增大。
(4) 以试验数据为基础,建立了浸水前后膨胀土地基中的水平受荷桩p-y曲线计算公式,并对计算公式进行了验证,计算结果与试验数据较为吻合。
