穿越管道滑坡地表位移预警阈值及预警模型研究

2023-02-12葛华，方迎潮，朱建平，李虎，王庆，时建辰

人民长江 2023年1期

葛华，方迎潮，朱建平，李虎，王庆，时建辰

(1.国家管网集团西南管道有限责任公司，四川成都 610041； 2.四川省地质工程勘察院集团有限公司，四川成都 610072)

0 引言

管道作为油气的主要运输手段，承担着中国70%的原油和90%的天然气运输[1]，助力着中国的经济发展。由于中国地形地貌特点，长输油气管道不可避免地穿越滑坡区，其中尤以西南管道公司所辖管道为甚。资料显示，西南管道公司所辖管道中，山区管道占比超过70%，管道沿线地质环境条件复杂，其中穿越大量的滑坡区，滑坡灾害发育引发管道周围土体发生变形，从而会导致埋地管道产生弯曲、压缩、扭曲、拉裂、局部屈曲等破坏行为[2]。

国内外计算滑坡区管道位移力学模型常将滑坡作为力荷载形式并作为主动力，在此基础上，梁政[3]运用弹性地基梁理论对管道横穿滑坡时的受力行为进行了推导；邓道明等[4]首次得出拉、压当量轴力下管道的内力及变形的计算公式；郝建斌等[5]假设管后土体为刚性楔形体，并对横穿滑坡时管道所受的推力进行了推导。许多学者根据滑坡位移塑性变形[6]、Pasternak双参数模型[7]、土体位移四次分布假设[8]等对滑坡管道的位移进行了理论推导。但是，以上滑坡管道位移力学模型的研究多以力荷载作为主动力，不便于体现管道极限位移与土体位移之间的关系，对滑坡监测工程有着一定的局限性。

最早对滑坡灾害预警预报的方法是在20世纪60～70年代，包括通过观察地表变形时间、地下水变化异常、地表裂缝的变化和动物的异常表现等状况判断滑坡是否即将失稳的现象预报法，以及斋藤法、位移时间曲线变化判断法、统计数学模型法和参数预报法等位移预报模型[9-11]。不少学者针对管道与滑坡的相互关系提出了不同的监测预警模型，日本学者Yasuhiro[12]利用分布式滑坡概念模型估计强降雨条件对浅层滑坡的影响；刘人杰[13]以川气东送普光-宜昌段为例，开展了滑坡与管道变形的监测预警研究；俞政[14]运用灰色模型对忠武输气管道滑坡段进行了预警研究；李岩岩[15]以西南某天然气管道为例建立了滑坡管道预警模型；冷建成等[16]根据管道应力监测数据，采用BP神经网络作为管道应力变化预警模型；陈星明[17]通过监测管道的变形确定预警等级；许强等[18]提出了一种改进的切线角及对应的滑坡预警判据，解决了位移与时间量纲不统一的问题。但以上研究均未对管道滑坡灾害的地表位移和地下水预警阈值指出定量化阈值计算方法，也未形成多因素下的预警模型。

本文将根据弹性地基梁模型，以弹性地基梁模型推导管道位移力学模型，结合管道最大位移和地表位移的耦合关系，以及地下水与滑坡稳定性的关系，确定地表位移和地下水预警阈值计算方法，并与管道应力监测预警相结合建立管道滑坡灾害多因素耦合预警模型。

1 横穿滑坡管道极限位移计算

众多学者针对管道极限位移计算多采用均布力荷载[19]、二次型力荷载[20]或楔形体力荷载[5]形式计算管道的变形特征，在实际监测工程中，以力的形式计算得到的管道变形特征并不能完全表示管道屈服时能达到的极限位移值，不便于监测预警。以弹性地基梁模型为基础推导管道力学方程，省略了滑坡推力的计算，运用管道位移与应力之间的相互关系进行推导，能为监测预警提供管道极限位移值，为预警阈值提供基础。因此，本次研究运用半无限连续弹性地基梁模型推导管道在横穿滑坡作用时能承受的极限位移。

1.1 非滑坡区管道力学行为

由于非滑坡区管道为小变形，且管道受到力始终处于平衡状态，可将此段看作是半无限连续弹性地基梁B模型，如图1所示，则此段的控制微分方程如式(1)所列。

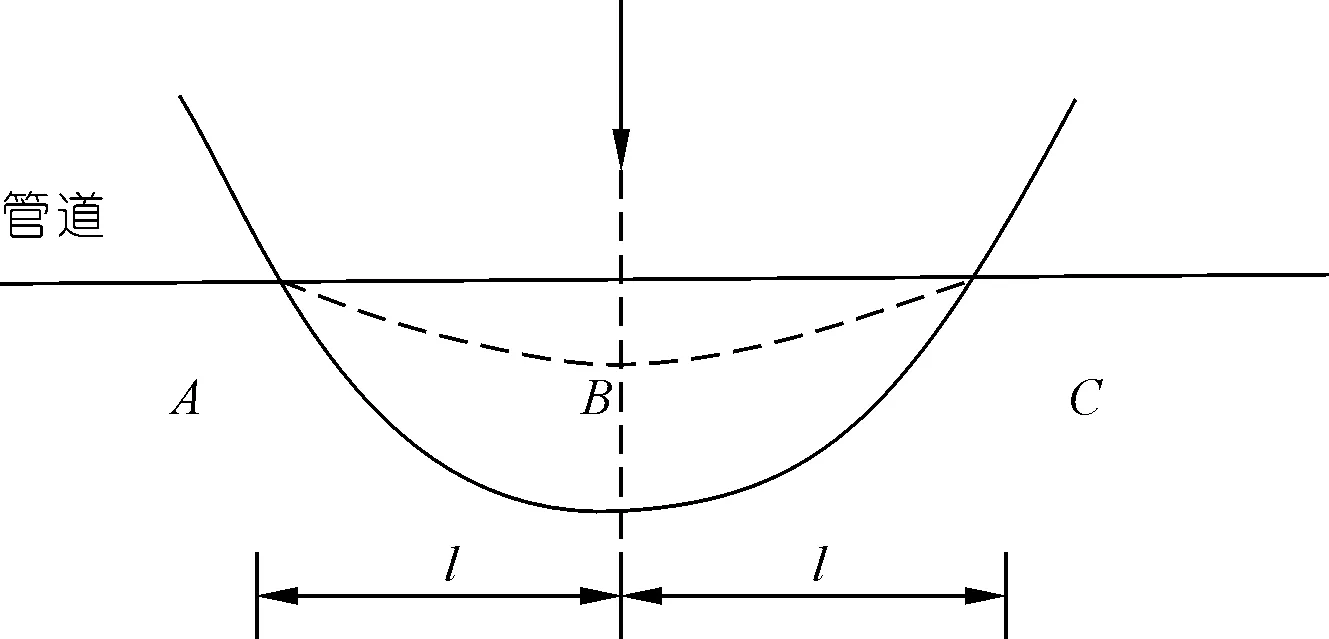
图1 管道穿越滑坡示意Fig.1 Schematic diagram of pipeline crossing landslide

(1)

式中：EI为管道的弯曲刚度；x为管道一点距A点的距离，m；y为管道挠度，m；k为弹性地基系数。

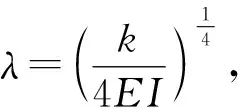
设A点的弯矩为MA，则可得到方程的解为

(2)

则根据挠度、转角、弯矩之间的相互关系可以求得在A点处的挠度(y)、转角(θ)、弯矩(M)和剪力(Q)如下：

(3)

1.2 横穿滑坡区管道位移

当管道横穿滑坡时，可将管道变形看作是对称变形，邓道明等[4]将管道简化为梁，假定滑坡区管道只受均匀滑坡推力，因此，本次研究在前人的理论基础上，运用弹性地基梁模型推导管道力学模型，将管道受到的滑坡作用简化为受上部土体的均布荷载，可将管道看作是受均布荷载的弹性梁模型。因挠度的四阶导数等于横向荷载，则将AB段设为

y=a4x4+a3x3+a2x2+a1x+a0

(4)

由于管道的连续性，则在A点处的力学行为与非滑坡区管道力学状态相同，又因为滑坡主滑面B点处其转角为0，且滑坡不断蠕变过程中管道上B点的位移逐渐变大，B点的最大位移即为管道跨中极限位移值，则边界条件为

(5)

式中：S为跨中B点位移，m；l为A点到B点的水平距离，m。

联立式(3)～(5) 可解得AB段挠度方程和在A点的弯矩为

(6)

(7)

由上一节可知，AB段与BC段对称，则整段的挠度方程可由分段函数表示为

(8)

(9)

由于管道在正常运行内压下工作，忽略温差的影响，因此管道总轴向应力σ为弯曲产生的轴向应力σ1与内压产生的轴向应力σ0之和。

(10)

式中：μ为管道泊松比；P为内压，Pa；D为管道外径，m；t为管道壁厚，m。

因此，通过式(10) 可确定管道弯曲产生的最大应力，结合式(7)和(9) 通过迭代算法，即可求出当总轴向应力达到屈服时的最大位移量S，并可通过不同x值计算得到滑坡位移分布。

2 滑坡地表位移预警阈值

根据以上滑坡动态变化过程，可知滑坡地表位移是造成管道破坏的最主要因素，针对缓慢型变形滑坡，将管道应力与滑坡形变相结合，运用式(7)，(9)，(10) 可计算得出管道能承受的最大位移值，并进行简化，以最不利方式考虑，即管道与滑坡看作是协同变形，管道的变形位移值就等于土体变形位移值。

将管道挠度达到90%的最大挠度作为滑坡形变指标红色级预警阈值，即S红=0.9S，此红色级预警表示管道在此时刻已经受力非常大，极有可能在极短的时间内发生屈服，达到管道破坏。因此，此红色级预警时间点应是管道最危险的时刻，维护工作需在此阶段之前结束，若未结束则维修人员需立刻退场，对管道进行关阀等相关措施，保障人员与管道安全。

为了安全考虑，以管-土协同变形为最不利状态，则滑坡形变位移预警的蓝色级预警以滑坡开始运动为指标，以GNSS地表位移监测设备为例，设备的精度为±5 mm，且考虑到监测受干扰等异常情况，监测数据误差符合3σ原则(σ为设备精度)，则取滑坡地表位移监测数据达到15 mm作为蓝色预警阈值。蓝色预警时应时刻关注灾害体变形情况，做好应急处理准备措施，以及在此刻考虑灾害的危险性等。

利用地表位移监测数据可以得出一段时间内的地表变形速度V，以1月以内的平均形变速度确定，若监测工程较为紧急，则可适当降低变形速度获取周期。以管道挠度达到红色级预警时的挠度(0.9S)与地表变形速度V相除，得到滑坡以此速度进行发育时管道能达到破坏的时间T红=0.9S/V，按照抢修时间和人员调动总时间t，反算出黄色预警时间点T黄，如下式：

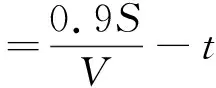
(11)

根据式(11)计算得出的黄色预警时间，结合地表位移S、时间T和变化速度V的关系，即可得到黄色预警时间下地表位移预警阈值，如式(12)所示。黄色预警时则应是灾害点处理开始时间点，需要预留时间对灾害点进行处理和维护，防止灾害发生，减小灾害发生所产生的损失。

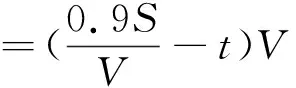
(12)

因此，以监测数据达到15 mm作为地表位移蓝色预警阈值S蓝，以式(12)计算得到的S黄作为地表位移黄色预警阈值，以管道挠度达到90%的最大挠度S红作为滑坡形变指标红色级预警阈值，如表1所列。

表1 滑坡地表位移预警级别划分标准

3 滑坡地下水位预警阈值

由滑坡动态变化过程可知，地下水与滑坡稳定性有着密切的联系。在降雨条件下，外界环境发生改变，雨水入渗到斜坡体内部，改变了其原有的地下水深度及岩土体物理力学状态，滑坡体地下水位变高，降低了滑面的强度指标，从而也使抗滑力减小，当稳定系数K突破临界值1时，斜坡体极有可能产生破坏，出现变形，进而可能演变为滑坡灾害。有许多研究[21]都对地下水对滑坡稳定性的关系进行了分析。

研究的主要问题是需要解决抗滑力与地下水深度之间的关系。在地震作用下，降雨型滑坡稳定性计算模型如图2所示。

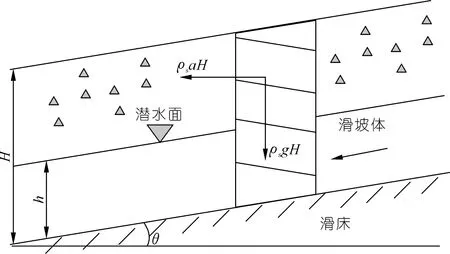
图2 降雨型斜坡地下水计算模型Fig.2 The calculation model of groundwater for rainfall type slope

考虑地震作用和降雨条件，将潜在滑坡体简化为二维平面问题。由于雨水下渗作用，潜水面上升，潜水面高度变大使得滑坡稳定性降低，进而可能导致滑坡产生。假设斜坡堆积体的厚度为H，地下水位高度为h，斜坡的滑面倾角为θ，近似取坡度值。根据莫尔-库伦定律以及极限平衡理论计算斜坡体的稳定系数K，计算公式[21]如下：

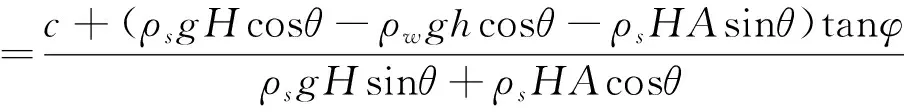
(13)

式中：R为单位斜坡体的抗滑力，kN/m；T为单位斜坡下滑力，kN/m；c为斜坡体的有效黏聚力，kPa；ρs，ρw分别为坡体物质和水的密度大小，kg/m3；g为重力加速度值，m/s2；A为地震加速度，m/s2；H表示斜坡体的铅直厚度值，m；h表示水位；φ为坡体有效内摩擦角；θ为斜坡的倾角。

根据稳定性系数K的计算公式可知，斜坡的稳定性K与水位h呈负相关关系，当h不断增大时，K逐渐减小。运用式(13)反算滑坡体临界水位，得到稳定性系数与滑坡水位关系式(14)：

(14)

依据GB/T 32864-2016《滑坡防治工程勘查规范》[22]知稳定性系数K<1为不稳定状态；1≤K<1.05 为欠稳定状态；1.05≤K<1.15为基本稳定状态；K≥1.15为稳定状态。

根据不同稳定性系数代入式(8)计算得出滑坡地下水位，以K=1.15，1.05和1计算得到的地下水位高度H1，H2和H3分别作为蓝色、黄色和红色级预警阈值，得到以地下水位为监测预警的各级预警阈值，如表2所列。

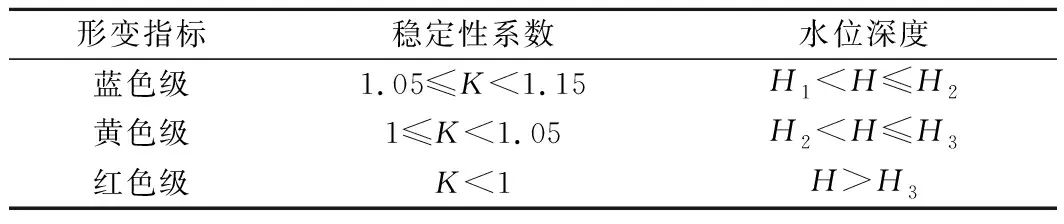
表2 地下水位预警级别划分标准

4 多因素耦合预警模型

4.1 滑坡耦合预警模型

将滑坡地表位移和地下水高度相结合构建滑坡本体二维预警模型，以滑坡地表位移预警为主，以地下水位预警为辅，得到滑坡耦合预警模型，如表3所列。

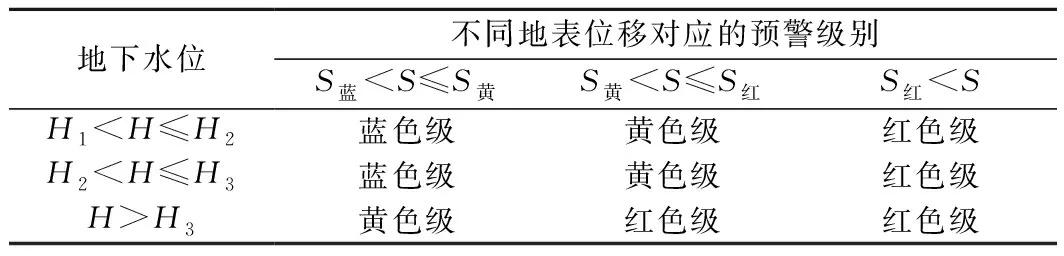
表3 滑坡地表位移与地下水位的二维预警模型

4.2 滑坡与管道耦合预警模型

管道穿越滑坡区时，其主要关注对象为管道是否达到破坏，需要对管道本体应力进行预警，以便了解管道应力的动态变化。参照相关规范[23]，将管道应力σ预警分级规定为管道附加应力[σ]T的30%，60%，90%作为蓝色预警、黄色预警和红色预警阈值，即管道应力预警级别划分如表4所列。

表4 管道应力预警级别划分

将滑坡本体预警与管道应力预警相互耦合，以直接反映管道动态变化的应力预警为主，以诱发管道破坏的滑坡本体预警为辅，建立管道滑坡灾害动态耦合预警模型，如表5所列。若现场监测方式仅有一种或两种，则根据相应的设备进行预警阈值设置。

表5 管道滑坡灾害二维预警模型

此模型可广泛应用于管道穿越滑坡灾害的预警当中，当实际工程中存在地下水、地表位移和管道应力监测时，则完全适用于此模型；当未有地下水或地表位移其中一种监测时，以另一种作为滑坡预警等级，结合管道应力实现二维预警。当实际工程中未有管道应力监测，则根据地表位移和地下水实现一维预警或二维预警。

5 案例分析

将以上预警阈值计算与预警模型运用到贵州K0937+050滑坡上，该点位于贵州省盘州市，总体形态呈不完整“舌状”，海拔高度约1 560～1 600 m，高差约40 m，斜坡坡度整体约18°。滑坡后缘以斜坡后部裂缝上方为界，前缘以房屋后部为界，左右两侧以地形陡缓变化处为界。该滑坡纵长约100 m，横向宽平均70 m，滑坡体厚约3 m，整体方量约1.5万m3，为小型牵引式土质滑坡。滑体物质组成为粉质黏土，滑面初步推断为基覆界面，场地地震动峰值加速度值为0.05g，对应的地震基本烈度为Ⅵ度，地震动反应谱特征周期为0.35 s，设计地震分组为第一组。

根据现场滑坡勘察，土体参数根据室内试验综合取值，在饱和状态下，土体重度为18.5 kN/m3，土壤黏聚力C为14 kPa，内摩擦角φ为11°，弹性地基系数取值为3.0×104kN/m3，g取9.8 m/s2。滑坡中部滑体土的渗透系数为1.74 m/d，渗透性较好，地下水埋深为0.9～1.2 m。

灾害点内有一干线管道，从滑坡中前部横向敷设，管道埋深2 m左右，受影响管道长约80 m。管线管材为X80，直径为1 016 mm，壁厚为15.3 mm。设计内压为10 MPa。现阶段该点共布设4处GNSS地表形变监测站，2号和4号地表形变监测站位于滑坡主滑剖面上，1号和3号地表形变监测站位于滑坡中部主滑剖面两侧，如图3所示。根据监测数据显示，从2021年6月15日至8月1日，监测区地表形变监测区累计最大形变量为29.978 mm，位于2号监测点，整体变化趋势平缓，处于蠕动变形阶段，如图4所示。

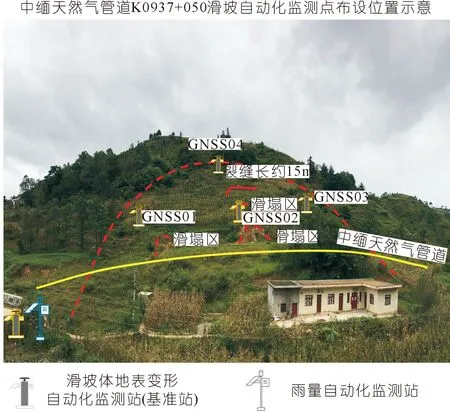
图3 滑坡体全貌Fig.3 General view of the slide

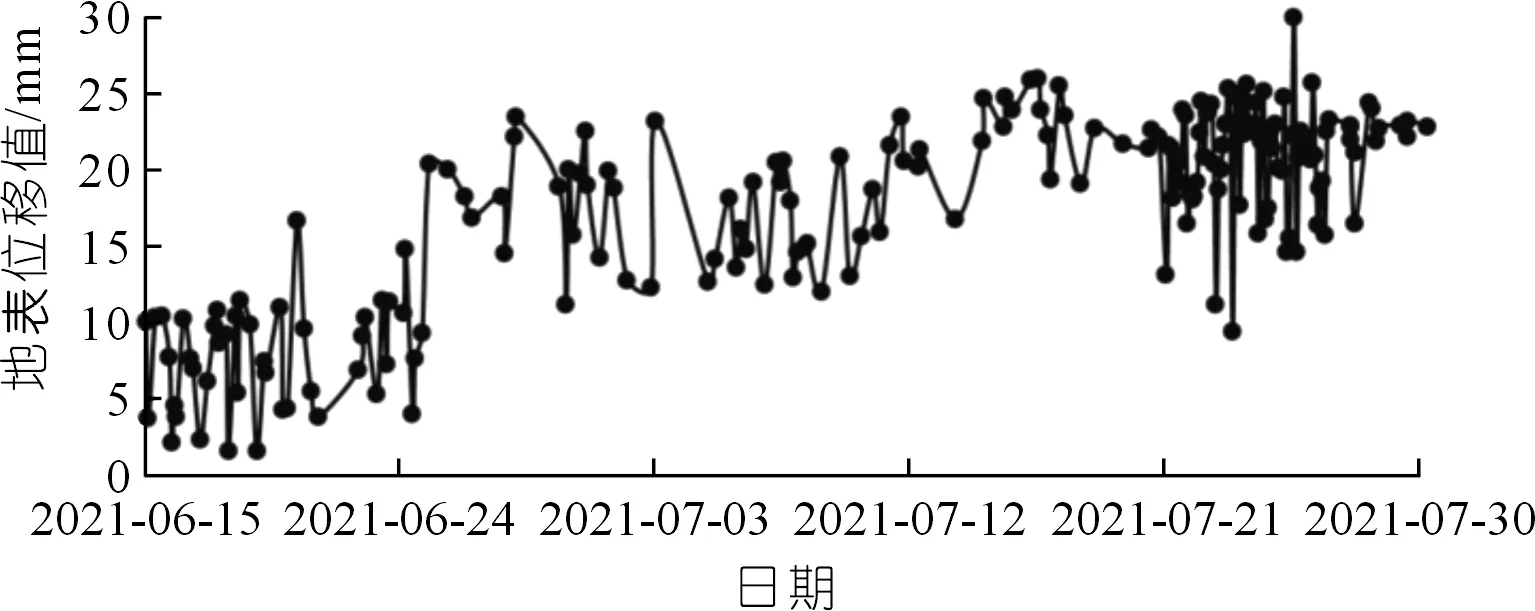
图4 2号监测点地表位移数据Fig.4 Surface displacement data of No.2 monitoring site

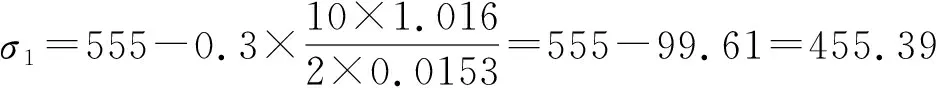
(15)

随后将MA，λ，l，D代入式(9) 中得到管道应力σ1关于位移S和位置距离x的关系如下：

(16)

由于2号监测点位于滑坡跨中，因此将x=35 m，应力σ1=455 390 000 Pa代入式(16)中，化简计算得到位移如下：

(17)

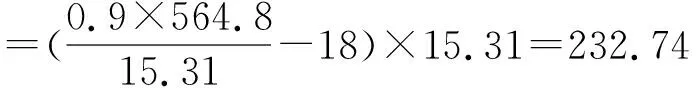
将勘察得到的土体重度ρs、黏聚力C、内摩擦角φ、滑坡体厚H、地震加速度A、斜坡坡度θ、重力加速度g带入式(14)中得到地下水位与稳定性之间的关系，简化得h=13.26-10.98K，则当稳定性系数为1时，地下水位为2.28 m，为红色预警阈值；当稳定性系数为1.05时，地下水位为1.73 m，为黄色预警阈值；当稳定性系数为1.15时，地下水位为0.63 m，为蓝色预警阈值。

经勘查，现阶段滑坡处于缓慢蠕动变形阶段，地下水位埋深为0.9～1.2 m之间，则地下水位高度为1.8～2.1 m，故地下水位预警达到黄色级。

根据相关规范[22]得到管道允许附加拉应力阈值为406 MPa，则蓝色预警阈值为0.3×406=121.8 MPa；黄色预警阈值为0.6×406=243.6 MPa；红色预警阈值为0.9×406=365.4 MPa。由于管道尚未发生明显移动，由管道形变特征显示未达到蓝色预警阈值，处于正常范围，故不产生预警。

综合地表位移和滑坡地下水预警结果，结合表3，该点现阶段应报关注级预警。经实勘，现场局部出现滑移沉降，在滑坡前缘较为明显。坡体出现局部下错如图5所示。案例表明，运用综合预警模型在一定程度上能预警埋地管道滑坡灾害的发生，能结合滑坡和管道变化特征综合分析管道穿越滑坡灾害危险性，减少预警错报、漏报，能在一定程度上提高管道滑坡预警准确率，为管道安全运营及时提供决策参考信息，减轻灾害影响，降低经济损失。