基于多演化阶段插值方法的滑坡预测研究

段 功 豪，马 迅，付 杰

(1.武汉工程大学 计算机科学与工程学院，湖北 武汉 430205； 2.武汉工程大学 智能机器人湖北省重点实验室，湖北 武汉 430205； 3.中国地质调查局 水文地质环境地质调查中心，河北 保定 071051)

0 引 言

滑坡是一种在山区或丘陵地区十分常见的地质灾害。据自然资源部统计，2021年上半年中国共发生地质灾害1 150起，造成17人死亡，3人失踪，直接经济损失达24 084.9万元，其中滑坡高达579起，因此对滑坡精准的预测可以极大程度地减少损失。

影响滑坡发生的因素有很多，其中位移是滑坡预测的主要因素之一。从20世纪80年代开始，国内外普遍使用数学模型来拟合监测点的位移-时间曲线进行分析，从而预测滑坡位移的动态趋势变化。其中影响预测结果准确性的除了模型方法，还有对滑坡监测数据的预处理方法[1-3]。阶跃型滑坡具有明显的演化区间，在实时收集监测点数据时，可能发生仪器故障或受外界影响，产生部分异常的数据，因此数据插值方法的好坏直接影响数据收集的准确性[4]。相关预处理所用的插值算法有很多，Lagrange插值法、均差的牛顿插值法、线性插值法、埃尔米特插值法和三次样条插值法等[5]。传统的直接插值方式是将整体的数据带入插值算法从而算出相应插值，不仅无法保证整体曲线的光滑性，而且会产生龙格现象，极大降低了插值的精确度。所以有时需要将整条曲线进行全局分段插值，缩小数据量可部分提高准确性，但由于通过同一指标分段，降低了分段数据与不同演变阶段之间的关联，尤其对于阶跃型滑坡，在拐点附近会出现较大的误差。

因此，在对曲线分段时使用什么算法、对哪些点进行插值、应在曲线上选取哪些点作为分段点，成为学者们广泛讨论的问题[6-7]。基于上述研究背景，本文选择目的性强、灵活度高的Lagrange插值法；为保证最后预测的准确性，插值点的选取不仅需解决数据的缺值异常值，有时还要确保数据的等距性，根据需求设置插值点；在插值分段选取上，根据不同的演化阶段，以拐点作为分段点，将曲线分为相应的区间，对每个区间进行局部分段插值，既保证了插值的整体关联性，又能稳定插值与当前运动情况的准确性；最后对白家包滑坡的累积位移-时间曲线进行基于实际运动学变化情况的插值，并对比验证了该方法的准确性。

1 研究区概况

白家包滑坡属于典型的阶跃型滑坡，位于宜昌市秭归县归州镇向家店村，处于香溪右岸[8]。通过图1无人机拍摄可见，周围地貌部位为低山区凹形斜坡，前缘直抵香溪河，滑坡剪出口位于高程125～135 m处，滑坡后缘以基岩为界，高程265 m，滑坡左侧以山脊下部基岩为界，右侧以山梁为界，前缘宽500 m，后缘宽300 m，均宽400 m，纵长约550 m，滑坡面积22万m2。滑坡平面形态呈短舌状[9-11]。深层滑体前缘厚20～30 m，中部厚47 m，后缘厚10～40 m，滑体平均厚度45 m，滑体体积990万m3。浅层滑体前缘厚10～20 m，中部厚35 m，后缘厚10～40 m，滑体平均厚度30 m，滑体体积660万m3[12]。此地气候类型为亚热带季风气候，且有明显的峡谷气候特征，降水丰沛，四季分明，年平均降雨量为1 000～1 400 mm，降雨多集中于夏季，是暴雨高发地区之一。三峡峡谷深邃，风力较强，风向固定，为东西向的顺峡方向。勘探资料显示，此地滑坡体的土壤物质成分由粉质黏土混合碎块石土组成，土质松散且杂乱。如图2滑坡体剖面图所示，滑床物质主要由侏罗系下巴东组的长石石英砂岩及泥岩组成，岩层倾向为260°～285°，倾角为30°～40°[13]。滑坡前缘大部分浸没在河水中，当水库水位上升至175.00 m时，部分滑体将完全淹没于水中。山体植被覆盖率较好，主要由亚热带阔叶林和部分山地灌草丛组成，但在山体上部有部分裸露的土壤岩石，在下部有数十户居民，以及几百亩开垦过的农田，其中还有一条秭兴公路从中穿过，因此若此地发生滑坡，将造成巨大的损失。

图1 白家包滑坡全貌Fig.1 Full picture of the Baijiabao landslide

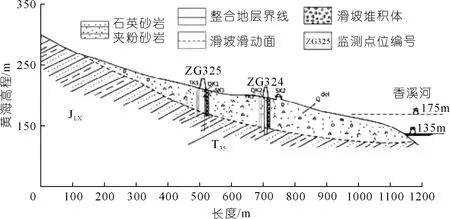
图2 白家包滑坡体剖面图Fig.2 Section of Baijiabao landslide mass

为了保障村民的生命财产安全，白家包滑坡在2006年10月开始采用GPS对地表位移进行监测，建设有ZG323、ZG324、ZG325和ZG326共4个监测点，其中ZG324和ZG325位于滑坡主滑坡面，ZG323和ZG326位于滑坡中下部靠近秭兴公路附近[14]。这4个监测点的位移方向与坡向一致，各个监测点每月不定期监测1次，夏季6～9月每月监测2次[15]。各仪器均有较高的精度，可精确到小数点后10位。

2 研究方法

2.1 插值算法

本次研究采用的拉格朗日(Lagrange)插值算法结构整齐、实现方便，具体多项式如下：

(1)

其中每个lj(x)为Lagrange基本多项式(或称插值基函数)，其表达式为

(2)

对于分析监测点的位移-时间的数据，每个时间和对应的监测值可以作为一个坐标点，x为横轴的时间，y为纵轴的监测值，所有的监测数据都可以通过(x，y)表示。将n个监测点(x0，y0)，(x1，y1)，…，(xn，yn)带入n项拉格朗日多项式中，通过输入插入时间x，可算得此刻的插值大小。

在计算插值误差时，通常计算多项式余项来作为插值的误差，由公式(1) 可知，y=f(x)的Lagrange插值是Ln(x)，其误差公式为

(3)

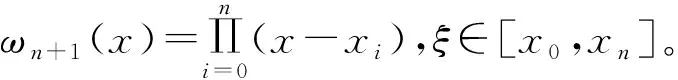
通过公式可以发现，Lagrange插值法根据阶数的不同，可以演化出不同的插值算法：当多项式是一阶函数时，是线性插值算法；当多项式取二阶时，是抛物插值算法；取三阶时，相当于三次样条插值。因此，根据实验的需要，灵活地设置阶数，便于进行理论分析[16]。随着节点数的增多，阶数的上升带来了高次计算量的增大，插值点的误差被无限放大，从而导致了龙格现象，当曲线斜率越大时，龙格现象越明显。为避免龙格现象的发生，在分析数据较多的滑坡位移数据时，往往使用分段插值法，如分段线性插值法、三次样条插值法等Lagrange低阶插值法，但插值的整体关联性减弱了，因此应根据不同的插值应用背景，科学设置相应的目标函数与动态实现过程。

2.2 指数平滑算法

指数平滑预测法是指通过一个平滑系数，将本期实际值与本期的预测值按比例相加，最终得到下一期数据的预测值的一种加权平均法，其依据时间序列的稳定性和有规律性的态势，进行合理的延续来达到对近期数据的预测。根据平滑次数不同，分为多种类型，在对滑坡易发性研究时，对斜率明显的曲线更适用于二次指数平滑法。二次指数平滑法必须与一次指数平滑法配合，即在一次指数平滑法的基础上再做一遍指数平滑，从而建立预测的数学模型，最后确定预测值。二次指数平滑的计算公式如下：

(4)

(5)

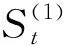
xt+T=AT+BTT

(6)

其中，

(7)

(8)

式中：T为未来预测的期数；AT与BT都是预测模型中的参数[17]。本次滑坡预测使用二次指数平滑模型时，由于数据量较大，靠前数据对模型影响较小，可将实际值代替预测值。

3 数据分析及预测分析

3.1 数据选取

在2006～2012年之间，根据白家包滑坡设置的4个位移监测点ZG323、ZG324、ZG325和ZG326获取到一共90期数据作为插值方法研究的对象。将获取的累积位移和对应的时间作为横纵坐标绘制累积位移-时间曲线图，如图3所示。

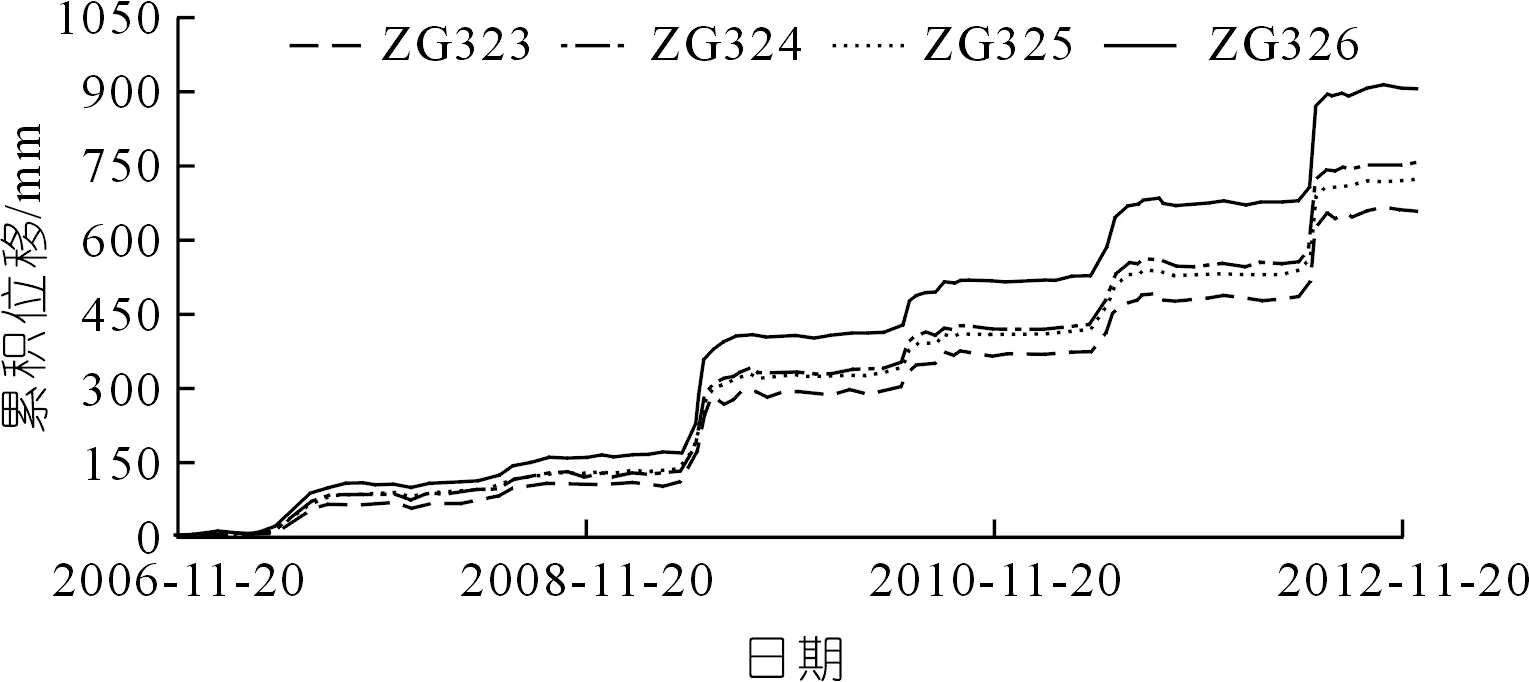
图3 白家包滑坡累积位移-时间统计Fig.3 Cumulative displacement-time curve of Baijiabao landslide

观察图3曲线，可发现明显的3大特点：① 具有同步性，4个监测点的累积位移的变化幅度均随时间同步改变，因此可只选取其中1条曲线作为研究对象；② 具有周期性，累积位移在每年的5～9月份会加速增长，其他时间相对较为平稳；③ 具有明显的增长趋势，从整体上看，曲线呈现出阶梯状的增长趋势，有明显的拐点，并且随着时间推移，累积位移的变化越来越明显，符合模型的应用特点。

根据其同步性，选取累积位移变化最明显的ZG326曲线作为白家包滑坡的研究对象，同时为方便插值计算，将日期通过做差转化为天数。在ZG326曲线中，将85期数据作为原始数据，后5期数据作为指数平滑的训练数据。由于使用了指数平滑法，为了保证每期数据的等距性，需要通过插值算法将数据变为以30 d为间隔的位移数据。

3.2 演化阶段划分

在1963年，日本学者斋藤迪孝提出了斋藤蠕变曲线模型[18]。如图4所示，通过观察斋藤蠕变曲线模型，滑坡形变有3个演变阶段，分别为初始形变阶段、等速形变阶段与加速形变阶段。研究成果表明：斜坡的稳定性状况与其变形阶段有着直接的联系，准确地把握斜坡的变形演化阶段是进行斜坡稳定性评价和滑坡预测预报的基础。从图4斜坡变形三阶段演化模式可以分析得出：在斜坡的初始形变阶段，当形变在外界因素的作用下突然启动后，随着外界因素减弱甚至消失，其变形速率会逐渐降低，其加速度为负值[19]；在斜坡的等速形变阶段，由于其速率基本维持在一恒定值，加速度基本为0；而一旦进入加速形变阶段，随着变形速率的不断增加，其加速度变为正值，并呈逐渐增大的趋势，超过一界限即表示滑坡进入一临滑阶段[20]。在本实验中，忽略初始形变阶段，将曲线按照等速形变阶段与加速形变阶段划分曲线区间，加速度平稳的等速形变划为平稳区间，加速度突变的加速形变划为加速区间，在平稳区间使用高阶Lagrange插值法，由于曲线斜率较小，不易发生龙格现象；在加速区间，由于斜率较大，使用低阶Lagrange插值法可以保证准确度更高。由于在每年5～9月份降雨增大以及白家包滑坡周期性的规律，往往每年5月以及9月为滑坡形变曲线的拐点，将其作为插值区间的划分。

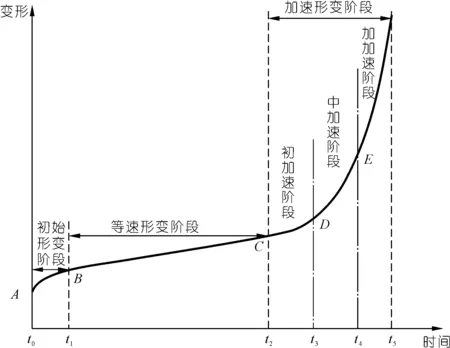
图4 斋藤蠕变曲线模型Fig.4 Saivine creep curve model

3.3 数据插值与预测分析

由于插值算法对曲线的加速度敏感，不同区间需要使用合适的插值算法。为了研究不同插值法对预测精度的影响，使用3种插值方法进行对比，分别为直接插值、全局分段插值和局部分段插值。直接插值是将全部85期数据代入Lagrange多项式，构成85阶Lagrange插值计算式的一种插值方法；全局分段插值是全程使用同一分段指标，使用一组全程7阶Lagrange分段插值的插值方法；最后一种方法是结合上述的滑坡演化区间，将平稳区间使用10阶Lagrange插值模拟高阶分段插值，加速区间使用5阶Lagrange插值模拟低阶分段插值，作为局部分段插值。经过直接插值、全局分段插值与局部分段插值后，结果如表1所列。

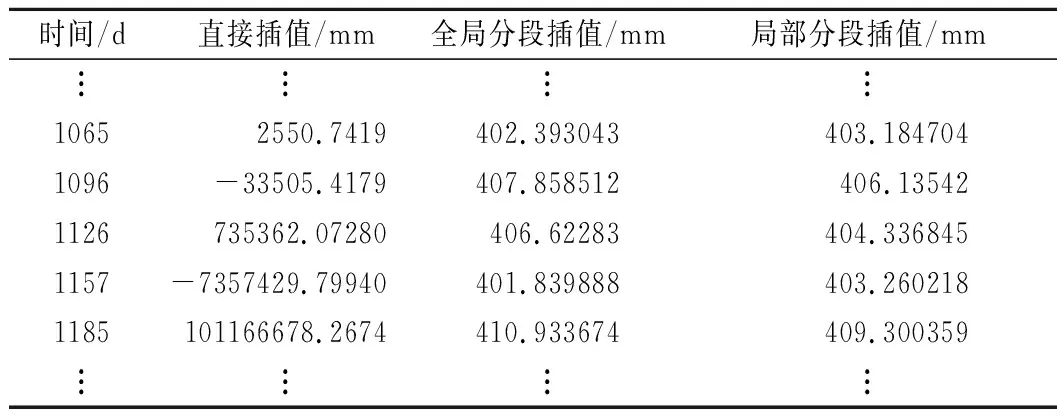
表1 插值数据对比

由表1可知，由于整体插值的数据过多，发生了龙格现象，造成了极大的误差，故舍去此方法。将经过插值的数据代入指数平滑算法中，设平滑指数为0.5，使用剩下5期数据训练，预测出近期的位移变化。为作对比，将原数据、全局插值后的数据与局部插值后的数据分别代入，具体结果如图5所示。

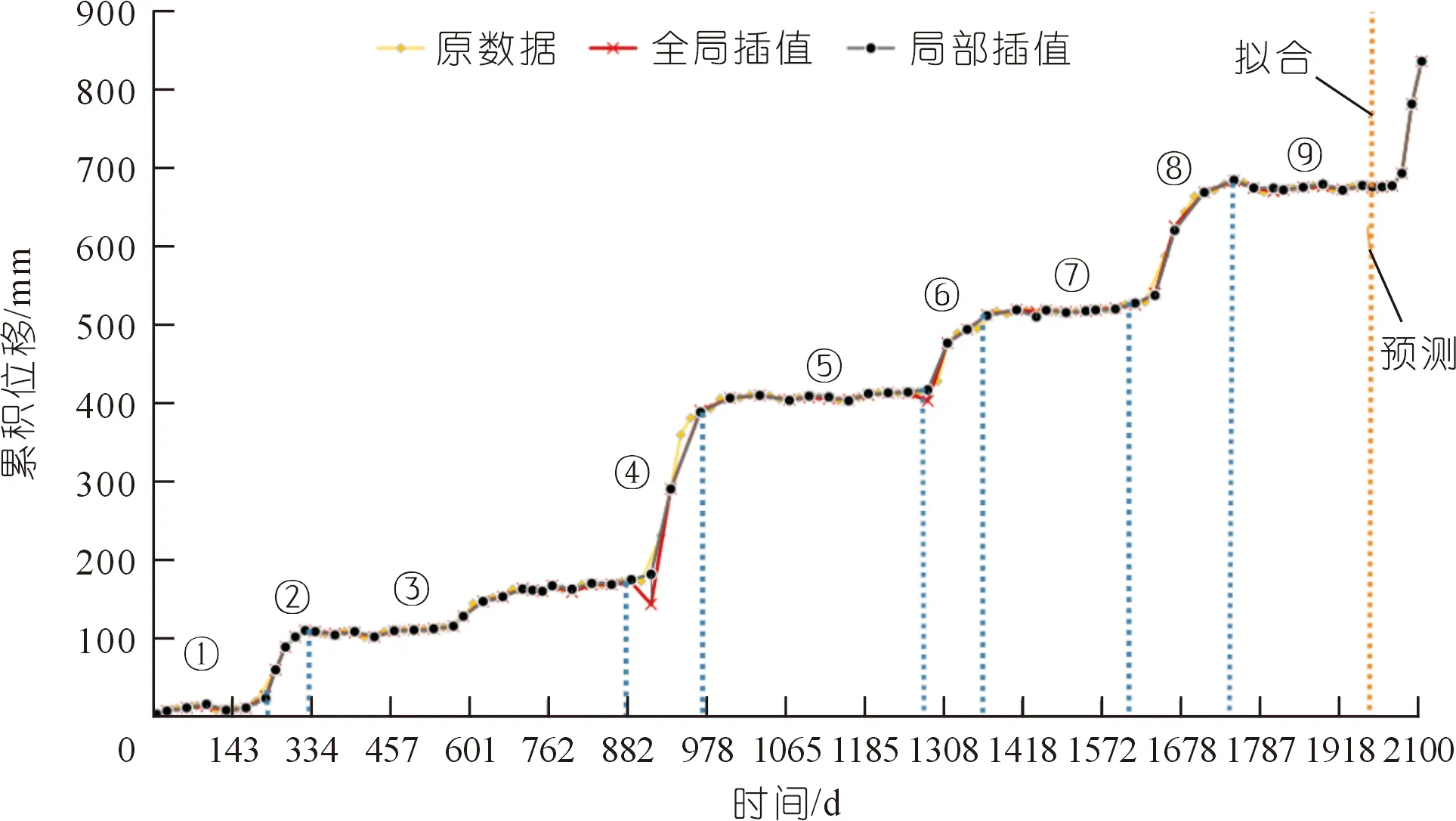
图5 滑坡累积位移插值预测对比Fig.5 Comparison of interpolation prediction of landslide cumulative displacement

图5中左边为位移插值对比，其中①、③、⑤、⑦、⑨区间为平稳区间，剩余较陡峭的②、④、⑥、⑧区间为加速区间。通过观察，在整体演变趋势上，3条曲线基本吻合滑坡的周期性位移形变规律，表现为在平稳区间前后变化较小，加速区间位移变化明显。通过具体分析，在加速区间上，全局插值曲线的拟合情况与原始数据较为偏离，而局部插值曲线与原数据曲线更为相似。这两列数据的具体误差如表2所列。

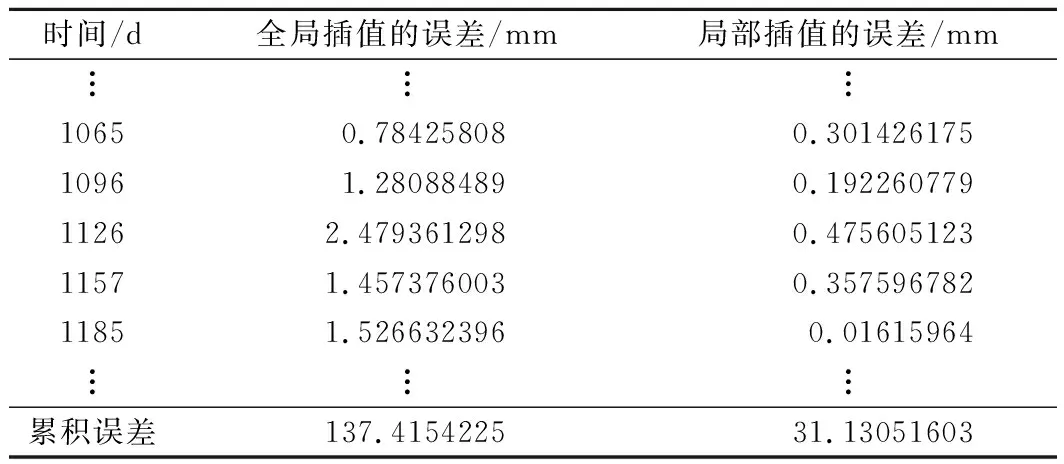
表2 插值误差对比

如表2所列，局部分段插值的误差相比于全局分段插值在各阶段的误差均小一些，在整体上，局部分段插值的累积误差相较于传统的全局分段插值降低了近100 mm。

在图5中，右边的6个数据为预测对比，可以发现曲线近期呈现加速上升的趋势。如表3所列，将3组数据放入指数平滑算法中，计算出第1 978天也就是2012年4月20日的预测值，然后进行5组数据的训练，最终可以预测出2012年9月19日的累积位移值，在误差方面，使用局部插值预测在训练上的误差较小，整体上，全局插值预测累积误差为1.33 mm，而局部插值预测累积误差为0.04 mm，提升了近1 mm。

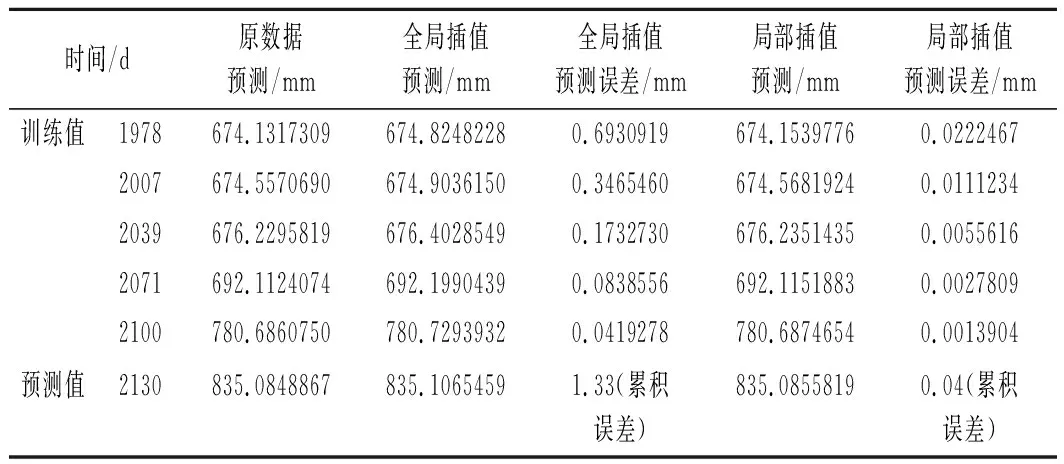
表3 平滑效果对比

4 结 语

本文针对阶跃型滑坡的准确位移预测提出了一种改进的Lagrange插值算法。该新算法在传统插值算法的基础上，根据Lagrange多项式的特点增加了先验分阶段的步骤，在不同阶段使用不同指标的插值方法。由于前后历史数据的敏感性不同，加速阶段和平稳区间采用不同阶数的数据拟合插值，能进一步反映滑坡在演化过程中的动态实时特点。最后通过实验证明了分段插值的方法误差更低，形成的位移预测值更精确，相较于传统方法更具有优势。本文在插值方法上提出了一个新思路，适用于有明显演化阶段的阶跃型滑坡类型，但对于形变曲线规律不明显的滑坡，找到关键拐点的方法还有待改进，为此需进一步研究。