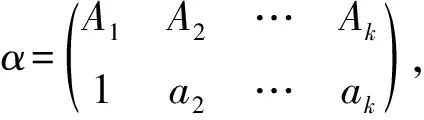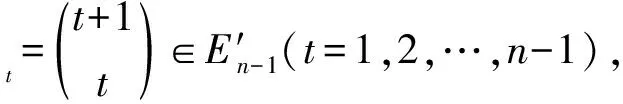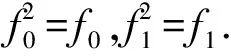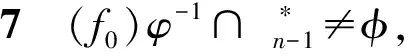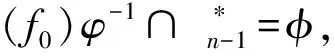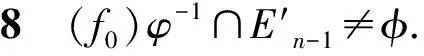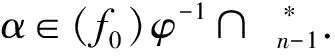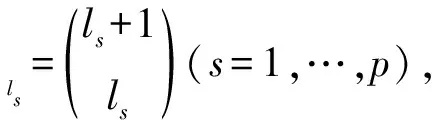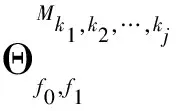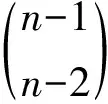保序递减变换半群的秩2自同态
2023-02-11杨秀良
阳 晶,杨秀良
(杭州师范大学数学学院,浙江 杭州 311121)
0 引言和主要结果

为了叙述清楚结果,需要下面符号和术语.
令E′n-1是Cn中所有秩为n-1的幂等元组成的集合.E′n-1中的任何一个元为
设f0,f1∈Cn是不同的幂等元且f0f1=f1f0=f0.任取k1,k2,…,kJ∈E′n-1,其中j∈{1,2,…,n-1}且k1 于是本文的主要结果是: 定理2设G={φ∈End(Cn)||(Cn)φ|=2},则 组成的集合: (1)t≤k; (2) 对任意的x∈Xn,有xβ≤xα; (3) 存在{as2,as3,…,ast}⊆im(α)使得 bi≤asi, minAsi≤minBi(i=2,…,t) 且1 证明任取β∈CnαCn,则存在γ,δ∈Cn使得β=γαδ,显然 t=rank(β)≤rank(α)=k, 且由于δ,γ是递减的,α是保序的,则对任意的x∈Xn有 xβ=xγαδ≤xγα≤xα. 对i=2,…,t,令z=minBi,因δ是递减的,则bi=zβ=zγαδ≤(zγ)α. 又令(zγ)α=asi,则可得bi≤asi且zγ∈Asi,从而minAsi≤zγ.又因zγ≤z=minBi,进而 minAsi≤minBi. 现在设i bi=xβ=(xγα)δ=(asi)δ, bj=yβ=(yγα)δ=(asj)δ. 由于bi 反之,设 满足上述(1)、(2)、(3)条件,令 且对任意的x∈Xn,令δ这样定义: 显然γ,δ∈Cn且β=γαδ.因此β∈CnαCn. □ Ωt={α∈Cn|(t+1)α 证明令Y={α∈Cn|(t+1)α (t+1)β≤(t+1)t=t 从而β∈Y,进而Ωt⊆Y. 反之,任取γ∈Y,则(t+1)γ (1) 显然rank(γ)≤n-1. (2) 对任意的x∈Xn,若x≠t+1,则xγ≤x=xt; 若x=t+1,因(t+1)γ (t+1)γ≤t=(t+1)t. (3) 令 显然 设 情形1im(γ)⊆im(t).令asi=bi(i=2,…,k),则显然(as2,…,ask)⊆im(t) 且1 minAsi=asi=bi≤minBi(i=2,…,k). 情形2im(γ)im(t),则t+1∈im(γ)且im(γ) 显然(as2,…,ask)⊆im(t)且1 minAsi=asi=bi≤minBi(i=2,…,k-1), ask=t+2>bk=t+1. 因(t+1)γ minAsk=ask=t+2≤minBk. 若j 子情形2.1bj+1>bj+1.对i=2,…,k,不妨令 显然(as2,…,ask)⊆im(t)且1 minAsi=asi=bi≤minBi(i≠j), asj=t+2>bj=t+1. 因(t+1)γ minAsj=asj=t+2≤minBj. 子情形2.2bj+1=bj+1.设存在bj 则显然(as2,…,asj-1,asj,…,asm,…,ask)⊆im(t)且1 minAsi=asi=bi≤minBi, 当j≤i≤m,显然asi=bi+1>bi.又因(t+1)γ minAsj=asj=bj+1=t+2≤minBj, 又t+2≤minBj minAsj+2≤minBj+2, ⋮ minAsm≤minBm. 综上所述,根据引理1,γ满足条件(1)、(2)和(3),故γ∈CntCn,即γ∈Ωt,从而Y⊆Ωt.因此 Ωt={α∈Cn|(t+1)α □ 证明由引理2知, Ωt={α∈Cn|(t+1)α (t+1)βγ=(t+1)γ=t+1. 故βγ∈Wt,从而Wt是子半群. □ 引理4任取k1,k2,…,kj∈E′n-1,其中j∈{1,2,…,n-1}且k1 Mk1,k2,…,kj=Ωk1∪Ωk2∪…∪Ωkj, 则CnMk1,k2,…,kj为子半群. 证明令Wr=CnΩkr(r=1,…,j),则显然 CnMk1,k2,…,kj=Cn(Ωk1∪Ωk2∪…∪Ωkj)=W1∩W2∩…∩Wj. 由引理3知,每一个Wr(r=1,…,j)为子半群,故W1∩W2∩…∩Wj为子半群,得证. □ 设φ为Cn的秩2自同态,在本文中令 引理5(e0)φ≠(ιn)φ. 证明假设(e0)φ=(ιn)φ.对任意的α∈Cn,则有 (α)φ=(αιn)φ=(α)φ(ιn)φ=(α)φ(e0)φ=(αe0)φ=(e0)φ. 故|(Cn)φ|=1,与φ为Cn的秩2自同态矛盾,引理得证. □ 引理6(f0)φ-1={g∈Cn|(g)φ=f0}是Cn的一个理想. 证明任取α,β∈Cn,g∈(f0)φ-1,则 (αgβ)φ=(α)φf0(β)φ=(α)φ(e0)φ(β)φ=(αe0β)φ=f0. 故αgβ∈(f0)φ-1,因此(f0)φ-1是Cn的一个理想. □ 故(Cn)φ=f1.从而|(Cn)φ|=1,矛盾.因此引理得证. □ α=η1η2…ηi, 从而 (α)φ=(η1η2…ηi)φ=(η1)φ(η1)φ…(ηi)φ=f1. 这与(α)φ=f0矛盾,故引理得证. □ 引理9设(f0)φ-1∩E′n-1={l1,l2,…,lp},其中p∈{1,2,…,n-1}且l1 (f0)φ-1=Ωl1∪Ωl2∪…∪Ωlp. 证明由引理6知,显然Ωl1∪Ωl2∪…∪Ωlp⊆(f0)φ-1. 反之,若(f0)φ-1Ωl1∪Ωl2∪…∪Ωlp,则存在μ∈(f0)φ-1但μ∉Ωl1∪Ωl2∪…∪Ωlp. Ωls={α∈Cn|(ls+1)α 因μ∉Ωl1∪Ωl2∪…∪Ωlp,故对每一个s(s=1,…,p),有μ∉Ωls,从而 (ls+1)μ=ls+1. 由[4,定理14.4.5]知存在r(2≤r≤n-1)个互不相同的幂等元ν1,ν2,…,νr∈E′n-1,使得 μ=ν1ν2…νr. 故任取s∈{1,…,p},对每一个j(j=1,…,r),有 (ls+1)νj=ls+1. 显然νj∉(f0)φ-1∩E′n-1,故νj∉(f0)φ-1,从而νj∈(f1)φ-1(j=1,…,r).于是μ∈(f1)φ-1,矛盾.因此(f0)φ-1⊆Ωl1∪Ωl2∪…∪Ωls. 综上, (f0)φ-1=Ωl1∪Ωl2∪…∪Ωls. □ c1: 若α,β∈Mk1,k2,…,kj,由定义知Mk1,k2,…,kj是一个理想,故αβ∈Mk1,k2,…,kj,从而 c2: 若α,β∉Mk1,k2,…,kj,则由引理4知αβ∉Mk1,k2,…,kj,故 c3: 若α∈Mk1,k2,…,kj,β∉Mk1,k2,…,kj,则αβ∈Mk1,k2,…,kj,故 c4: 若α∉Mk1,k2,…,kj,β∈Mk1,k2,…,kj,同理αβ∈Mk1,k2,…,kj,则 因e0ιn=ιne0=e0,故 h1h2=h2h1=h1. 又由引理8知(h1)σ-1∩E′n-1≠φ,不妨设 (h1)σ-1∩E′n-1={z1,z2,…,zq}, 其中q∈{1,2,…,n-1}且z1 (h1)σ-1=Ωz1∪Ωz2∪…∪Ωzq, 即(h1)σ-1=Mz1,z2,…,zq.根据定义,因此 □ 定理2的证明对任意的φ∈G,由定理1知存在不同的幂等元h1,h2和理想Mz1,z2,…,zq,使得 且φ由h1,h2,Mz1,z2,…,zq决定.因此G的元素个数由理想Mz1,z2,…,zq的个数和幂等元对(h1,h2) 的个数决定. □ 注通过本文的结果,我们提出下面一个问题:刻画Cn的秩不为2的所有自同态.

1 主要结果的证明