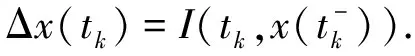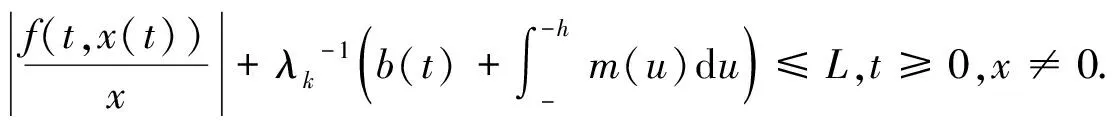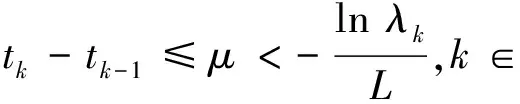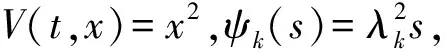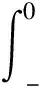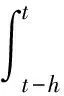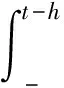无限时滞脉冲泛函微分方程的有界性
2023-02-11陈成军申建华
陈成军,申建华
(杭州师范大学数学学院,杭州 浙江 311121)
0 引言和预备知识
脉冲微分方程的理论可以追溯到Mil’man和Myshkis[1]的工作.这个理论现在不仅被认为比相应的无脉冲微分方程理论更为丰富,而且为许多现实世界现象的数学建模提供了一个更为自然的框架.过去一些年,脉冲微分方程理论研究取得重大进展,例如,参见[2—10]和其中所引用的文献,脉冲泛函微分方程理论也已得到充分的发展.
本文中,我们将讨论具有无限时滞的Volterra型泛函微分方程
x′(t)=F(t,x(·)),
(1)
在非线性脉冲条件

(2)
扰动下的有界性,其中x′(t)表示x(t)的右导数,t* 令J⊂是任意区间,定义 PC(J,n)={x:J→n|x在除脉冲点t=tk∈J外都连续,和存在,且 对∀t≥t*,将PC([α,t],n)记作PC(t),定义 PCB(t)={x∈PC(t)|x有界}. 对∀φ∈PCB(t),定义φ的范数为: 对∀t≥t*,H>0,令 PCBH(t)={φ∈PCB(t)|||φ|| 对某个给定的σ≥α及φ∈PCB(σ),我们给出方程(1)-(2)的初值条件为: x(t)=φ(t),α≤t≤σ. (3) 定义1x(t)被称作初值问题(1)-(3)关于σ的解,如果 x:[α,β)→n(其中t*<β≤∞)在t∈[α,β){tk,k=1,2,…}上是连续的,和存在,且满足(1)-(3). 我们假定下述(H1)-(H4)成立,则初值问题(1)-(3)的解x(t,σ,φ)存在且唯一[9]. (H2)F在每个紧集PCB(t)上关于φ是局部Lipschitz的,即对∀γ∈[α,β)及每一个紧集G⊂PCB(t),总存在一个常数L=L(γ,G),使得 |F(t,φ(·))-F(t,ψ(·))|≤L||φ-ψ||[α,t], 其中,t∈[α,γ]以及φ,ψ∈G. (H3)I(t,x)∈C([t*,∞)×n,n),且对∀ρ>0,总存在一个ρ1>0(0<ρ1<ρ),使得对∀k∈+,当x∈S(ρ1)时,我们有x+I(tk,x)∈S(ρ). (H4) 对∀x(t)∈PC([t*,∞),n),有F(t,x(·))∈PC([t*,∞),n). 定义2脉冲泛函微分方程(1)-(2)的解被称作是: (S1)一致有界的,若对任意实数B1,存在B2>0,使得当t≥σ(σ≥t0),且 ||φ||≤B1时,有 |x(t,σ,φ)|≤B2成立. (S2)一致最终有界的,若对任意实数B3>0,存在T>0,和B>0,使得当t≥σ+T(σ≥t0),且||φ||≤B3时,有|x(t,σ,φ)|≤B成立. 定义3函数V:[α,∞)×S(ρ)→+属于集合v0,如果 (A1)V在每个集合[tk-1,tk)×S(ρ)上连续,且对所有的x∈S(ρ)和k∈+,极限 (A2)V关于x是局部Lipschitz的,且有V(t,0)≡0成立. 我们假设F(t,0)≡0,和I(tk,0)≡0,以便方程(1)-(3)存在零解x(t)≡0.同样,在本文中,我们将假设β=∞.更确切的说,我们将只考虑能从σ的右边拓展到∞的方程(1)-(2)的解x(t,σ,φ). 定义本文中可能用到的函数集合: K={g∈C(+,+)|g严格单调递增且g(0)=0}. K1={g∈C(+,+)|g(0)=0,且当s>0时,g(s)>0}. K2={g∈C(+,+)|g(0)=0,当s>0时,g(s)>0,且g非减}. 定理1设存在常数U>0,及φ1,φ2∈K,C∈K1,p∈PC(+,使得下列条件成立: V(t,x(t))>ψ(V(s,x(s))),max{α,t-h}≤s≤t 时,有不等式 V′(t,x(t))≤p(t)C(V(t)) 成立,其中对∀k,都有ψ(s)≤ψk(s),x(t)=x(t,σ,φ) 是方程(1)-(2)的任意解; 则方程(1)-(2)的解一致有界且一致最终有界. 证明给定B1≥U,满足对∀σ≥t*,φ∈PCBB1(σ).取正数B2≤ρ1,使得对∀k,有 φ2(B1)≤ψk(φ1(B2)). 令x(t)=x(t,σ,φ)是方程(1)-(2)的任意解,记V(t)=V(t,x(t)).对某个m∈+,令σ∈[tm-1,tm),其中t*=t0,则当α≤t≤σ时,我们有: φ1(|x(t)|)≤V(t)≤φ2(B1)≤ψk(φ1(B2))<φ1(B2). (4) 即: |x(t)| 现我们断言: |x(t)|≤B2,t∈[σ,∞). (5) 如果式(5)不成立,则假设∃t∈[σ,∞),使得|x(t)|>B2. 定义 矛盾! 定义 因为 另一方面,由 φ2(B1)≤ψm-1(φ1(B2))≤V(t)≤φ2(|x(t)|) 将此不等式积分可知: 矛盾! 与情况1证明类似,定义 我们下证方程(1)—(2)的解一致最终有界.令 由上述证明知方程(1)—(2)的解一致有界,故对给定的∀B3≥U,我们总能找到一个B4>B,且B4≥ρ1,使得当φ∈PCBB3(σ)时有 |x(t)|≤B4,V(t)≤φ1(B4),t≥α. 下面我们将证: ∃T>0,使得当φ∈PCBB3(σ)时,有|x(t)|≤B,t≥σ+T. 因为当φ1(B)≤u≤φ2(B4)时有不等式ψ(φ1(B))≤ψk(φ1(B))≤ψk(u) (6) 所以有 我们取d=d(B),使得0 ψ(u)≤ψk(u)≤u-M2/M 令N是使得φ2(B4)≤φ1(B)+Nd成立的第一个正整数.再令 T=τ+(h+τ)(N-1), 我们将证: |x(t)|≤B,t≥σ+T. 为此,我们定义m1=m,及 mi=inf{k∈Z+|tk≥tmi-1+h},i=2,3,…,N. 则我们知:tm1=tm≤tm+σ-tm-1≤σ+τ.又由定义tm2≤tm1+h+τ. 不失一般性的,我们设 tmi≤tmi-1+h+τ,i=2,3,…,N. 特别地,当i=N时,我们有 tmN≤σ+τ+(N-1)(h+τ)=σ+T. 现我们证明: V(t)≤φ2(B4)-id,t≥tmi,i=1,2,…,N. (7)i 先证(7)i成立.反设存在某个t≥tm1=tm,使得V(t)>φ2(B4)-d.定义 ψk(φ2(B4))<φ2(B4)-d. 又当t≥σ时,有V(t)≤φ2(B4),所以 再定义 因为 综上所述,我们有 因此 V(t)≥ψk(φ2(B4))>ψk(φ2(B))>ψk(φ1(B))=φ2(U). 将此不等式积分可得: (8) 又因为 (9) 且显然有φ1(B)≤φ2(B4),所以 ψk(φ1(B))≤ψk(φ2(B4))<φ2(B4)-d<φ2(B4). 从而再由φ2(B4)-d≤s≤φ2(B4)及M的定义知, 1/C(s)≤M.结合式(9),我们有 这显然与式(8)矛盾! 故原假设不成立,从而(7)i成立. 假设对每个1≤i V(t)≤φ2(B4)-(i+1)d,t≥tmi+1. (7)i+1 反设存在某个t≥tmi+1,使得:V(t)>φ2(B4)-(i+1)d.定义 ψk(φ2(B4)-id)<φ2(B4)-id-d=φ2(B4)-(i+1)d, 从而 因为 V(t)≥ψk(φ2(B4)-id). 因此,我们有 再由不等式tmi+1≥tm+h,知tmi≤tmi+1-h知 另一方面,由 φ2(|x(t)|)≥V(t)≥ψk(φ2(B4)-id)≥ψk(φ1(B))>ψ(φ1(B))=φ2(U) 将此不等式积分可得 (10) 再由M2与M定义知 矛盾! 故原假设不成立,即(7)i+1成立. 由简单归纳可知,对∀i=1,2,…,N,(7)i都成立.特别地,令i=N,我们有 φ1(|x(t)|)≤V(t)≤φ2(B4)-Nd≤φ1(B),t≥σ+T≥tmN. 所以|x(t)|≤B,t≥σ+T. 综上所述,当t≥σ+T时,有|x(t)|≤B,即方程(1)-(2)的解一致最终有界.定理证毕. 定理2设存在常数U>0,及φ1,φ2∈K,C∈K1,p∈PC(+,使得: V(t,x(t))>ψ(V(s,x(s))),α≤s≤t 时,有不等式 V′(t,x(t))≤p(t)C(V(t)) 成立.其中对∀k,都有ψ(s)≤ψk(s),x(t)=x(t,σ,φ) 是方程(1)-(2)的任意解; 则方程(1)-(2)的解一致有界. 例考虑方程 (11) (12) 其中,τ>0,f∈C(+,+,+)).g(t,u,v)在+×(-∞,0]×上是连续的,且|g(t,u,v)|≤m(u)|v|,对x∈,有|x+I(tk,x)|≤λk|x|,其中λk∈(0,1)(k∈+). 假设存在一个常数L>0,及h>0,使得 (13) 假设存在一个常数μ>0,使得 (14) 则方程(11)-(12)的解一致有界且一致最终有界. 证明首先由(13)—(14)我们可以找到一个常数A>0,使得 对∀x(t)=x(t,σ,φ),有 故我们有 V′(t,x(·))≤2x(t)f(t,x(t))+2b(t)|x(t)||x(t-τ)|+ 2L|x(t)|2. 记p(t)=2L,C(s)=s.则有V′(t,x(·))≤p(t)C(V(t)). 此外,我们还有 则根据定理2知:方程(11)—(12)的解一致有界. 更进一步,对任意解x(t),若满足||x(t)||(-∞,t]≤1及 ψk(V(s,x(s))) 则我们有 V′(t,x(·))≤2x(t)f(t,x(t))+2b(t)|x(t)||x(t-τ)|+ 且 再由定理1知:方程(11)-(12)的解一致有界且一致最终有界.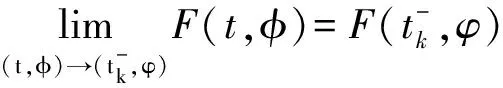
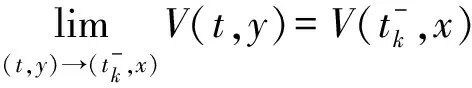
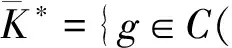
1 主要结果


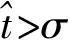
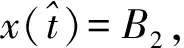


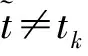
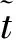
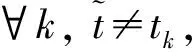
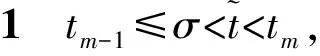
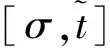

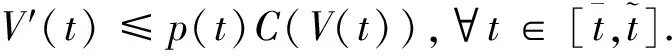
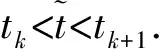
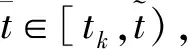
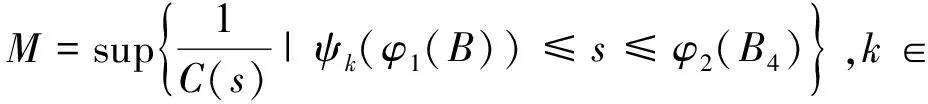
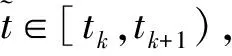

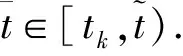


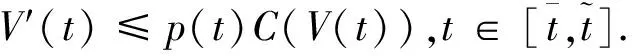
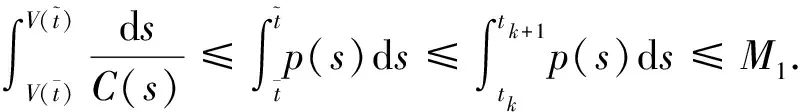
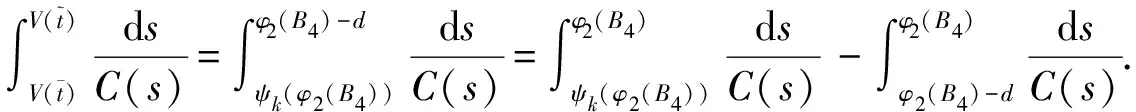
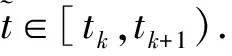

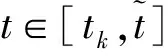
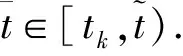

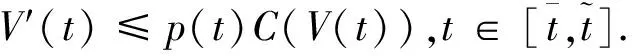
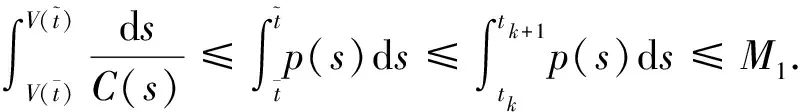


2 应用举例