空间波数混合域三维各向异性强磁性介质磁场数值模拟
2023-02-11戴世坤张莹凌嘉宣陈轻蕊贾金荣冉应强
戴世坤,张莹*,凌嘉宣,陈轻蕊,贾金荣,冉应强
1 中南大学有色金属成矿预测与地质环境监测教育部重点实验室,长沙 410083 2 中南大学地球科学与信息物理学院,长沙 410083
0 引言
磁性体感应磁化产生与磁化场方向相反的磁场,造成磁性体内部磁化场减小的现象称为自退磁效应.弱磁性体磁化率不超过0.1 SI,其自退磁效应可忽略不计;强磁性体磁化率大于0.1 SI,其自退磁效应导致感应磁化方向明显偏离外部地磁场,磁异常幅值减小,形态畸变(张拴宏和周显强,1999;Guo et al.,2001; Austin et al.,2014).强磁性矿物受构造应力作用产生定向排列、韧性变形或动态重结晶,表现出各向异性,其自退磁效应更加复杂,必须充分考虑其影响(余钦范,1983;吴汉宁,1988;Kaufman,1992;管志宁,2005;贾志业等,2020;华天等,2021;胡智龙等,2022).因此研究各向异性条件下强磁性体磁场响应特征,对于寻找石油、天然气、有用矿产资源,研究深部区域、全球地质构造、地震预报和监测,解决环境、工程、灾害等一系列地质问题具有重要意义(王书惠,1981,1983;李媛媛等,2010;张志厚等,2021).
强磁性体磁场数值模拟最早是研究各向同性介质磁化率磁场的响应,Vogel(1963)提出用向量级数表示磁体内部各体积元有效磁化强度,并使用逐次逼近求解,计算强磁性体时向量级数收敛很慢甚至发散,且计算效率低;Eskola 和 Tervo(1980)考虑退磁效应,采用面积分方法进行计算,用磁性体表面磁场分量表示磁性体磁场,若磁性体边界不平滑,结果会有误差;Furness(1999)改进面积分方法,在磁性体表面放置偶层计算磁场,考虑剩磁和退磁,计算均匀磁化的任意三维磁性体,对难以产生稳定数值解的薄层地质体仍能得到精确解,当计算点距离离散表面小于一个单位元长度时,计算结果偏差较大;Purss和Cull(2005)通过由均匀任意直径球形体素定义的分段模型,在迭代基础上计算高磁化率磁性体磁场,但磁化率较高时会有误差;Ouyang 和Chen(2020)运用积分方程和高斯FFT,对磁性体进行棱柱剖分,实现各向同性强磁体磁场数值模拟.
随着研究的深入,越来越多人认识到各向异性强磁性体磁场数值模拟的重要性,王书惠(1983)给出考虑磁各向同性与退磁效应的磁法勘探正问题有限元解法,但仅研究二度体问题;余钦范和陈德怀(1986)给出层状结构磁各向异性体磁场计算方法,同时考虑退磁效应;吴燕冈等(2001)在王书惠(1983)研究基础上,采用差分数值解法求解强磁各向异性正问题,由二维发展到三维;付文祥(2011)基于积分方程法计算任意形状二度体强磁介质磁异常,采用三角棱柱单元拟合任意形状多边形,对内存需求较高;Takahashi 和 Oliveira(2017)给出各向同性和各向异性椭球体磁场的解析公式,同时考虑自退磁效应.这些各向异性强磁性体数值模拟方法有效地提升了数值模拟的精度和速度,但这些基于有限元、有限差分和积分方程的方法对于大规模复杂条件下三维各向异性强磁性介质数值模拟需要更精细的剖分,内存需求更高,影响其计算效率,限制了其大规模的应用.
为此,本文提出一种适用于各向异性强磁性体磁场的高效高精度数值模拟方法.该方法通过对各向异性强磁性体磁位满足的三维偏微分方程进行水平方向二维傅里叶变换,降为不同波数之间相互独立的一维常微分方程,计算量减少,存储需求降低,具有高度并行性;保留垂直方向为空间域,可根据实际情况调整单元疏密程度,能兼顾计算精度和计算效率;最后采用迭代法求解场值,对于任意各向异性介质强磁性体模型均能稳定收敛,实现任意各向异性强磁性体磁场的三维高效、高精度数值模拟.
1 理论和方法
1.1 磁化率各向异性
当磁性体磁化率为各向同性时,介质沿不同方向具有相同磁化率,用标量描述;当介质磁化率为各向异性时,磁化率为张量表达式为:
(1)
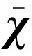
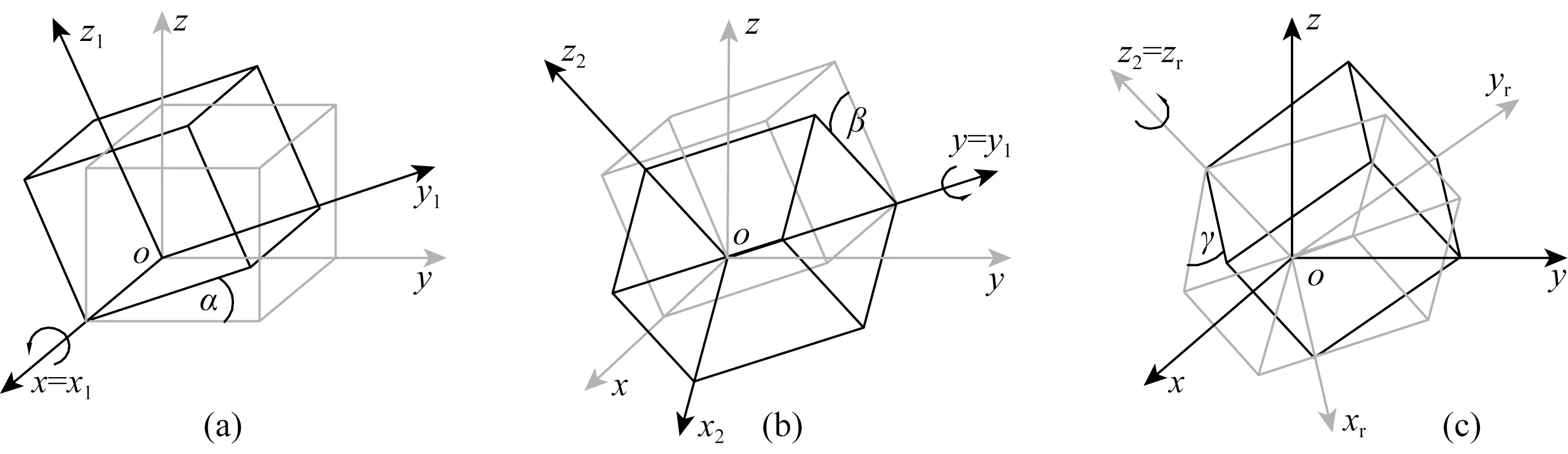
图1 坐标系旋转示意图
图1中(a)为绕x轴旋转α角度,(b)表示在(a)基础上绕y轴旋转β角度,(c)表示在图(b)基础上绕z轴旋转γ角度.坐标系中点的坐标变化(x,y,z)→(xr,yr,zr)转换过程如式(2):
(2)
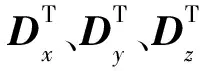
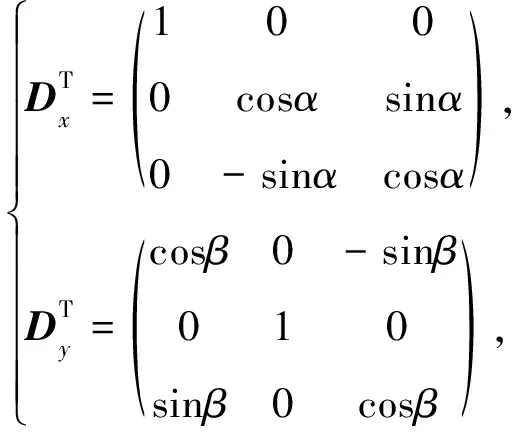
(3)
(3′)
(4)
(5)
其中:
(6)
(7)
1.2 空间波数域磁位控制方程
磁异常场磁位Ua与磁化强度M在空间域满足三维偏微分方程(Blakely,1995):
(8)
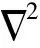
磁化强度M可表示为:
(9)
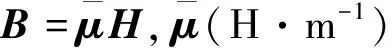
空间域背景场磁场强度H0三个方向分量分别表示为H0x、H0y、H0z(Takahashi and Oliveira,2017):
(10)
式中,‖H0‖表示背景场H0的L2范数,I为目标区域磁倾角,D为目标区域磁偏角.
对式(8)进行水平方向二维傅里叶变换,得到空间波数域异常磁位满足的一维常微分方程:
(11)
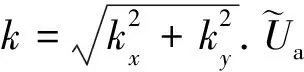
1.3 边界条件
对常微分方程式(11)进行求解,需给出合适的边界条件,边界条件示意图如图2所示.
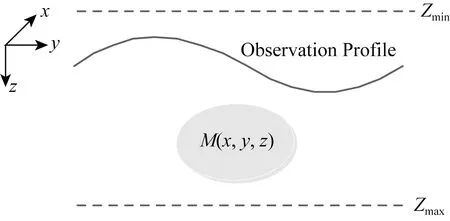
图2 笛卡尔坐标系中边界条件示意图
式(11)中只有上下边界条件,取边界为无源区域.在笛卡尔坐标系中,取z轴向下为正,设上边界为Zmin,下边界Zmax.
此时边界上空间-波数域异常磁位满足空间-波数域拉普拉斯方程:
(12)
(13)
式中,A、B为任意常数.
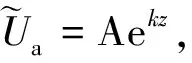
(14)
(15)
1.4 边值问题有限元求解
由式(11)以及边界条件式(14)和(15)可得空间-波数混合域异常磁位满足的边值问题为:
(16)
运用变分法(徐世浙,1994),可得与边值问题(16)等价的变分问题(推导过程详见附录A):
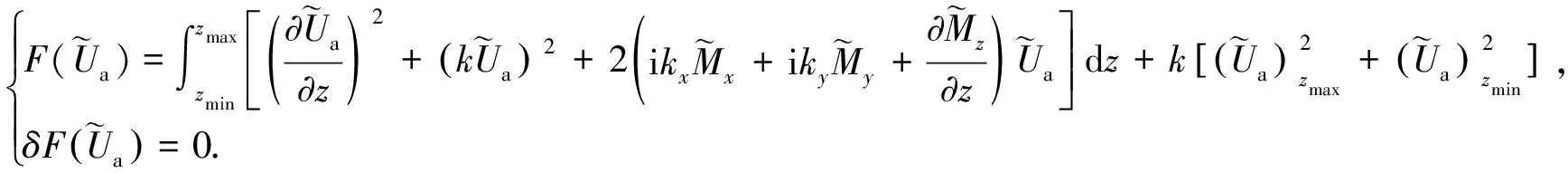
(17)
在图2所示笛卡尔坐标系中,沿z方向进行单元离散,可根据实际情况灵活调整每个单元的间隔大小,每个单元内采用二次插值,逐项进行单元分析、总体合成(见附录B),可得由全体节点组成的总体矩阵:
(18)
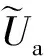
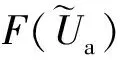
(19)
而δuT≠0,因此:
Ku=P,
(20)
式中,K是五对角矩阵,P是源项,u为待求空间波数域异常磁位.
采用追赶法(Boisvert,1991)求解式(20)的五对角方程组,可求得不同波数下的空间-波数域异常磁位.
1.5 磁异常场计算
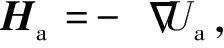
(21)
(22)
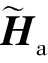
总强度磁异常ΔT由式(23)给出(Blakely,1995):
ΔT=‖B0+Ba‖-‖B0‖,
(23)
B0表示背景场磁感应强度,Ba表示异常场磁感应强度.
1.6 迭代算法
根据式(8)、(9),可得空间域异常磁位、背景场强度和异常场强度满足的微分方程为:
(24)
式中H=H0+Ha,弱磁性体产生的异常场Ha通常忽略不计,认为Ha为0,直接求解式(24)可得精确解;强磁性体异常场Ha不可忽略,式(24)不能直接求解,本文采用迭代法进行求解.
Pankratov等(1997)、Ouyang和Chen(2020)基于电磁场计算里的修正Born级数(Singer,1995; Pankratov et al.,1997; Zhdanov and Fang,1997; Hursán and Zhdanov,2002; Gao and Torres-Verdín,2006),采用积分方程法,构造了能使得各向同性介质强磁场迭代计算稳定收敛的格式.在此基础上,本文利用微分方程与积分方程求解的等效性,构造了各向异性介质强磁场稳定收敛的迭代格式,表达式为:
(25)
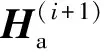
2 算法流程
空间-波数混合域三维各向异性强磁性介质磁场数值模拟算法流程如下:
(1)模型剖分:水平x、y方向根据目标区域空间范围均匀剖分,垂直z方向剖分可依据异常体分布进行适当加密和稀疏,网格剖分如图3所示.
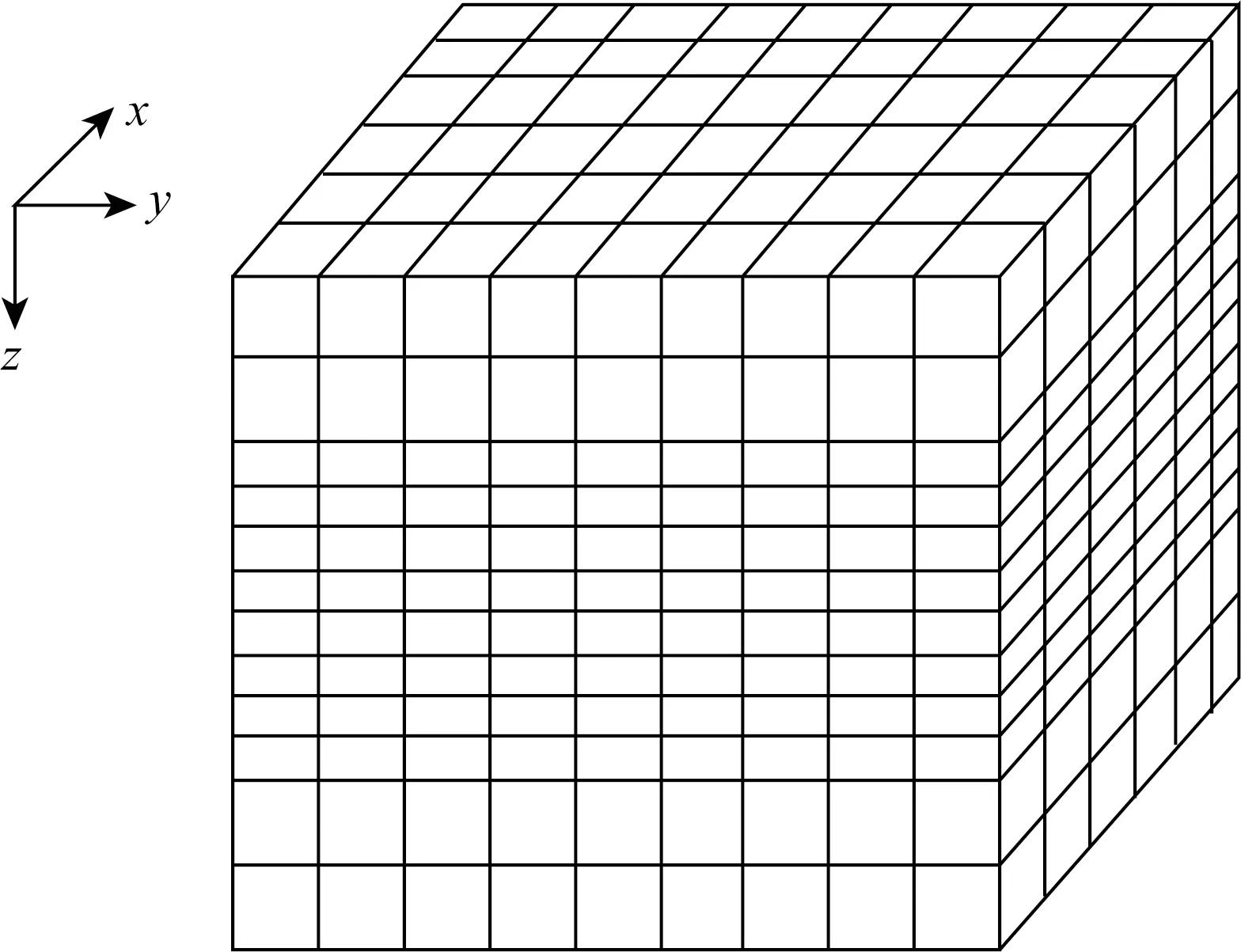
图3 网格剖分示意图
(2)磁化强度计算:给定背景场、各向异性介质磁化率等参数,求得空间域磁化强度,对磁化强度沿x、y方向进行二维傅里叶变换,将其转换到空间波数域.
(3)一维有限元求解:对空间波数域异常磁位满足的边值问题运用一维有限元法求解,得到空间波数域异常磁位,依据异常磁位与磁异常场在空间波数域关系,求得空间波数域异常场强度.
(4)空间域磁异常场计算:对空间波数域磁异常场进行二维傅里叶反变换,计算得空间域磁异常场.
(5)空间域紧算子迭代计算:将本次迭代计算的磁异常场与上次迭代计算的磁异常场进行比较,满足迭代终止条件时,迭代结束并输出计算结果,否则将此次计算的总场代入步骤(2)中重复计算直到满足迭代终止条件.
本文采用算法迭代终止条件为:
(26)
∑|H(i+1)|表示每个节点第i+1次迭代计算所得总场绝对值之和,∑|Hi|表示每个节点第i次迭代计算所得总场绝对值之和.迭代计算具体流程图如图4所示.
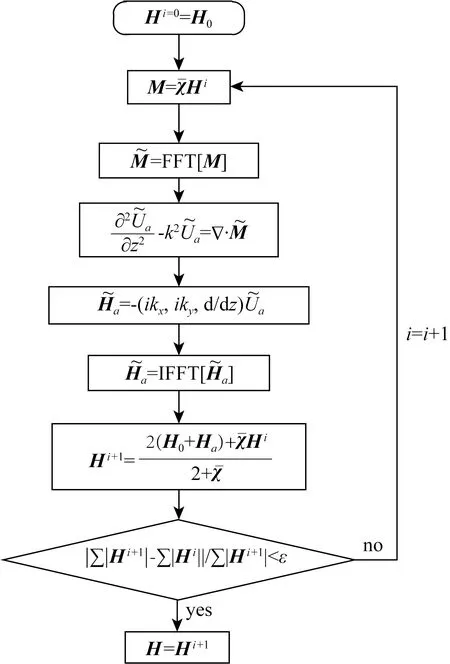
图4 迭代计算算法流程
3 算法验证
本文算法均采用Fortran95语言进行编写,开发平台为Windows系统下Visual Studio 2019,采用编译器为IVF 2020.测试机型为intel i9,Core 3.0 GHz,内存128 G.测试算例中傅里叶变换算法程均采用Gauss-FFT(Wu and Tian,2014)实现,迭代终止条件ε=10-4.
3.1 正确性验证
为验证算法正确性,设计椭球体模型与解析解(Takahashi and Oliveira,2017)进行对比.模拟区域范围为1000 m×1000 m×1000 m,节点个数为401×401×401.背景磁场强度50000 nT,磁倾角58.3°,磁偏角45°,椭球体中心坐标为(500 m,500 m,300 m),三轴半径分别为180 m,170 m,160 m,计算区域及模型示意图如图5所示,剖面图如图6所示.椭球主轴磁化率分别为20 SI、10 SI、5 SI,旋转欧拉角分别为90°、60°、10°.
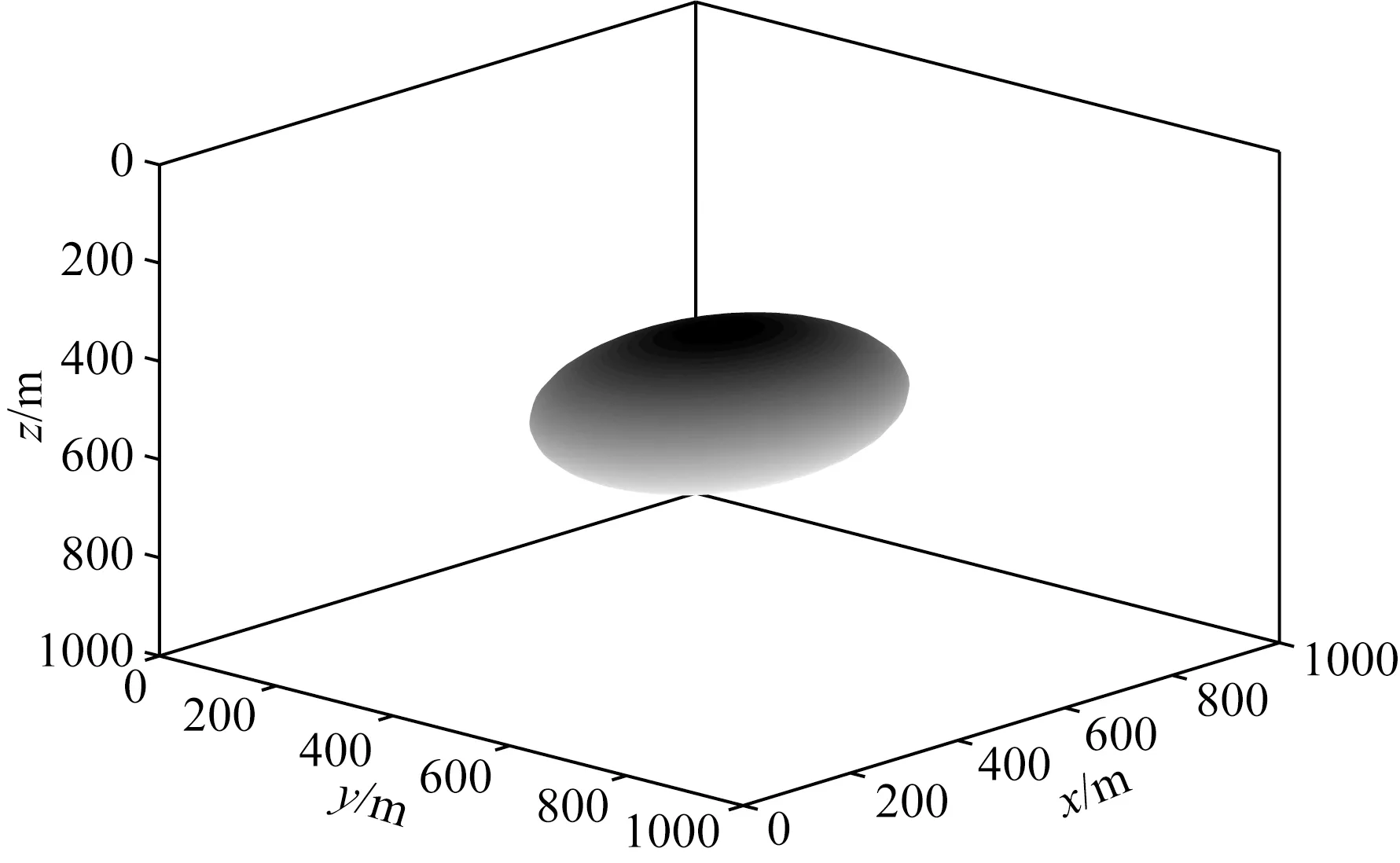
图5 计算区域及模型示意图
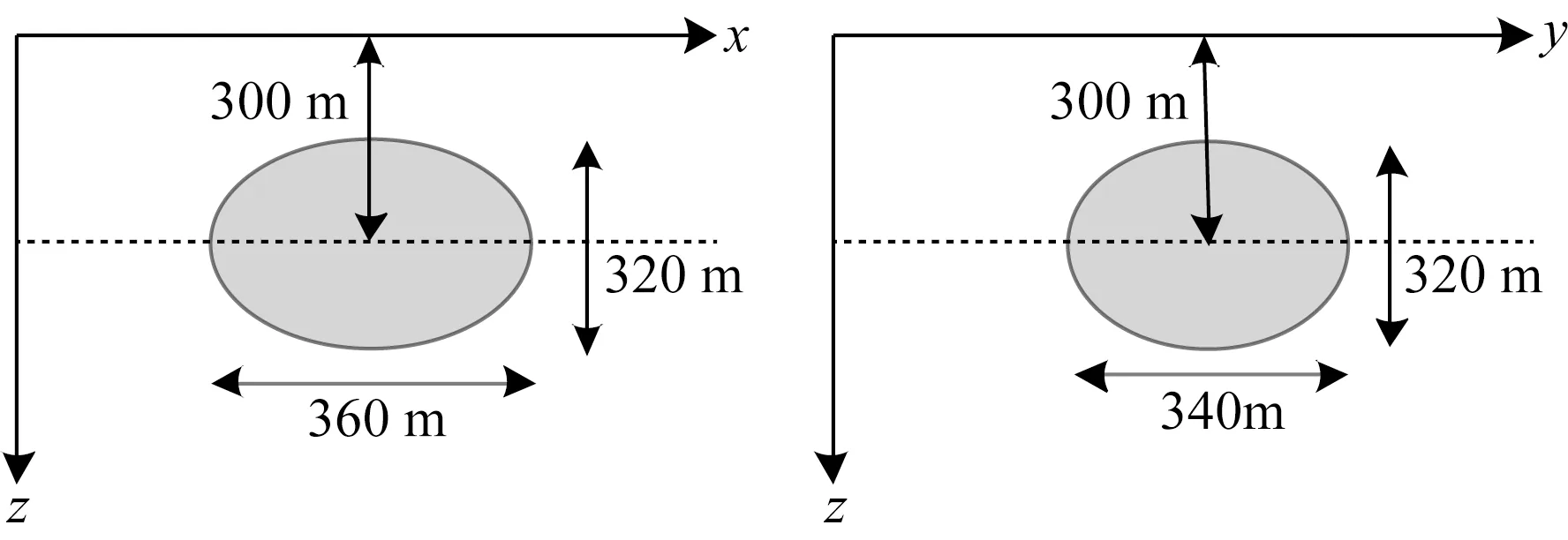
图6 模型剖面图
模型总强度磁异常ΔT以及三个分量Bax、Bay、Baz分量在z=0 m平面数值解、解析解和绝对误差如图7所示.模型异常场数值解与解析解基本吻合,其绝对误差与解析解相比均低两个数量级以上.模型经13次迭代计算后ΔT、Bax、Bay、Baz相对均方根误差分别为0.79%、0.83%、0.81%、0.78%.
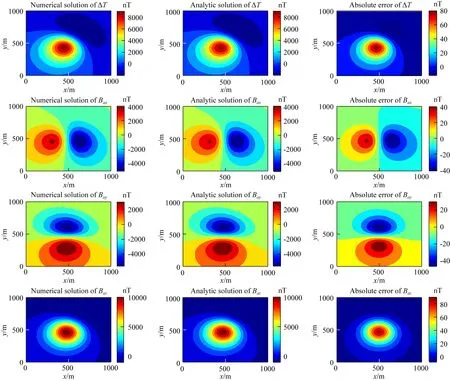
图7 模型数值解、解析解及误差对比
3.2 收敛性验证
采用3.1节中模型,分别改变磁化率主轴分量和欧拉角,分析各向异性参数对算法收敛性影响.
(1)分析单轴各向异性介质中磁化率主轴z分量对收敛性影响,欧拉角都为0°,令磁化率主轴分量1、2不变,改变主轴分量3,迭代次数如表1所示.由表1可知,主轴分量1、2不变,3越大,迭代收敛次数越多,但算法均稳定收敛.仅改变主轴分量1或2,也可得到相同结论.
表1 单轴各向异性介质不同3迭代次数
Table 1 Statistics of iteration times of different 3 in uniaxial anisotropy

表1 单轴各向异性介质不同3迭代次数
-(SI)1/1/11/1/101/1/501/1/2001/1/5001/1/1000Iterations612244879122
(2)分析三轴各向异性介质中欧拉角对收敛性影响,令主轴分量1、2、3不变,欧拉角α、β为0°,改变γ角度,迭代次数如表2所示.由表2可知,不同欧拉角γ未改变zz数值,但最终磁化率张量值发生改变,进而算法迭代次数发生变化.

表2 三轴各向异性不同γ迭代次数统计
综上,磁化率主轴分量和欧拉角变化均对算法收敛性有影响,本质上是因为磁化率主轴分量和欧拉角改变了最终磁化率张量数值,从而影响迭代收敛性.此外,对于磁化率任意各向异性,算法均在有限次数内收敛.
4 效率对比
COMSOL Multiphysics是一款商业化有限元仿真软件,运用其AC/DC模块进行各向异性介质强磁场数值模拟,对比本文算法与有限元算法效率.
模型计算区域为1000 m×1000 m×1000 m,磁异常体为边长400 m的正方体,且位于计算区域中心,如图8所示.背景磁场强度50000 nT,磁倾角58.3°,磁偏角30°.磁异常体磁化率张量为[2 SI,2 SI,1 SI],欧拉角都为0°.COMSOL有限元算法与本文算法均采用16线程并行.

图8 正方体磁异常模型示意图
采用六面体剖分,在相同剖分条件下,本文算法与COMSOL有限元算法内存消耗与时间占用情况如表3所示.对应曲线变化图如图9所示,结合图表可知,随着网格数增多,两种算法的计算时间和内存占用均增多,其中本文算法耗时和内存需求随节点数增多呈线性变化.当节点数为101×101×101时,本文算法所需内存为2 GB,迭代计算时间为22.3 s,COMSOL算法所需内存为19.32 GB,时间为94 s,本文算法速度快3倍,内存占用少9倍;当节点数为201×201×201时,COMSOL有限元算法占用计算机内存128 G,本文算法仅占用内存15.8 G,说明本文算法在相同计算机配置下能够适用更大规模节点数的计算,计算规模越大,本文算法优势越明显.
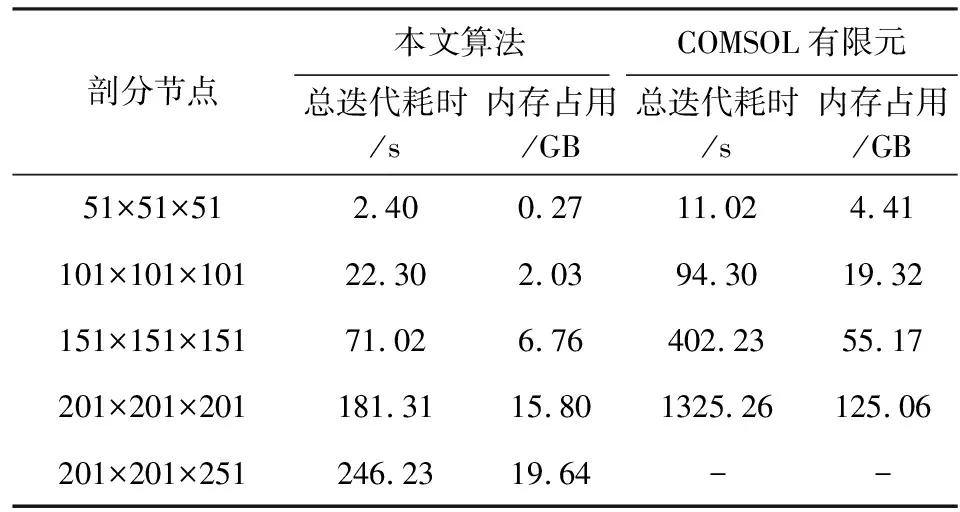
表3 本文算法与COMSOL有限元算法迭代耗时与内存占用统计
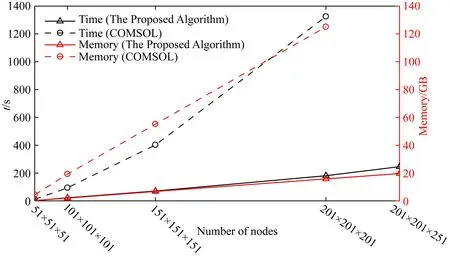
图9 本文算法与COMSOL有限元算法内存消耗与时间占用随剖分节点数变化趋势
5 各向异性响应分析
强磁性磁铁矿多成层状结构,具有各向异性特征.采用图8中正方体异常模型,分别设计不同磁化率大小的水平层理介质(VTI)、垂直层理介质(HTI)和倾斜层理介质(TTI)模拟各向异性磁铁矿赋存状态,研究各向异性强磁性介质对磁场形态和幅值影响.其中VTI介质和HTI介质仅改变主轴参数,TTI介质仅改变角度.背景场以及计算模型与第4节中模型一致,剖分节点个数为201×201×201.
5.1 VTI介质
图10 VTI介质示意图
z=0 m平面VTI介质不同3磁异常场响应如图11所示,y=500 m测线异常场场值变化曲线如图12所示.综合图11和图12,3从0.01 SI变化至100 SI,跨越四个数量级,ΔT、Bax、Bay、Baz四个分量幅值和形态均有较大变化.3越大,异常场幅值越大,场值越强.3从0.01 SI变化至0.1 SI时,场值形态和幅值接近,变化小;3从0.1 SI变化至1 SI时,场值形态发生明显变化,数值增大明显;3从1 SI变化至100 SI时,场值变化快,且幅值越来越大.
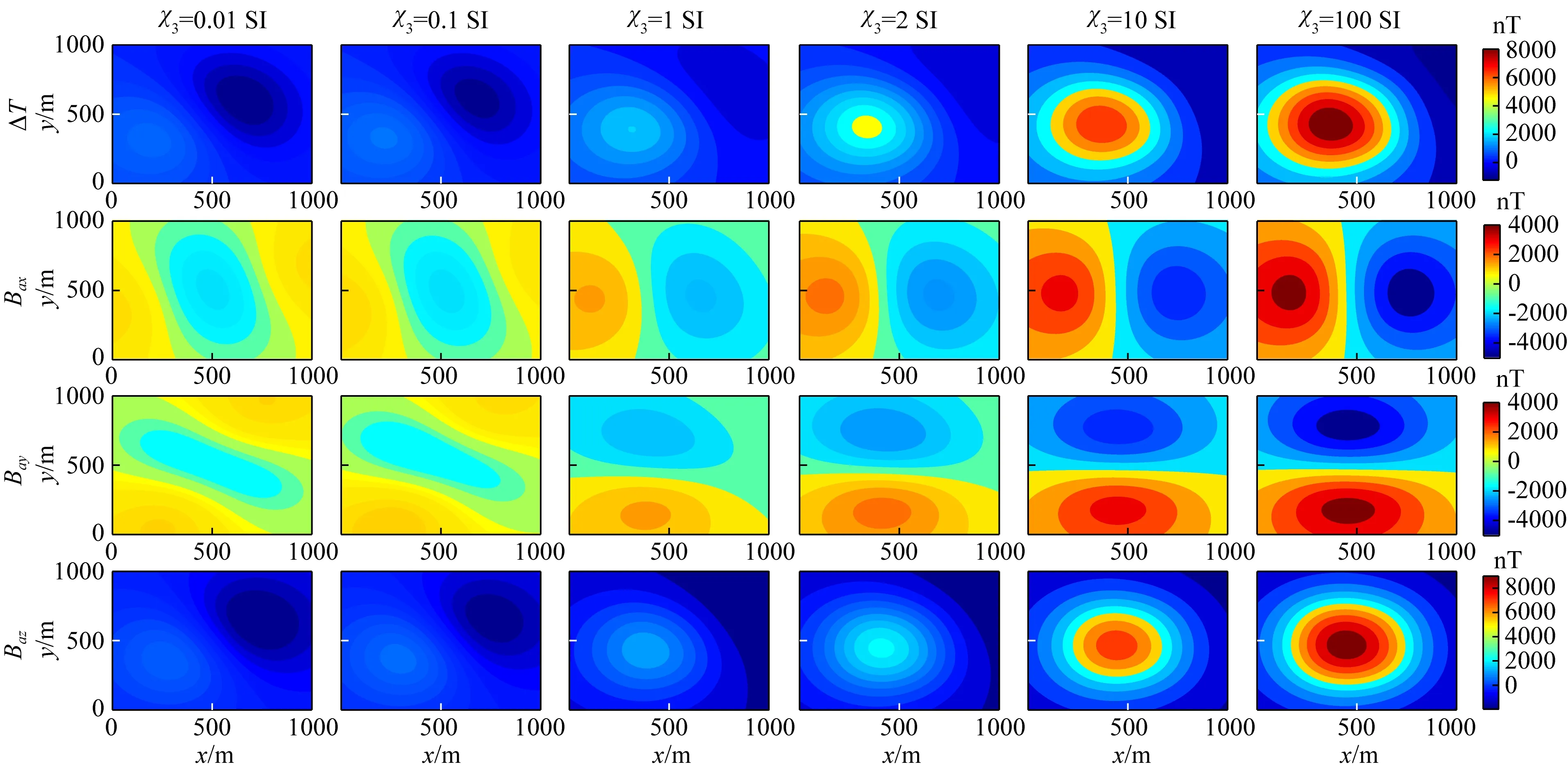
图11 VTI介质不同3 磁异常场响应(z=0 m平面)
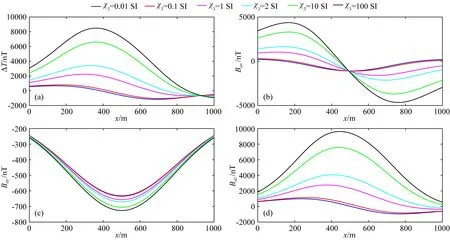
图12 VTI介质不同3磁异常场曲线(y=500 m)
5.2 HTI介质
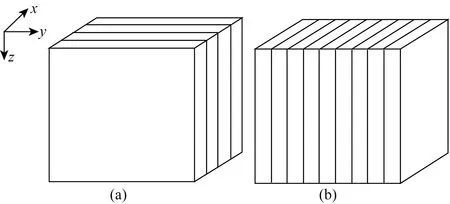
图13 HTI介质示意图
z=0 m平面HTI-X介质不同1磁异常场响应如图14所示,y=500 m异常场场值变化曲线如图15所示.综合图14和图15,1从0.01 SI变化至100 SI,ΔT、Bax、Bay、Baz四个分量场幅值增大,但形态变化较小.其中1改变对Bay场值形态轮廓的变化几乎无影响.类比可知,当HTI-Y介质主轴磁化率2变化,Bax形态也基本不变.

图14 HTI-X介质不同1 磁异常场响应(z=0 m平面)
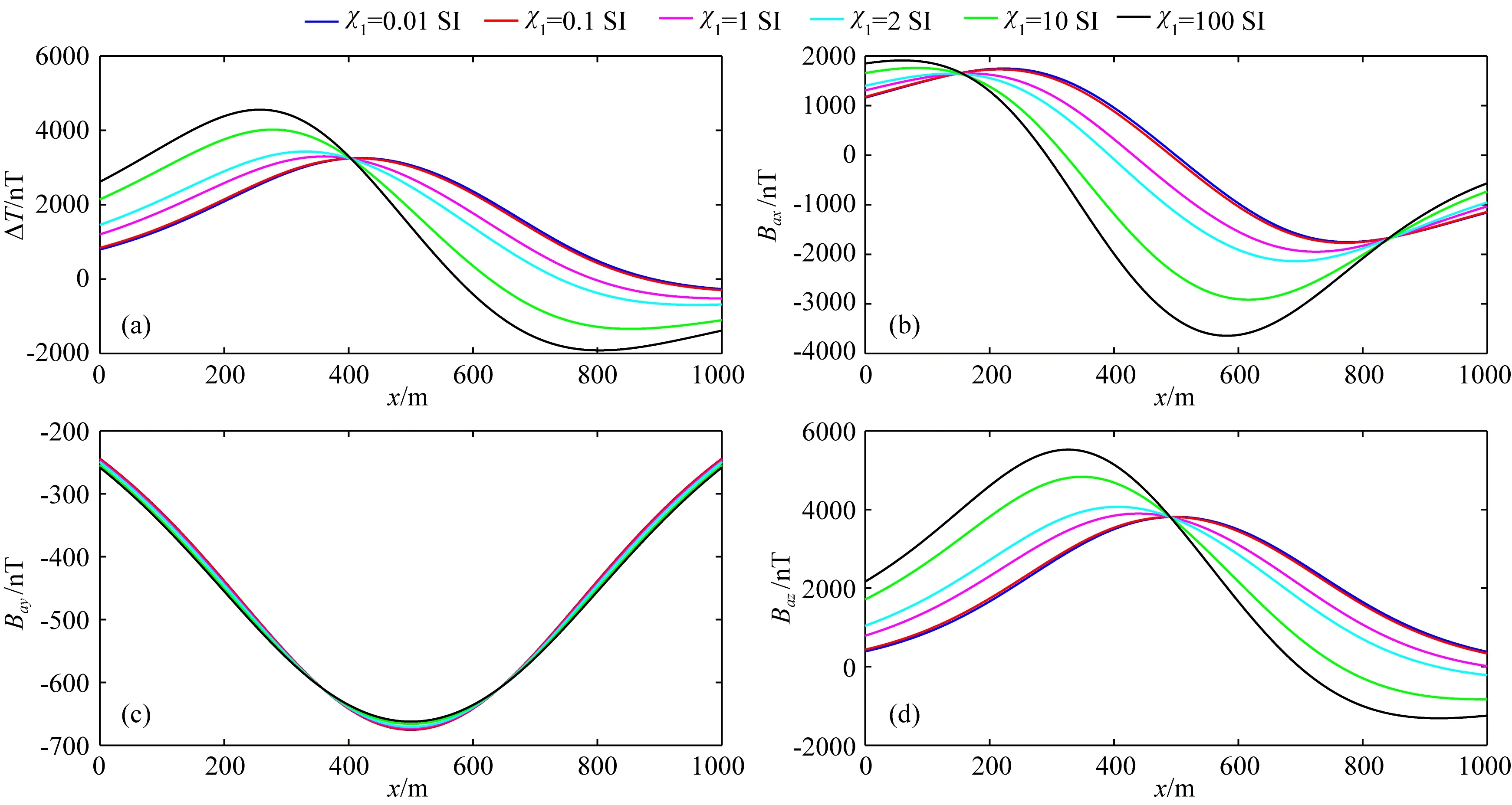
图15 HTI-X介质不同1磁异常场曲线(y=500 m)
5.3 TTI介质
将VTI介质或HTI介质进行坐标旋转,即可变为TTI介质.本小节选择将VTI介质进行旋转,磁化率主轴1=2=2 SI,3=0.1 SI,欧拉角β=γ=0°,将介质在yoz平面内绕x轴旋转,即改变欧拉角α.将α分别设为0°、30°、45°、60°、90°.易知,当α为0°时,介质为VTI介质,α为90°时,介质为HTI-Y介质.不同欧拉角α介质各向异性特征变化过程如图16所示.

图16 不同欧拉角α各向异性介质特征
z=0 m平面VTI介质随欧拉角α从0°变化至90°时磁异常场响应如图17所示,y=500 m异常场场值曲线变化如图18所示.综合图17和图18,在本节设计的模型参数下,α从0°逐渐增大至90°,ΔT、Bax、Bay、Baz四个分量场值形态均发生较大改变,其幅值也逐渐增大,α为90°时达到最大,此时1和3互换数值,1>3,因此异常场幅值变大.
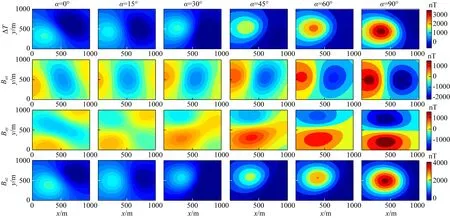
图17 TTI介质不同欧拉角α磁异常场响应(z=0 m平面)
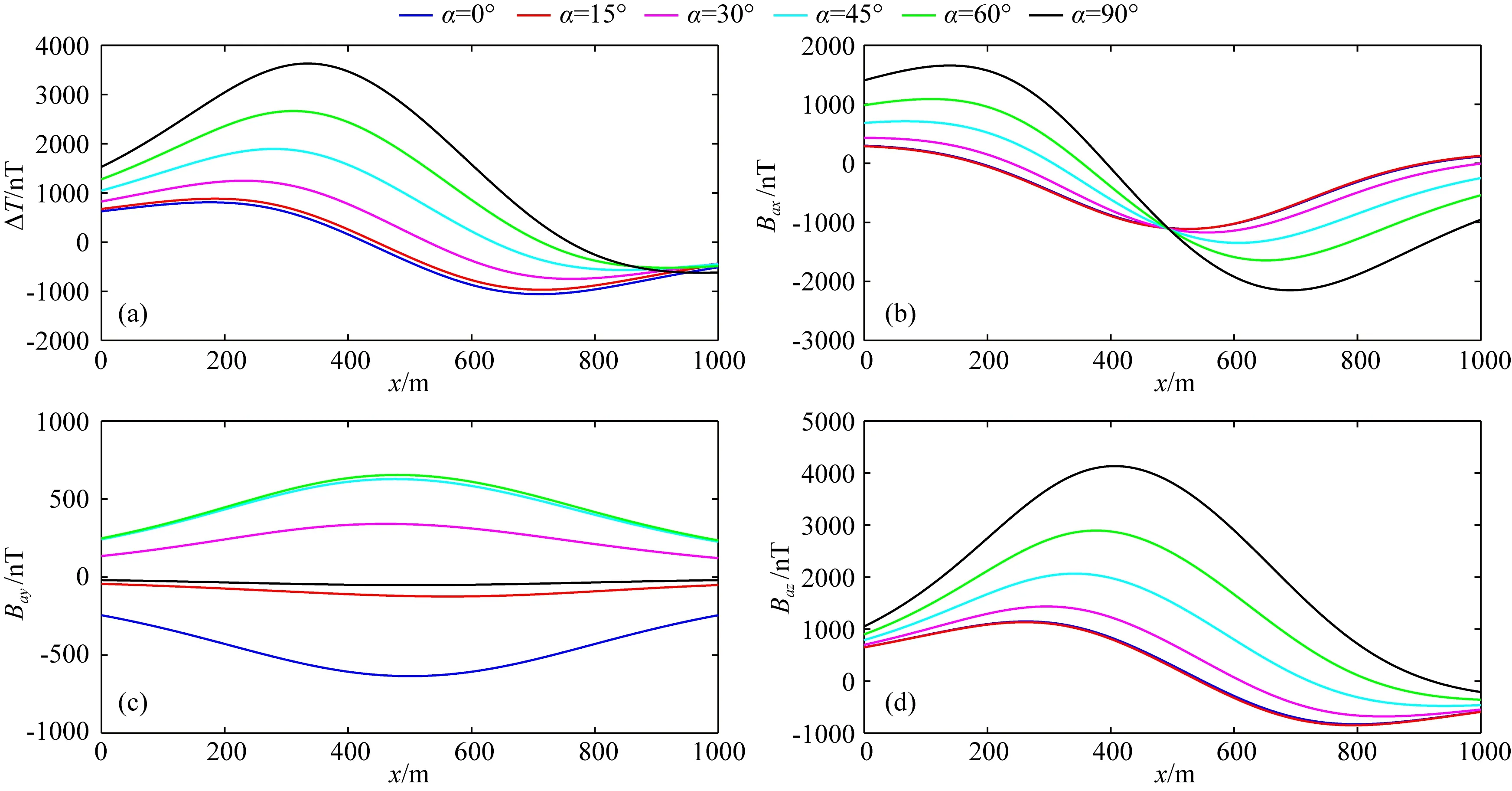
图18 TTI介质不同欧拉角α磁异常场曲线(y=500 m)
综合上述VTI介质、HTI介质和TTI介质不同各向异性参数的磁场响应特征分析,当欧拉角均为0时,仅改变1对Bay形态变化几乎无影响;仅改变2对Bax形态变化几乎无影响;仅改变3对ΔT、Bax、Bay、Baz四个分量的幅值和形态均有影响.当欧拉角不为0时,对ΔT、Bax、Bay、Baz四个分量的幅值和形态均有影响.
6 起伏地形条件下各向异性强磁场响应
研究起伏地形条件下各向异性强磁性体磁场响应,设计多个强磁性体组合模型,并加入实际起伏地形数据进行数值模拟.
一般情况下,为计算起伏地形面上磁场分布,在起伏地形最高点与最低点之间设置多个不同深度的水平面,计算这些水平面的磁场,最后通过插值得到起伏地形面上磁异常场分布.
从国家地理空间数据云获得某磁铁矿起伏地形数据,取西南角顶点为坐标原点,忽略大地水准面曲率,其DEM高程如图19所示.南北和东西方向延伸均为10 km,地形最大高程差260 m.当地背景磁场强度487534 nT,磁倾角41.7°,磁偏角-1.6°.模型计算范围x、y方向都为[0 m,10000 m],z方向[-260 m,1000 m],地形最低点在z=0 m平面,地形最高点在z=-260 m平面.剖分节点个数为201×201×253,其中起伏地形所占垂直方向节点个数为53.在起伏地形最低点以下设计椭球体、球体、长方体等四个异常体,分别代表条带状、球形、板状铁磁性异常,异常体参数如表4所示.实际起伏地形与异常体位置关系三维可视化示意图如图20所示.
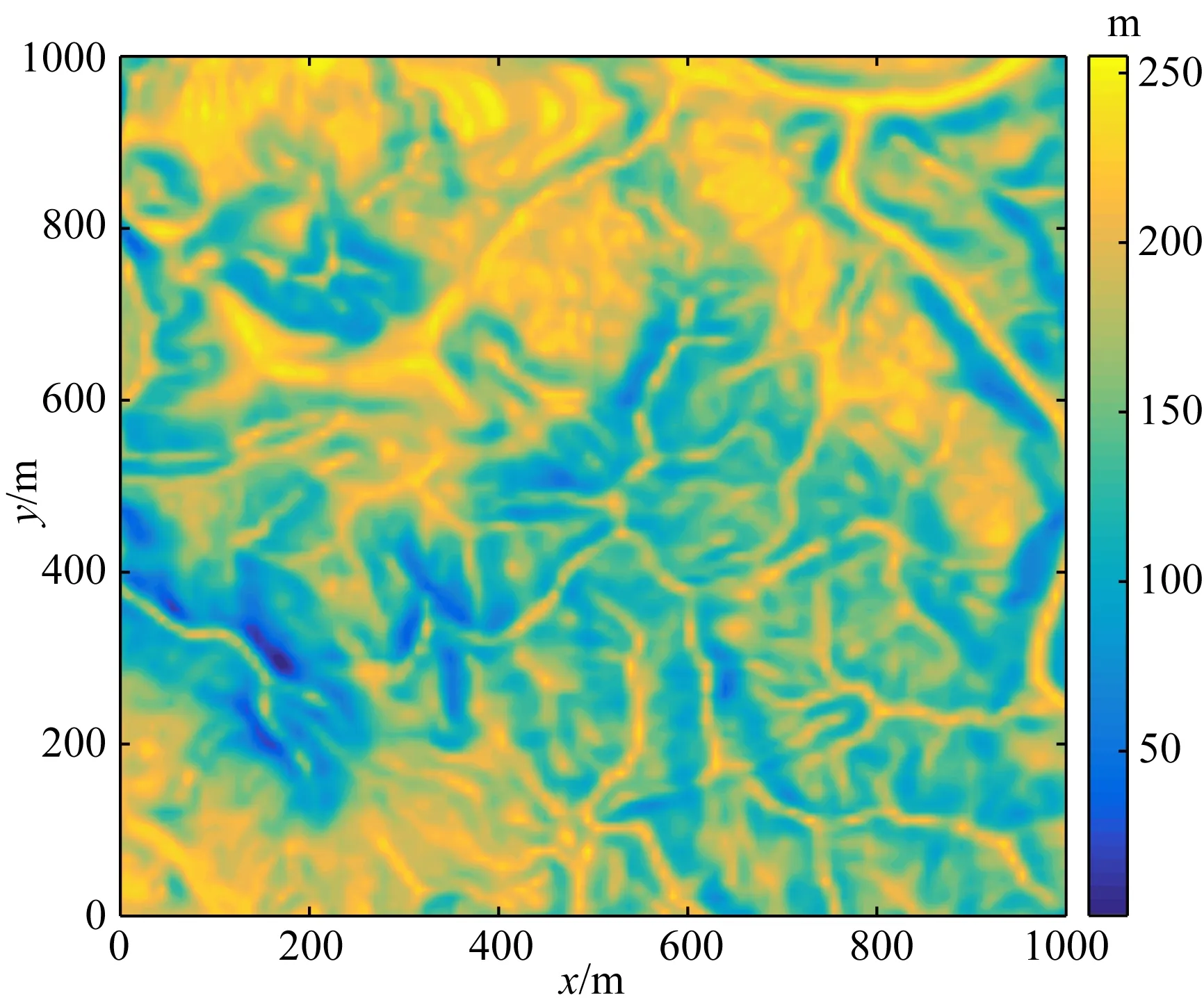
图19 DEM高程数据
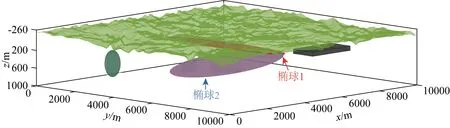
图20 DEM高程数据与复杂模型空间位置示意图

表4 异常体参数
利用起伏地形上53个平面上的节点计算起伏地形面上磁异常场,并与z=-260 m平面磁异常场进行对比,结果如图21所示,其中第1列为z=-260 m平面异常场,第2列为起伏地形面上异常场,第3列为y=5000 m 时x方向异常场对比曲线.从图21可知,两个面上的磁异常场形态和幅值存在差异,平面上的磁异常场对地下异常体形态和轮廓识别效果更好;相对于z=-260 m平面异常场,在地形起伏面上,地形海拔低处场值增强,异常场形态发生改变,对异常体边界识别能力减弱;起伏面上异常场等值线变化是磁化率异常体模型和起伏地形变化的综合体现,表明本文算法对复杂地形的适应性.
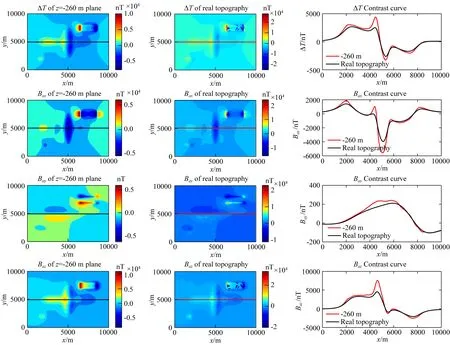
图21 z=-260 m平面及起伏地形面上异常场和对比曲线
7 结论
本文提出一种针对各向异性强磁性体磁场数值模拟的空间-波数混合域方法,该方法对各向异性强磁体磁位满足的三维偏微分方程进行二维傅里叶变换,将三维空间方程转变为不同波数满足的一维偏微分方程,引入紧算子迭代求解,实现各向异性强磁介质磁场高效、高精度数值模拟.取得如下结论:
(1)与各向异性椭球体模型的解析解对比,验证了本文算法的正确性.
(2)各向异性强磁性体磁化率张量各参数对算法的迭代收敛性有影响,且磁化率主轴分量越大,算法迭代次数越多,但都稳定收敛.
(3)与COMSOL软件对比计算效率,在相同网格剖分条件下,表明本文算法计算效率更高,且计算节点总数越多,优势越明显.
(4)分析了VTI、HTI和 TTI介质中各向异性磁化率张量参数的变化对磁异常场响应特征的影响,表明磁化率主轴和欧拉角改变会影响场的幅值和形态,强磁性体各向异性特征对磁场的影响不可忽略.
(5)利用DEM高程数据建立带地形的各向异性磁化率模型,相对平面上磁异常场,起伏地形面上场值形态和数值发生变化,表明算法适用于起伏地形条件下任意复杂模型的数值模拟.
附录A
针对边值问题(式(16)),构造泛函:
(A1)
式中:
(A2)
式(A1)变分为:
(A3)
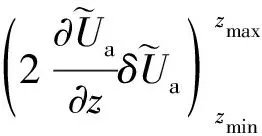
(A4)
将边界条件式(14)、(15)代入式(A4),可得:
(A5)
因此:
(A6)
因此空间波数域异常磁位边值问题与变分问题等价:
(A7)
附录B
将整个区域单元积分分解成各个单元积分之和,则式(A7)可写为:
(B1)
令:
(B2)
则:
(B3)
式(B1)中第一项单元积分为:
(B4)
式中:
(B5)
式(B1)中第二项单元积分为:
(B6)
式中:
(B7)
式(B1)中第三项单元积分为:
(B8)
(B9)
式中:
(B10)
所以式(B8)中第一项单元积分为:

(B11)
式中:
(B12)
式(B8)中第二项单元积分为:
(B13)
式中:
(B14)
式(B8)中第三项单元积分为:
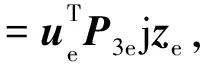
(B15)
式中:
(B16)
式(B1)中zmin、zmax分别为垂直方向第一个和最后一个节点,可将其扩展为:
(B17)
式中:
(B18)
综上,可将式(B1)表示为:
(B19)
