地铁列车振动规律实测与分析

孟禹，任青，唐家进

（上海理工大学 环境建筑学院，上海 20093）

随着科技的迅速发展及经济水平的显著提高，国内城市化的步伐越迈越快，然而人口相对集中，导致城市交通系统承受的压力越来越大。因此，地铁交通凭借着运行速度快、载客量大、舒适性强、安全性高、运行时间固定可靠、对环境污染极小等优点已成为城市交通工具的首选，具有良好的社会效益[1-2]。然而，人们在享受发达交通方式带来便利的同时，高速列车、地铁、城市道路交通等引起的振动对环境的影响也愈发突出[3]。目前，交通引起的振动已被列为七大环境公害之一，为此国内外相关领域的科研从业者多年来一直致力于研究交通所引起振动的传播途径、振动规律、控制方法等。本文选择了上海地铁2 号线苏虹路和闵行高架线交叉口附近为测试场地。根据实测数据分析了轨道交通引起环境振动的衰减特性。

1 振动测试

1.1 测试地点

综合考虑地铁运营时间及各测试场地的实际情况，上海地铁2 号线和上海地铁13 号线的测点布置如下：

上海地铁2 号线。测试地点定在苏虹路和闵行高架线交叉处附近，在距离地铁中心线处设置了监测点共11个，如图1 所示。苏虹路和闵行高架线到最近测点的距离大于200m，地面交通振动对测试的干扰较小。

图1 上海地铁2 号线测试点位图

1.2 测试设备

拾振器。本文现场测试使用的是低频高解析度加速度传感器(PCB-393B05)，

采集与分析系统。本文现场实测使用课题组自行研发的便携式微振动量测系统，本文选取地面环境振动有效数据并使用 BDSA 软件对数据进行处理分析，分析内容包括频谱分析及 1/3 倍频程分析[4]。以200Hz 采样频率测取各测试点位的Z 向、EW 向和NS 向地铁振源激励下的振动信号，部分测试区域地面主要覆盖泥土，故在测量时用铁椎打入土体中，再将拾振器放在铁锥顶部平台上，在顶部平台调节至水平后放置拾振器。测试时间选择在夜间22：00 以后，测试人员严禁随意走动。

1.3 测试结果分析

1.3.1 上海地铁2 号线

1.3.1.1 Z 向频谱曲线分析

取距离地铁最近处的测点（0m）和加速度峰值衰减开始的平缓的测点（60m）的频谱曲线进行比较，用于研究地铁振动频率成分的改变情况[5]。

由图2 可知，该测试场地的自振频率在4Hz 左右；最优频率在72Hz 左右，测点60m 处Z 向振动分布在10～20Hz 和90～100Hz，最优频率在16Hz 左右，可以看出，随着到地铁中心线距离的增加，Z 向最优频率有所减小，对应的幅值有所减小。

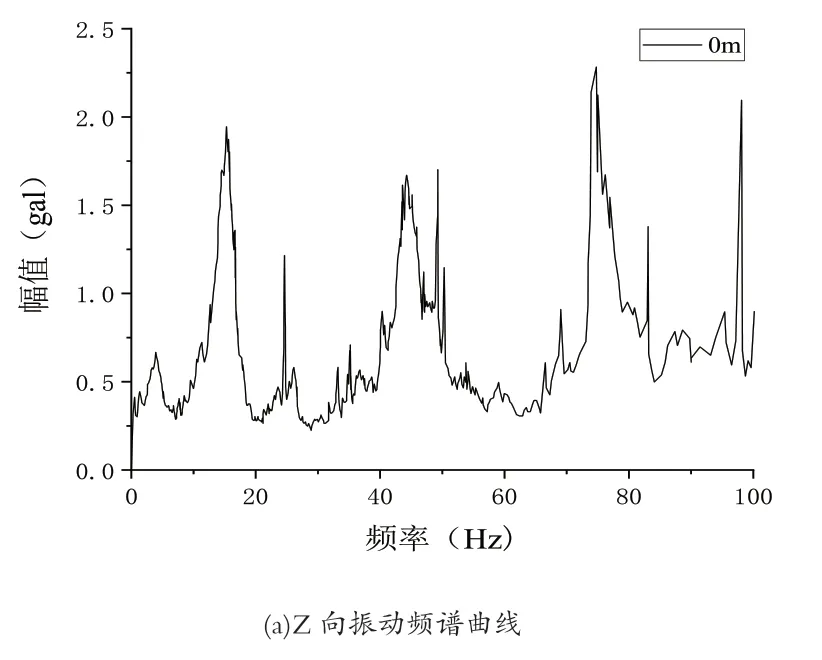
图2 不同测点Z 向的环境振动频谱曲线

1.3.1.2 1/3 倍频程分析

由图3（a）～（f）可知，该测试地点地铁运行诱发地面振动的Z 向、EW 向、NS 向振动能量均集中在16～80Hz 中心频率范围内。

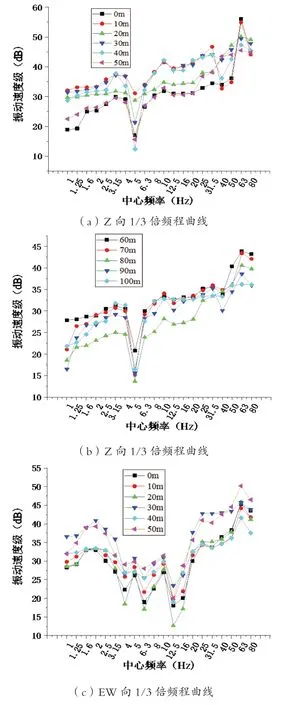
图3 各测点1/3 倍频程曲线

Z 向振动速度级在1～4Hz 和10～31.5Hz 中心频率范围内随频率的增加变化较为平稳；在4～5 Hz 和31.5～40 Hz 中心频率范围内振动速度级随着频率的增加而波动减小且在4～5Hz 中心频率范围内衰退速率更显著；在5～8 Hz 和 40～80 Hz 中心频率范围内振动速度级随着频率的增加而波动增加，且在5～8 Hz 中心频率范围内尤为迅速。

EW 向振动速度级在1～2 Hz 和12.5～80 Hz 中心频率范围内随着频率的增加而波动增加，且 12.5～25 Hz 增加速率最快；在2～12.5 Hz 中心频率范围内随着频率的增加呈“锯齿”型减小，在10～12.5 Hz 中心频率范围内随着频率的增加减小的最为剧烈。

NS 向振动速度级在1～80Hz 中心频率范围内整体呈现随频率增加而上升趋势，但在不同频率范围增加的趋势不尽相同，在1～4Hz 中心频率范围内随着频率的增加而显著增加，在4～25 Hz 中心频率范围内随着频率的增加而平稳缓慢增加、25～80Hz 中心频率范围内随着频率的增加而升降走势较为反复。

2 结果与讨论

本文通过对上海地铁2 号线进行了大量的现场实测并分析采集的数据，得出了如下结论：

（1）地铁运行诱发环境振动的振动响应Z 向大于水平向；无论是竖直向（Z 向）还是水平向（EW 向和NS 向），均随着距离地铁中心线距离越来越远，振动响应越来越小；地铁运行引起地面振动加速度在近处衰减幅度大且衰减速率快，在远处衰减幅度小且衰减速率慢；地铁运行引起地面振动在距离地铁中心线30m 左右处存在振动放大区；地铁运行引起地面振动的振动能量集中在20～80Hz 中心频率范围内；随着测点到地铁中心线距离的推远，振动速度级幅值对应的中心频率范围有所缩小。地铁列车的振动影响范围约为距离轨道中心线500m。

（2）地铁埋深越大引起的地面Z 向振动响应越小且衰退得越快，地铁埋深相差在5m 以内时对水平方向的振动响应无明显影响。地铁运行时地面的振动速度级与到地铁中心线距离之间基本呈现对数关系。