基于循环冲击加速试验的某O型橡胶密封圈寿命评估方法

王艳艳，秦朝轩，赵方超，朱浩若

武器装备

基于循环冲击加速试验的某O型橡胶密封圈寿命评估方法

王艳艳，秦朝轩，赵方超，朱浩若

（西南技术工程研究所，重庆 400039）

快速准确评估温度循环条件下某O型橡胶密封圈的贮存寿命。模拟O型橡胶密封圈真实受压状况，设计专用夹具，在4个应力条件下开展温度循环冲击加速寿命试验，获得密封圈退化数据，分析并获得密封圈伪失效寿命，构建修正Coffin-Manson模型，并利用不同试验条件下得到的伪失效寿命数据对模型进行参数估计，获得Coffin-Manson寿命预估模型，外推常温条件下密封圈的贮存寿命。通过试验表明，指数模型相比对数模型与线性模型能更准确描述密封圈的退化情况，经Coffin-Manson模型评估，该O型橡胶密封圈常温条件下的贮存寿命为6.13 a，与工程经验数据吻合。所提出的基于循环冲击加速试验的O型橡胶密封圈寿命评估方法可以准确评估密封圈的贮存寿命，大大缩短试验周期，节省寿命评估试验时间和成本，为密封器件的寿命评估提供了参考。

密封圈；寿命评估；温度循环；加速寿命试验；Coffin-Manson模型；夹具

橡胶密封圈是一种常用的密封器件，由于其高分子材料的固有特点，在加工、贮存和使用过程中会发生老化现象，最终导致密封失效。对于具有“长期贮存，一次使用”的弹药产品而言，橡胶密封圈是一个典型的薄弱环节，其贮存寿命直接影响着整弹的可靠性。因此，对橡胶圈进行准确的寿命预测对于弹药产品的定寿评寿、关键部件的维修和更换具有极高的参考价值。

常用的寿命评估手段包括自然贮存试验以及加速寿命试验，自然贮存试验的结果真实可靠，然而由于产品许多设计寿命较长，因此自然贮存试验难以快速获得产品寿命信息；而加速寿命试验通过提高试验应力，加速产品失效过程，大大缩短了试验周期，因此受到学者广泛关注。张晓军等[1]对氟橡胶密封材料进行了热氧加速老化试验，外推氟橡胶密封件常温下的贮存寿命为13.8 a。张鑫等[2]研究了航空电子装备的加速寿命试验方法。Kim等[3]将电流作为加速应力，提出了基于逆幂律的励磁涌流电寿命模型，并对继电器进行了寿命评估。周小燕等[4]研究了激光探测器贮存寿命的影响因素，并设计了加速寿命试验对其进行评估。Kim等[5]选取电压、振动和温度作为加速变量，利用威布尔寿命分布和寿命–应力关系的广义线性模型，对白炽灯进行了寿命评估。目前最为常用的寿命评估方法是通过加速寿命试验结合阿伦尼乌斯模型来评估产品在常温下的贮存寿命[6-10]，Dixon[11]利用阿伦尼乌斯模型外推法推算了其他温度下材料的老化状况。张凯等[12]利用阿伦尼乌斯模型对旧橡胶密封圈进行了贮存寿命评估。该方法在恒温条件下可以取得不错的效果，然而阿伦尼乌斯方程假定活化能与温度无关，忽略了温度对活化能的影响，造成了评估结果的偏差，然而实际产品贮存过程中常常伴随着白天–晚上以及夏季–冬季的温度交替变化。因此，有学者提出了温度循环加速试验[13]。温度循环试验可用于考核产品对周围环境温度急剧变化的适应性，是弹箭产品设计定型的鉴定试验和批生产阶段的例行试验中不可缺少的试验项目，温度循环试验在验证和提高弹箭产品的环境适应性方面应用的频度仅次于振动与高低温试验。对于温度循环加速试验，学者常用Coffin-Manson进行寿命评估[14-17]。赵帅帅等[18]针对温度循环应力下加速寿命试验数据处理困难而限制其应用的问题，采用了一种基于修正Coffin-Manson模型的加速寿命试验设计与评估方法，运用Monte Carlo仿真实例进行分析验证。陈克凡等[19]利用修正Coffin-Manson模型建立了混凝土温度循环加速因子模型，并对橡胶混凝土进行了可靠寿命预估。

本文以某弹用O型橡胶密封圈为研究对象，设计温度循环加速寿命试验，引入修正Coffin-Manson模型作为加速模型，对橡胶圈可靠寿命进行评估，技术路线如图1所示。首先模拟橡胶密封圈真实受压情况，设计工装夹具，进而设计温度循环冲击试验谱，开展加速寿命试验。获得加速寿命条件下的退化数据后，构建适用模型，计算伪失效寿命，进而构建修正的Coffin-Manson模型，利用多元回归求解参数，外推常温贮存寿命。

图1 O型橡胶密封圈寿命评估技术路线

1 试验方案设计

1.1 试验样本及失效判定

试验样品为某O型橡胶密封圈，其材料为丁腈混炼橡胶试5171，满足GJB 250A—1996《耐液压油和燃油丁腈橡胶胶料规范》要求。样品数量为20件。径向截面原始尺寸约为2.5 mm。按验收技术条件的规定，以压缩永久变形率达到50%作为临界指标。

1.2 试验工装设计

由于密封圈在弹中为受压状态，设计方以及使用方更为关注的是密封圈随弹贮存的寿命，因此需要真实模拟密封圈在产品中的真实受压状况。为达到该效果，设计工装夹具如图2所示，压缩后的高度（夹具限制器高度）为1.85 mm。

图2 橡胶O型密封圈工装夹具安装示意图

1.3 温度循环加速试验

研究表明，橡胶密封圈在贮存过程中，引起其老化的环境因素主要是温度[20]。温度循环加速了热胀冷缩效应，使产品交替膨胀和收缩，在样品中产生了应力的循环。若产品内有热梯度，则热应力会加剧，潜在缺陷会随循环数的增加而被激发，易造成结构性破坏。同时，温度循环试验模拟自然贮存状态下的高低温变化。温度冲击和高/低温浸透，会造成复合材料分层、表面防护涂层剥离、密封橡胶老化等现象，产品的密封、防护被破坏，贮存环境空气中的水分子及其他腐蚀性气体进入产品内部，导致产品性能发生退化、改变，进而发生故障。该方法较常规的加速试验具有加速效率高、试验时间短的特点，适合于对温湿度变化贮存损伤敏感的弹药部器件类，包括导引头、控制舱橡胶密封件等。

温度循环加速寿命试验剖面要素有：温变范围、温变率、最高温度、温度保持时间。加速应力下环境剖面需要在贮存环境剖面的基础上进行加严，并要求保证失效机理不发生改变。加速的因素主要考虑温变范围、温变率和最高温度，温度保持时间则主要保证产品热透、冷透，产品内部温度与环境温度相差在允许范围内。

温度保持时间以保透为准。对体积较大的被试品，参考国军标，最低温度为–55 ℃，保持36～48 h；最高温度为70 ℃，保持时间为24～36 h；对于体积较小的被试品，低温保持4～6 h，高温保持4～6 h。每一个循环周期为4 h：升温时间为17 min，高温保持时间146 min，降温时间为17 min，低温保持时间为1 h，温度控制偏差为±2 ℃，本文的温度循环冲击加速寿命试验剖面如图3所示。设置4个试验条件，详细信息见表1，每个试验条件下放置5个样本。每2 d对样本进行1次检测，检测其压缩回弹高度。

图3 橡胶密封圈温度循环冲击加速寿命试验剖面

表1 橡胶密封圈温度循环冲击试验应力条件

Tab.1 Stress conditions of temperature cycling impact test for rubber seal ring

2 寿命评估模型建立

计算样品的压缩永久变形率[21-23]作为其性能退化失效判定依据：

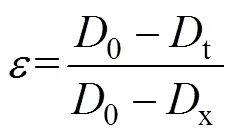
式中：为密封圈的压缩永久变形率；0为密封圈样品的原始轴向厚度值；t为在加速试验过程中检测得到的样品轴向厚度值；x为夹具限制高度。

橡胶密封圈的失效行为通常表现为退化失效，常见的退化模型包括指数模型[24]、对数模型以及线性模型，分别见式（2）—（4）。

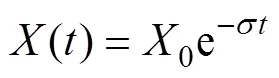
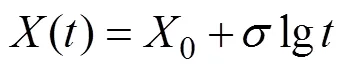
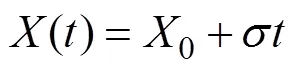
式中：0为样本初始性能参数；()为样本退化至时刻时的性能参数；为时间；为模型参数。

利用相关系数作为模型的拟合程度[25]检验：

橡胶密封圈在温度循环试验下采用修正的Coffin-Manson模型[26-27]：

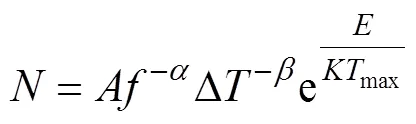
式中：为在该温度循环条件下到达失效阈值的失效循环次数，与寿命密切相关；为循环频率，即单位时间内温度循环的次数，cycle/h；Δ为温度差，即温度最高值与最低值之间的差值，K，max为循环温度的最大值，K；为玻尔兹曼常数，=8.617×10–5eV/K；为激活能；、、为模型参数。

为方便计算，对式（6）两边取对数得到：

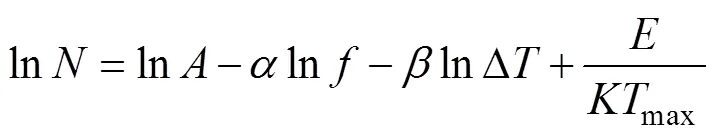
由修正的Coffin-Manson模型适可导出加速因子为：

其中：L、H分别为低、高应力下的失效循环数；ΔL、ΔH别为低、高应力下的温度变化幅度；L、H分别为低、高应力下的循环频率；mL、mH分别为低、高应力循环中的最高温度。

其对数形式为：

当L=H时，不同应力水平保持循环频率不变，此时加速因子为：

当ΔL=ΔH，且mL=mH时，不同应力水平下保持温度变化范围和最高温不变，此时加速因子为：

当ΔL=ΔH，且L=H时，不同应力水平下保持温度变化范围和循环频率不变，此时加速因子为：

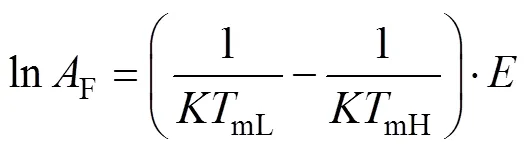
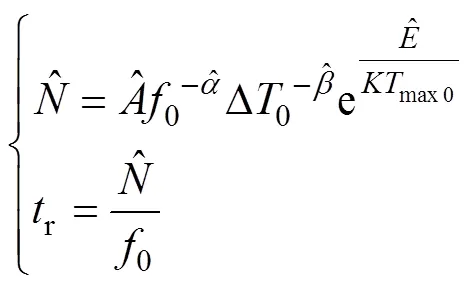
3 试验结果及分析

本文设置了4个试验应力水平，每个应力水平下有5个试验样本，总试验时间为30 d，每间隔1 d对样品进行1次压缩回弹高度的测试，对每个样本进行5个点的测试，计算测试结果的平均值作为其性能参数值，得到的加速性能退化试验数据见图4和表2。从图4中可以看出，随着加速寿命试验的进行，样本的压缩回弹高度均发生了一定的退化。通过计算样本的压缩永久变形率可以发现，在30 d内的加速老化过程中，样本没有发生失效，因此可以利用检测到的退化数据计算其伪失效寿命。

对橡胶密封圈加速寿命试验的性能数据分别采用线性退化模型、指数退化模型和对数退化模型进行回归分析，分析结果见表3。可以看出，指数模型所计算出的相关系数最高，表明该橡胶密封圈的性能退化服从指数分布，因此可以利用指数模型计算样本在不同试验条件下的伪失效寿命。结合产品的失效判定依据，根据式（2）计算样本的伪失效寿命，计算结果见表4。

表2 橡胶密封圈不同试验条件下压缩永久变形率均值

Tab.2 Average compression springback height of rubber seal ring under different test conditions %

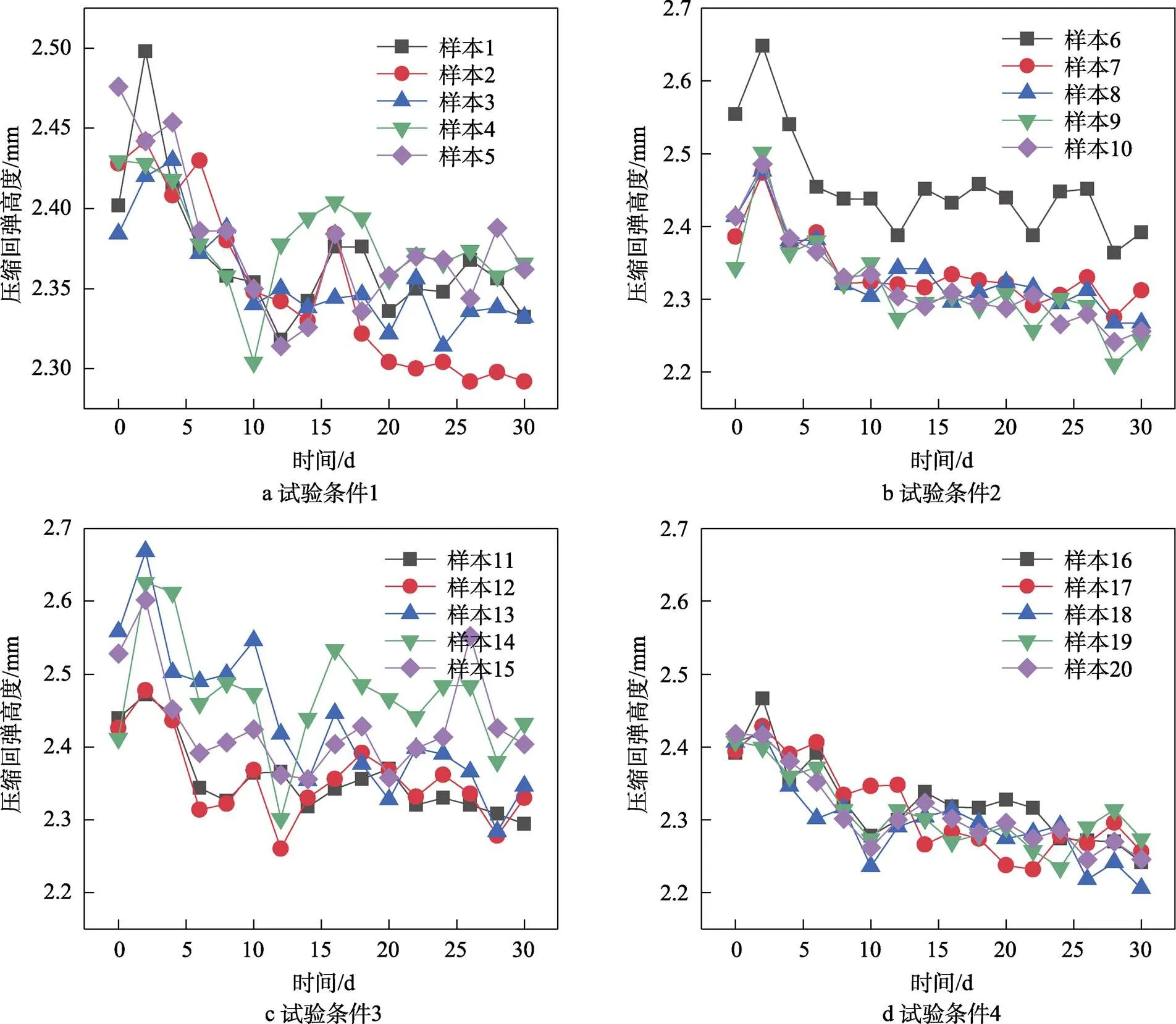
图4 不同试验条件下密封圈样品的性能退化曲线

表3 不同退化模型的相关系数计算结果

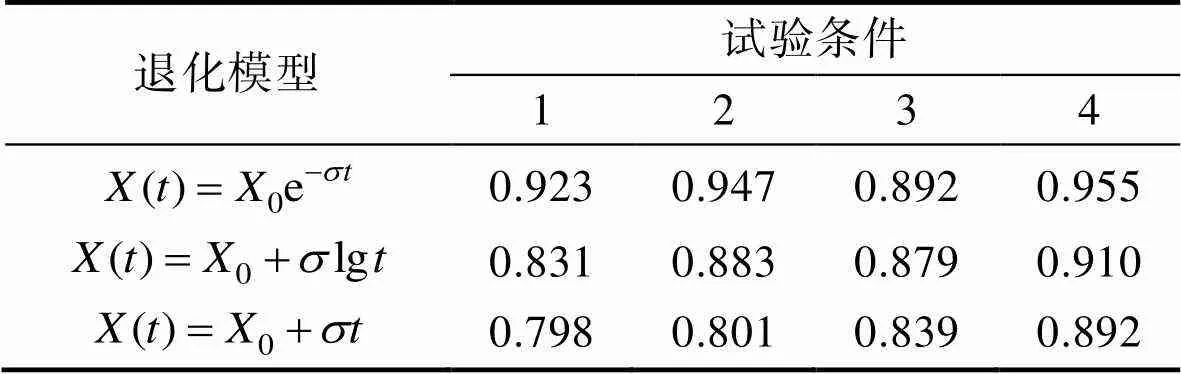
Tab.3 Calculation results of correlation coefficients of different degradation models

表4 不同试验条件下的性能退化模型和伪失效寿命

Tab.4 Performance degradation model and false failure life under different test conditions

根据表4获得的伪失效寿命数据，利用多元回归分析对Coffin-Manson模型的参数进行估计，将参数估计结果代入模型中得到：

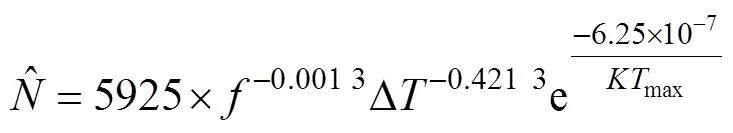
因此，将常温贮存条件的相关参数代入式（14）中，计算得到正常应力条件下的贮存寿命为6.13 a，结果见表5。

表5 正常应力水平下密封圈的贮存寿命

Tab.5 Storage life of seal ring at normal stress level

根据该产品的设计寿命以及实际贮存经验，在常温贮存条件下，该O型橡胶密封圈的贮存寿命约为6.3 a，与本文所计算出的结果非常吻合，在工程上可以接受，表明本文提出的基于循环冲击加速试验的寿命评估方法是合理有效的。

对该样品开展恒定应力加速寿命试验，与温度循环加速寿命试验结果进行对比，选取323.15 K（50 ℃）与343.15 K（70 ℃）温度应力，定期对样品进行检测，得到样品的压缩永久变形率，结果见表6。与表2的结果进行对比可以发现，在323.15 K温度应力下，样品加速退化30 d时，恒定应力加速寿命试验的压缩永久变形率退化量为17%，而温度循环加速寿命试验的退化量为20.62（15 min温变速率）和25.85（5 min温变速率）；在343.15 K温度条件下，恒定应力加速寿命试验的压缩永久变形率退化量为22%，温度循环加速寿命试验的退化量为32%（5 min温变速率）和25.85%（15 min温变速率），温度循环加速寿命试验样品的退化量大于恒定应力加速寿命试验。因此，验证了温度循环加速寿命试验缩短了加速寿命试验的周期，提高了试验效率，相比于恒定温度加速寿命试验，可以更快地获得样品薄弱环节信息。

表6 恒定应力加速寿命试验的压缩永久变形率

Tab.6 Compression set rate results of acceleration life test at constant stress %

4 结论

为有效评估某O型橡胶密封圈贮存寿命，本文提出一种基于循环冲击加速试验的寿命评估方法。为模拟密封圈真实受压状况，设计了试验专用夹具。在4个温度循环加速试验条件下开展试验，获得了密封圈样本退化失效数据，通过相关系数验证了密封圈退化过程符合指数分布模型。结合产品设计失效阈值，估算了不同试验条件下产品的伪失效寿命。采用最小二乘算法对Coffin-Manson模型进行参数估计，外推出常温贮存条件下该O型橡胶密封圈的贮存寿命为6.13 a。该结果与工程经验数据吻合，表明本文所提出的方法可以快速有效地评估O型橡胶密封圈贮存寿命，节省了寿命评估试验时间和成本，为密封器件的寿命评估提供了参考。

[1] 张晓军, 常新龙, 陈顺祥, 等. 氟橡胶密封材料热氧老化试验与寿命评估[J]. 装备环境工程, 2012, 9(4): 35-38.

ZHANG Xiao-jun, CHANG Xin-long, CHEN Shun- xiang, et al. Thermal Oxidation Aging Test and Life As­sessment of Fluorine Rubber Sealing Materials[J]. Equip­ment Environmental Engineering, 2012, 9(4): 35-38.

[2] 张鑫, 韩建立, 张信明, 等. 航空电子设备加速可靠性试验有限元分析应用进展[J]. 装备环境工程, 2021, 18(9): 27-34.

ZHANG Xin, HAN Jian-li, ZHANG Xin-ming, et al. Progress in Finite Element Analysis of Accelerated Reliability Test for Avionics[J]. Equipment Environmental Engineering, 2021, 18(9): 27-34.

[3] KIM J J, CHANG S W, SON Y K. Electrical Lifetime Estimation of a Relay by Accelerated Life Test[J]. Transactions of the Korean Society of Mechanical Engineers A, 2008, 32(5): 430-436.

[4] 周小燕, 梁晨宇, 姜超, 等. 弹载激光探测器加速寿命试验与评估研究[J]. 激光与红外, 2021, 51(5): 629-633.

ZHOU Xiao-yan, LIANG Chen-yu, JIANG Chao, et al. Study on Accelerated Life Test and Evaluation of Missile Borne Laser Detectors[J]. Laser & Infrared, 2021, 51(5): 629-633.

[5] KIM J W, SHIN J C, KIM M S, et al. An Accelerated Life Test for Burnout of Tungsten Filament of Incandescent Lamp[J]. Transactions of the Korean Society of Mechanical Engineers A, 2005, 29(7): 921-929.

[6] 周堃, 胡滨, 王津梅, 等. 阿伦尼乌斯公式在弹箭贮存寿命评估中的应用[J]. 装备环境工程, 2011, 8(4): 1-4.

ZHOU Kun, HU Bin, WANG Jin-mei, et al. Application of Arrhenius Equation in Storage Life Evaluation of Ammunition[J]. Equipment Environmental Engineering, 2011, 8(4): 1-4.

[7] ZHAO Xin, RUI Xiao-ting, WANG Yan, et al. A Novel Method for Prediction of Propellant Shelf-Life Based on Arrhenius Equation[J]. Propellants, Explosives, Pyrotechnics, 2018, 43(4): 348-354.

[8] 柯玉超, 王识君, 吴蕾. 基于加速老化的橡胶密封件使用寿命评估[J]. 液压气动与密封, 2018, 38(12): 79-83.

KE Yu-chao, WANG Shi-jun, WU Lei. The Lifespan Prediction of Rubbers through Temperature Accelerated Aging[J]. Hydraulics Pneumatics & Seals, 2018, 38(12): 79-83.

[9] 周鑫, 丁孝均, 魏威. 加速老化试验方法评估典型橡胶密封材料贮存寿命的准确性研究[J]. 航天器环境工程, 2014, 31(3): 287-291.

ZHOU Xin, DING Xiao-jun, WEI Wei. Accuracy on Evaluation of Natural Storage Life of Rubbery Sealing Materials by Using Accelerated Life Method[J]. Spacecraft Environment Engineering, 2014, 31(3): 287-291.

[10] 董建新. 基于老化的水润滑橡胶尾轴承可靠性寿命评估[D]. 武汉: 武汉理工大学, 2013.

DONG Jian-xin. Assessing the Reliability Life of Water Lubrication Stern Tube Rubber Bearings with Aging[D]. Wuhan: Wuhan University of Technology, 2013.

[11] DIXON R R. Thermal Aging Predictions from an Arrhenus Plot with only one Data Point[J]. IEEE Transactions on Electrical Insulation, 1980, 15(4): 331-334.

[12] 张凯, 周堃, 何建新. 一种橡胶密封圈的剩余贮存寿命评估方法[J]. 装备环境工程, 2018, 15(4): 95-97.

ZHANG Kai, ZHOU Kun, HE Jian-xin. Assessment Method for Residual Storage Life of Rubber Sealing Ring[J]. Equipment Environmental Engineering, 2018, 15(4): 95-97.

[13] SHIH T I, LIN Y C, DUH J G, et al. Electrical Characteristics for Sn-Ag-Cu Solder Bump with Ti/Ni/Cu Under-Bump Metallization after Temperature Cycling Tests[J]. Journal of Electronic Materials, 2006, 35(10): 1773-1780.

[14] 赖伟. 计及低强度热载荷疲劳累积效应的IGBT功率器件寿命模型研究[D]. 重庆: 重庆大学, 2016.

LAI Wei. Study on Lifetime Modeling of IGBT Module Considering Fatigue Accumulative Effect of Narrow Junction Temperature Cycles[D]. Chongqing: Chongqing University, 2016.

[15] 吕红杰, 江国栋, 汪张超. 基于Coffin-Manson模型评价一种过渡件焊接结构的可靠性[J]. 电子质量, 2019(9): 24-29.

LV Hong-jie, JIANG Guo-dong, WANG Zhang-chao. Evaluation on the Reliability of a Kind of Transition Welding Structure Based on Coffin-Manson Model[J]. Electronics Quality, 2019(9): 24-29.

[16] RUNCIMAN A, XU D, PELTON A R, et al. An Equivalent Strain/Coffin-Manson Approach to Multiaxial Fatigue and Life Prediction in Superelastic Nitinol Medical Devices[J]. Biomaterials, 2011, 32(22): 4987-4993.

[17] SHOHJI I, MORI H, ORII Y. Solder Joint Reliability Evaluation of Chip Scale Package Using a Modified Coffin-Manson Equation[J]. Microelectronics Reliability, 2004, 44(2): 269-274.

[18] 赵帅帅, 陈永祥, 贾业宁, 等. 基于修正Coffin-Manson模型的加速寿命试验设计与评估[J]. 强度与环境, 2013, 40(4): 52-58.

ZHAO Shuai-shuai, CHEN Yong-xiang, JIA Ye-ning, et al. Design and Assessment of Accelerated Life Testing Based on Modified Coffin-Manson Model[J]. Structure & Environment Engineering, 2013, 40(4): 52-58.

[19] 陈克凡, 乔宏霞, 王鹏辉, 等. 温度循环退化模型的橡胶混凝土可靠寿命预估[J]. 华中科技大学学报(自然科学版), 2020, 48(2): 42-46.

CHEN Ke-fan, QIAO Hong-xia, WANG Peng-hui, et al. Reliable Life Prediction of Rubber Concrete Based on Temperature Cycle Degradation Model[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(2): 42-46.

[20] 肖坤, 顾晓辉, 彭琛. 基于恒定应力加速退化试验的某引信用O型橡胶密封圈可靠性评估[J]. 机械工程学报, 2014, 50(16): 62-69.

XIAO Kun, GU Xiao-hui, PENG Chen. Reliability Evaluation of the O-Type Rubber Sealing Ring for Fuse Based on Constant Stress Accelerated Degradation Testing[J]. Journal of Mechanical Engineering, 2014, 50(16): 62-69.

[21] 谢可勇, 李晖, 庞明磊, 等. 橡胶压缩永久变形率测定常用标准分析与解读[J]. 高分子材料科学与工程, 2015, 31(5): 93-98.

XIE Ke-yong, LI Hui, PANG Ming-lei, et al. Analysis and Interpretation of Standards Commonly Used for Determination of Compression Set for Vulcanized Rubber[J]. Polymer Materials Science & Engineering, 2015, 31(5): 93-98.

[22] 刘小艳, 吴福迪, 王帮武, 等. 低压缩永久变形导电炭黑/硅橡胶复合材料的制备与性能[J]. 复合材料学报, 2015, 32(4): 925-932.

LIU Xiao-yan, WU Fu-di, WANG Bang-wu, et al. Preparation and Properties of Low Compression Set Conductive Carbon Black/Silicone Rubber Composites[J]. Acta Materiae Compositae Sinica, 2015, 32(4): 925-932.

[23] 王莉, 顾晓辉, 潘守华. 某O型密封圈的双参数加速退化规律分析[J]. 装备环境工程, 2019, 16(11): 84-89.

WANG Li, GU Xiao-hui, PAN Shou-hua. Regular Pattern of the O-Ring’s Two-Parameter Accelerated Degradation[J]. Equipment Environmental Engineering, 2019, 16(11): 84-89.

[24] 王丽琴, 鹿忠刚, 邵生俊. 岩土体复合幂-指数非线性模型[J]. 岩石力学与工程学报, 2017, 36(5): 1269-1278.

WANG Li-qin, LU Zhong-gang, SHAO Sheng-jun. A Composite Power Exponential Nonlinear Model of Rock and Soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(5): 1269-1278.

[25] 孙权, 周星, 冯静, 等. 寿命分布的参数Bootstrap拟合优度检验方法[J]. 国防科技大学学报, 2014, 36(6): 112-116.

SUN Quan, ZHOU Xing, FENG Jing, et al. Goodness-of-Fit Test for Life Distributions Based on Parametric Bootstrap[J]. Journal of National University of Defense Technology, 2014, 36(6): 112-116.

[26] CRUZADO A, LUCARINI S, LLORCA J, et al. Microstructure-Based Fatigue Life Model of Metallic Alloys with Bilinear Coffin-Manson Behavior[J]. International Journal of Fatigue, 2018, 107: 40-48.

[27] HAPPONEN T, RITVONEN T, KORHONEN P, et al. Modeling the Lifetime of Printed Silver Conductors in Cyclic Bending with the Coffin-Manson Relation[J]. IEEE Transactions on Device and Materials Reliability, 2016, 16(1): 25-29.

Life Evaluation Method of O-type Rubber Seal Ring Based on Cyclic Impact Acceleration Test

WANG Yan-yan, QIN Chao-xuan, ZHAO Fang-chao, ZHU Hao-ruo

(Southwest Institute of Technology and Engineering, Chongqing 400039, China)

The work aims to quickly and accurately evaluate the storage life of O-type rubber seal ring under temperature cycling condition. Special fixtures were designed to simulate the real compression condition of O-type rubber seal ring. The degradation data of seal ring were obtained by temperature cycling impact acceleration life tests under four stress conditions. The false failure life of seal ring was analyzed and obtained. The modified Coffin-Manson model was constructed and the false failure life data obtained under different test conditions were used to estimate the parameters of the model. Then, the Coffin-Manson life prediction model was obtained, and the storage life of seal ring was extrapolated under normal temperature. The test results showed that the exponential model could describe the degradation of the seal ring more accurately than the logarithmic model and the linear model. After evaluated by Coffin-Manson model, the storage life of the O-type rubber seal ring under normal temperature was 6.13 years, which was in accordance with the engineering experience data. The proposed life evaluation method of O-type rubber seal ring based on cyclic impact acceleration test can accurately evaluate the storage life of seal ring, greatly shorten the test cycle, save the time and cost of life evaluation test, and provide reference value for the life evaluation of seal devices.

seal ring; life evaluation; temperature cycle; acceleration life test; Coffin-Manson model; fixtures

TJ07

A

1672-9242(2023)01-0001-07

10.7643/ issn.1672-9242.2023.01.001

2021–12–10；

2021-12-10；

2022–02–21

2022-02-21

王艳艳（1980—），女，硕士，高级工程师，主要研究方向为产品环境适应性评价。

WANG Yan-yan(1980-), Female, Master, Senior engineer, Research focus: product environmental worthiness evaluation.

王艳艳, 秦朝轩, 赵方超, 等. 基于循环冲击加速试验的某O型橡胶密封圈寿命评估方法[J]. 装备环境工程, 2023, 20(1): 001-007.

WANG Yan-yan, QIN Chao-xuan, ZHAO Fang-chao, et al.Life Evaluation Method of O-type Rubber Seal Ring Based on Cyclic Impact Acceleration Test[J]. Equipment Environmental Engineering, 2023, 20(1): 001-007.

责任编辑：刘世忠