水平管流中水合物颗粒运移和沉积数值模拟

冯明 FENG Ming

（中海石油（中国）有限公司海南分公司，海口 570100）

0 引言

水合物流动保障问题已成为制约深水油气开发的关键问题之一[1]。深海浅部地层具有低温高压环境，容易在生产管柱中生成水合物，沉积并附着在管壁上，导致井筒出现水合物堵塞风险。研究水合物颗粒的运移和沉积规律对探究水合物堵塞的机理具有重要意义。

Lingelem等人（1994）提出了天然气主导体系中水合物生成沉积的概念机理，在初始结晶阶段，水分子和气体分子分散在冷管管壁，形成亚临界核，进而生长为晶体；随着水分子与气体分子不断扩散，晶体持续生长，最终形成水合物堵塞[2]。Turner等人（2005）针对气液共存系统建立了水合物动力学模型：CSMHyK模型，将过冷度和气液接触面积考虑在内[3]。Jassim等人（2010）使用CFD技术模拟了单水合物颗粒沉积的实验，并提出了一种计算气主导系统中单水合物颗粒沉降的理论模型[4]。Di Lorenzo等人首次对管道内环形雾流中的水合物形成和输送进行了室内实验研究，并获得了大量实验数据，如水合物形成速率、管壁上的水合物层生长速率等[5]。Wang等人讨论了环雾流中的水合物沉积特征，并初步发现，气芯中液滴产生的水合物颗粒和管壁液膜处产生的水合物颗粒均会沉积并粘附在管壁上[6]。

目前少有研究关注水合物颗粒在气相中在管壁附近的运动状态。本文利用优化的DPM模型模拟了水合物颗粒在气芯中的运移和沉积特征，得到了水合物颗粒的运移和沉降特征，为准确预测水合物沉积堵塞提供了理论依据。

1 求解模型

气井井筒以环雾流为主，气相连续分布，液相以管壁液膜与气核液滴形式存在，两种形式均为水合物生成创造了条件，如图1所示。研究该体系水合物沉积机理，必须综合考虑液膜与气核液滴中颗粒群的沉积。液膜中由于自由水存在，颗粒与壁面间的粘附力很大，水合物将直接沉积于壁面，前人对此研究做的工作较充分，本文主要针对气核液滴中的水合物颗粒沉积机理展开研究。

图1 环雾流体系水合物颗粒沉积示意图

本文采用的数值模型主要是离散相模型（DPM），颗粒力平衡方程的形式由公式（1）表示，该式右边第一项为颗粒单位质量力，第二项是重力项，第三项是粒子其他力[7]，水合物颗粒受力示意图见图2。

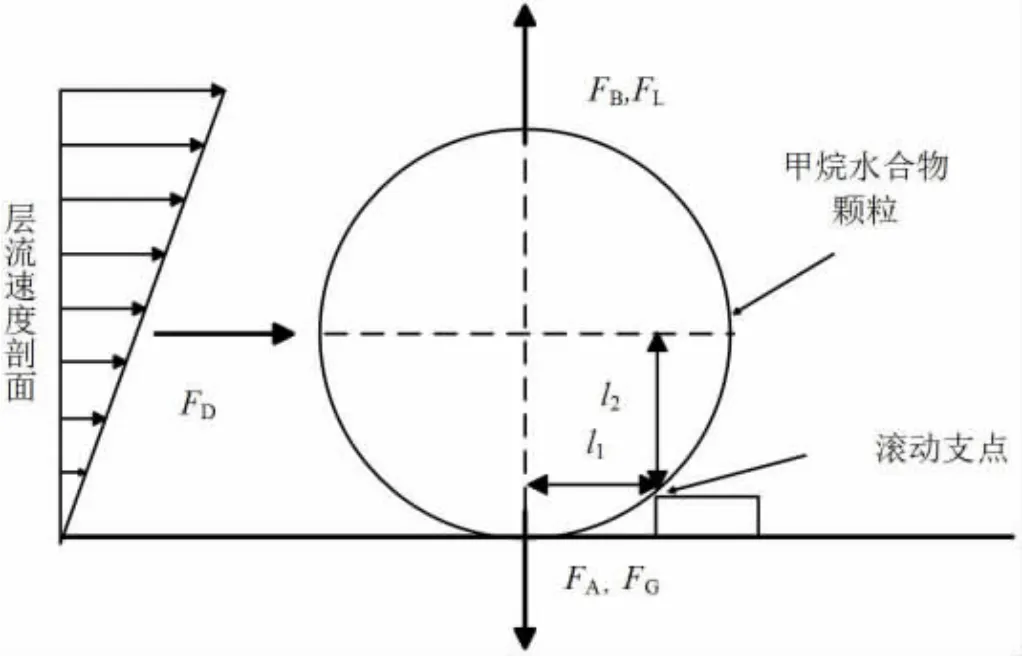
图2 水合物颗粒在管壁上的应力状态示意图

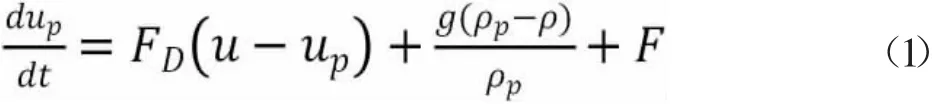
阻力FD可以通过公式（2）计算[8]。

当颗粒在近壁面移动时，流场变化以及壁面与颗粒间相互作用使颗粒受到萨夫曼升力和壁面粘附力的影响。由于壁面附近的流体速度梯度大，萨夫曼升力将对粒子运动产生很大影响，可通过下式[9]计算。

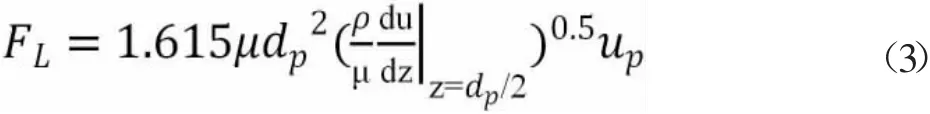
颗粒与壁面间的粘附力是两个物体之间所有分子和原子吸引力的总和，计算方法见下式[9]。

先前的研究发现，颗粒旋转是水合物颗粒沉积在壁上的关键因素。G.M.Burdick等人通过引入临界颗粒雷诺数，定量表征了水合物颗粒在壁上的运动特性[10]。如果雷诺数大于临界值，粒子将离开壁面。所建立的水合物颗粒沉积判断标准如下式：

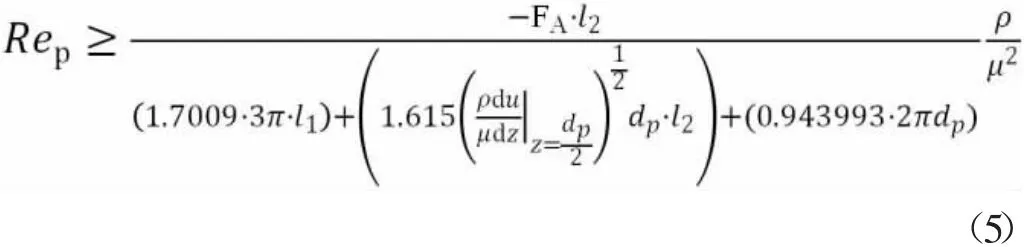
2 数值求解过程及结果分析

2.1 模拟方法和参数

模拟中使用的物理模型是长度为1.5m、直径为0.1m的圆柱形管道。网格采用O-grid网格法划分。气体成分为纯甲烷，液体含量为5%，气体流速为15m/s，液体流速为0.08m/s。本研究采用瞬态模拟，使用欧拉-拉格朗日方法。由于颗粒的湍流扩散对颗粒轨迹方程的求解有很大影响，因此在该模拟中考虑了颗粒对连续相的影响。首先，利用k-ε模型得到收敛的连续相流场，然后建立离散相模型进行耦合计算。

2.2 结果和分析

本节以管径0.15m，气速15m/s，粒径0.3mm模拟结果为例，对模拟结果进行分析。图3为不同气体速度下水合物沿管道轴向的浓度分布，水合物颗粒浓度主要集中在管道后部，最大颗粒浓度集中在管道底部。这是因为颗粒在管流中的径向运动主要受重力的影响。同时，气速越大，气体对水合物颗粒施加的剪切力越强，因此水合物颗粒在壁上的浓度分布越小，水合物颗粒分布也越均匀。

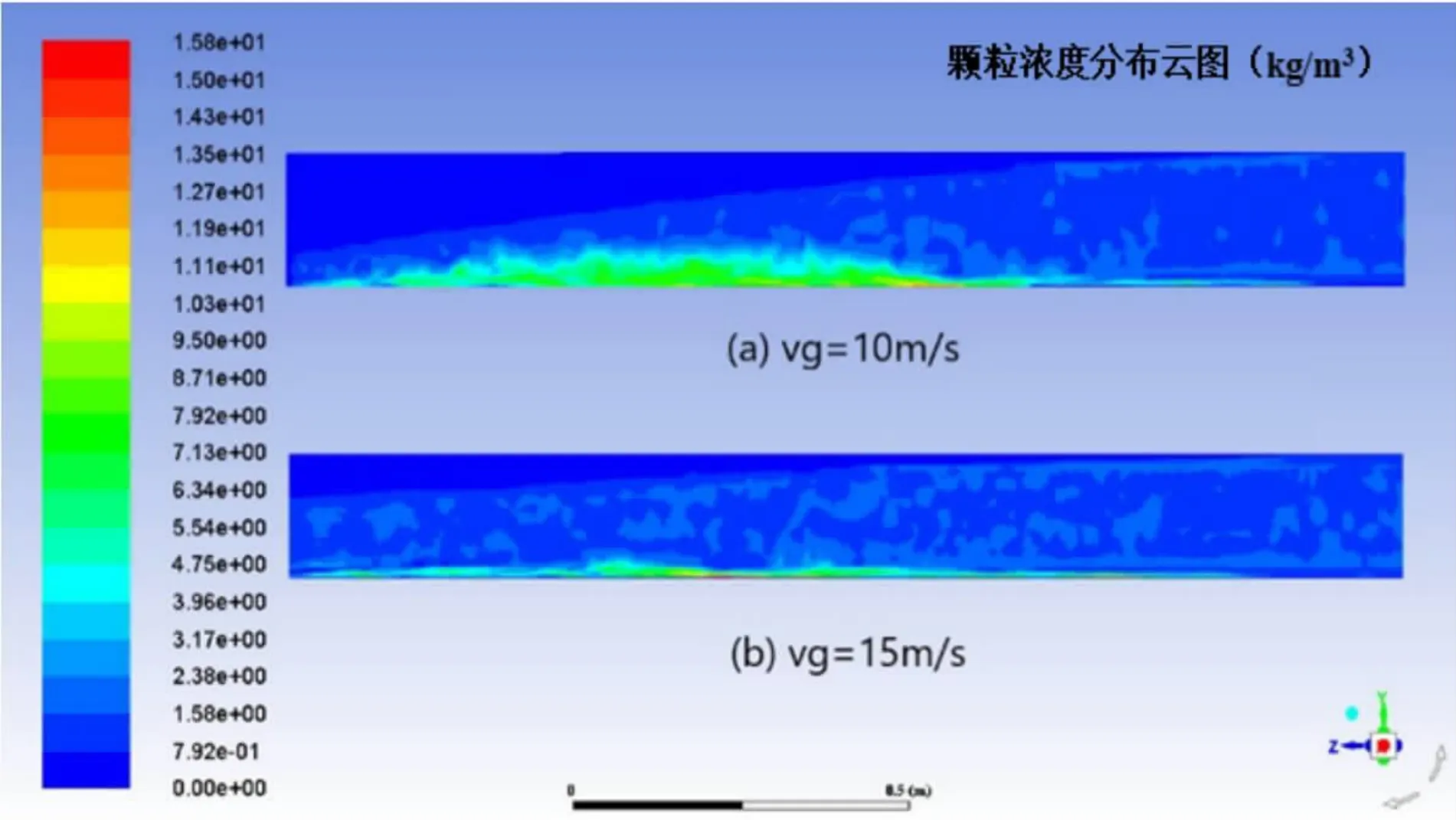
图3 不同气体速度下的颗粒浓度分布

通过捕获壁面上的水合物颗粒，我们获得了注入的颗粒总数和沉积在管壁上的颗粒数量，并计算了气相中水合物颗粒的沉积率。图4为不同气速条件下水合物颗粒沉积率的结果。最大颗粒沉积率可以达到7%左右，沉积率随气体速度的增加而减小，随颗粒尺寸的增加而增加。气速对沉积率的影响体现在两个方面。随着气速增加，流体湍动能越大，颗粒获得的动能增大，使得颗粒的反弹能量更大，因此碰撞后沉积的概率降低；同时气体的剪切效应更强，壁面颗粒在剪切力的作用下更容易返回气流，导致沉积概率降低。

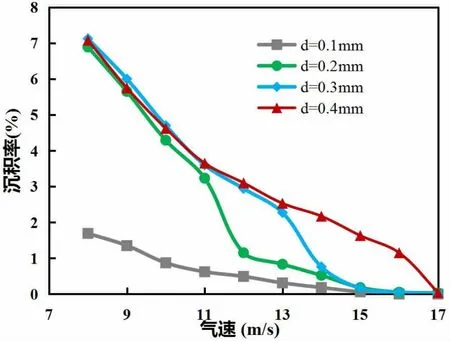
图4 颗粒沉积速率随气体速度和颗粒尺寸的变化曲线

图5表示了不同管径不同粒径水合物颗粒沉积率的变化曲线。粒径较小时，沉积率的变化较大：粒径增大，沉积率明显增大；当粒径增大到临界值时，粒径增大，沉积率几乎稳定。在湍流核心区，颗粒的径向运动主要受重力的影响，重力随粒径增大而增大，气流对颗粒的携带作用减小，颗粒碰撞壁面的数量增加。对于微细颗粒，其壁面的粘附力为其他作用力数量级的几倍，颗粒一旦附着在管壁便很难脱离；而对于大颗粒，由于壁面的粘附力与粒径呈一次方关系，使颗粒脱离的作用力与粒径呈三次方关系，因此颗粒粒径越大，越容易从壁面脱离。因此，当颗粒为小粒径时，粒径越大，运动到壁面的颗粒数越多且易沉积，沉积率会增大；当粒径增大到一定程度，虽然运动到壁面的颗粒数多，但是颗粒二次悬浮的量也会增大，最终会达到一个动态平衡，即粒径增大，沉积率变化幅度不大。

图5 不同管径下水合物颗粒沉积率随粒径变化曲线

3 结论

本文根据水合物颗粒的受力特性，建立了水合物颗粒运移模型和管壁沉积判断准则，并在Fluent中对传统的DPM模型进行了优化，得到了管道中的流场分布和水合物颗粒分布规律，并求解了不同气速、颗粒粒径及管径条件下水合物颗粒沉积率。研究发现，水合物颗粒的运移速度主要表现为气芯内的高速和管壁附近的低速，其运移主要受重力影响。同时气核中水合物颗粒的沉积率约7%，随着气体速度的增加而降低，随着颗粒尺寸的增加表现为先增大后稳定。本研究为准确预测水合物层的生长速度提供了理论依据。

注：

u，up—流体和颗粒速度，m/s；

g—重力加速度，m/s2；

ρp，ρ—颗粒和流体密度，kg/m3；

FD，FL，FA，FG，FB—阻力、Saffman升力、粘附力、重力、浮力，N；

AhmHamaker常数，本文取9.722×10-21；

h—颗粒与管壁间距，本文取14A；

l1，l2—颗粒旋转力臂，m；

μ—动力粘度，N·s/m2；

dp—颗粒粒径，mm；

CD—阻力系数；

Rep—颗粒雷诺数。