岩体力学参数反演的代理蜜獾优化方法
2023-02-11李建合孙伟哲苏国韶
李建合, 孙伟哲, 苏国韶,3*
(1.广西新发展交通集团有限公司, 南宁 530007; 2.广西大学土木建筑工程学院, 南宁 530004; 3.广西岩溶区水安全与智慧调控工程研究中心, 南宁 530004)
交通隧道、引水隧洞或地下发电厂房等地下岩体工程设计与施工中,确定岩体力学参数是一项重要的基础工作。虽然一般岩体力学参数可通过室内试验或原位测试得到,但受尺寸效应和空间分布不均等方面的影响,试验或测试结果与实际情况往往存在较大出入。如何准确合理地确定岩体力学参数一直以来都是地下工程设计与施工中经常遇到的问题,其中,利用反演方法推演岩体力学参数可以较好地解决这一问题[1]。
通过设定目标函数、优化变量与约束条件,将岩体参数确定问题转化为优化问题,借助优化法搜索较优的参数,这类方法称为岩体力学参数优化反演法[2]。由于岩体位移监测较为方便,使得基于位移构建目标函数与约束条件的优化反演法得到了广泛应用[3]。此外,针对单纯形法[4]、共轭梯度法[5]、复合形法[6]等传统优化算法往往难以获得全局最优解的问题,自20世纪90年代以来,遗传算法 (GA)[7-8]、粒子群优化算法 (PSO)[9-10]、差分进化 (DE)[11]、鱼群算法 (IAF)[12]等仿生优化算法被应用于优化反演问题,可以克服传统优化算法的不足。但是,仿生优化算法是一种随机优化算法,对于非凸全局优化问题,往往需要成千上万次地调用目标函数以评价个体的优劣。复杂地下工程的岩体力学参数优化反演中,基于位移变量的目标函数值需要耗时的数值计算才能获得,成千上万次地调用目标函数意味着大量地重复数值计算,导致耗时激增,影响了仿生优化算法的良好应用。近年来,有学者提出采用代理模型替代部分数值计算以降低数值计算调用次数,周正军等[13]提出了土石坝位移反演的响应面遗传算法,显著提高了计算效率;关永平等[14]利用遗传算法优化的BP神经网络(ANN)反演围岩力学参数,取得了良好成效;徐国文等[15]分别采用粒子群优化算法、遗传算法、交叉验证算法与支持向量机代理模型结合进行比较研究,证实了仿生优化算法与支持向量机(SVM)相结合的反演方法的优越性;倪沙沙等[16]在反演土石坝渗流场参数时,利用SVM建立渗流参数与水头之间的非线性关系,并通过PSO算法识别渗流参数,提高了计算效率。但是,上述基于代理模型的优化反演法尚存在着一些局限性,如,ANN模型易出现过度拟合[17-18]、SVM模型的最优超参数难以合理确定[19-20]、代理模型的预测性能过度依赖训练样本设置质量,训练样本的数量与分布设置不佳易导致优化反演陷入局部最优等问题。
针对上述问题,现将高斯过程回归(Gaussian process regression,GPR)机器学习模型作为数值计算的代理模型,将蜜獾仿生优化算法(honey badger algorithm,HBA)作为优化工具,结合三维快速拉格朗日数值计算(FLAC3D)方法,提出岩体力学参数反演的一种代理蜜獾优化方法(HBA-GPR-FLAC3D),以期为复杂地下工程岩体力学参数快速确定提供新的有效手段。
1 HBA和GPR的基本原理
1.1 HBA原理简介
HBA是2021年出现的一种新型仿生优化算法[21]。与已有仿生优化方法相比,HBA具有收敛快、适应度函数调用次数的特点。算法思想源于蜜獾觅食行为特点:为了寻找食物来源,蜜獾要么通过自身嗅觉,要么通过跟随向蜜鸟寻找蜂巢。蜜獾会在猎物周围移动,选择合适的区域搜索猎物的行为称为“挖掘”; 蜜獾借助向蜜鸟的指引直接定位蜂巢的行为称为“寻蜜”,如图1所示。HBA的寻优分为挖掘阶段和寻蜜阶段,在挖掘阶段,通常将算子扩展到较远的区域来保证搜索空间中包含足够的潜在目标,在寻蜜阶段,算子逐步向潜在的目标区域靠拢,进行局部搜索。算法原理详述如下。

图1 蜜獾的觅食行为特点Fig.1 Characteristics of foraging behavior of honey badger
蜜獾算子的位置表达式为
xi=lbi+r1(ubi-lbi)
(1)
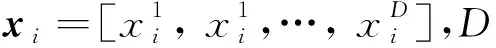
在蜜獾追踪猎物时,蜜獾的追踪强度与猎物的集中强度以及猎物与第i个蜜獾之间的距离有关。HBA中,蜜獾的追踪强度可由反平方定律表示[22],当目标算子集中,或当蜜獾与目标算子之间的距离缩小,蜜獾的追踪强度便会加大,表达式为
(2)
式(2)中:r2为0~1的随机数;S为目标算子的集中强度;di为第i只蜜獾与目标间的距离;xprey为猎物的位置。
密度因子α通过控制随时间变化的随机化,从而确保从全局搜索到局部搜索的平稳过渡。使用式(3)更新随迭代而减小的递减因子α,以减小随时间变化的随机化,表达式为
(3)
式(3)中:tmax为最大迭代次数;C为大于等于1的常数(默认为2)。
在挖掘阶段,蜜獾主要依赖于猎物的气味强度I、蜜獾与猎物之间的距离di和时变搜索影响因子α,此外,控制值F也是使蜜獾能够更好地找到猎物位置的重要因素。蜜獾的动作为如图2所示的心形,其运动轨迹可由式(4)模拟获得,即
xnew=xprey+Fβxprey+Fr3αdi×
|cos(2πr4)[1-cos(2πr5)]|
(4)
式(4)中:xprey为当前目标算子的最佳位置,即全局最佳位置;β一般取6,表征为蜜獾获得食物的能力;di为猎物与第i只蜜獾的距离;r3、r4和r5为0~1的随机数;F为改变搜索方向的控制值,表达式为
(5)
在寻蜜阶段,蜜獾跟随向蜜鸟到达蜂巢的动作可通过式(6)模拟得到,即
xnew=xprey+Fr7αdi
(6)
式(6)中:xnew为蜜獾的新位置;F和α分别由式(5)和式(6)确定;r7为0~1的随机数。
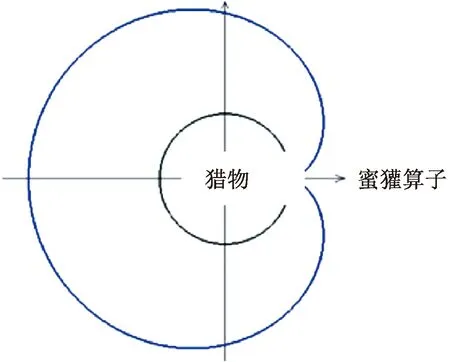
蓝色轮廓表示气味强度;黑色圆形线表示猎物位置图2 挖掘阶段Fig.2 Digging phase
1.2 GPR原理简介
GPR是一种基于贝叶斯理论的机器学习方法,具有非参数和概率性的优点[23-24],可定义为任意有限数量的具有联合高斯分布的随机变量的集合,即高斯过程完全由均值函数m(x)和协方差函数kf(x,x′)确定,表达式为
f(x)~GP[m(x),k(x,x′)]
(7)
对于回归问题,设输出为隐式函数f(x)与高斯噪声ε的和,即
y=f(x)+ε
(8)

(9)
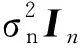
对于与训练集x具有相同高斯分布的新数据集x*,y与预测值y*的联合先验分布为
(10)
采用贝叶斯公式可导出相应的后验分布为
(11)
式(11)中:
(12)
cov(y*)=Kf(x*,x*)-Kf(x,x*)T·
(13)
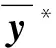
常用的协方差函数有平方指数协方差函数,表达式为
(14)
式(14)中:σf为函数变化垂直尺度的信号方差;σn为噪声方差;l为长度尺度。超参数集θ[σf,l,σn]可由最大似然法确定[25]。
2 岩体力学参数反演的HBA-GPR-FLAC3D法
2.1 基本思路
优化反演就是通过迭代计算搜索最佳参数组合,使位移计算值与位移实测值尽可能接近的方法,为此可设置反演目标函数[24,26]的表达式为
(15)

研究发现,采用HBA进行优化时,与挖掘阶段的全局寻优相比,寻蜜阶段的局部寻优的适应度函数评价次数明显较多,因此,提升反演效率的关键在于如何显著降低局部寻优过程中的适应度函数评价次数,即减小FLAC3D调用次数。为此,在HBA全寻优过程中,将有最优潜力的局部区域内的算子信息作为训练样本训练GPR,可获得目标函数在某个局部区域范围内的代理模型,为了加快局部寻优,将GPR代理模型作为适应度评价工具,采用牛顿法进行局部寻优,获得当前最优算子的预测值,并调用FLAC3D计算获得当前最优算子的真实适应度。这样处理能显著减少局部寻优过程中的FLAC3D调用次数,有效提高算法的寻优效率。
提出的岩体力学参数反演的HBA-GPR-FLAC3D方法基本思路如下:首先,随机生成携带岩土力学参数的初始化算子,并通过有限差分软件FLAC3D进行目标函数的适应度评价,得到初始算子的适应度值;随后,利用HBA的优化策略对算子进行不断的迭代优化,同时通过FLAD3D对算子进行适应度评价,在优化的过程中,判定当前最优算子是否满足收敛准则,若满足,则停止迭代并输出结果;反之,则继续进行下一步迭代。
2.2 关键技术
2.2.1 采用GPR建立当前最优算子局部邻域的近似目标函数
蜜獾优化算法首先在模型空间内产生初始化算子并进行真实的目标函数适应度评价,经过几轮全局寻优组建寻优经验数据集。之后,选取当前最优算子较近的多个算子构建成局部寻优训练数据集,采用GPR对数据集中的样本进行拟合,从而建立表达决策变量与目标函数值之间的映射关系的代理模型。
2.2.2 针对代理模型的局部寻优加速
采用牛顿法基于GPR代理模型所求取的一阶导数和二阶导数对局部最优解进行拟合,从而求取局部最优解。在全局寻优过程中,将寻优过程中的局部最优解代入真实适应度函数进行一次真算,再将其与当前最优解的真实适应度函数进行比较,如优于当前最优解,则用其替代当前最优解,并标记周边区域为当前最优区域,从而为下一迭代步的局部寻优提供指引。
2.2.3 动态更新局部寻优数据集
在全局寻优过程中,构建一个包含所有算子信息的历史数据集,该数据集记录算子在寻优过程中所有的历史位置与相应的适应度值。在局部寻优前,以该历史数据集为基础建立寻优数据集。提出了一种动态更新寻优数据集的方式,以历史最优算子为中心,选取离中心最近的蜜獾算子构建局部寻优数据集,如图3所示。通过保持数据集的蜜獾算子总数不变,适时调整中心点位置,从而提高GPR代理模型在寻优过程中的预测能力。
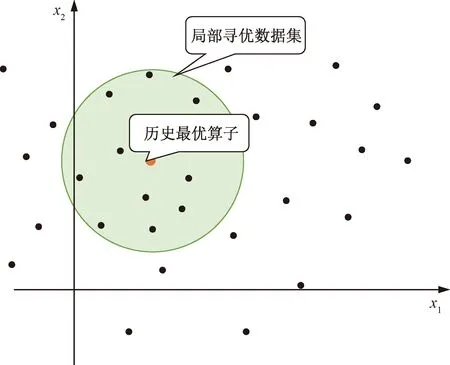
图3 局部寻优数据集的二维模型Fig.3 A 2D model for local optimization datasets
2.3 实现步骤
具体实现步骤如图4所示。
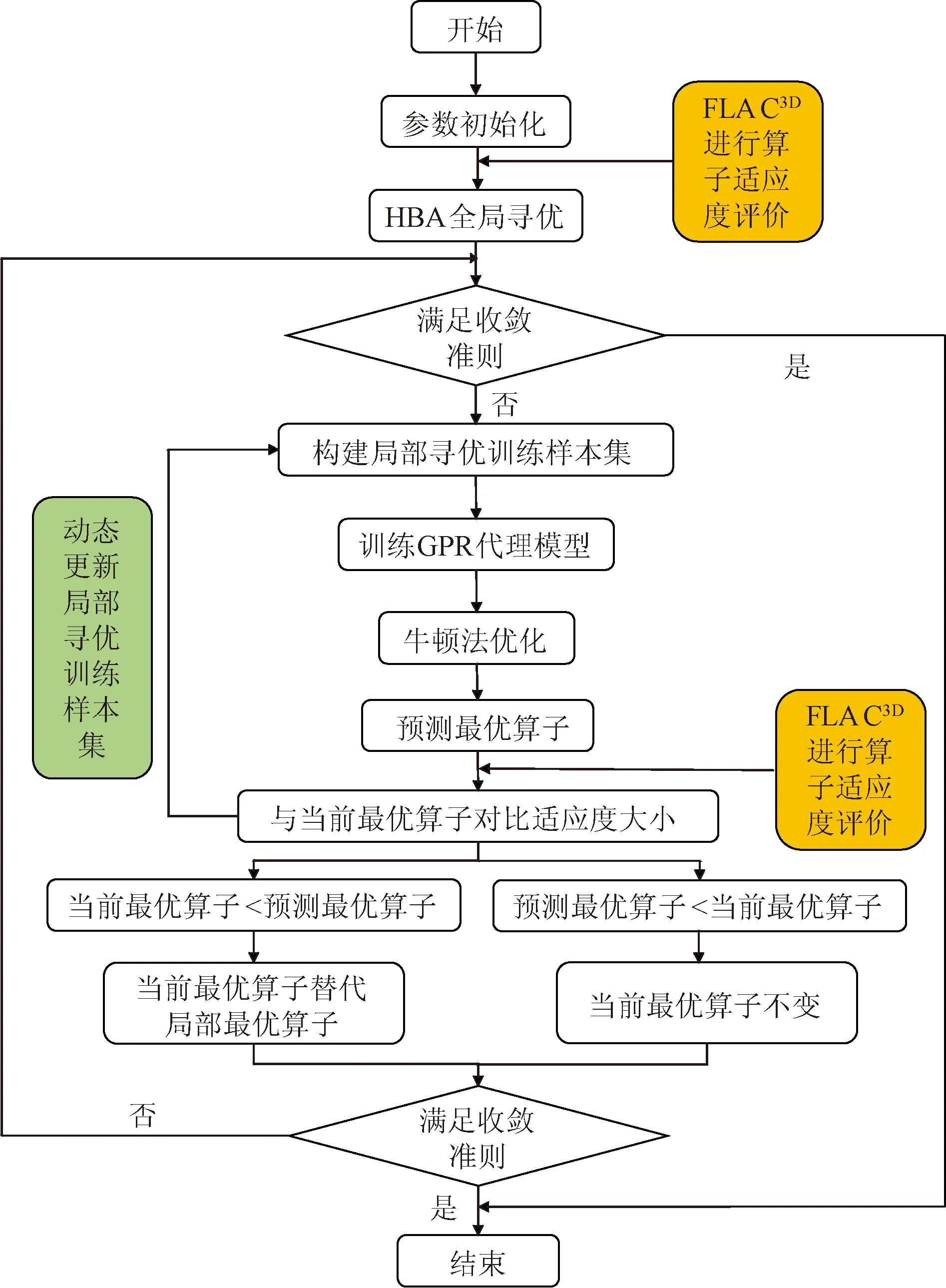
图4 HBA-GPR方法流程图Fig.4 Flowchart of HBA-GPR method
步骤1确定待反演的岩体力学参数及其取值范围,通过FLAC3D建立隧洞的数值计算模型以及选取相应的监测点,将目标函数作为适应度评价函数。
步骤2设置HBA与GPR算法的初始参数;种群数量为N,在求解空间中随机选取N个空间位置作为算子的初始坐标,代入FLAC3D数值计算软件,计算监测点的位移值并代入目标函数,获得相应算子的真实适应度。
步骤3根据HBA算法进行全局寻优,获得当前最优算子;将全局寻优过程中所有算子的坐标及其真实适应度值保存到历史数据集中;判断是否满足收敛准则,若满足,则停止迭代并转至步骤8,否则,转至步骤3。
步骤4以当前最优算子作为中心点,从历史数据集中选取欧氏距离该中心点最近的3N个算子构建成局部寻优训练样本集。
步骤5采用局部寻优训练样本集训练GPR代理模型。
步骤6求解GPR代理模型在当前最优算子点上一阶和二阶导数,采用牛顿法进行局部寻优,获得预测的局部最优算子。
步骤7将预测的局部最优算子坐标代入FLAC3D,计算监测点位移值,获得相应的真实适应度,并添入历史数据集;若预测的局部最优算子真实适应度小于当前最优算子的真实适应度,则将预测的局部最优算子替代当前最优算子,否则,当前最优算子不变。
步骤8判断当前最优算子的真实适应度是否满足收敛准则,若满足,则停止迭代并转步骤8,否则,转至步骤3。
步骤9输出当前最优算子及其真实适应度,结束计算。
3 算例验证
隧洞半径为3.5 m,隧洞沿坐标轴x、z方向围岩厚度均为16.5 m,沿y方向取单位厚度,均质岩性,隧洞的埋深为50 m,围岩容重为20 kN/m3,初始地应力为10 MPa,数值计算模型如图5所示。该模型采用FLAC3D软件推荐的8节点单元,共有1 000个单元体,1 386个节点。越靠近开挖面,网格尺度越小。目标函数设为
(16)

图5 FLAC3D计算网格划分图 Fig.5 Computational grid of FLAC3D
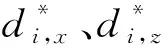
为验证算法可行性,假设真实的岩体力学参数为E=2.2 GPa,c=1.1 MPa,φ=30°。沿着隧洞环向方向分别在0°、22.5°、45°、67.5°、90°处选取5个监测点(如图6所示),采用FLAC3D计算监测点的水平和垂直位移,将其视为“实测位移”,如表1所示。
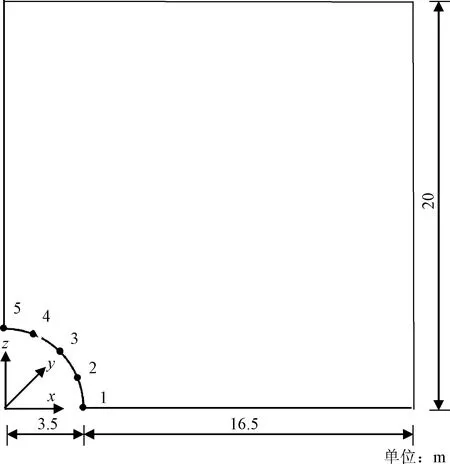
图6 隧洞监测点布置图Fig.6 Layout of monitoring points

表1 各监测点的实测位移值Table 1 The measured displacement of points
采用经典的 Mohr-Colomb 弹塑性本构模型。基于Mohr-Colomb破坏准则的理想弹塑性本构模型是岩石工程领域应用最广泛的本构模型之一。该模型输入参数少,能很好地描述地下工程开挖后的围岩力学,可根据数值计算的网格单元是否进入塑性状态来判断岩体是否发生断裂。
在FLAC3D自带的FISH语言系统中,位移边界的约束主要依赖于速度的约束[27],当单元或节点的速度被约束为0时,位移即被约束。在该隧洞模型中,右侧和底部节点的位移自由度在纵向和竖直方向上都被约束住,以保证模型能顺利收敛。模型的应力边界模拟重力方向的地应力,并通过梯度应力施加到模型上。
分别采用HBA-FLAC3D法与HBA-GPR-FLAC3D法反演该隧洞的岩体力学参数,两种方法中的HBA参数设置均相同:N=50,β=6,C=2。HBA-GPR-FLAC3D法中的GPR模型初始超参数均设置为:lnl=[-1,-1,-1],lnσf=-1,lnσn=ln(1×10-6)。
基于该隧洞的实测岩体力学参数,将反演参数的搜索范围设为:2.0 GPa≤E≤2.4 GPa,1.0 MPa≤c≤1.4 MPa,28°≤φ≤32°,均以目标函数f(X)<5×10-2这一条件作为收敛准则。为了确保上述两种方法对比结果的可信性,降低偶然性的影响,每种算法均进行10次独立运算,取平均适应度评价次数作为每种算法的最终结果。
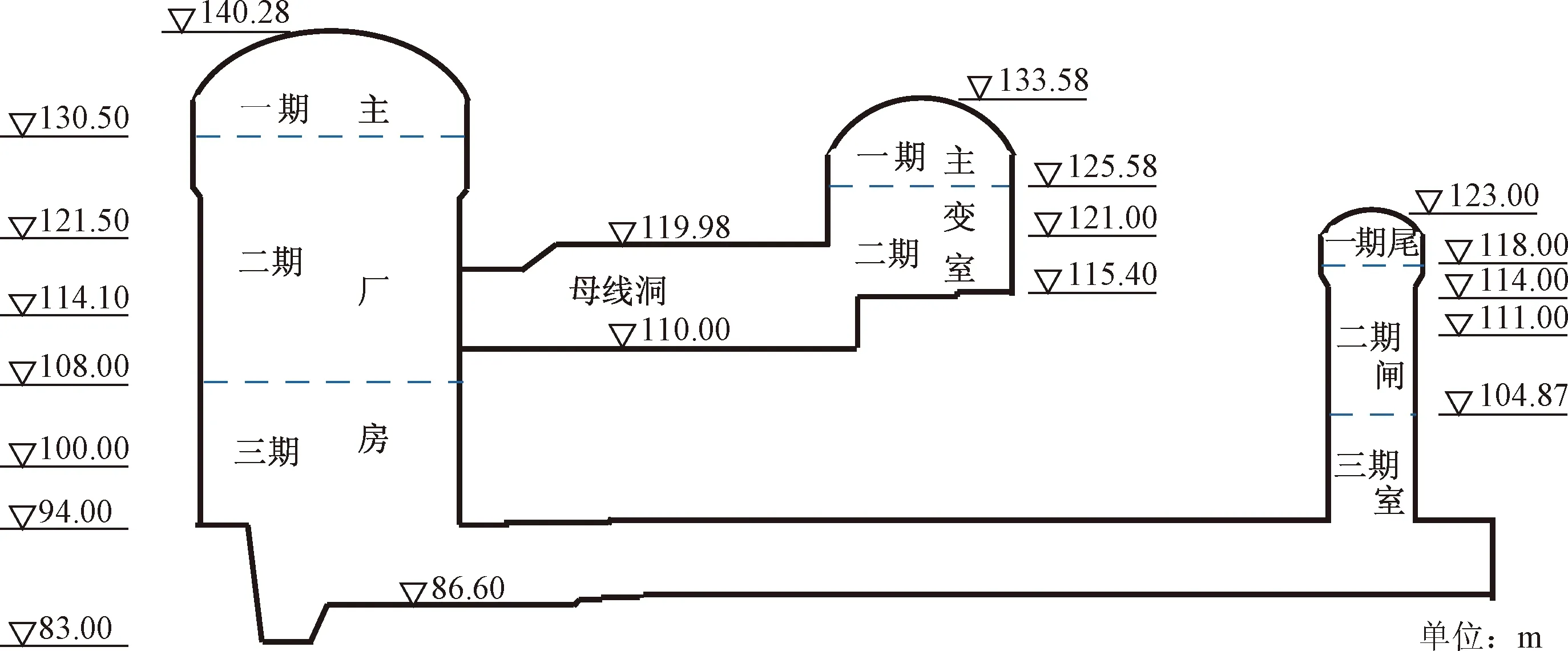
图7 地下厂房分期开挖示意图Fig.7 Schematic diagram of excavation by stages of the power house
计算结果如表2所示,与HBA-FLAC3D法相比,HBA-GPR-FLAC3D法的反演精度较高,但FLAC3D调用次数与计算耗时明显较少,由此说明本文方法的可行性。
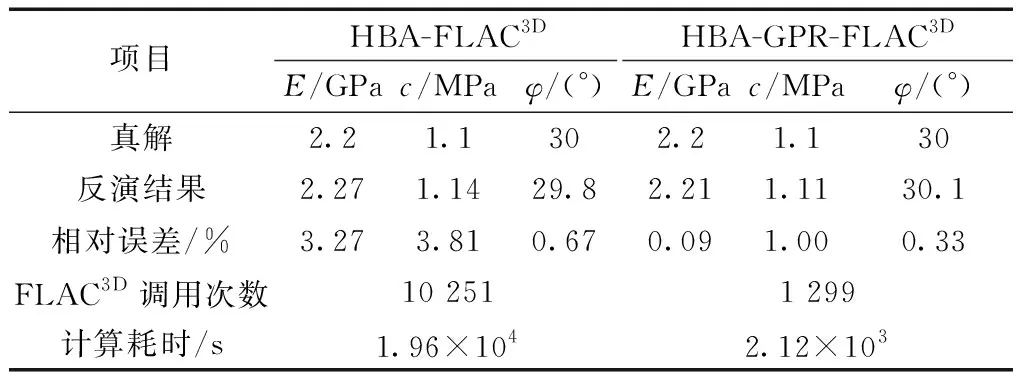
表2 两种算法计算结果对比Table 2 The results calculated by the two methods
4 工程应用
某水电站地下厂房洞室群主要包括主厂房、母线洞、主变室以及尾闸室等大型洞室,围岩主要为Ⅱ、Ⅲ类花岗岩,布置有四台水轮发电机组。主厂房尺寸为180 m×25.9 m×53.675 m,主变室尺寸为164 m×17.5 m×18.175 m,母线洞长度为35 m,分期开挖情况如图7所示。地下厂房共设置了两个位移监测断面,相应监测点布置如图8所示。选取经典弹塑性模型作为其本构模型,根据该本构模型可确定待反演的岩体力学参数包括弹性模量E、黏聚力c和内摩擦角φ。开挖体的数值计算网格如图9所示,数值计算区域为:沿x轴950 m,沿y轴650 m,沿z轴-6~472 m。数值计算网格共使用了687 133个单元和191 323个节点,网格通过不同颜色以区分隧道面积和开挖顺序。由于地下洞室围岩基本为花岗岩,在三维弹塑性数值计算中采用弹脆塑性本构模型[28]。计算采用Mohr-Coulomb强度准则,在建模过程中强度参数(黏聚力c和摩擦角φ)被动态削弱。

图8 位移监测断面Fig.8 The layout map of displacement monitoring points section
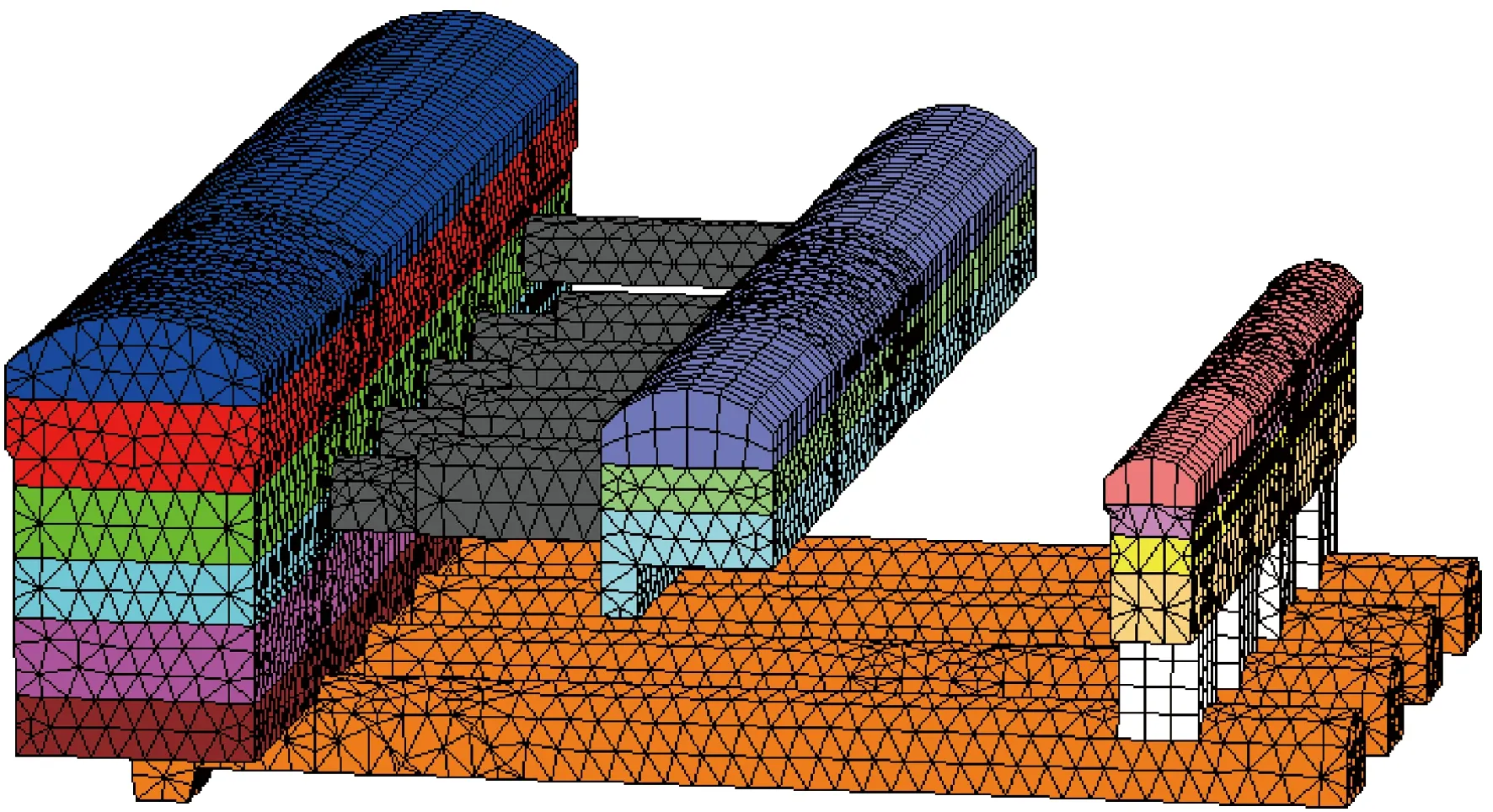
图9 开挖体计算网格Fig.9 The computing grid of excavated rock
相应的监测点布置如图10所示,选择M7、M19以及M24监测点的实测位移构建目标函数,目标函数见式(16)。待反演的岩体力学参数有:主厂房上游围岩弹性模量E1、主厂房1#机组下游围岩弹性模量E2、主厂房2# ~ 4#机组下游围岩弹性模量E3、主变室围岩弹性模量E4、主厂房上游围岩黏聚力c1、主厂房下游围岩黏聚力c2以及内摩擦角φ。参数搜索区间设为:60 GPa≤E1≤80 GPa,10 GPa≤E2≤30 GPa,20 GPa≤E3≤ 40 GPa,100 GPa≤E4≤300 GPa,5 MPa≤c1≤7 MPa,5 MPa≤c2≤7 MPa,40°≤φ≤60°。
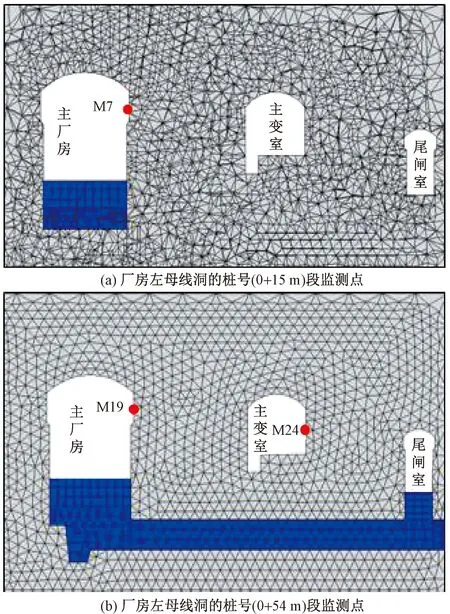
图10 FLAC3D模型中的监测点Fig.10 Monitoring points in the FLAC3D model
经过前期调试工作确定了一种参数组合作为目标函数的最优解:HBA参数设置为N=50,β=6,C=2;GPR模型的初始超参数设置为lnl=[-1,-1,-1,-1,-1,-1,-1],lnσf=-1,lnσn=ln(1×10-6)。以FLAC3D调用次数大于等于1 000作为收敛准则。需要指出的是,所提出的模型参数是适用于弹脆塑性模型的一种参数组合,如果使用另一种本构模型,参数的取值将会相应发生变化,以保证结果的准确性。
分别采用HBA-FLAC3D法与本文方法反演岩体力学参数,结果如表3、表4所示。对于M7、M19监测点,HBA-GPR-FLAC3D方法获得的计算位移值与实测位移值的相对误差仅为1.44%、2.65%,而HBA-FLAC3D方法的相对误差为7.81%、15.72%;对于监测点M24,两种方法的相对误差分别为0.06%、0.73%,差别不大。由此说明,在FLAC3D调用次数达1 000次的相同条件下,本文方法的寻优精度明显高于HBA-FLAC3D,说明了本文方法的先进性。

表3 两种方法的岩体力学参数反演结果
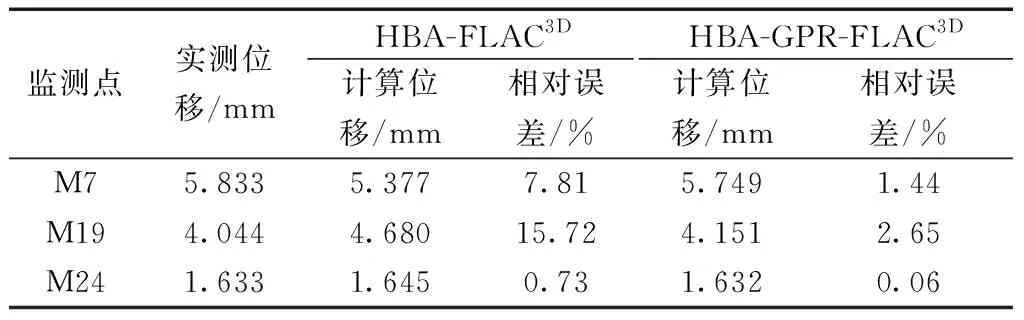
表4 计算位移与实测位移对比Table 4 Comparison of displacements obtained from calculation and measurement
5 结论
针对复杂地下工程岩体力学参数优化反演中获取全局最优解与计算耗时之间的矛盾,提出了一种新的岩体力学参数优化反演方法,得到以下结论。
(1)该方法将强全局寻优能力的仿生优化算法HBA、强拟合能力的GPR机器学习模型以及FLAC3D数值计算有机结合,具有非侵入性、实现简单、易于工程师掌握的特点。
(2)在圆形隧洞算例和水电站地下厂房实例中,分别运用HBA-FLAC3D算法以及本文提出的HBA-GPR-FLAC3D算法进行岩体力学参数的反演计算,结果表明,本文方法在精度和效率上都有着明显优势,适用于单次数值计算耗时大的复杂地下工程岩体力学参数反演问题,为地下工程岩体力学参数快速确定提供了一条有效途径。
由于本文方法的优化结果与蜜獾优化算法、高斯过程回归模型中参数的设置有着直接关系,因此在今后的研究中将探索如何选择合适的参数。
