可再生能源制氢系统多目标优化调度

梁涛， 孙博峰， 刘伟， 王道嵘， 陈丽

(1.河北工业大学人工智能与数据科学学院， 天津 300131； 2. 河北建投能源投资股份有限公司， 石家庄 050011)

人类社会的进步与发展离不开能源，随着传统能源诸如煤、石油、天然气等大量的开采及使用，碳排放量逐年上升，全球各个国家的能源储备量也急剧下降。近年来在碳达峰碳中和政策推行过程中，纯绿色、无碳、无污染且高效方便的氢气得到了大量学者和专家广泛关注。能源低碳化转型是目前能源改革必由之路，而氢能在能源去碳化进程中扮演着越来越重要的地位。使用风光可再生能源这种高效、清洁、低碳的发电方式制备的“绿氢”可以进一步达到降低碳排放量的目的。风能、光能与氢能结合，构成风光互补可再生能源制氢系统，是能源低碳化的典型应用场景[1-3]。

但随着大量分布式发电系统加入电网，可再生能源发电会受到气候因素的影响，这使得电力系统的稳定性降低。研究微电网的调度分配问题使整个可再生能源系统能够实现自我控制、保护以及能量管理，就可以使系统达到提高能源利用率和系统总收益等目的。CPLEX作为混合整数规划的求解器由于可以对于单目标求解问题求解得到最优解而得到了广泛应用，文献[4]提出了一种多时间尺度源储荷协调调度策略，使用CPLEX求解器实现对日前调度计划的修正，提高精确性。文献[5]将最优控制策略和线性混合模型预测控制器应用于制氢系统，考虑系统线性化方程的混合逻辑动态描述，通过以混合整数二次规划的形式求解优化问题来得到控制方法。文献[6]建立电动汽车和需求侧响应协同作用使用CPLEX优化调度模型有效提高了综合能源系统风电、光伏发电消纳能力，降低了系统运行成本。但CPLEX也具有其局限性，在处理多个相互矛盾的目标问题时往往需要引入权重系数转化为单目标问题，这使得整体计算的难度增加，运行时间变长，且难以得到包含所有最优解的帕累托前沿。所以，一些学者使用元启发式算法解决多目标优化调度求解问题。文献[7]使用多目标粒子群算法(multi-objective particle swarm optimization，MOPSO)算法对一个由光伏系统和电池储能系统组成的微电网进行了研究，以达到运营成本和恢复能力之间的最佳平衡。文献[8]提出了一种多目标粒子群优化算法解决最优无功调度问题的方法，求解了含可再生能源和不含可再生能源的电力系统的有功网损和电压偏差目标。文献[9]提出使用改进粒子群算法利用水电输出通道将湖北一梯级水电站与附近风电场、光电场并入电网联合调峰的解决办法。给未来实施梯级水电站与周围风、光电场联合调峰策略提供了参照。但得到广泛使用的粒子群算法[10-11]在搜索效率及算法的寻优能力等多方面有其局限性，使其搜寻最优解的效率和能力较低。

综上所述，目前可再生能源制氢系统的运行调度问题存在一些不足。所以，现以位于河北省崇礼为冬奥场馆氢能大巴提供动力的风光可再生能源制氢系统为研究对象，对建立的系统以总体收益最高、环境成本最低为目标，提出使用搜索能力强、收敛速度快的多目标金鹰算法以小时为单位进行运行优化。选取中国河北省崇礼春夏秋冬四季各一个典型日进行了实验，以CPLEX单目标优化求取的全局最优解为基准，与CPLEX加权求解方法和广泛应用的MOPSO算法求得优化运行结果进行对比，分析所得结果的原因，以此验证所使用方法的可行性并指导实际现场的操作运行，实现“低碳环保，绿色奥运”的理念。

1 模型

1.1 风力发电机组

风力发电机组的基本原理是自然界的风流过风力发电机的风轮，使风轮转动，此过程将自然界的风能转化成了机械能，紧接着风轮经过增速后切割磁感线产生电流继而完成由机械能到电能的转化。风电场的功率输出与风速密切相关，其发电量[12]可以表示为

(1)

式(1)中：Pr为风电机组的额定功率；PWT为风电机组的发电功率；vi为风机正常工作时的切入风速；vr为风机的额定风速；vf为风机正常工作的最大风速。

1.2 光伏发电

光伏发电系统是依靠太阳能光伏电池来进行发电的，通过吸收太阳光来将这种能量储存到太阳能电池板中，它是目前光伏发电中最基本的发电单元，其基本原理是依据光生伏特效应，通过电池板上的半导体材料吸收的太阳能来转化成电能，这种发电原理与PN结二极管类似，即将吸收的光子转化为电子，在内部静电场的作用下，光伏电池的两端会产生电压差，这种效应就被称为光生伏特效应。随着电荷的积累，就会逐渐形成电流，它被称为光生电流，从而获得功率的输出，以实现光到电的转换[13]。

光伏电池的发电输出功率计算公式为

(2)

式(2)中：Ppv为太阳能光伏板实际发电功率；PSTC为太阳能光伏板额定功率；LC为当前环境光照强度；LSTC为理想环境下光照强度，取值为1 kW/m2；μ为功率温度系数；TC为工作时太阳能光伏板表面温度；TSTC为理想环境下太阳能光伏板表面温度。

光伏电池的电流电压是非线性曲线，但是存在极大值点，所以光伏电池的输出功率特性为仅有一个最大输出功率点，并且其值大小受温度和光照强度两个方面因素的影响，并且光照强度和环境温度恒定的情况下，只有使其工作在特定的电压下，才能输出最大功率。

1.3 电解槽

碱性电解槽以KOH水溶液为电解液。在直流电的作用下，水被电解产生氢气和氧气。碱性电解槽于20世纪中期实现工业化。技术成熟，使用寿命可达15年以上。碱性电解槽的结构特点是液体电解质和多孔隔板如图1所示。

碱性电解槽的工作电压模型[14-15]表示如下。

(3)

式(3)中：Uel为碱性电解槽的工作电压；A为电极面积；T为碱性电解槽的运行温度；Iel为碱性电解槽的工作电流；r1、r2为碱性电解槽的内阻；s、t1、t2、t3为电解槽中电极和电解液极化引起过电压的相关参数；Urev为可逆开路电压。

碱性电解槽作为一种特殊的用电设备，具有其特殊性的工作性质。由于电解槽内部材料的特性，电解槽的运行功率不能低于某一限值，否则存在氢气氧气混合发生超过爆炸极限的风险，故需设置其安全工作功率的下限。

图1 电解槽工作原理Fig.1 Working principle of electrolytic cell

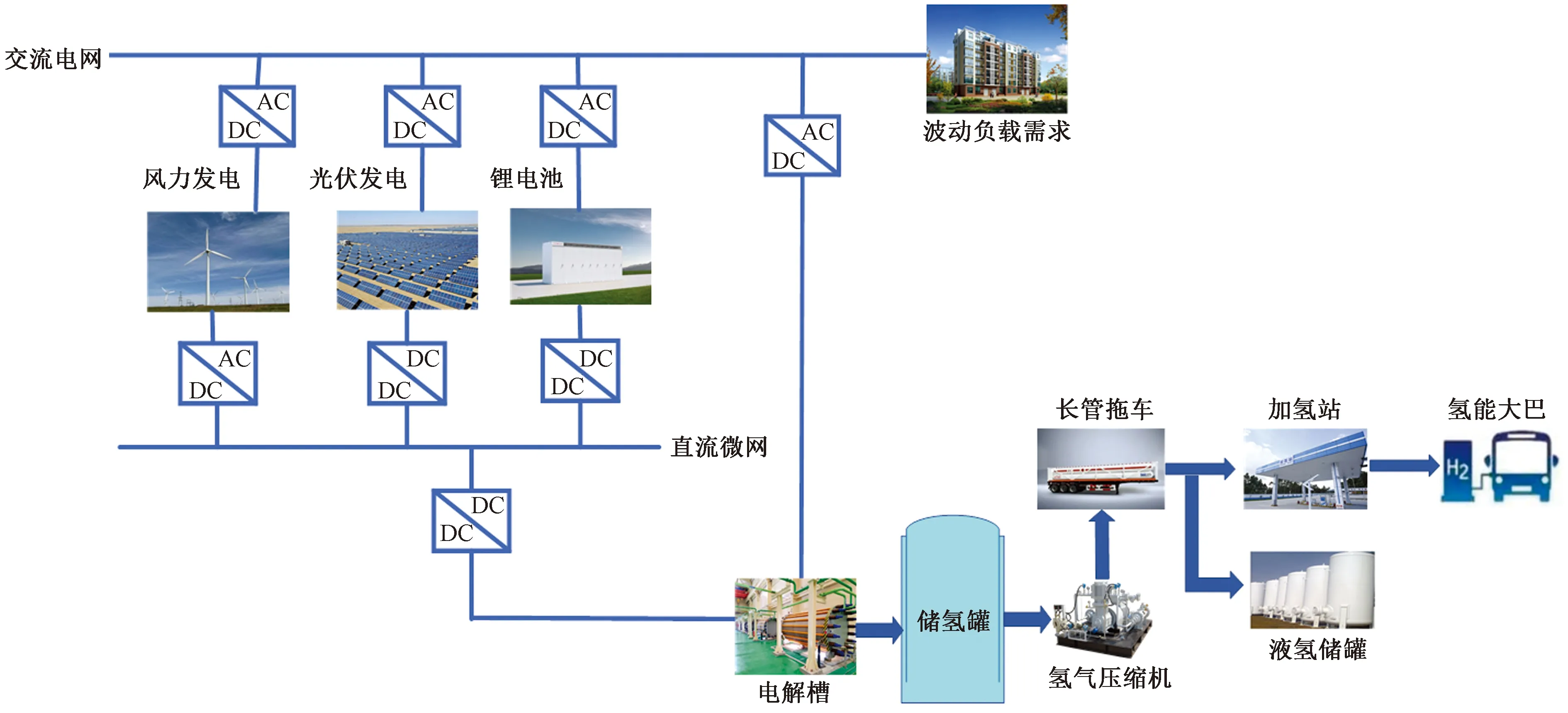
图2 风光互补可再生能源制氢系统Fig.2 Wind-solar complementary hydrogen production system

1.4 锂电池

锂电池具有能量密度大、安全性高、使用寿命长等优点，现在被广泛用于平抑新能源发电功率波动、在电网中削峰填谷以及提高电能质量等，是风光互补可再生能源制氢系统中的重要组成单元。锂离子电池的充放电时的荷电状态可以表示为

(4)

式(4)中：SOC(t+1)、SOC(t)分别为锂离子电池在t+1、t时的荷电状态,Pbat(t)为在单位时间内锂离子电池的充放电功率，充电时值小于0，放电时值大于0；ηdis(t)为锂离子电池的放电效率；ηch为锂离子电池的充电效率；Qr为电池的额定容量。

2 风光互补可再生能源制氢系统

风光互补可再生能源制氢系统如图2所示，系统由风力发电机组、光伏板、锂电池、电解槽、交流母线、直流微网构成。风力发电机组和光伏板作为系统主要的电力来源以满足波动负载需求。由于风光能源产生的电能和负载需求都是随时间与季节波动的，可能会出现风光产生功率无法满足负载需求或风光功率超出负载需求这样不同的负载情况，所以在风光互补可再生能源制氢系统中设计储能装置是必要的。当可再生能源功率过剩时，溢出的电量可以为锂电池充电作为备用电源，也可以为碱性电解槽提供电能电解碱液以完成由电能向氢气转化的电化学过程制备氢气，在实际现场氢气会存入储氢罐中，交由氢气压缩机处理后由长管拖车运输至液态氢储罐或加氢站用于氢能源大巴。当可再生能源不足以满足负载需求且锂电池有足够电能时，可以由锂电池放电为系统供能。当风光资源及锂电池储备电能不足以满足负载需求时可以从电网购电以制备氢气或为锂电池充电，而当可再生能源过剩时，也可以向交流电网售电以获取经济收益。系统实际规模及参数如表1所示。

表1 风光互补可再生能源制氢系统参数Table 1 Parameters of the wind-solar complementary hydrogen production system

3 优化运行过程

从系统运行总收益和环境成本这两个方面综合考虑了风光氢系统的运行优化问题。系统的运行总收益考虑了系统的运行收益包括向电网及负载售电及售氢的收益与系统的运行成本差值。而环境成本则是系统内通过合理调度减少整体系统由于从电网购电而造成的二氧化碳排放。由于售卖氢气收益较高，提高系统收益有时需要通过从电网购电以使电解槽尽可能工作在较大功率，而这与低碳目标背道而驰，所以这是两个相互矛盾的系统优化目标。求解多目标优化问题是求解综合能源系统调度问题的重要方法，相对于单目标优化，它可以对多个优化目标求得最优解集，以解决相互矛盾的目标问题。

3.1 多目标优化问题目标函数

3.1.1 系统运行收益

系统运行收益计算如式(5)所示，主要与系统运行过程中设备维护成本，与电网交换功率收益支出及氢气售卖收益相关。

(5)

(6)

式中：T为系统调度周期内的最大周期数；Igrid为电网收益/支出；Iload为负载供电收益；Ihydrogen为氢气售卖收益；Cequipments为设备维护费用；Csell和Cbuy分别为上网电价及波动电价；Psell和Pbuy分别为系统向交流电网售/购电功率；Pload为波动负载需求；Chydrogen为氢气售价；Phydrogen为实时氢气产量；Cbattery和Cele分别为锂电池和电解槽的维护成本；Pbattery和Pele分别为锂电池和电解槽的工作实时功率。

3.1.2 环境成本

环境成本主要来源于风光氢系统从交流电网购电[16]，由于中国主要电力来源为火力发电，燃煤会产生大量的二氧化碳造成温室效应，所以系统的第二个目标函数设置为最小化系统全天环境成本，表达式为

(7)

3.2 多目标优化问题约束条件

优化问题的约束条件主要包括系统功率平衡约束、设备出力约束、锂电池爬坡约束及电解槽制氢约束。

(1)功率平衡约束。

PWT(t)+PPV(t)+Pbat(t)+Pgrid(t)=Pload(t)+Pele(t)

(8)

式(8)中：PWT、PPV分别为风机和光伏为系统提供的功率；Pbat为锂电池的工作功率可正可负，正值代表锂电池放电，负值则代表锂电池充电；Pgrid为电网的购售电功率，正值代表从电网购电，负值则代表有多余的电量向电网出售；Pload为负载需求电量；Pele为电解槽工作功率。

(2)风机功率约束。

(9)

(3)光伏功率约束。

(10)

(4)锂电池容量约束。

(11)

(5)锂电池爬坡约束约束。

(12)

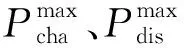
(6)电网购售电交换约束。

(13)

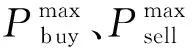
(7)电解槽工作功率约束。

(14)

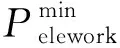
3.3 基于MOGEO的优化调度方案

近年来，应用元启发式技术解决多目标优化问题的研究逐渐受到关注，多目标算法及其改进算法被广泛应用于众多领域。多目标金鹰算法(multi-objective golden eagle optimizer,MOGEO)[18]是Mohammadi-Balani在2021年提出的通过模仿自然界中金鹰狩猎方法所提出的元启发式算法，金鹰狩猎时沿着螺旋轨迹搜寻，沿着直线路径攻击，它们在狩猎的初始阶段更倾向于巡航，并在最后阶段平稳过渡到更倾向于攻击，但它们在飞行的每一刻都同时保持巡航和攻击的倾向，也能寻找其他金鹰关于猎物的信息。多目标金鹰算法的求解步骤如下。

步骤1初始化金鹰种群，评估适应度函数后，初始化种群记忆，攻击倾向及巡航倾向。

步骤2对每次迭代更新攻击倾向及巡航倾向，计算现有存档群体的拥挤度。

步骤3使用拥挤度加权的轮盘赌策略从档案中随机选择猎物。

步骤4计算攻击向量，若攻击向量不为0，则计算其巡航向量，步进向量并更新位置，评估新位置的适应度；

步骤5如果新位置对档案中群体是非支配的，则通过判断存储库是否溢出，如果没有溢出，则直接在存储库中加入新的解决方案，如果已经溢出，则需要通过使用稀疏距离加权的轮盘赌方式选择被移除的档案成员，用新的方案替换输出的方案。

以系统收益最高及环境成本最小为目标函数，提出了一种基于MOGEO的风光互补可再生能源制氢系统调度方案，如图3所示。

图3 基于MOGEO的优化调度方案Fig.3 Optimized scheduling scheme based on MOGEO

4 实验

为验证所提出的方法的有效性，从2022冬奥会举办地中国河北崇礼某地春夏秋冬四季各选取一典型日，以图2所示风光互补可再生能源制氢系统为算例模型。系统中供电单元为风力发电机组，光伏发电模组及交流电网；储能元件是锂电池；系统使用碱性电解槽电解KOH溶液制备氢气。在山区风光资源充足的条件下,在保证供电可靠性的前提之下，充分地利用可再生能源，通过合理的优化调度，提高整个风光互补可再生能源制氢系统的收益水平同时降低系统从交流电网购电减少碳排放以响应能源低碳化的号召，最后给出各个子系统设备的出力计划。

为针对该系统解决上述优化调度问题，将全天能源优化问题以小时分辨率划分为24个子问题。在能源价格方面，使用分时电价，设置每日23：00—次日7：00为谷段，每日7：00—8：00和11：00—18：00为平段，每日8：00—11：00及18：00—23：00为峰段，其中谷段电价为0.36元/(kW·h)，上网电价为0.35元/(kW·h)；平段电价为0.53元/(kW·h)，上网电价为0.42元/(kW·h)；峰段电价为0.69元/(kW·h)，上网电价为0.49元/(kW·h)。主要设备维护价格参考文献[19],碱性电解槽运行成本取0.022元/(kW·h)；锂电池运行成本取0.005元/(kW·h)；售氢价格为70元/kg。

选取张家口崇礼春夏秋冬4个典型日作为研究对象，分别命名为案例1～案例4，从NASA Prediction of Worldwide Energy Resources数据库中获取气候信息。图4、图5分别展示了该系统1 d中所吸收的风速和辐射强度,输入前文所述模型得到风光功率。

图4 风速Fig.4 Wind speed

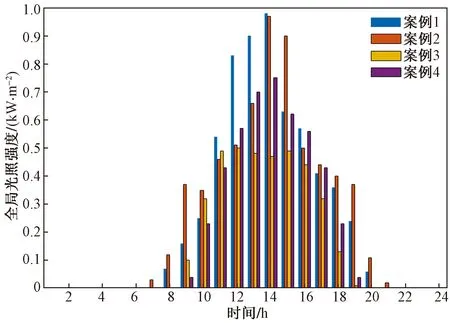
图5 光照强度Fig.5 Global solar

4.1 单目标基准点

CPLEX可以有效地对单目标问题求解出全局最优解。所以使用CPLEX求解器以系统收益最大化及环境成本最小化分别求解以得到单目标问题的最优调度方案，选取案例2为研究对象，分别以系统收益最大化及环境成本最小化为目标函数求取单目标调度方案如图6和图7所示。

由图6、图7可知，由于制备氢气会大幅提高系统收益，所以当设置系统收益最大化为单目标函数时，系统会从电网大规模购电使电解槽工作于额定电压尽可能多地制备销售氢气。反之，当设置环境成本最小化为单目标函数时，由于选取夏季典型日

图6 单目标系统收益最大化Fig.6 System revenue maximization

图7 单目标环境成本最小化Fig.7 Minimum environmental cost

风资源较为紧缺，这也就使得系统在满足波动负载需求后，会尽可能不从电网购电以减小环境成本，这也会导致系统整体收益随之降低。由此可见，系统收益最大化和环境成本最小化是一对相互矛盾的目标函数，单目标优化很难兼顾系统的多个需求以实现同步优化。

4.2 多目标解集

为解决单目标求解所存在的问题，采用多目标金鹰算法，每小时对风光互补可再生能源制氢系统中各模块出力进行优化，得到一天中每小时的各模块出力的帕累托前沿，实验环境为MATLAB2020a，16 G运行内存，处理系统为Windows10的计算机。

进行单目标优化求解问题时，一些场景下会使用CPLEX求解器作为优化求解工具，CPLEX作为单目标优化求解工具与智能优化算法的优势在于其可以得到全局最优解，但当使用CPLEX处理多目标问题时需要设置不同目标函数的权重转化为单目标问题，这样往往难以求解出均匀的解集，且会大幅增加运算时间。为了验证选取电力系统运行优化中传统的多目标粒子群算法和多目标金鹰算法对比，以及以加权方式使用CPLEX求解器进行优化求解。由于两个目标函数数量差距较大，在使用CPLEX求解时首先需要进行归一化操作，然后设置0.01为步长对其进行加权，以上述3种方法分别对系统运行总收益和系统环境成本两个目标函数进行优化。以案例2为例，3种方法得到的多目标调度方案解集如图8所示。可以看出，与传统的多目标粒子群算法相比，多目标金鹰算法在处理风光互补可再生能源制氢系统多目标操作优化时，具有更宽的搜索空间和更均匀的求解分布，解集质量也得了相应的提高，这也验证了选取多目标金鹰算法的优越性。与两种元启发算法相比，加权CPLEX求解可以得到质量更高的解，但解集存在很大程度的重叠，不够均匀。

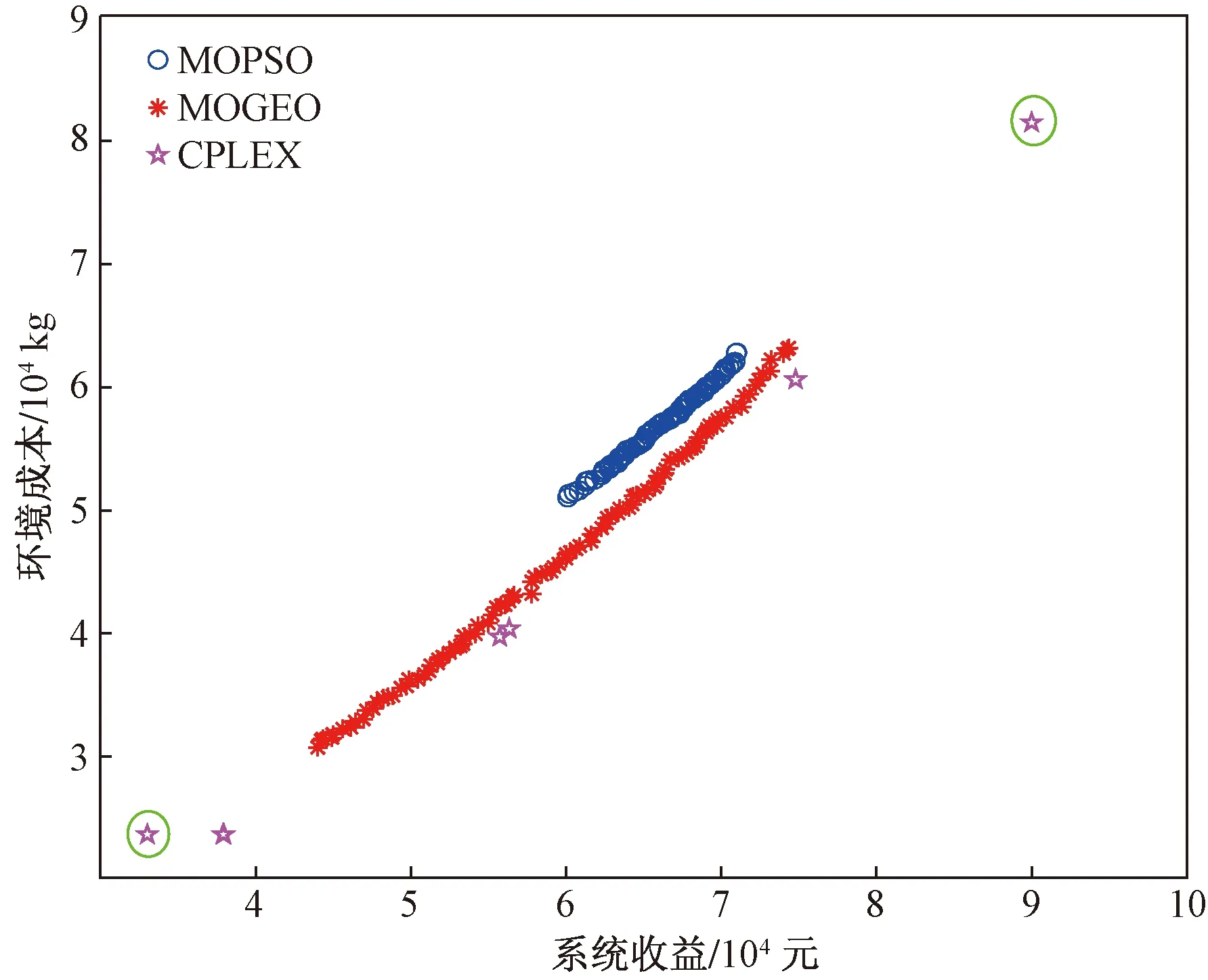
图8 3种求解方法的解集比较Fig.8 Comparison of solution sets of three methods

使用MOPSO算法以收益最大化及最小化环境成本为优化目标函数，设置相同的约束条件在春夏秋冬4个典型日中进行优化计算，选取得到的最优折中解，为方便比较，以系统收益为基准，选取最接近的MOGEO解，以及CPLEX加权方法的折中解。同时将CPLEX所得单目标全局最优结果作为基准进行对比结果如表2所示。通过3种方法求解4个典型日所得最优求解调度方案如图9所示。

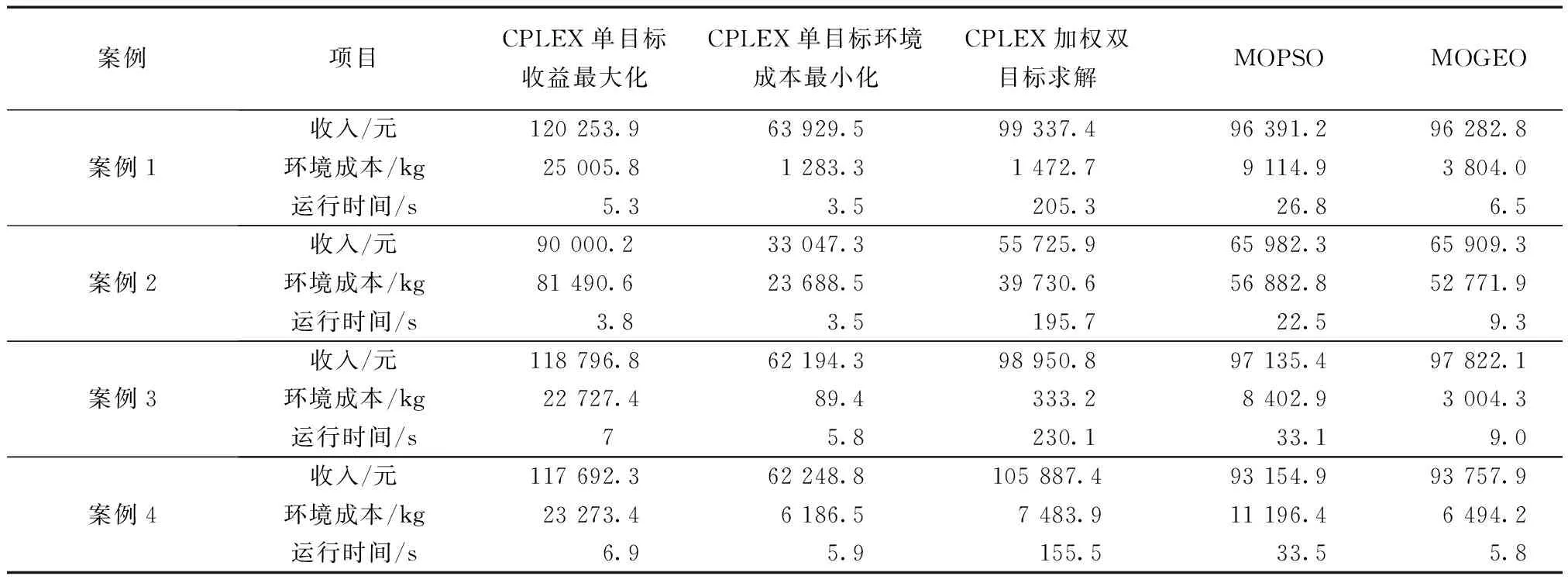
表2 多目标求解结果对比Table 2 Comparison of multi-objective algorithm results

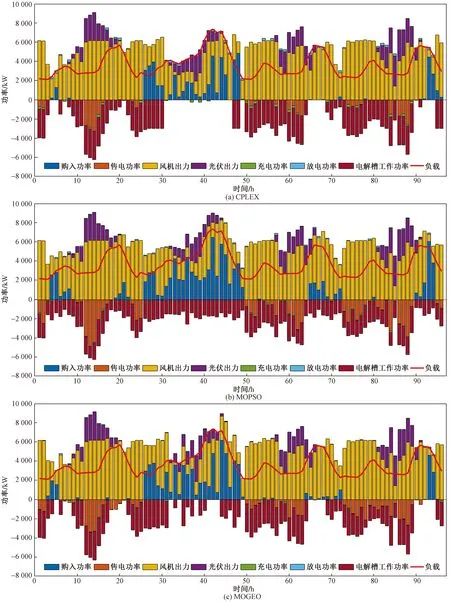
图9 最优折中调度方案对比Fig.9 Comparison of optimal compromise scheduling schemes

结合表2和图9可以看出，3种多目标优化方法都可以有效权衡收益与低碳之间的平衡，在不同情景下，对比与CPLEX单一目标求解的系统收益与环境成本会得到相对较好的折中解。图10展示了3种不同方法在4个案例中的购电情况曲线，由于购电情况可以更为直观地展示系统总体碳排放情况，可以发现，由于在两种元启发算法对比时，选取的折中解以系统收益为基准，所以在大多数情况下，MOGEO优化调度方案中，整体风光互补可再生能源制氢系统可以在收益接近的前提下，大幅减少系统购电量以达到减少环境成本的作用。同时在求解过程中，通过对帕累托前沿和结合表中数据的比较，加权CPLEX方法依然能够得到较高质量的折中解，但尽管如此，这种方法也具有一些缺点，比如解集分布不够均匀，这也就导致了不能提供更多的求解调度方案。而且，CPLEX求解双目标问题时求解时间相较元启发算法大幅提高。结合表2数据和图10，MOGEO算法能够在规模相同的前提下，求得更接近最优解的多目标调度方案解集，且相较加权CPLEX具有更快的求解速度。

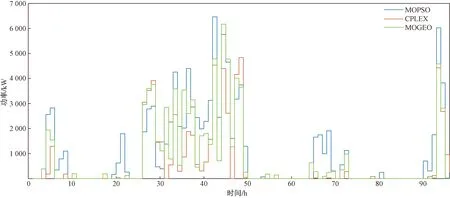
图10 购电情况Fig.10 Electricity purchase situation

由此证明多目标金鹰算法能够在更短的求解时间内，得到分布更为均匀的帕累托前沿以及权衡系统收益最大化与降低环境成本的运行方案。

5 结论

结合风能光能与电解槽构建了一个风光互补可再生能源制氢系统，使用多目标金鹰算法通过合理调度系统内各组件出力以得到以系统收益最大化与环境成本最小化为目的的多目标运行优化方案，并得到如下结论。

(1)提出了一个多目标运行优化模型，通过将风光互补可再生能源系统全天运行优化问题以小时分辨率划分为24个子问题以实现系统运行总收益最大化与环境成本最小化的多目标运行方案。

(2)针对CPLEX混合整数规划求解多目标调度问题的局限性及传统多目标优化算法MOPSO的不足，使用多目标金鹰算法求解优化调度问题，进行4个季节典型日实际调度实验。与CPLEX单目标、多目标加权方法及MOPSO算法对比验证本文方法可以在最大化系统收益的同时兼顾最小化环境成本以减少温室气体排放，对比MOPSO算法该方法可以求得较好解集，又比CPLEX加权求解方法具有更快的求解速度和更好的求解效果，以此为依据可以证明本文方法的优越性。系统实际运行以此为依据指导，以实现“低碳环保，绿色奥运”的理念。