基于多岛遗传算法的垂直轴风机翼型优化设计

赵杰， 汪志成， 邵华梅

(1.东华理工大学机械与电子工程学院， 南昌 330013； 2.江西省新能源工艺及装备工程技术研究中心， 南昌 330013)

垂直轴风力机叶片翼型的优化设计是改善风机气动性能、提升风机风能利用率的有效手段，大致可以分为直接优化法和反设计法两种。直接设计法通常采用梯度优化算法和全局搜索算法来正向求解空气动力学问题；反设计法需要对翼型优化后气动参数建模求解和迭代计算，是一种逆向求解的方法[1]。赖怡等[2]基于模拟退火算法对翼型进行优化设计。Wickramsinghe等[3]使用粒子群优化算法对低速翼型进行研究，开发了一个新的流体评估方案。刘春等[4]对比几种算法对NACA0012翼型气动性进行分析，认为改进的Coupled算法对气动性能预测有帮助。Chen等[5]在考虑了前缘粗糙度敏感性、失速性能等因素影响的情况下，基于粒子群算法构建多目标优化算法。Timnak等[6]基于改进的遗传算法对翼型进行优化设计，计算速度加快并且优化效果更好。Le-Duc等[7]将计算流体动力学(computational fluid dynamics，CFD)方法与改进的遗传算法联合仿真，并在特定条件下对风力机翼型进行了优化研究。余刚等[8]以遗传算法和复合型法为基础，开发并编写流场计算程序，研发了更符合实际应用的翼型优化方法，无论是单点设计还是多点设计，该方法都能提高翼型的气动性能。陈进等[9]构建了多目标翼型优化模型，并采用改进的粒子群算法对初始翼型进行优化，得到的优化翼型的升阻比和升力系数均有所提高。汪泉等[10]采用类函数与B样条结合的翼型参数化表达方法，以切向力系数之和作为优化的目标函数，并使用粒子群算法和气动性能预测软件RFOIL对翼型气动外形进行优化设计，分别从速度分布、功率系数、涡量分布和功率系数这4个方面对优化翼型进行，结果显示优化后的翼型有效提高了力矩系数和功率系数。综上所述，目前研究人员对垂直轴风力机翼型的气动优化进行了大量研究，但对垂直轴风力机翼型依靠CFD方法和全局搜索算法进行气动性能优化研究的分析还不够深入。针对以上问题，现以MATLAB实现参数化程序设计，基于CFD方法中的网格自动生成和流程自动计算技术，结合多岛遗传算法构建翼型目标函数自动优化程序，以期实现基于CFD和遗传算法的垂直轴风力机翼型优化。

1 多岛遗传算法

1.1 多岛遗传算法基本原理

多岛遗传算法(multi-island genetic algorithm，MIGA)是基于遗传算法改进的，比传统的优化算法具有更好的全局求解能力和计算效率。MIGA将整个进化种群再被划分为若干个子种群，被划分的子种群称为“岛屿”，然后对每个岛屿上的子种群分别进行传统遗传算法的遗传算子操作(选择、交叉、变异)，如图1所示。MIGA会每隔一段时间随机选取若干个个体进行“迁移”操作，把这些选中的个体迁移到其他岛屿上，这种迁移操作有效地增强了种群的多样性，从而防止“早熟”问题。此外，MIGA的计算速度高于传统的遗传算法，更加节省研究时间。

MIGA是从遗传算法(genetic algorithm，GA)发展而来的，在参数以及算法的计算流程上基本一致，但MIGA在参数名称和数目上略有区别。MIGA同样采用是适应度函数来评价个体的优劣情况，适应度值大的个体发生繁殖行为的概率较大，这样保持了产生的新群体的平均适应度值高于旧群体。在基因编码方面，MIGA采用格雷码编码，表达式为

(1)

式(1)中：gm为m位的格雷码;bm为m位的二进制码。

种群、选择、交叉和变异操作与传统遗传算法一致，但MIGA的子种群称之为“岛”，并且增加“迁移”操作。具体流程如图2所示。

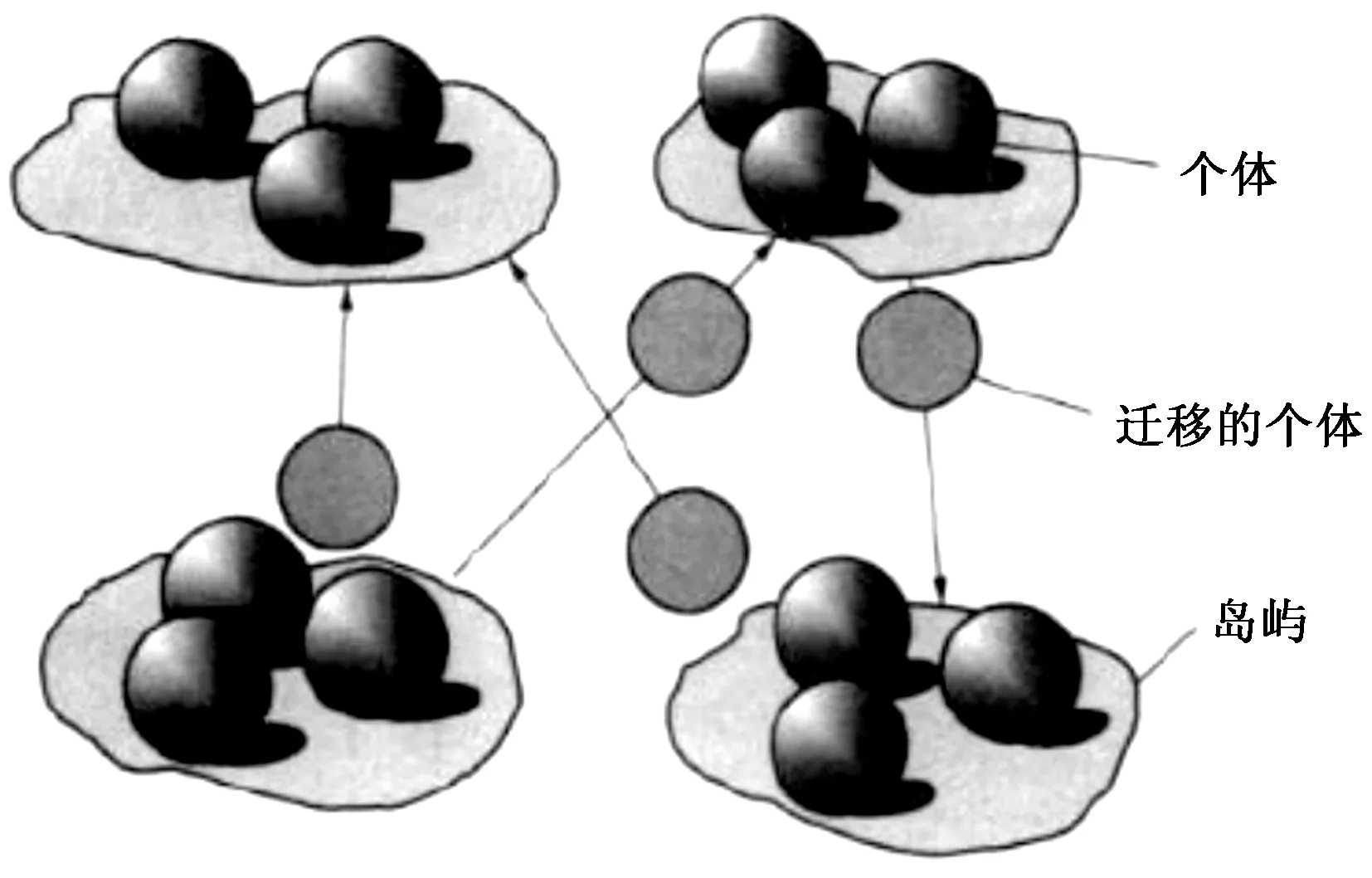
图1 多岛遗传算法示意图Fig.1 Schematic diagram of multi-island genetic algorithm

图2 MIGA相邻两代进化过程Fig.2 The evolutionary process of the two adjacent generations of MIGA

1.2 多岛遗传算法参数

在多岛遗传算法中，有10个参数可以调节，其中3个为基本条件参数，另外7个为高级条件参数。对配置参数进行简单说明如下。

(1)子群规模数。

(2)总体规模数，总体规模数等于子群规模数与岛数的乘积，大的群体规模能够改经GA的搜索的质量。

(3)岛的个数。

(4)进化代数。

(5)交叉概率Pc，顾名思义即表示交叉算子的使用频率。在每一代群体中，需要对Pc×n个个体的染色体结构进行交叉操作。交叉概率与产生新一代的速度有关，通常取值较大，但Pc取值过大会破坏群体的优良模式，过小会导致进化速度过慢。因此，一般取交叉概率Pc为0.6～1.0。

(6)变异概率Pm。变异概率是群体保持多样性的保障，表示个体染色体上基因产生变异的概率，交叉算子结束后，处在繁衍阶段的全部个体的每位等位基因以Pm随机改变，故在每代当中大约会产生Pm×n×L次变异。变异概率同样会影响新一代的产生速度和质量，一般取Pm为0.005～0.01。

(7)岛间迁移率。岛与岛之间种群交换所遵循的比率，一般取值在0～0.5。

(8)迁移间隔代数。即两次迁移之间的间隔。

(9)竞赛子群体比率。从父代的所有子种群中以一定比例随机选择个体进行比较，将种群当中最好的个体保留到下一点。

(10)精英个体数量。即通过竞争后，保留到下一代的最好个体的数量。

在优化研究过程中，对多岛遗传算法的配置参数设计如表1所示，其他参数则按照默认设置。

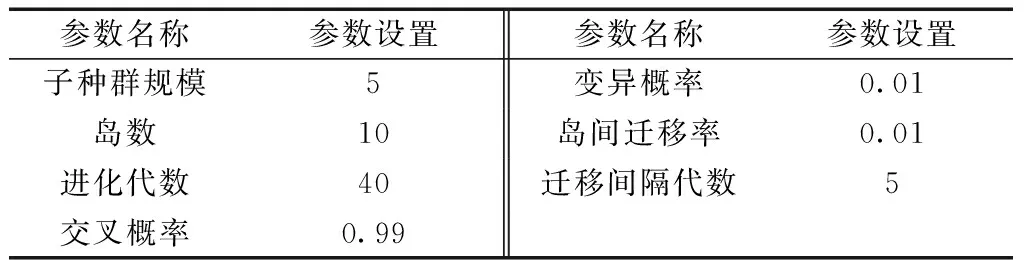
表1 多岛遗传算法配置参数设置Table 1 MIGA configuration parameter settings

2 优化算法设计

以NACA0012作为初始翼型，对风速10 m/s、攻角8°时的翼型进行优化，找出满足该条件下的最大升阻比的最佳翼型轮廓，并分析优化翼型气动性能。

2.1 目标函数

升阻比是风力机叶片性能的重要指标，并且高升阻比的翼型可以在低风速的地区，满足风力机的低风速要求。在优化研究中，以升阻比作为优化设计的目标函数。翼型的优化目标函数为

(2)

式(2)中：Cl、Cd分别为优化翼型的升、阻力系数。

2.2 设计变量

采用Hicks-Henne参数法对翼型轮廓描述，并基于MATALB编写翼型参数化计算程序。本优化以控制翼型形状的系数ci(i=0,1,…,13)为设计变量，通过多岛遗传算法改变设计变量的取值来控制翼型形状的变化。

2.3 约束条件

在翼型的优化约束中，一般分为两种：几何条件约束与气动性能约束。前者主要是指翼型在参数化建模过程中可以修改翼型轮廓曲线的相关控制参数的取值范围；后者则是指翼型的气动性能相关参数，如升阻比、升力系数、阻力系数等，具体的约束需要更具翼型的设计要求来确定。优化设计中主要约束包括：设计变量的取值范围约束；初始翼型升、阻力系数的约束。优化设计中的变量约束范围如表2所示。

表2 设计变量ci取值范围Table 2 Value range of design variable ci

此外，优化翼型的升、阻力系数需要满足以下条件。

(3)

式(3)中：Cl0和Cd0为原始升、阻力系数。经数值模拟计算结果，Cl0=0.808 0，Cd0=0.021 8。

2.4 优化设计程序

优化设计程序是以多岛遗传算法作为核心算法来计算目标函数值的。如图3所示，开发了用于优化的自动目标函数评估流程，该流程将翼型参数化、网格生成和目标函数评估与CFD仿真相结合。采用宏命令，顺序调用所有软件。自动优化过程开始于在多岛遗传算法中生成14个控制变量，即Hicks-Henne型函数的控制系数。然后基于该型函数的参数化，生成新的翼型轮廓数据点并保存到脚本文件中。利用ICEM的网格自动生成技术完成每一次修改后翼型形状的网格生成，以便在Fluent中调用日志文件进行流场自动计算。接着对数值计算结果进行后处理以计算翼型的升、阻力系数及升阻比。最后，如果满足全局最优解，则评估过程终止；否则，遗传算子会产生的一组新的变量重复这个过程，自动优化重复执行。

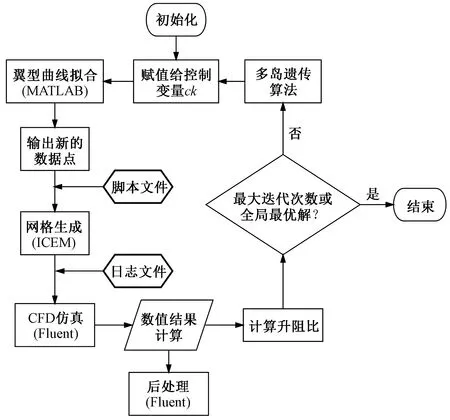
图3 自动优化评估过程Fig.3 Automatic optimization evaluation process

3 优化结果分析

3.1 翼型几何轮廓

以升阻比为目标函数的优化研究，如图4所示，经过40代的计算得到了收敛的优化结果，设计变量的最终取值如表3所示。

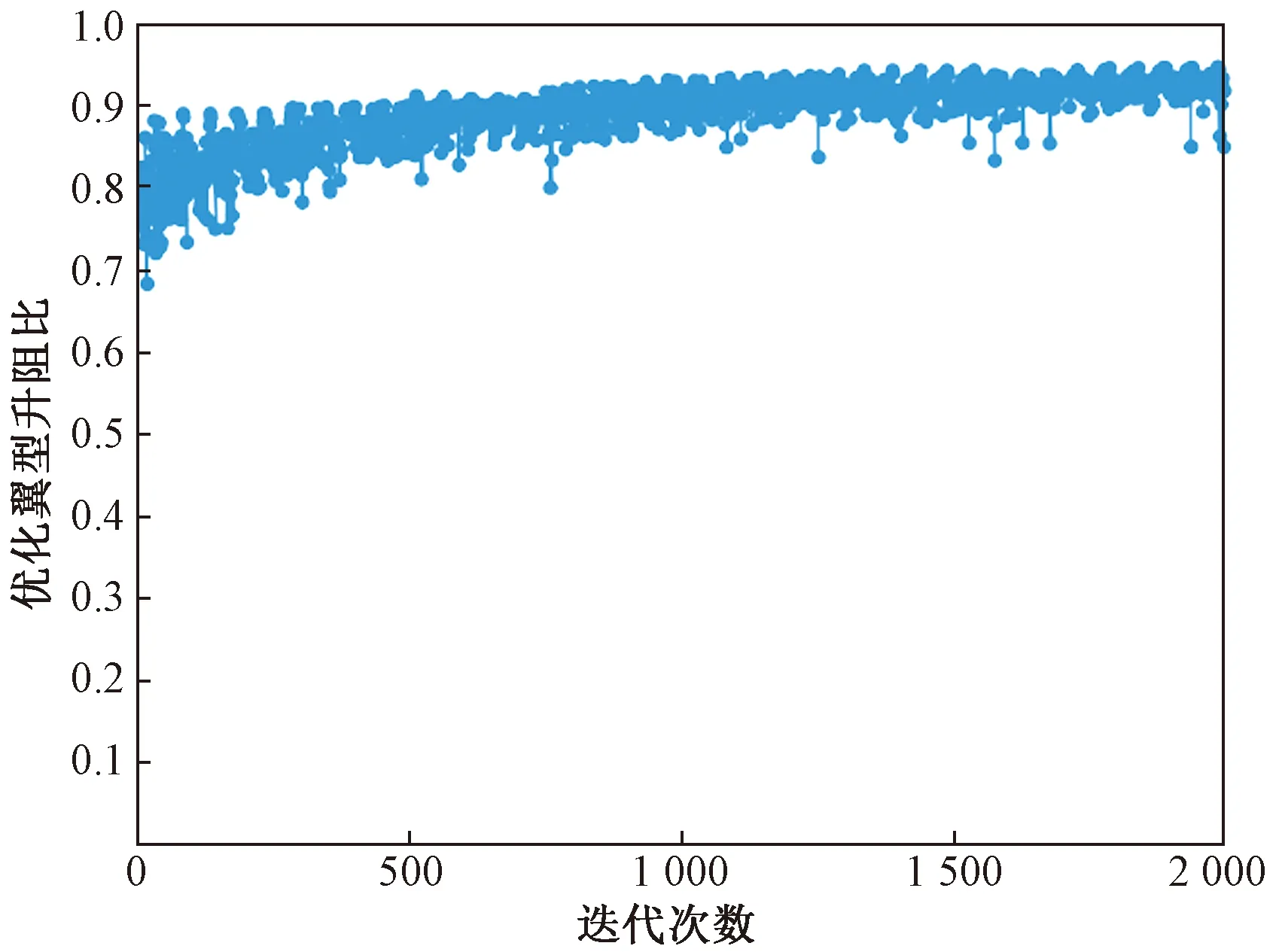
图4 翼型优化迭代过程Fig.4 Airfoil optimization iterative process

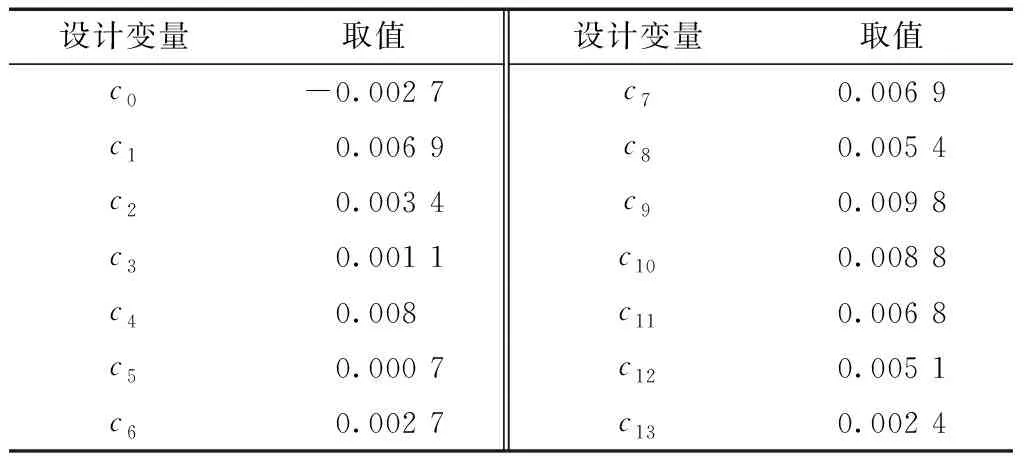
表3 优化翼型设计变量取值Table 3 Values of optimized airfoil design variables

设计变量取值对应的翼型轮廓即为优化翼型，在本文中命名为“优化翼型”。翼型优化前后轮廓曲线对比如图5所示，翼型轮廓的弦线位置用(x，y)表示，c为弦长，图中横坐标为翼型轮廓弦线横坐标值与弦长的比值，纵坐标为翼型轮廓弦线纵坐标与弦长的比值。从图5中可以看出，优化翼型的中弧线轮廓曲线已经是非对称图形，中弧线不再与弦长重合，优化翼型有明显的弯度变化。图6中，将翼型与风轮旋转轴直接连接的一侧定为翼型下翼面，另一侧则为翼型上翼面。相比初始翼型NACA0012，优化翼型的上翼面厚度增加，下翼面厚度减少，且下翼面厚度减少幅度大于上翼面的增加幅度。根据中弧线可以看出，靠近优化翼型前缘位置的下翼面厚度略大于上翼面厚度。

图5 翼型优化前后轮廓Fig.5 Airfoil optimized front and rear profile

如图6所示，初始翼型的相对厚度大于优化翼型，初始翼型的最大相对厚度为0.12c，其对应弦线上的位置0.30c；优化翼型的最大相对厚度为0.11c，其对应弦线的位置为0.264c。与初始翼型相比，优化翼型的最大相对厚度降低了0.01c，其对应弦线的位置向翼型前缘方向移动了12%；优化翼型的前缘部分与初始翼型基本一致，但后缘的夹角明显减小了。比较而言，采用自适应模拟退火算法对NACA4418 翼型优化后，翼型厚度变化在5%以内，最大厚度位于整个弦长的 0.24～0.35位置处[11]，基于CFD技术与遗传算法对DU97-W-300翼型优化后，相对厚度变化为1%，最大厚度的弦向位置由0.3c前移至0.294c。本文算法与这两种算法比较，最大厚度对应弦长位置均前移，其范围基本一致，但本文算法对于翼型厚度的优化更加明显，针对NACA0012的翼型厚度变化达10%左右。

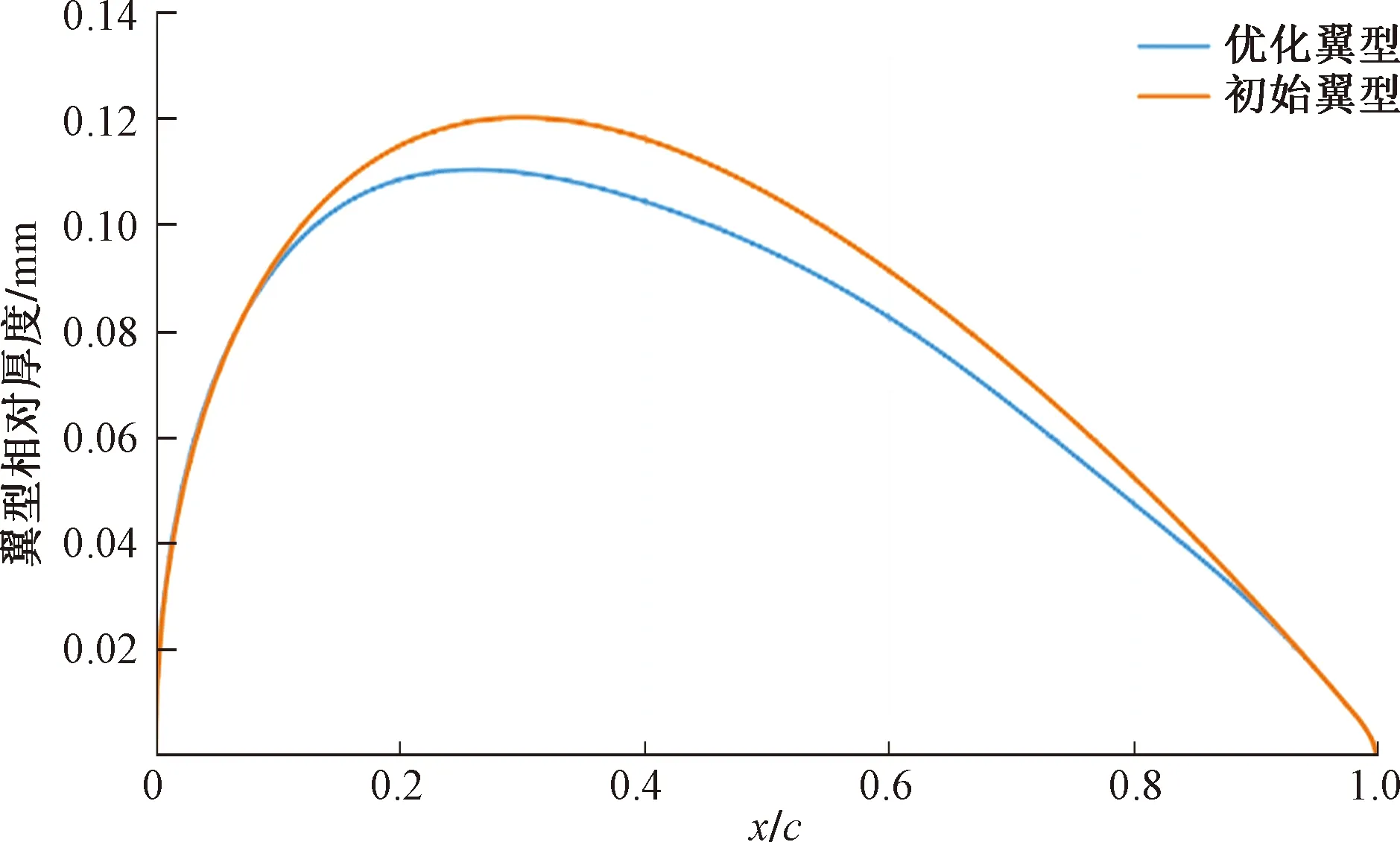
图6 翼型优化前后的相对厚度分布Fig.6 Relative thickness distribution before and after airfoil optimization

3.2 翼型气动参数

优化目标为翼型的最大升阻比，并对升、阻力系数设置了约束条件，根据优化结果，优化翼型与初始翼型的气动数据如表4所示。

表4 翼型优化前后的气动数据Table 4 Aerodynamic data before and after airfoil optimization

与初始翼型相比，8°攻角下优化翼型的升阻比和升力系数都得到了明显提高，升阻比提高了17.78%，升力系数提高了16.7%。由于在优化过程中对阻力系数进行了约束，因此阻力系数的变化可以忽略不计。比较而言，采用标准模拟退火算法对NACA4418 翼型优化后，翼型阻力系数减小10.6%，升力系数提高1.45%，升阻比提高13.48%[11]，而本文算法通过抑制阻力系数，可获得更高的升力系数和升阻比。

图7、图8分别给出了初始翼型和优化翼型的压力和速度云图。从优化前后的压力云图来看，相比初始翼型，优化翼型的上翼面压力增加，下翼面减少了，但上翼面的压力分布更加均匀，并且尾缘位置的涡流现象降低了；从速度云图来看，上翼面速度增加下翼面速度降低，尾缘附近速度有所增加。翼型的压力与速度在优化前后的变化可能是翼型的弯度增加导致的，翼型的弯度增加，气体在前缘的流动变大，吸力增大；翼型最大厚度对应在弦长位置上向前移动，前缘和尾缘处的气流变细，从而导致气体的流速加快，压力变小，升力系数变大。在优化中对阻力系数设置了约束条件，阻力系数几乎不发生变化，因此升阻比增大。

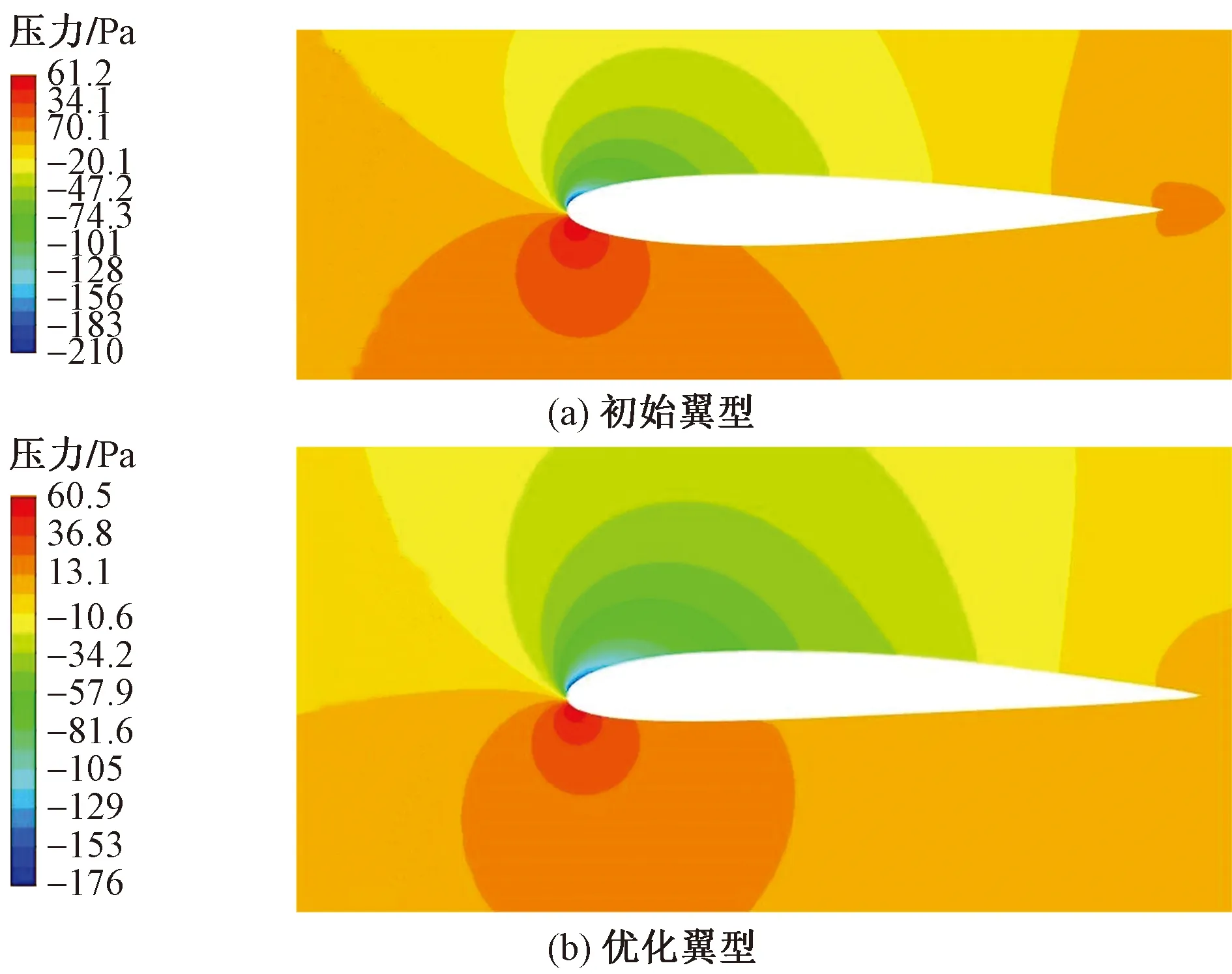
图7 翼型优化前后压力云图Fig.7 Pressure cloud diagram before and after airfoil optimization

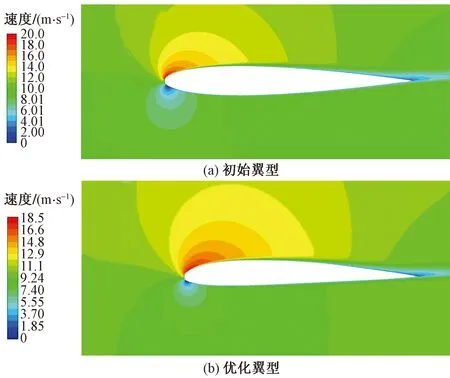
图8 翼型优化前后速度云图Fig.8 Speed cloud diagram before and after airfoil optimization

另外分别计算了攻角为0°、6°、12°初始翼型与优化翼型的压力系数，计算结果如图9所示。当攻角为0°[图9(a)]时，已经可以明显看出两者的差异了，因为初始翼型属于对称翼型，上下翼面的压力分布对称，此时无升力。但优化翼型并非对称形状，因此上下翼面的压力存在压差，此时的优化翼型具有升力。当攻角为6°[图9(b)]时，初始翼型与优化翼型的最大正压力系数值均位于翼型的前缘处，值约为1，在弦长0.1c内，初始翼型上下翼面压力系数的绝对值大于优化翼型，但在0.1c到1c的范围内情况则相反。当攻角为12°[图9(c)]时，优化翼型最大负压力系数明显高于初始翼型，从图中可以看出初始翼型负压力系数的最下端为-4，优化翼型则为-2.6左右。

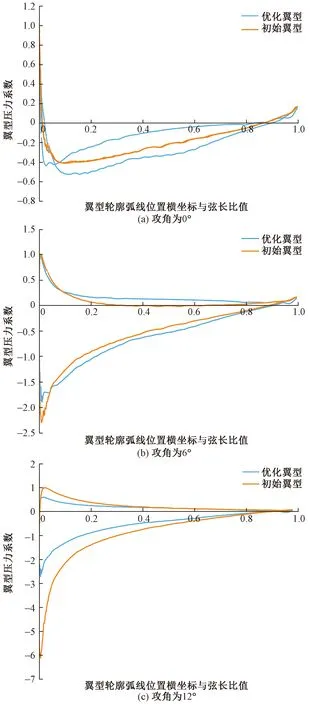
图9 攻角为0°、6°、12°下的压力系数变化情况Fig.9 Pressure coefficient changes at angles of attack of 0°, 6° and 12°

4 结论

首先对多岛遗传算法原理作了基本阐述，构建了翼型优化数学模型，建立基于多岛遗传算法与CFD耦合的垂直轴风力机翼型优化程序。该程序主要依靠多岛遗传算法顺序调用翼型参数化程序、ICEM网格划分、Fluent流场计算，并对流场计算结果进行处理。以NACA0012翼型作为初始研究对象，使用该算法进行优化算例分析，主要分析结论具体如下。

(1)相比初始翼型，优化翼型已经是非对称翼型，其最大相对厚度降低了1%，为0.11c；其最大相对厚度对应在弦上的位置向翼型的前缘移动了0.036c。并且优化翼型的中弧线不再与弦线重合，翼型弯度明显增加，中弧线偏移量最大值为0.017 4c。优化翼型的前缘半径变化不大，但翼型尾缘夹角明显变小，翼型上翼面轮廓线相对平缓。

(2)优化翼型的升阻比、升力系数均有提高，升阻比提高了17.78%，升力系数提高了16.7%。

(3)分析了攻角0°、6°、12°时翼型优化前后的上下翼面压力系数变化情况。发现当攻角为0°时，优化翼型相比对称翼型已有升力，到攻角为12°时，优化翼型的负压力系数明显高于初始翼型。