石炭系浅层低压砂岩油藏压裂方式优选
2023-02-11陈宏飞曹旭升冯海蛟彭越巨世昌李斯琪陈文顺胥新刚邓青玉
陈宏飞, 曹旭升, 冯海蛟, 彭越*, 巨世昌, 李斯琪, 陈文顺, 胥新刚, 邓青玉
(1.中国石油新疆油田分公司重油开发公司, 克拉玛依 834000; 2.中国地质大学(北京)能源学院, 北京 100083;3.北京中地金石科技有限公司, 北京 100085)
水平井和水力压裂技术的使用,能够改变流体在储层中的渗流方式,降低油气在储层中的渗流阻力[1-2],从而提高油气井产量和最终采收率。根据裂缝分布特点可将压裂模式分为两类,即常规压裂和体积压裂。常规压裂以经典线弹性断裂理论为基础,以一条主裂缝或多条互不相交的主裂缝来改变流体的流动方式,裂缝只与井筒发生流量交换,裂缝间无流量交换。体积压裂在形成一条或者多条主裂缝的同时,主裂缝与天然裂缝沟通,并且在主裂缝的侧向产生次生裂缝,实现对储层的全面改造[3-4]。体积压裂假设除了裂缝与井筒间的流量交换,裂缝之间也会发生流量交换。
国内外关于常规多段压裂水平井的理论研究始于20世纪90年代。1991年,Larsen等[5]给出了三维无限大储层多条有限导流裂缝压裂水平井不稳态渗流解析解,较好地呈现了早、中期渗流特征。1994年,Larsen等[6]给出了圆形和矩形有限导流垂直裂缝的压裂水平井的渗流模型,并给出解析解和相应试井图版。Guo等[7]利用格林函数研究无限导流多段压裂水平井渗流模型,获得了井底压力动态特征及各条裂缝间的流量分布规律,但未考虑缝间干扰。随后,Horne等[8]改进了Guo等[7]的模型未对缝间干扰考虑的不足,但未考虑裂缝导流的影响。1996年,基于Ozkan和Raghavan的点源解及Cinco-Ley和Samaniego有限导流裂缝的计算方法,Chen等[9]应用叠加原理给出了矩形封闭油藏多段压裂水平井有限导流裂缝在Laplace域的经典渗流模型。此后,大量学者基于Chen等[9]的方法扩展了水平井渗流模型,分析了二维和三维裂缝[10]、垂直与斜裂缝[11-13]、常规与非常规储层[14-15]下油气井产能及压力动态分布规律。
对于体积压裂,Warpinski[16]在1993年通过分析矿场资料,认为压裂可形成多条裂缝组成的复杂缝网改造区域。2004年和2005年,Fisher等[17-18]利用地震监测证明了体积压裂复杂网状裂缝的存在。2006年,Mayerhofe等[19]首次提出了页岩储层压裂改造区域的概念。对于体积压裂复杂缝网表征,国内外学者分别提出了分区、离散裂缝和双重介质等效的方法。分区表征方法将储层分为压裂破碎区和压裂支撑填充区[20-21],或将储层分为水力裂缝形成区、裂缝受效区、未改造区和边界控制区等[22]。离散裂缝模型分为嵌入式和非结构化离散裂缝模型[23-25]。前者对基质进行结构网格化,再将裂缝嵌入基质网格。后者采用非结构化网格划分储层,使其与裂缝网络相匹配,然后对裂缝进行降维处理。双重介质模型将压裂改造区假定为双重介质[26]。对于体积压裂数学模型求解,由于解析方法有较多的简化条件,较难描述体积压裂改造后复杂缝网的渗流特征[27-28],主要采用半解析方法和数值方法进行求解[29-32]。
上述回顾了不同压裂方式理论研究背景及发展历程,在实际工程中,常常会面对压裂方式的优选及裂缝参数优化等问题。目前,国内外裂缝参数优化方法主要有两种,分别是基于支撑剂数的解析方法[33-34]和结合一定经济参数评价的数值模拟方法。支撑剂指数法可以考虑砂体展布与储层裂缝的匹配关系,与实际工程更稳吻合。传统的数值模拟方法可考虑储层的非均质性等一些地质参数和流体性质,模型虽然可考虑复杂的流动机理,但是由于其对裂缝的等效处理,并没有使用支撑剂量的约束。现结合支撑剂数方法和数值模拟方法的优点,以泵入地层中的支撑剂量为约束条件,对体积压裂进行模型简化[35-39],建立数值模型。针对新疆油田J20区块埋深浅、压力低、储层中-低渗等典型地质特征,系统对比不同裂缝组合下的油井20年生产特征,评价油井生产潜力。揭示不同压裂方式下油井生产规律,为压裂方式的优选及裂缝参数的优化提供参考。
1 地质背景与方案设计
1.1 油藏概况
新疆油田J230井区石炭系油藏位于准噶尔盆地西北缘大型推覆构造-克乌断裂带前缘断块上,整体构造形态为北西高、东南低的单斜,局部存在鼻状构造。区块含油面积29.8 km2,石油地质储量2 978.67×104t,油藏中部深度620 m,原始地层压力8.6 MPa,饱和压力6.9 MPa。储层孔隙度4.5%~22.9%,平均7.26%;渗透率0.01~96.1 mD,平均1.14 mD。总体上,油藏类型为浅层低压砂岩油藏。目前,该区投产总井数309口(其中普通多段压裂水平实验井17口,体积压裂水平实验井10口),累计产油232.21×104t,采出程度7.8%。从目前生产情况看,体积压裂水平井初期产量高于普通多段压裂水平井,普通压裂水平井初期产量高于普通直井。但是体积压裂投资规模更大,风险高。因此,需要评价体积压裂和普通多段压裂下的油井长期生产潜力,为经济可行性评价提供参考。
1.2 模型建立与方案设计
区块目前投产水平井水平段长度585~1 467 m,平均950 m;裂缝条数5~29条,平均18条;裂缝段间距34~106 m,平均53 m,以40 m间距为主;水平井单井加砂量307~1 290 m3,平均765 m3。如图1所示,为了简化模型,选取一个典型的裂缝单元(3段水平井)开展数值模拟研究。模型基本假设如下。
(1)水平井位于矩形油藏中央,裂缝为理想规则的垂直裂缝。
(2)如图1(a)所示,普通多段压裂水平井中的“段”定义为一条垂直于水平井(粗蓝线)方向的主裂缝(粗红线),表示两条主裂缝之间的距离定义为“段间距”。
(3)如图1(b)所示,体积压裂中“段”定义为垂直于水平井的主裂缝(粗红线)和平行于水平井的次裂缝(细黑线)构成的一个裂缝网络,段内的主裂缝定义为“簇”,簇与簇之间的距离定义为“簇间距”,平行于水平井的次裂缝长度定义为“带宽”;定义两个裂缝网络中心线之间的距离为“段间距”。

图1 普通多段压裂与体积压裂裂缝分布示意图Fig.1 Schematic diagrams of conventional multi-stage fracturing and volume fracturing
(4)根据区块实际体积压裂情况将体积压裂简化为3段6簇和3段15簇模型,模型如图1(b)和图1(c)所示。其中3段6簇模型为压裂3段,每段2簇裂缝,共有6条垂直于水平井的主裂缝,12条平行于水平段的次生裂缝。3段15簇模型为压裂3段,每段5簇裂缝,共有15条垂直于水平井的主裂缝,12条平行于水平段的次生裂缝。
考虑生产中地层压力会低于饱和压力,选择油、气、水三相黑油模型进行模拟。考虑模型收敛性影响,采用局部网格加密及等效裂缝导流能力处理裂缝,设定主裂缝宽度为次裂缝两倍,主裂缝等效渗透率为1 000 mD,次裂缝等效渗透率为100 mD[39]。油井生产制度为定井底流压2 MPa,模拟生产时间20年。模型其他参数如表1所示。

表1 模型参数表Table 1 Parameters of the basic simulation model
该区储层渗透率K为0.01~96.1 mD,选取3个典型值0.01、1和100 mD进行模拟。结合区块水平井实际压裂参数,设计4组共24个模拟方案。其中,第一组方案(方案1~方案6)模拟不同渗透率下普通多段压裂水平井裂缝半长Xf对生产的影响。第二~第四组方案(方案7~方案24)模拟不同渗透率下体积压裂水平井不同裂缝参数组合对生产的影响。
以方案1、方案3和方案5作为3个渗透率对应的基础方案,并采用相同的支撑剂用量。为了更好地对比体积压裂与普通多段压裂,方案7~方案24采用基础方案的支撑剂用量。在支撑剂用量固定的情况下,可以通过图1及表1确定裂缝相关参数,具体方案参数如表2所示。
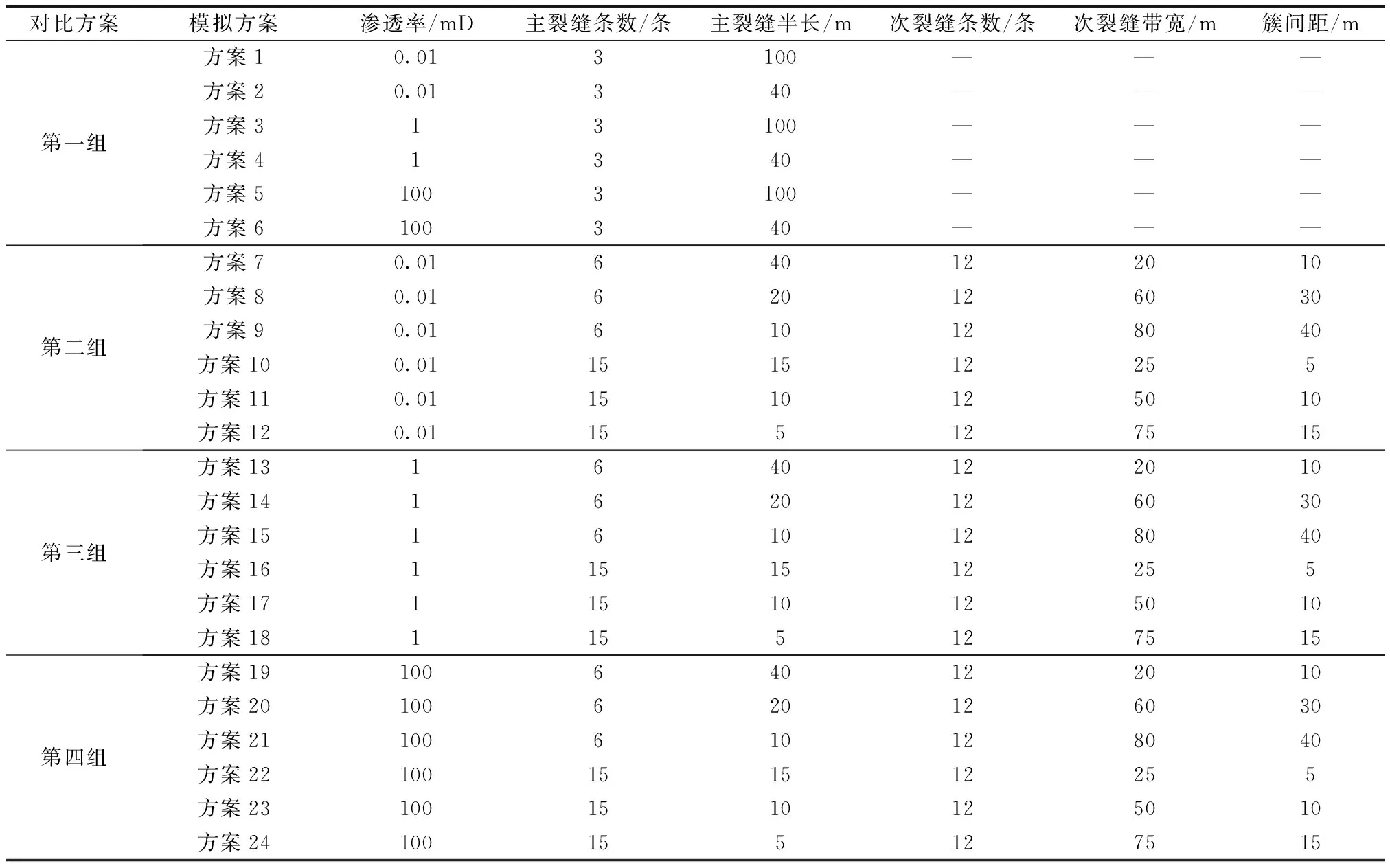
表2 压裂模拟方案表Table 2 Parameters of numerical simulation scheme
2 石炭系浅层低压砂岩油藏压裂方式优选
2.1 普通多段压裂生产特征分析
根据方案1~方案6的参数模拟不同储层渗透率下,裂缝长度对生产的影响。如图2所示,以单段产量和单段累计产量作为对比,便于通过倍乘裂缝段数估算真实多段压裂水平井产量。从图2可以看出,在相同的渗透率下,裂缝越长,单段初期产量越高,累计产油量越多,如渗透率为1 mD,裂缝半长为40 m和100 m时,单段初期产量分别为1.6 m3/d和1.71 m3/d,20年平均单段裂缝累计产量分别为1 006 m3和1 233 m3。如图3所示为方案1~方案6在模拟期末(第20年)的压力场分布,压力值越大,表明储量动用程度越小。可以看出,地层渗透率低时,如渗透率为0.01 mD,裂缝半长越长,压力波及范围越广,储量动用程度越高。随地层渗透率的增大,裂缝半长对储量动用程度影响减弱,如地层渗透率为100 mD,裂缝长度对储量动用的影响无明显差别。
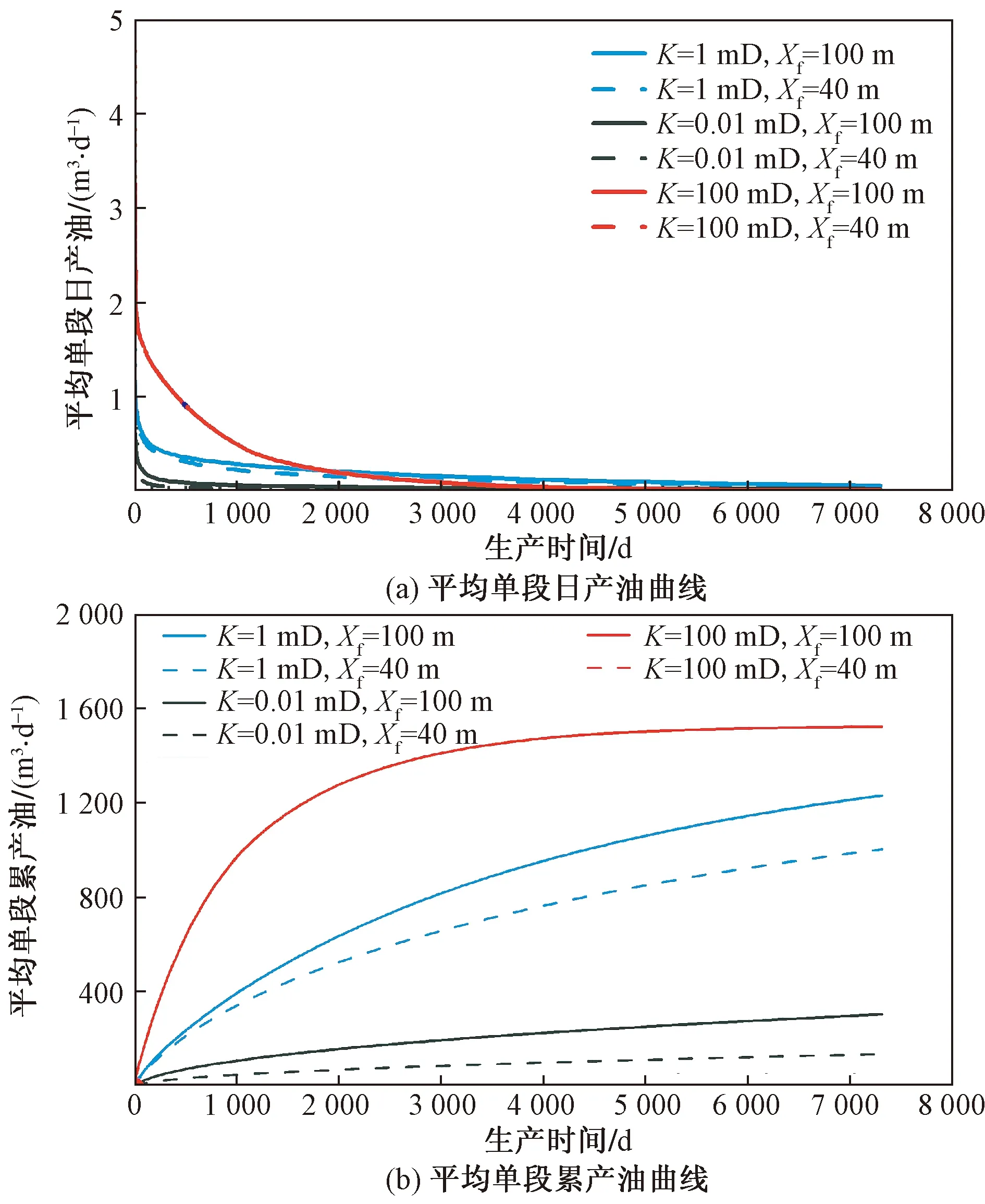
图2 普通多段压裂不同渗透率不同裂缝半长平均单段日产油和累产油曲线Fig.2 Average single-stage oil-flow rate and cumulative production for varying permeabilities and fracture half lengths
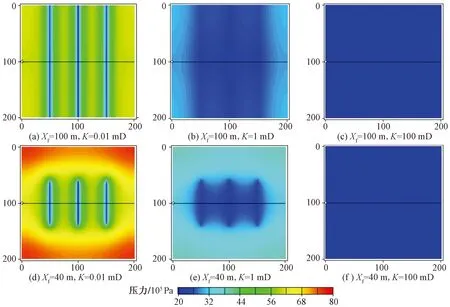
图3 不同渗透率下普通压裂3段3簇生产20年地层压力场图Fig.3 Pressure distribution after 20 years for different permeabilities in conventional fracturing of 3 stages 3 clusters
表3所示为方案1~方案6对应的初期半年平均日产和20年采出程度。可以看出,储层物性越好,相同裂缝长度下,初期半年平均日产和20年采出程度越大;储层渗透越低,增大裂缝长度对短期产量与长期累产均有明显的增幅,如渗透率为0.01 mD,裂缝半长100 m相对于半长40 m,初期半年平均日产增加1.89倍,20年采出程度增加2.21倍;但这种增幅随地层渗透率增大而逐渐减小,如地层渗透率为1 mD时分别对应1.09倍和1.23倍,100 mD时短裂缝与长裂缝生产效果一致。

表3 不同渗透率不同裂缝半长采收率统计表Table 3 Statistic results of recovery for different permeabilities and different fracture half length
通过图2、图3和表3的对比可以看出:当采用普通多段压裂开发油藏时,低渗透储层应尽量增大裂缝长度,高渗透率储层可适当减小裂缝长度,以提高经济效益。
2.2 体积压裂与普通多段压裂对比分析
以方案1、方案3和方案5对应的不同渗透率普通多段压裂模型为基础方案(3段3簇),对比相同支撑剂用量下的3段6簇体积压裂[图1(b)]开发效果(方案8,方案14和方案20)。
图4展示了不同渗透率不同压裂方式下平均单段日产油和累产油曲线。可以看出:渗透率越高,气井初期产量越高;相比于普通多段压裂,体积压裂在不同渗透率下初期产量高于普通多段压裂,但产量递减速度也更快[图4(a)];从累产曲线来看[图4(b)],极低渗透率时(0.01 mD),体积压裂开发效果始终优于普通多段压裂,普通多段压裂单段累产油308 m3,体积压裂3段6簇单段累产油326 m3,比普通多段压裂增加6%;渗透率为1 mD时,早期体积压裂占优,后期普通多段压裂累计产量更大;渗透率为100 mD时,体积压裂与普通多段压裂开发效果接近,20年累计产量差别在2%以内。

图4 普通压裂3段3簇与体积压裂3段6簇平均单段日产油和累产油曲线Fig.4 Average single-stage oil-flow rate and cumulative production in conventional fracturing of 3 stages 3 clusters and volume fracturing of 3 stages 6 clusters
由此可见,极低渗透率时(0.01 mD),由于体积压裂近井储层改造程度高,初期累计产量高,生产效果好。当渗透率为1 mD时,由于渗透率提高,基质渗流能力提高,普通多段压裂沟通储层面积大,长缝所穿过储层都有产量贡献,普通多段压裂模式表现出更大的生产潜力,累计产量会超过体积压裂,长期来看生产效果较好。当渗透率为100 mD时,体积压裂主要影响前期开发效果,长期来看,体积压裂与普通压裂累计产量差别不大,开发效果接近。
图5展示了不同压裂方式生产20年压力场图,由图5可知,体积压裂与普通多段压裂储量动用范围不同,剩余储量分布有差异,具体表现为:极低渗透率时(0.01 mD),普通多段压裂储量动用程度较均匀,但整体储量动用程度低,体积压裂近井裂缝网络改造区域压力降落大,储量动用程度高,体积压裂开发效果优于普通多段压裂;当渗透率为1 mD时,储层基质渗流能力提高,普通多段压裂储量动用程度提高,且模型边部储量都能得到动用,而体积压裂边部裂缝未改造区剩余较多未动用储量,普通多段压裂储层改造范围大的优势得以体现,开发效果优于体积压裂;渗透率为100 mD时,由于储层基质渗流能力较好,模型整体储量都能得到较好动用,不同压裂模式下压力场图分布接近。
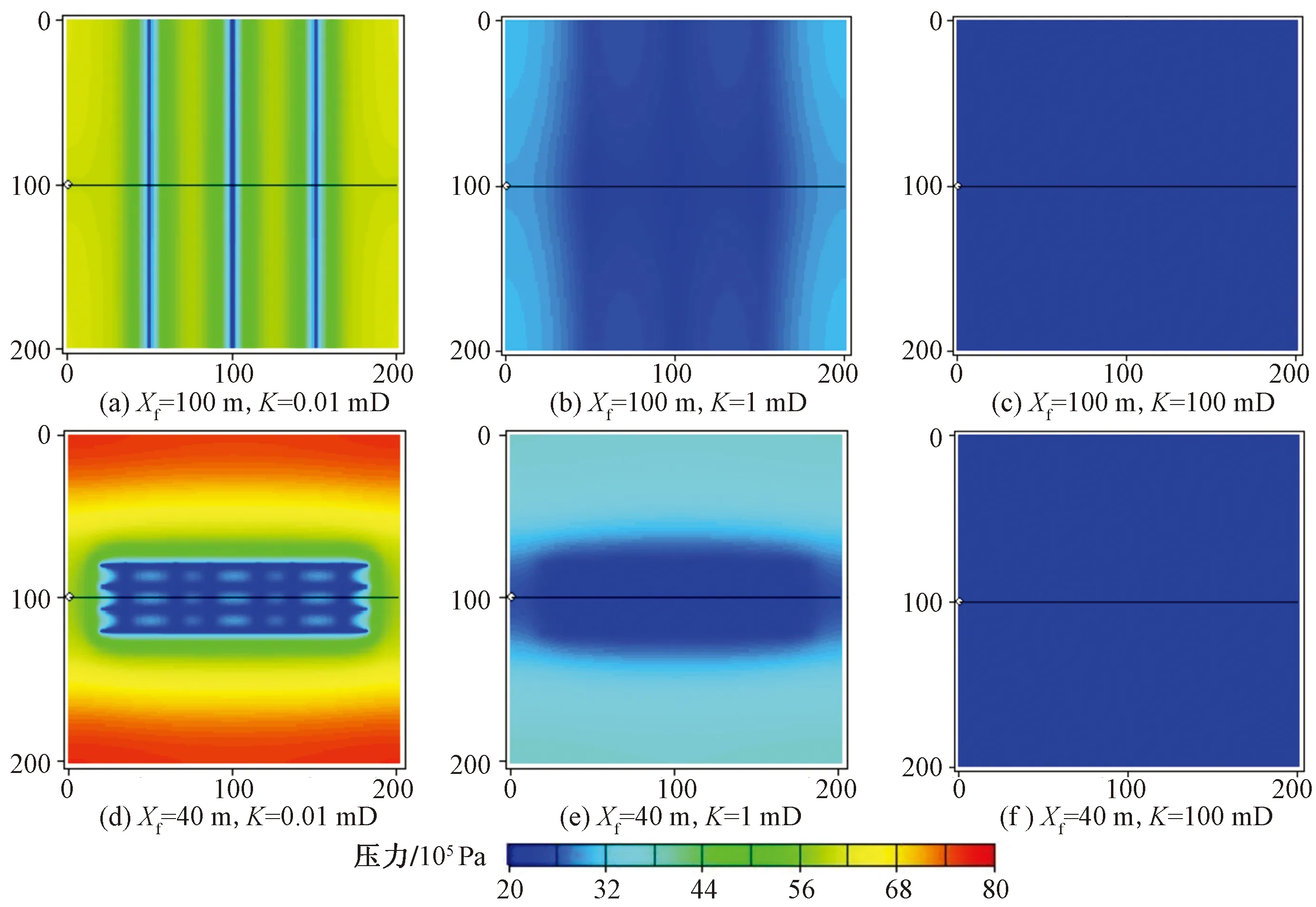
图5 普通压裂3段3簇与体积压裂3段6簇生产20年地层压力场图Fig.5 Pressure distribution after 20 years in conventional fracturing of 3 stages 3 clusters and volume fracturing of 3 stages 6 clusters
2.3 不同裂缝参数组合下的体积压裂效果分析
根据方案7~方案24的参数模拟相同支撑剂用量下,体积压裂不同裂缝参数组合对生产的影响。不同渗透率体积压裂不同裂缝簇数下平均单段累产油曲线如图6所示。可以看出:在渗透率较小情况下(0.01 mD和1 mD),体积压裂3段6簇累计产量高于3段15簇;随着储层渗透率的提高,体积压裂裂缝簇数对生产影响减弱,如渗透率为100 mD时,体积压裂3段6簇和3段15簇累计产量产别不大,生产效果接近;不同储层渗透率条件下,体积压裂存在最优裂缝簇数;极低渗透率储层(K=0.01 mD),3段6簇半长20 m裂缝在近井区对储层有较好的改造程度,且有效改造面积大,开发效果最优,这也是决定区块长期生产的主控因素;随着储层渗透率提高,流体在储层基质中渗流能力提高,在一定压差下可参与流动,未被裂缝沟通区域储量也能得到一定程度动用,因此沟通面积更大的缝网生产效果好,较低渗透率储层(K=1 mD),3段6簇半长40 m裂缝在横向和纵向上沟通面积大,开发效果最优;渗透率较高时(K=100 mD),体积压裂3段15簇在前期有优势,长期生产来看,3段6簇和3段15簇开发效果接近。
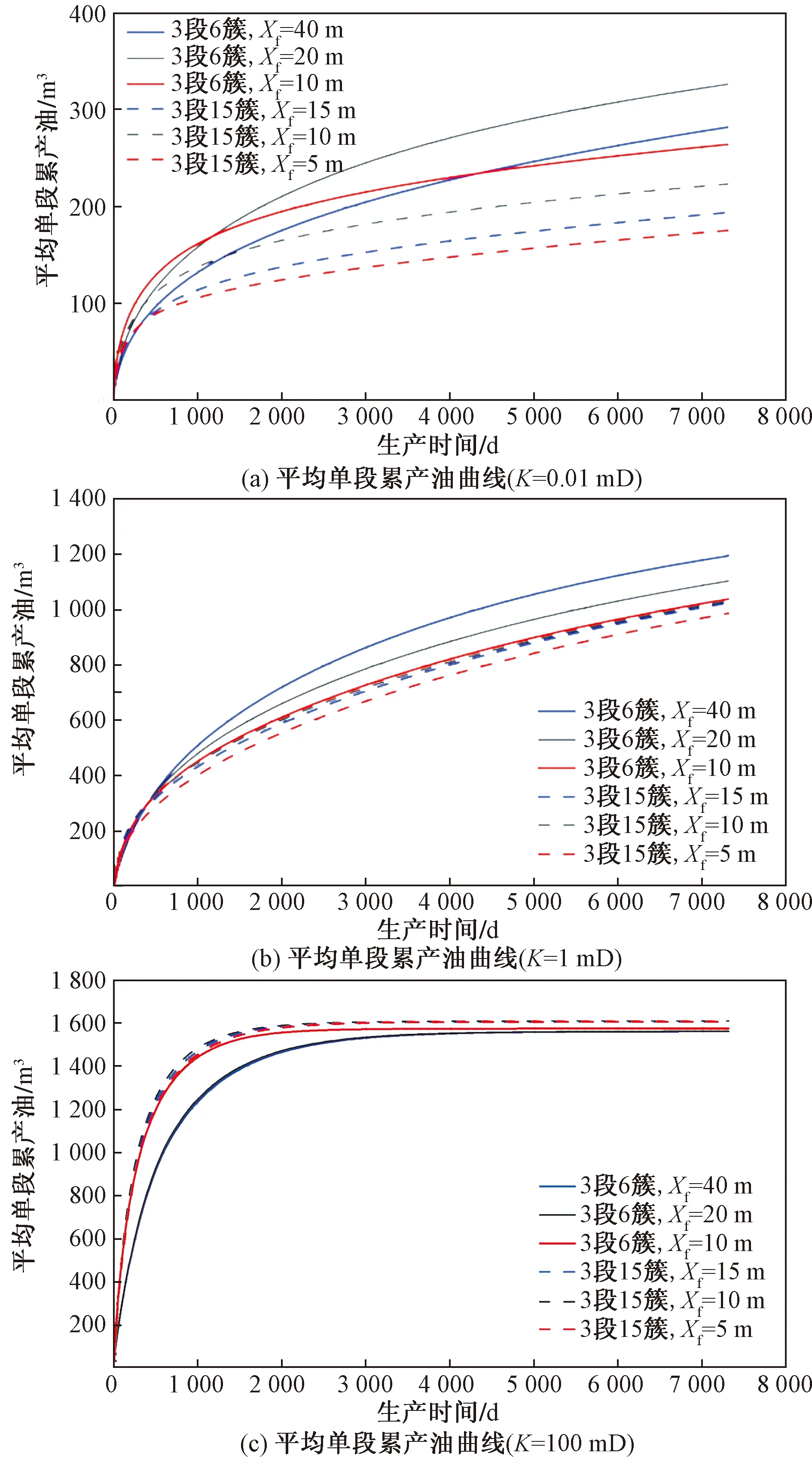
图6 不同裂缝簇数下体积压裂平均单缝累产油曲线Fig.6 Average single-stage cumulative oil production for varying number of fracture clusters in volume fracturing
图7展示了体积压裂不同裂缝簇数下压力场图。
由图7可知:储层渗透率越高,压力波及范围越广,储量动用面积越大;体积压裂相同的裂缝簇数下,主裂缝长度越长,次裂缝带宽越小,纵向裂缝能够沟通的储层面积越大,生产效果越好;在较短的主裂缝下,水平井水平段储层改造效果好,近井区储量都得到了动用,但在较低的储层物性下,边部剩余未动用储量较多;对比3段6簇体积压裂模式,3段15簇裂缝簇数更多,纵向上,压力波及的范围更小,剩余油未动用区面积更大。

K=0.01 mD时,色标刻度范围为(20~80)×105 Pa;K=1 mD和K=100 mD时,色标刻度范围均为(20~40)×105 Pa;各列共用一个色标刻度轴,置于各列下方图7 不同裂缝簇数下体积压裂压力场图Fig.7 Pressure distribution for varying number of fracture clusters in volume fracturing
通过对比可知,缝网对储层的有效改造能力是决定油井长期生产的主控因素。有效改造能力包括两个方面,一是对储层近井附近的改造面积。由于设定每种改造模式支撑剂用量相等,体积压裂裂缝簇数越多,缝网的布局模式越集中,对近井附近储层改造程度越高。二是改造对储层的长期影响范围,即储量有效动用范围。裂缝簇数越多,裂缝越集中,改造体积越小,长期生产来看,效果可能变差,如3段15簇下,渗透率为100 mD的储层依然存在大量的剩余油未动用。由此可见,要获得较大的初产和累产,储层渗透率、裂缝改造规模存在最优的匹配关系。
2.4 石炭系浅层低压砂岩油藏压裂方式优选
通过前面的模拟,汇总常规多段压裂与体积压裂各个方案20年采出程度,如表4所示。在相同的支撑剂用量下,普通多段压裂储层连通范围更大,而体积压裂对于近井附近的储层有效改造程度更高。体积压裂相对于普通多段压裂具有更高的初产优势,不同地层渗透率存在最佳压裂开发策略。当储层渗透率为0.01 mD时,最优压裂方式为体积压裂3段6簇裂缝,裂缝半长20 m,20年采收程度4.73%;当储层渗透率为1 mD时,最优压裂方式为普通压裂3段长裂缝,20年采收程度17.88%。当储层渗透率为100 mD时,体积压裂与普通压裂效果基本相同,采出程度接近。
J230区渗透率0.01~96.1 mD,平均1.14 mD,为追求长远的生产效益,建议以普通多段压裂为主。在局部极低渗透率区域,可以适当采用体积压裂方式,弥补地层渗流能力的不足,从而提高采收率。

表4 不同压裂模式不同渗透率采出程度表Table 4 Recovery degrees for different fracturing methods and different permeabilities
3 结论与建议
利用数值模拟技术,采用支撑剂用量为约束条件,以J230井区石炭系浅层低渗-致密砂岩油藏为地质背景建立模型,对比了不同储层物性不同压裂方式下生产规律,明确了普通多段压裂和体积压裂的适应性,主要结论和认识如下。
(1)对于普通多段压裂,裂缝半长越长,储层改造面积越大,储量动用程度越高,累计产量越多,气井生产效果越好。但随着储层渗透率的增加,裂缝长度对生产效果的影响逐渐减弱。
(2)对比普通多段压裂与体积压裂生产效果,普通多段压裂优势在于裂缝具有更大的穿透比。在储层具有一定的渗流能力前提下,多段压裂水平井长期生产效果较好。而体积压裂模式对近井附近储层改造程度相对较好,在较低的渗透率下和生产前期有明显的优势。
(3)缝网对储层的有效改造能力是决定油井长期生产的主控因素。有效改造能力包括两部分,对储层近井附近的改造面积和改造对储层的长期影响范围。要获得较大的初产和累产,储层渗透率、裂缝改造规模存在最优的匹配关系。渗透率低,体积压裂效果好,渗透率高(K>1 mD),常规长缝压裂效果好。
(4)J230区渗透率分布在0.01~96.1 mD,平均1.14 mD。为提高长远的生产效益,根据模拟结果,建议以普通多段压裂为主,在局部极低渗透率区域,可以适当采用体积压裂方式,以提高采收率。
