考虑VSC-HVDC作用的LCC-HVDC系统短路比实用计算

杨晓雷，韩中杰，叶 琳，江俊贤，王奕鑫，王冠中

（1.国网浙江省电力有限公司嘉兴供电公司，浙江 嘉兴 314000；2.国网浙江省电力有限公司，杭州 310007；3.浙江大学 工程师学院，杭州 310027；4.浙江大学 电气工程学院，杭州 310027）

0 引言

LCC-HVDC（电网换相换流器型高压直流输电）与VSC-HVDC（电压源换流器型高压直流输电）馈入同一受端电网［1-3］。所形成的混合直流馈入系统已成为我国新型电力系统的代表模式之一［4-5］。交直流系统的相互作用［6］深刻影响受端电网的安全稳定运行，因此准确量化电网强度［7-8］，反映交直流相互作用程度，对于电网规划和运行是非常重要的。

文献［9］通过三阶雅克比矩阵的奇异性分析LCC-HVDC单馈入系统功传输极限与电网强度的关系。文献［10］基于模态解耦，利用特征值解耦的思路提出广义短路比的指标，以此表征LCCHVDC 多馈入系统的电网强度。文献［11］基于阻抗等值，将LCC-HVDC、VSC-HVDC 混合双馈入系统等效成LCC-HVDC 单馈入系统，提出了HEESCR（混合馈入等效有效短路比）。文献［12］考虑了VSC-HVDC对LCC-HVDC等值临界阻抗的影响，类比LCC-HVDC 单馈入ESCR（有效短路比）指标，提出了EESCR（等值有效短路比）指标。综合上述研究，文献［9-10］仅研究了LCCHVDC 多馈入系统的电网强度作用机理；在混合直流馈入系统的电网强度与传输极限方面，文献［11-12］均通过将VSC 进行阻抗等值，在此基础上修正传统LCC-HVDC 单馈入系统的电网强度指标，缺乏关于指标作用机理以及指标临界值性质方面的深入分析［13］，导致难以形成混合直流馈入系统中电网强度的物理认识。

针对上述问题，本文首先根据交直流系统准稳态模型建立了LCC-HVDC和VSC-HVDC混合直流馈入系统的交流侧与直流侧的雅克比矩阵。其次，结合矩阵变换，通过降阶雅克比矩阵奇异表征LCC-HVDC 功率传输极限，得到系统位于临界稳定时的判断条件；进一步类比传统直流单馈入系统电网强度判据，得到适用于评估混合直流馈入中LCC-HVDC 系统静态电压稳定性的短路比指标及其临界值，并说明在VSC-HVDC 的实际运行范围内，系统的稳定裕度与VSC 运行方式存在明确的显函数关系，因此能够通过短路比指标有效评估系统的电压稳定裕度。最后，通过PSCAD/EMTDC及MATLAB仿真算例验证了所提分析方法的可行性和有效性。

1 混合直流馈入系统准稳态模型

图1 为LCC-HVDC 和VSC-HVDC 双馈入系统的拓扑结构，其中，Pd1和Pd2分别表示LCCHVDC 及VSC-HVDC输送的有功功率；Qd1和Qd2分别为两回直流注入交流电网的无功功率；Id1和Id2分别表示LCC-HVDC 及VSC-HVDC 输送的电流；P1、P2、Q1、Q2分别表示交流网络馈入的有功和无功功率；b10和b20表示交流系统的戴维南等值导纳，b12为换流站间联络线导纳；U1∠θ1和U2∠θ2分别表示换流站交流母线电压幅值和相角；Bc1表示无功补偿装置的等值导纳；E1和E2表示交流系统的等值内电势。

图1 LCC-HVDC、VSC-HVDC混合馈入系统Fig.1 Dual-infeed HVDC system of LCC-HVDC and VSCHVDC

以下用U0∠θ0统一表示无穷大电网电压（即忽略E1和E2之间的相角差）。系统潮流方程表示为：

式中：bij和θij分别表示节点i和j之间的等值电纳及电压相角差、方程式（1）—（4）表征系统的交直流系统耦合特性。

2 混合馈入系统雅可比矩阵

基于LCC-HVDC和VSC-HVDC端口特性以及交流网络的耦合，推导混合直流馈入系统的降阶雅克比矩阵以及相应的临界稳定条件。

2.1 LCC-HVDC单馈入系统的雅可比矩阵

首先建立LCC-HVDC系统在CP-CEA（定功率定熄弧角）和CC-CEA（定电流定熄弧角）两种控制方式下的降阶雅克比矩阵，并通过矩阵奇异条件分析功率传输极限。

CP-CEA/CC-CEA 控制方式下的LCCHVDC均通过增加直流电流来提高直流输送功率，该控制功能的实现基础为传输功率与电流存在正反馈关系。据此，文献［4］给出了系统功率传输极限的定义：当增加电流时，传输功率不增反降，即认为直流已达传输极限，此时直流功率失去可控性。

本文在LCC-HVDC准稳态方程组［8］基础上采用文献［9］中的标幺化方法建立标幺值模型。LCC-HVDC设备侧端口特性方程为：

式中：Ud1表示LCC-HVDC 直流电压；γ表示关断角；X表示换向电抗大小；φ表征功率因数角；k为直流侧电压基准值与交流测电压基准值的比值；K为变压器变比。

文献［14］提出以三阶雅克比矩阵奇异作为LCC-HVDC的传输极限判据，即以电流、功角和交流电压的微增量ΔId、Δθ和ΔU作为自变量，以直流传输功率、节点注入有功和无功功率的微增量ΔPd1、ΔP1和ΔQ1作为因变量建立的状态雅克比矩阵表征系统的功率传输特性［15］（对CP-CEA 而言，当研究对象为直流传输功率与电流的关系时，不能令ΔPd1=0）。考虑CP-CEA/CC-CEA 控制方式下，针对LCC-HVDC 馈入系统的功率稳定问题，所对应的三阶雅克比矩阵JPB如式（9）所示：

式中：JPdId等符号皆为下标对应的直流侧/交流测变量之间的偏导数。

由于JPdId≠0，式（9）中的三阶雅克比矩阵奇异性等价于降阶雅可比矩阵JLCC+JAC的奇异性：

其中，JLCC代表直流侧雅可比矩阵：

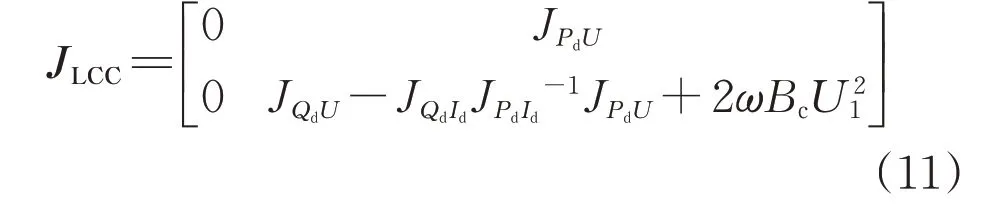
JAC表示交流雅可比矩阵，对应潮流方程线性化结果，具体表示为：

CP-CEA和CC-CEA两种控制方式均在矩阵JPB奇异的条件下到达直流传输极限［6，10］，对应的临界短路比约为2［15］。

2.2 VSC-HVDC直流侧雅可比矩阵

VSC-HVDC考虑不同控制方式的雅可比矩阵元素分别为：

1）定功率控制方式

考虑VSC-HVDC 定功率控制方式下，直流设备侧雅可比矩阵满足［18］：

2）定交流电压控制方式

考虑VSC-HVDC 定交流电压控制方式下，对应设备侧雅可比矩阵满足：

综合上述两种控制方式，VSC-HVDC直流侧雅可比矩阵可统一表示为：

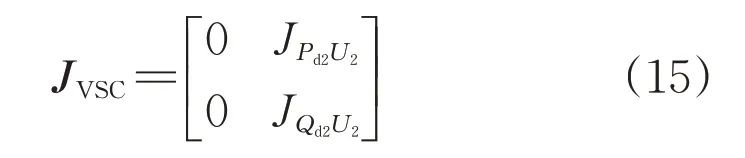
2.3 混合馈入系统的雅可比矩阵

根据前面两节的内容，可将混合馈入系统的雅克比矩阵简单表示如下：

3 混合直流馈入系统短路比计算方法

3.1 短路比指标的定义

根据图1所示拓扑，定义混合直流馈入系统中用于评估传输极限的SCR（短路比）指标表示为：

式中：det(B)表示导纳矩阵的行列式，det(B)/b22表征VSC-HVDC 接入后交流网络的修正等值导纳，物理上代表将VSC-HVDC 外部电路折算到LCC-HVDC单馈入系统中的结果。折算过程如图2 所示，根据工程中VSC-HVDC 容量较之LCCHVDC 要小很多，其对电网强度的影响也远小于LCC-HVDC，故在图2 中用虚线表示等效过程前的VSC-HVDC 并在电路折算中忽略其影响。值得说明的是，当忽略混合馈入系统中的VSCHVDC 以及与之相关的交流线路时，式（17）中的短路比指标化简为-b10/Pd1，等于LCC-HVDC单馈入系统SCR。

图2 SCR指标对应的外部电路过程示意图Fig.2 Schematic diagram of the external circuit process corresponding to the SCR indicator

所提指标的有效性可通过对2.3节中矩阵奇异所代表的临界稳定条件进行说明。

1）VSC-HVDC定功率控制方式

系统临界稳定时，对应式det(JDPB′)=0：

式中：bij表示节点i与节点j之间的互导纳。

观察式（18）可知，该临界稳定条件类似LCCHVDC单馈入系统的临界稳定条件［10］，即

结合式（19）可得考虑VSC-HVDC 定功率控制方式下，混合直流馈入系统对应的修正参数T′为：

进一步整理可得临界短路比CSCR为［10］：

2）VSC-HVDC定交流电压控制方式

临界稳定条件为式（22）所示，其对应式（16）删去JQd2U2元素所在行列并计算行列式的结果：

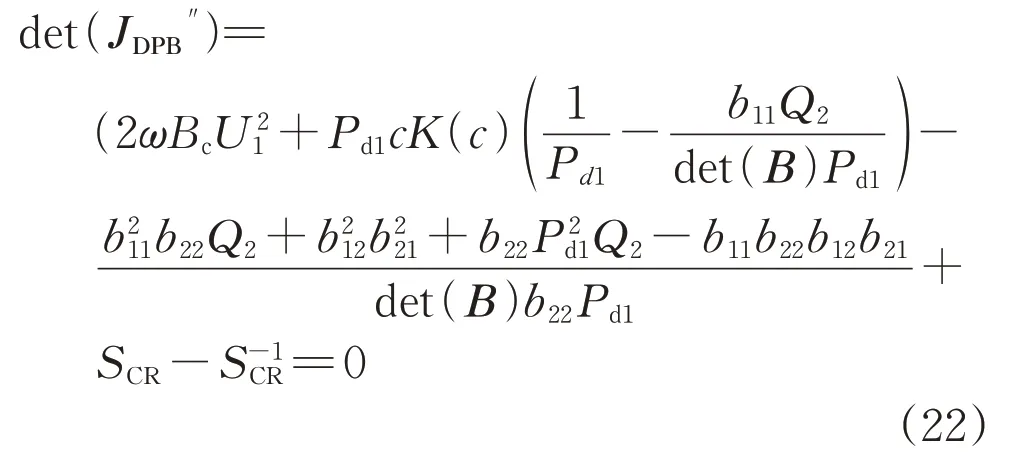
由式（22）可知，考虑VSC-HVDC 定电压控制方式下，混合直流馈入系统的修正参数T″为：

该控制方式下的CSCR 为把式（23）得到的修正参数代入式（21）的结果。

当混合直流馈入系统的SCR下降到CSCR时，系统额定运行功率与传输极限重合。当SCR 小于CSCR 时，LCC-HVDC 无法达到额定运行功率；当SCR 大于CSCR 时，LCC-HVDC 额定运行功率未达到传输极限。考虑额定运行工况下，定电圧控制方式下的CSCR 相较定功率控制方式下的CSCR较小，即VSC-HVDC定交流电压控制方式相较定功率控制方式而言，对LCC-HVDC 传输功率具有更大的支撑强度。

CIGRE 标准直流系统的典型参数T约等于1.5［10］，而对于本文中的修正参数受VSC-HVDC注入功率的影响，进而影响CSCR 的数值，下文将具体分析影响的性质与大小。

3.2 临界值的灵敏度分析

分析VSC-HVDC 运行方式对系统稳定裕度的影响。考虑规划阶段VSC-HVDC 的容量视为常量，将CSCR分别对Pd2与Qd2求偏导可得：

1）VSC-HVDC定功率控制

考虑直流馈入系统的导纳矩阵为对角线占优的负定矩阵［10］，自导纳b22＜0，det(B)＞0，式（24）、式（25）满足：

2）VSC-HVDC定电压控制方式

基于推导得到的功率分岔雅克比矩阵中不含Pd2元素，即Pd2对临界短路比影响较小，由式（26）可得：

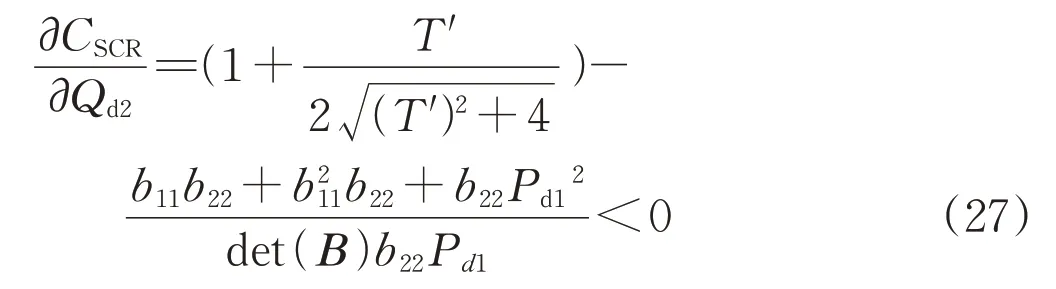
基于式（24）与式（25）的分析结果可知，随着VSC-HVDC 输出的无功功率的增大，T′、T″减小，CSCR 也越小，SCR-CSCR 增大，系统稳定裕度越大；VSC-HVDC 输出的有功功率越大，CSCR 也越大，SCR-CSCR 减小，系统稳定裕度越小。

基于混合直流双馈入系统提出的SCR 机理未来可拓展于多馈入系统。针对混合多馈入系统的电网强度评估，可拓展本文中的稳定机理以及影响因素作用关系。具体地，多馈入系统中VSCHVDC 的注入功率对多馈入系统短路比临界值的影响可以通过文献［20］中的摄动法进行近似分析，然而，文献［20］中的分析方法缺乏实际系统中的物理对象的支撑，仅是一种数值近似手段，未来将研究结构保持的多馈入系统的短路比作用机理以及准确量化该指标临界值跟多馈入系统中VSC-HVDC运行方式以及网络结构的关系。

4 算例分析

4.1 系统模型

本节旨在说明混合直流馈入系统中SCR 及CSCR 指标的有效性。基于PSCAD/EMTDC 与MATLAB仿真软件搭建了如图1所示的系统，其中LCC-HVDC 采用CIGRE 标准直流测试系统参数。表1 为LCC-HVDC 系统参数，表2 为采用定功率控制方式下VSC-HVDC的控制环节参数。

表1 LCC-HVDC系统参数Table 1 LCC-HVDC system parameters

表2 VSC-HVDC控制环节参数Table 2 VSC-HVDC control link parameters

仿真中混合直流馈入系统的直流侧额定功率为1 000 MW，直流侧额定电压500 kV，逆变侧交流系统的额定电压采用线电压有效值230 kV，变压器变比K=211.42/230，交直流电压基准值的比例k=500/230。

4.2 所提指标有效性分析

首先验证2.1 节中CP-CEA 及CC-CEA 两种控制方式下LCC-HVDC 单馈入系统的临界短路比的一致性。基于上文提到的CIGRE标准测试系统，在仿真中分别增大两种控制方式下系统的网络电感值直至系统到达临界稳定。由仿真结果可得，CP-CEA 控制方式下，LCC-HVDC 单馈入临界短路比为2.04；CC-CEA 控制方式下，LCC-HVDC单馈入系统的临界短路比为2.06。即两种控制方式下，LCC-HVDC单馈入系统的临界短路比近似等于2。

以下说明本文提出的SCR 指标用于评估混合直流馈入系统中LCC-HVDC 传输极限的有效性。在仿真模型中控制LCC-HVDC 直流电流指令值以施加功率扰动，仿真中设置直流电流参考值每10 s 增加0.1 p.u.，通过对比不同稳定裕度下的LCC-HVDC功率传输曲线，说明LCC-HVDC功率传输极限与SCR-CSCR的关系。

仿真得到不同稳定裕度下，LCC-HVDC的直流功率传输特性曲线如图3所示。保持仿真系统的SCR 为1.975 恒定，其中case1 表示VSC-HVDC不注入有功无功功率时Pd1随Id1的变化曲线，即Pd2=0，Qd2=0 的运行方式，对应的CSCR=1.975=SCR；case2 表示VSC-HVDC 注入0.15 p.u.的Pd2和0.26 p.u.的Qd2，对应的CSCR=1.968＜SCR；case 3 曲线表示VSC-HVDC 注入0.3 p.u.Pd2的LCC-HVDC 的传输特性，对应的CSCR=1.984＞SCR；case 4曲线表示定交流电压控制方式下VSCHVDC 不注入有功无功功率时LCC-HVDC 的传输特性，对应的CSCR=1.984＜SCR。由图3 case1曲线可知，当SCR=CSCR时，Pd1最大传输功率为1.008 p.u.，最大传输功率对应的Id1为1.012 p.u.，系统的额定运行功率与传输极限近似相等；根据SCR＜CSCR对应的case3曲线可知，系统的最大传输功率0.96 p.u.，对应的直流电流Id1为0.92 p.u.，系统在额定点无法稳定运行，传输极限小于额定功率；根据SCR＞CSCR对应的case2曲线可知，系统传输功率极限为1.08 p.u.大于额定功率，Id1为1.13 p.u.，case3相较case2 VSC-HVDC向换流母线注入更多无功功率，SCR 与CSCR 的差变大，电网强度变大，在系统额定运行点尚未达到功率传输极限，具有一定的稳定裕度。由case 4对应的仿真结果可知，VSC-HVDC定电圧控制方式相较于定功率控制方式对LCC-HVDC具有更好的支撑能力。

图3 不同稳定裕度下，LCC-HVDC的传输特性曲线Fig.3 Transmission characteristic curve of LCC-HVDC under different stability margins

上述分析验证了本文提出的CSCR 指标用于评估混合直流馈入系统中LCC-HVDC 传输极限的有效性。SCR=CSCR为系统的临界稳定条件，此时额定运行点与传输极限点重合。此外，通过SCR与CSCR的差能够表征系统稳定裕度。

4.3 SCR指标临界值的数值误差分析

本节说明考虑VSC-HVDC 的运行方式后，本文提出的SCR 指标的临界值相较其他指标具有更小数值偏差。

计算VSC-HVDC 额定容量为0.5 p.u.时，不同运行方式下的CSCR。仿真得到的CSCR 随VSC-HVDC 注入换流母线功率变化的曲面如图4所示。由图4可知，考虑VSC-HVDC运行方式后仿真得到的CSCR在1.94～2.04区间内，与单馈入LCC-HVDC 的SCR 指标在CIGRE 标准直流系统典型参数下对应的临界值2非常接近，最大数值误差为3%。

图4 临界短路比随VSC-HVDC注入功率变化范围曲面Fig.4 Critical revised short-circuit ratio varies with the injected power of VSC-HVDC

进一步地，将SCR 与文献［12］和［19］中的EESCR 指标及文献［22］的MIESCR（多馈入有效短路比）指标进行比较，以说明本文所提指标具有更小的数值计算误差。EESCR的定义为［12］：

式中：Zij表示节点i与节点j间的等效阻抗。

MIESCR指标的定义表示为［21］：

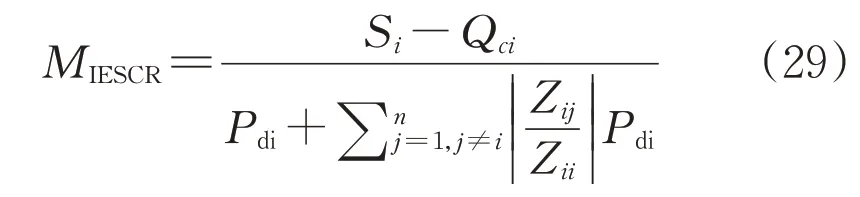
式中：Si表示换流母线i的短路容量；Qci表示母线i的无功补偿量；节点j间的等效阻抗。

基于文献［19］表5的算例，对SCR、MIESCR及EESCR指标临界值进行误差分析，利用仿真得到计算临界值并与其对应的理论临界值计算相对误差，结果如表3 所示。由表3 可知，考虑VSCHVDC 对CSCR 的影响不大，临界值仍接近于2，而VSC-HVDC注入换流母线的功率会影响LCCHVDC 的传输功率极限，从而对MIESCR/EESCR等通过功率等值法得到的短路比指标的临界值造成比较大的数值偏差。CSCR在不同VSCHVDC 运行方式下的变化范围较小，且相较现有的混合直流馈入系统强度评估指标而言，本文所提短路比指标的相对数值误差较小。

表3 指标临界值数值相对误差分析Table 3 Analysis of relative error of index critical numerical value

5 结语

为探究直流馈入系统中VSC-HVDC 接入对LCC-HVDC传输极限的影响，本文基于降阶雅克比矩阵，对现有LCC-HVDC单馈入短路比指标进行修正，得到了适用于评估混合直流馈入中LCCHVDC 系统稳定性的SCR 指标。数学上，所提SCR与混合直流馈入系统中LCC-HVDC的传输极限有着明晰的显函数关系，能够有效量化混合直流馈入系统的静态电压稳定裕度；物理机理上，所提SCR 对应VSC-HVDC 外部电路折算到LCCHVDC交流网络侧的结果。具体分析结果如下：

1）比较了VSC-HVDC 不同运行与控制方式下LCC-HVDC 系统的临界短路比，分析结果表明VSC-HVDC 注入功率对CSCR 影响较小，且VSC-HVDC 在定电压控制方式下更有利于支撑LCC-HVDC的传输功率。

2）基于PSCAD/EMTDC及MATLAB平台给出算例分析，验证了本文提出的短路比指标的有效性。仿真结果表明所提指标的临界值CSCR 相较于现有基于电路等值思想量化混合馈入系统强度的评估指标具有更小的数值误差。