基于粒子群算法的多热源供热系统调节优化

邢鼎皇，王凤霞，王 海

(同济大学 机械与能源工程学院，上海 200092)

1 概述

供热系统调节方式有质调节、量调节、质量调节、间歇调节等。基于准确的水力热力工况分析，以费用最小为目标的质量调节优化已成为学者研究的重点。Jiang等人[1]建立了一种综合利用风能、太阳能、天然气的区域供热系统模型，建立了具有复杂操作约束的最优控制策略的目标函数，利用群搜索优化算法(Group Search Optimizer，GSO)确定了热源最佳供水温度和循环泵最优流量。Wang等人[2]在考虑环境因素的前提下，建立了确定性模型和随机模型，并提出一种改进的粒子群优化算法(Particle Swarm Optimization，PSO)处理经济负荷分配与电力调度。Wang等人[3]建立了分布式循环泵供热管网模型，利用遗传算法寻优热源供水温度和流量，并利用遗传算法设定每个热力站的最优流量，以达到更经济的运行和更短的响应时间。王培红等人[4]将运筹学优化方法与汽轮机组的特性方程结合起来，提出多维动态规划模型，应用于解决汽轮机组的热、电负荷优化分配。

部分国外学者提出的调节优化方法在国内多热源供热系统的应用效果不佳，而国内鲜有学者将现代智能算法应用于多热源供热系统调节方式优化。

本文提出采用混合均值中心反向学习粒子群优化算法(PSO-HMC算法)[5]，考虑供热管道热损失，以供热成本(主要为热源热费、电费)最小作为目标，对多热源供热系统调节方式(质调节、量调节、质量调节)进行优化。结合算例，在用户热负荷一定条件下，对3种调节方式的优化结果进行比较分析。

2 理论基础

2.1 算法原理

粒子群优化算法(PSO)是一种人工智能算法，于1995年由Kennedy和Eberhart共同提出[6-7]。该算法从鸟群捕食行为中获得启发，核心是利用粒子的信息共享从而影响所有粒子在求解空间中从无序到有序地收敛，最终找到问题的最优解。

为实现对粒子所在区域精准搜索，引入混合均值中心进行贪心选择。为避免粒子陷入局部最优解，使粒子散落在更多新区域，对混合均值中心进行反向学习，扩大搜索区域，提高种群全局搜索能力[5]。

2.2 仿真计算理论

为克服传统水力计算方法的局限，越来越多的学者提出新的仿真计算方法。王海等人[8-12]提出的基于网络元求解大型热网水力热力工况的方法，适用于复杂拓扑结构热网。该方法将所有元件分为属性、方法、事件。所有元件根据物理关系建立子模型，将热源、循环泵、阀门、管件、管段、热用户定义为不同元件。属性包括元件的固定设备参数与热网运行的水力热力参数，通过方法建立符合物理规律的控制方程，通过事件表现边界条件[13]。管道热损失根据文献[14]方法进行计算，仅考虑供热管道与土壤的传热，不考虑供回水管道温度场互相叠加的影响。

3 优化模型

多热源供热系统调节目的是在保证可及性的前提下，通过改变多热源供热量比例实现最低成本。某多热源供热系统有L个热源、m个热力站，基于质调节、量调节、质量调节方式分别提出相应的优化模型。

3.1 质调节方式

质调节方式下热源的质量流量保持不变，仅改变热源供水温度以满足热负荷需求。这种调节方式的优点是系统的水力工况比较稳定，但必须保持一定质量流量。质调节优化模型的决策变量为热源供水温度，在用户热负荷一定条件下，热源循环泵耗电量保持不变。

质调节方式优化模型的目标函数Fc为：

(1)

式中Fc——质调节方式优化模型的目标函数，元

L——热源数量

Qi——热源i供热量，GJ

fi,h——热源i热价，元/GJ

Ei——热源i循环泵耗电量，kW·h

f——电价，元/(kW·h)

热源供水温度受热源类型影响，存在最大温度、最小温度限制：

θi,min≤θi≤θi,max

(2)

式中θi,min、θi,max——热源最小、最大供水温度，℃

θi——热源i供水温度，℃

热源供热量为用户用热量与管道热损失之和：

(3)

式中Qu——用户用热量，GJ

Qpip——管道热损失，GJ

受热源性质影响，热源供热量存在最小供热量与最大供热量限制：

Qi,min≤Qi≤Qi,max

(4)

Qi=3.6×10-3qm,icp(θi,s-θi,r)t

(5)

式中Qi,min、Qi,max——热源i最小、最大供热量，GJ

qm,i——热源i质量流量，kg/s

cp——热水比定压热容，kJ/(kg·K)

θi,s、θi,r——热源i供、回水温度，℃

t——时间，h，取1 h

3.2 量调节方式

量调节方式通过调节热源循环泵，改变热网质量流量，不改变热源供水温度。这种调节方式可降低热源循环泵耗电量，但因水力工况不断变化，系统稳定性比较低。与单热源的量调节方式不同，多热源量调节方式优化模型涉及多热源流量比例组合，可使节能空间进一步增大。

虽然热源供水温度确定，但供热成本并不确定，这是由于各热源的质量流量不同，末端回水温度也不同，导致管道热损失存在差别。在用户热负荷一定条件下，量调节方式优化模型的决策变量为热源质量流量，目标函数与式(1)相同。

除满足式(2)～(5)的约束外，量调节方式优化模型对热源循环泵的流量、扬程提出了新的约束。为避免汽蚀，循环泵实际质量流量不得低于额定质量流量的30%。受零件强度限制，循环泵实际质量流量不得超过最大质量流量。为满足热力站资用压头，并确保系统不超压，循环泵扬程应控制在最小、最大扬程范围内。

3.3 质量调节方式

质量调节方式同时改变热源供水温度与质量流量，以满足热负荷需求。这种调节方式既可减少热源循环泵耗电量，又可避免管网水力热力失调，但调节难度比较高。在用户热负荷一定条件下，质量调节方式优化模型的决策变量为热源供水温度、质量流量，目标函数与式(1)相同。除满足式(2)～(5)的约束外，热源循环泵还要满足质量流量、扬程约束。

3.4 优化模型仿真计算步骤

本文提出的优化模型属于无解析解的数学优化问题，传统的优化方法如线性规划、非线性规划难以解决，而PSO-HMC算法对于求解复杂高维的优化问题非常有效。

以质量调节方式优化模型为例，基于PSO-HMC算法的优化模型仿真计算流程见图1。

PSO-HMC算法中的适应度函数值对应目标函数，算法的维度对应决策变量数，粒子位置对应热源供水温度与质量流量的组合，算法的最佳位置对应使目标函数最小的热源参数。优化模型仿真计算分为以下步骤。

① 输入边界条件。热力站预测热负荷、系统定压点压力、最不利末端资用压头。

② 初始化参数。设定粒子群的种群数量为N，种群的搜索空间维度为2L+m。初始化参数包括热力站预测质量流量、热源预测质量流量、热源预测供水温度。设定迭代次数为X，对个体学习因子c1、社会学习因子c2、惯性权重ω赋值。

③ 调用热网仿真计算程序得到各粒子位置下的热源循环泵耗电量、热源供热量。热网仿真计算程序基于王海等人提出的网络元方法[8-12]。

④ 计算粒子的适应度函数值Y。

⑤ 判断是否达到迭代次数，若达到则输出最优解，即目标函数最小时热源供水温度、热源质量流量。否则采用粒子群算法更新粒子位置，返回步骤③重新计算。

4 案例分析

4.1 案例概况与设定

案例为某多热源供热系统，拓扑结构见图2。多热源供热系统有3个热源、20座热力站。其中，热源A供热能力为16 MW，热源B供热能力为20 MW，热源C供热能力为22 MW。热源供水温度范围为60～120 ℃。供暖室外计算温度为-9 ℃时，热源设计供、回水温度为90、65 ℃。供热管道规格涵盖DN 100～1 200 mm，保温层厚度根据文献[15]选取，工作管热导率为46.5 W/(m·K)，保温层热导率为0.033 W/(m·K)，土壤温度设定为5 ℃。

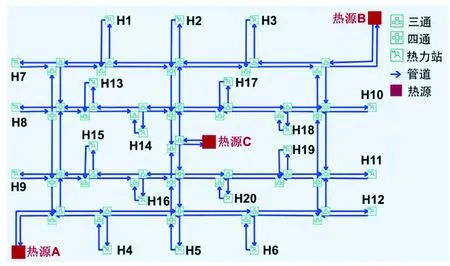
图2 多热源供热系统拓扑结构(软件截图)

边界条件：根据各热力站供热面积，按照供暖热指标40 W/m2[16]计算各热力站预测热负荷(见表1)。设定系统定压点压力为热源A的回水压力(0.3 MPa)，保持最不利热力站H11资用压头为40 kPa。

初始化参数：根据热力站预测热负荷，按照供回水温差20 ℃计算预测质量流量(见表1)，计算结果取整数。按表1计算热力站总预测质量流量，根据各热源供热能力按比例分配各热源预测质量流量，计算得到热源A预测质量流量为118.6 kg/s，热源B预测质量流量为148.3 kg/s，热源C预测质量流量为163.1 kg/s。各热源预测供水温度取供暖室外计算温度对应的90 ℃。种群数量N为50，迭代次数X为50步，个体学习因子c1、社会学习因子c2均为2，惯性权重ω为0.5[6-7]。

热源A～C热价均为40 元/GJ，电价为0.55 元/(kW·h)。热源循环泵耗电量、热源供热量均以供热系统运行1 h计算。

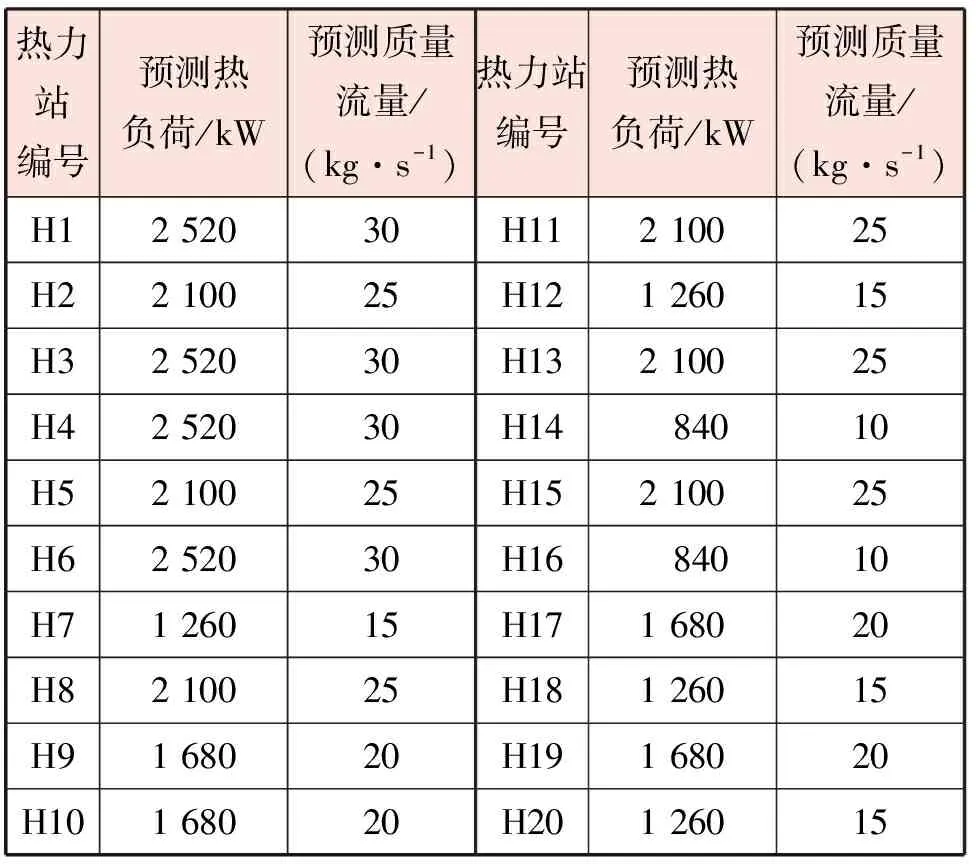
表1 各热力站预测热负荷、预测质量流量

4.2 优化结果

① 质调节方式

质调节方式优化模型的优化结果见表2。由优化结果可知，质调节方式下，热源总热功率为38.86 MW，管道热损失为2.74 MW，占比约7.05%。热源A～C供热量比例分别为26.9%、34.1%、39.0%。

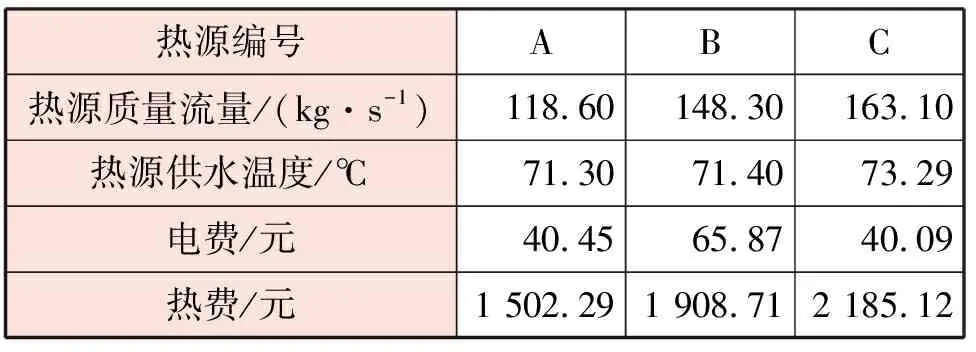
表2 质调节方式优化模型的优化结果

② 量调节方式

量调节方式优化模型的优化结果见表3。由优化结果可知，量调节方式下，热源总热功率为39.04 MW，管道热损失为2.92 MW，占比约7.48%。热源A～C供热量比例分别为21.3%、23.3%、55.4%。

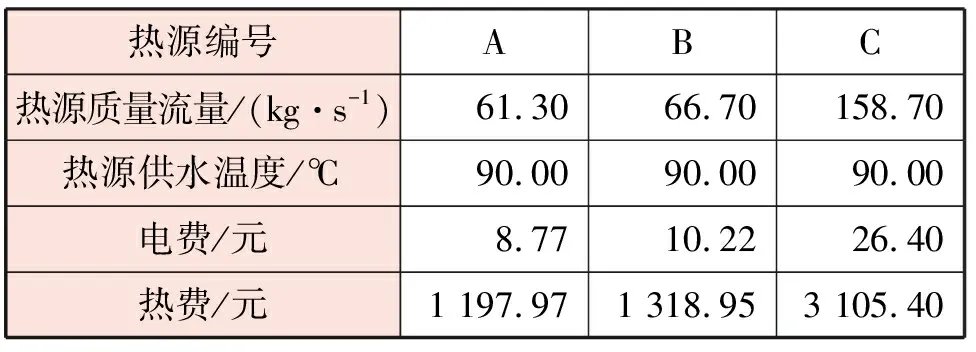
表3 量调节方式优化模型的优化结果

各热力站预测热负荷不变，分析热源供水温度对量调节方式优化模型优化结果的影响。不同热源供水温度下量调节方式优化模型的优化结果见表4。由表4可知，电费随热源供水温度增大而减小(主要由供回水温差加大造成)，热费随热源供水温度增大而增大(主要由管道热损失增大造成)，但二者总和变化不大。分析电费、热费随热水供水温度变化趋势可知，二者的变化符合常理，说明PSO-HMC算法的仿真计算结果可信。量调节方式下，采用不同热源供水温度时，热源A～C供热量比例的变化不大，热源A供热量比例变化范围为21.3%～23.4%，热源B供热量比例变化范围为23.2%～26.2%，热源C供热量比例变化范围为51.1%～55.4%。

③ 质量调节方式

质量调节方式优化模型的优化结果见表5。由优化结果可知，质量调节方式下，热源总热功率为39.01 MW，管道热损失为2.89 MW，占比约7.41%。热源A～C供热量比例分别为23.4%、26.5%、50.1%。

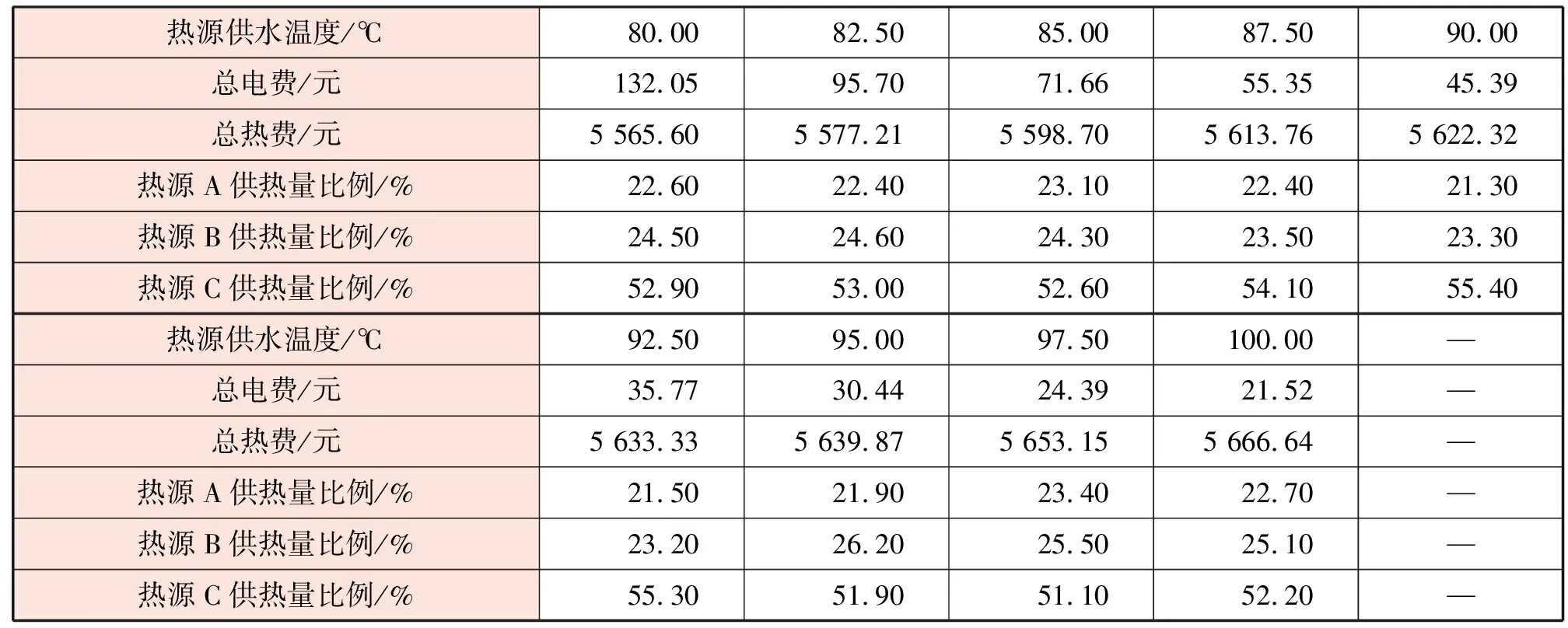
表4 不同热源供水温度下量调节方式优化模型的优化结果

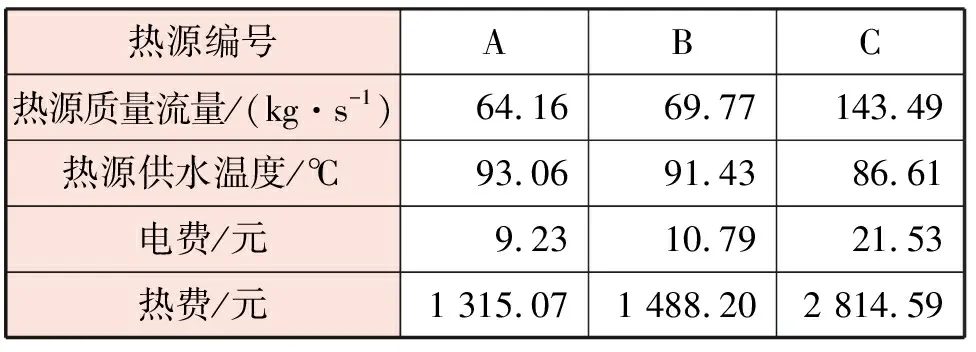
表5 质量调节方式优化模型的优化结果

4.3 对比分析

用户热负荷一定时，质量调节方式的供热成本最低，量调节方式居中，质调节方式最高。

用户热负荷一定时，对于多热源供热量比例，量调节方式与质量调节方式接近。

5 结论

① PSO-HMC算法的优化模型仿真计算结果可信。

② 用户热负荷一定时，质量调节方式的供热成本最低。

③ 由优化结果可知：用户热负荷一定时，对于多热源供热量比例，量调节方式与质量调节方式接近。量调节方式下，采用不同热源供水温度时，热源A～C供热量比例的变化范围不大。