基于彩色图像Tetrolet变换的频数质心零水印算法

张天骐, 叶绍鹏, 刘鉴兴, 柏浩钧

(1. 重庆邮电大学通信与信息工程学院, 重庆 400065; 2. 重庆邮电大学信号与信息处理重庆市重点实验室, 重庆 400065)

0 引 言

数字通信的快速发展使得数字图像在互联网上非法复制与传播,容易导致版权的欺诈问题。数字水印是证明版权所有的有力途径之一,其在宿主图像中秘密嵌入被称为“水印”的所有者信息[1]。传统的数字水印通常采用修改空间域或变换域系数的方法嵌入水印。如,文献[2]将图像进行分块处理,根据每一个子块的奇偶性来设置嵌入规则,将水印信息嵌入其中;文献[3]提出了一种基于快速沃尔什-哈达玛变换(fast Walsh-Hadamard transform, FWHT)、奇异值分解(singular value decomposition, SVD)的盲水印算法,该算法不可见性和鲁棒性欠佳。文献[4-5]都选择了修改轮廓波变换后的系数嵌入水印。上述算法对图像数据造成不同程度的改变,然而,水印的不可见性和抗攻击能力是相互制约的。在文献[6]中作者给出了一种通过使用载体图片的特征生成零水印的方案,该方法在没有改变载体图片数据特征的情形下就实现了嵌入水印的目的,并且较好地处理了不可见性和鲁棒性差的问题。

通常大多数零水印算法都是结合不同变换域,提取载体图像中的特征数据来获得特征矩阵。文献[7]介绍了一种双零水印方案,该方法首先利用Douglas-Peucker算法提取矢量地图的特征顶点和非特征顶点,然后构造Delaunay三角网格形成特征顶点的拓扑特征序列和SVD矩阵形成非特征顶点的固有特征序列,该方案综合了特征信息和非特征信息,提高了水印的容量,但是鲁棒性提升并不明显。文献[8]中提出一种针对彩色图像的零水印算法,首先将彩色图像分离3个通道(R、G、B)对应的3幅图像和一幅灰度图像。然后构造出两组三维张量。接着利用SVD-离散余弦变换(SVD-discrete cosine transform, SVD-DCT)在三维张量中提取特征矩阵生成零水印。该方案具有一定的创新性,并未提高鲁棒性。熊祥光[9]提出了一种空间域的零水印算法,根据空间域的子块均值与整体均值的关系构造零水印。该算法大幅度提高了图像处理攻击的鲁棒性。文献[10]利用轮廓波变换和奇异值分解以及Hu不变量实现鲁棒性,具备良好抗噪性能,但是在几何攻击方面表现不佳。文献[11]利用Curvelet变换,奇异值分解提取图像特征,提出一种子块映射机制生成零水印的方法。该算法获得较强的鲁棒性,但该算法是基于灰度图像设计的。现有的基于彩色图像的零水印算法不够丰富,或是对某种攻击的鲁棒性有一定的提高,但对较为复杂的攻击,鲁棒性仍有待提升。上述零水印算法结合多种变换域,而Tetrolet变换由Krommweh[12]在2009年提出,兼顾小波变换与轮廓波变换的优势,文献[13]利用传统的水印算法修改Tetrolet系数,所获得效果并不佳,不可见性差,而且抗噪性能不高。但Tetrolet在零水印系统中的应用几乎还是一片空白。

基于此,本文结合Tetrolet变换,提出一种利用非负矩阵分解(nonnegative matrix factorization, NMF)分解,统计图像的频数质心特性,并采用信息编码的规则对水印加密的新型零水印算法。

1 Tetrolet变换与NMF分解

1.1 Tetrolet变换

Tetrolet变换由Krommweh[12]提出,是基于对Haar小波的改进,采用类似于“俄罗斯方块”自适应的方式填充四格拼板。该变换方法充分考虑了轮廓波变换等多尺度多分辨率分析的优点,能较全面考虑图象的几何特性,能较稀疏地描述图象,从而使得能量系数比较集中,在图像压缩,噪声抑制,特征提取等方面均有不错的效果。Tetrolet变换算法步骤如下:

(1) 对图像I0进行4×4分块,每块为Qi, j(i,j=0,1,…,N/2r+1-1)。

(2) 对每块Qi, j采用四格拼版的形式进行填充,一共有117种方式。最基础的4个拼版具有5种形式,如图1所示。若不考虑旋转与镜像,有22种填充方式,如图2所示。

图1 5种基本四格拼版
Fig.1 Five basic four-collages

图2 22种基本填充方式Fig.2 22 basic filling methods

(1)

(2)

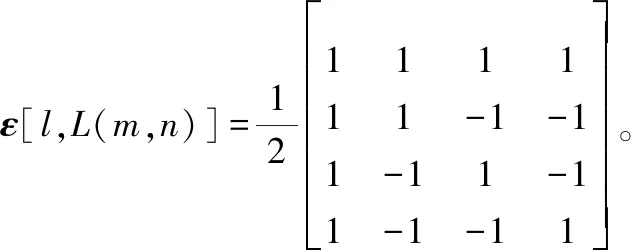
(4) 将低频系数重新进行排列,作为下一级的输入,重复上述步骤直至分解到r级结束。

Tetrolet变换的详细过程可参考文献[12-14]。Tetrolet变换使图像得到的低频系数能量更加集中,应用于水印系统,能提高水印的鲁棒性和抗噪能力。

1.2 NMF分解

NMF分解最早由Lee和Seung于1999年在《Nature》上提出,用于人脸识别。NMF应用于数字水印系统具有以下特点:① 分解结果非负,恰好满足灰度值非负的条件,具有明确的物理意义,同时对高维数据的降维处理提高了运算速度。② 能挖掘数据本身的特征结构而不改变数据结构[15]。NMF可以描述为,对任意一个给定非负矩阵V,总能有非负矩阵W,H使得:

Vn×m=Wn×rHr×n+ε

(3)

式中:W为基矩阵;H为系数矩阵;r为预设参数,满足

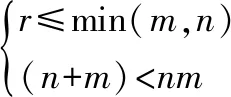
(4)

步骤 1对基矩阵W和系数矩阵H随机赋初值。

步骤 2根据式(3)对基矩阵W和系数矩阵H进行更新:

(5)

式中:Hkj是第(k-1)r+j次循环结果;Wik是第(i-1)n+k次循环结果。

步骤 3重复步骤2至收敛,即可得到最优的基矩阵W和系数矩阵H。

2 Polar码与二维交织

2.1 Polar码编码

Polar码是根据Arikan[16]通过信道产生的极化现象提出来的,而按照信道极化理论,Polar码在理论上能到达最大信道容量。在二进制输入的离散无记忆通道中,经过信道极化后,信道被分割为纯噪信道和无噪信道,在无噪信道中传送消息比特,在纯噪信道中传输预置的冻结比特。

Polar码符合二元线性分组码的基本特性,编码由信息位和生成矩阵决定。编码过程如下:

(6)

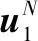
(7)

式中:GN(A)代表GN中A集对应的行构成的生成矩阵;⊕为异或符号;Ac为A的补集。极化码的编码可以由如下参数确定:码长N,信息位A,信息位的个数K,K/N为码率,冻结位uA,通常置为“0”符号,故表示为P(N,K,A,uAc)。

2.2 二维交织算法

二维交织技术是将图像以交织单元的形式进行置乱,将成串的错误分散到图像的各个区域。交织技术将错误分散,Polar码对错码进行纠错,二者结合提高水印系统抗突发错误能力。首先把2n×2n的矩阵作为交织的单元,再把这个单位等分为四个象限,每个象限再分四个象限,以此类推,直至分为2×2的最小单元为止。具体构造步骤如下:

先将2×2最小单元里的4个元素按式(8)排列成交织方阵,再按式(9)进行升维得到高阶的交织方阵。

(8)

(9)

式中：0,1,2和3均为2×2的矩阵。

3 零水印的生成与提取

3.1 载体图像的处理

如流程图3所示,对载体图像处理的具体步骤如下:

步骤 1将输入的彩色载体图像(大小为M×M)转化到YCbCr空间,然后分离亮度Y通道,同时对Y分量进行Tetrolet变换,得到其低频系数wlm与高频系数whm。

步骤 2取低频系数wlm进行8×8分块,对每一子块进行NMF分解,得到各子块的一维基向量。

步骤 3依次根据一维基向量构造频数质心,算出每个子块的质心。

步骤 4采用局部阈值生成的方法,计算出每相邻的8×8子块质心值的平均值作为阈值,在这8×8子块质心值中大于阈值设置为1,小于阈值设置0,得到M/8×M/8特征矩阵T。

图3 生成特征矩阵
Fig.3 Generating characteristics matrix

频数质心能够稳定表示图像特征。这里,对步骤3中构造质心频数的过程做详细介绍。一维基向量中数据D={x1,x2,…,xn}映射到x轴上,取最大值为max,最小值为min,将数据分为k组,组距为t,设定子区间[min,min+t),[min+t,min+2t),…,[min+(i-1)t,min+it),…,[min+(k-1)t,max],统计D中数据在各个区间的次数C=[m1,m2,…,mi,…,mk],m1+m2…+mi+…+mk=n,根据公式Xi=min+it-t/2,依次求出各个子区间的中位数,得到对应的中位数序列X=[X1,X2,…,Xi,…,Xk]。根据式(10)求其质心:

(10)

3.2 零水印的生成

零水印生成的过程如图4所示,具体步骤如下:

步骤 1采用reshape的方式将m×m的二值水印图像降维成一维序列,对该序列用Polar码的编码规则N=2m×2m,K=m×m,码率r=1/4的参数进行编码得到wb。再根据式(8)和式(9)进行SP二维交织形成带有水印信息的交织方阵S。

步骤 2将交织方阵S与特征矩阵T进行异或(exclusive OR, XOR)操作生成零水印信息Z注册到版权保护中心。运算方式为

Z=XOR(S,T)

(11)

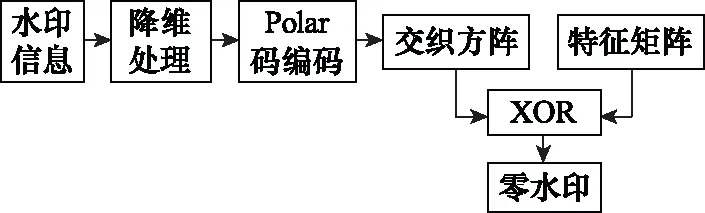
图4 生成零水印Fig.4 Generating zero watermark

3.3 零水印提取

水印的提取与嵌入过程相似,见流程图5,具体步骤如下:

步骤 1将受到攻击的载体图像按第3.1节中步骤2～步骤4的操作,提取出特征矩阵T′。

步骤 2把特征矩阵与零水印Z进行异或操作得到含水印信息的交织矩阵S′。

S′=XOR(Z,T′)

(12)

步骤 3对S′进行去交织,Polar码解码,重构为m×m的图像即可得到版权水印w′。

图5 提取零水印Fig.5 Extracting zero watermark

4 实验仿真分析

如图6所示,仿真实验载体图像选取1 024×1 024的24位真彩色图像,选用32×32的“印”作为二值水印图像。

图6 彩色载体图像与水印图像Fig.6 Color carrier image and watermark image

本文采用归一化相关系数(normalized coefficient, NC)来评估该算法的唯一性和鲁棒性。NC是指提取的水印图像与原始的水印图像之间的相似度。NC的公式如下:

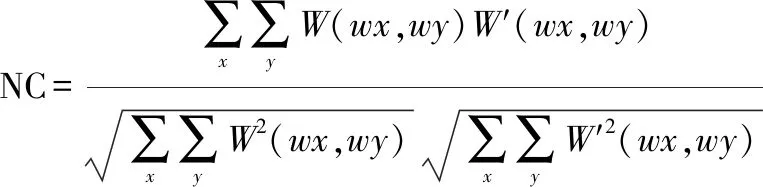
(13)

式中：W(wx,wy)表示原始的水印图像;W′(wx,wy)表示提取的水印图像。

4.1 虚警率实验

由于不同载体图像产生的特征图像不同,不同图像产生的特征矩阵也应该不同,即不同图像产生的零水印之间的相关性应该相对较小。因此,为了验证不同载体图像之间的虚警率,对实验图像进行两两测试,NC值越高,说明虚警率越高,实验结果如表1所示。从表1可以看出,当提取水印的图像与原始载体图像一致时,算法都能将水印完整的提取出来;当提取水印的图像与原始载体图像不一致时,所提取水印最高NC值为0.685 4,如图7所示,从图中也难获取与原始水印的信息。因此,本文算法具有较低的虚警率与良好的安全性。

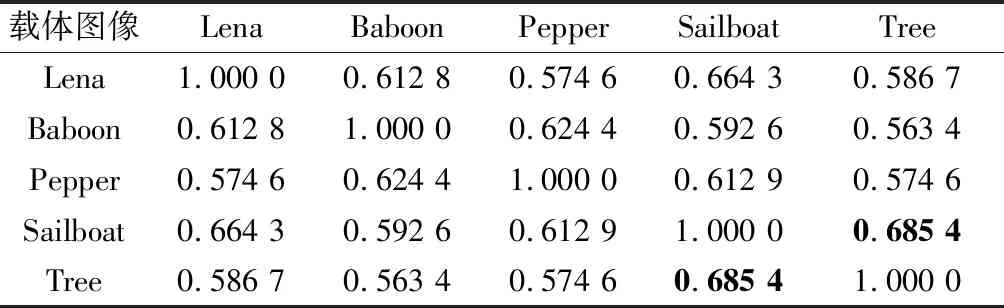
表1 虚警率检测的NC值

图7 表1中NC=0.685 4的水印图像Fig.7 Watermark image with NC=0.685 4 in Table 1

4.2 鲁棒性检测

4.2.1 非几何攻击

非几何攻击是常规的图像处理方式对图像的像素值进行修改,并未修改其相对位置。为测试本文算法在非几何攻击下的鲁棒性,分别对4幅载体图像添加高斯噪声、椒盐噪声、泊松噪声攻击,攻击的参数均值为0,方差为0.1和0.5;采用模板大小为3×3,9×9的均值滤波,维纳滤波和高斯低通滤波分别进行攻击;JPEG压缩因子为10、30、50进行攻击。

由表2可以看出,这4幅载体图像在不同类型、不同强度的噪声攻击下,NC值最低在0.93以上。对于滤波攻击和压缩攻击,大部分NC值几乎为1,说明本文算法能有效抵抗非几何攻击。

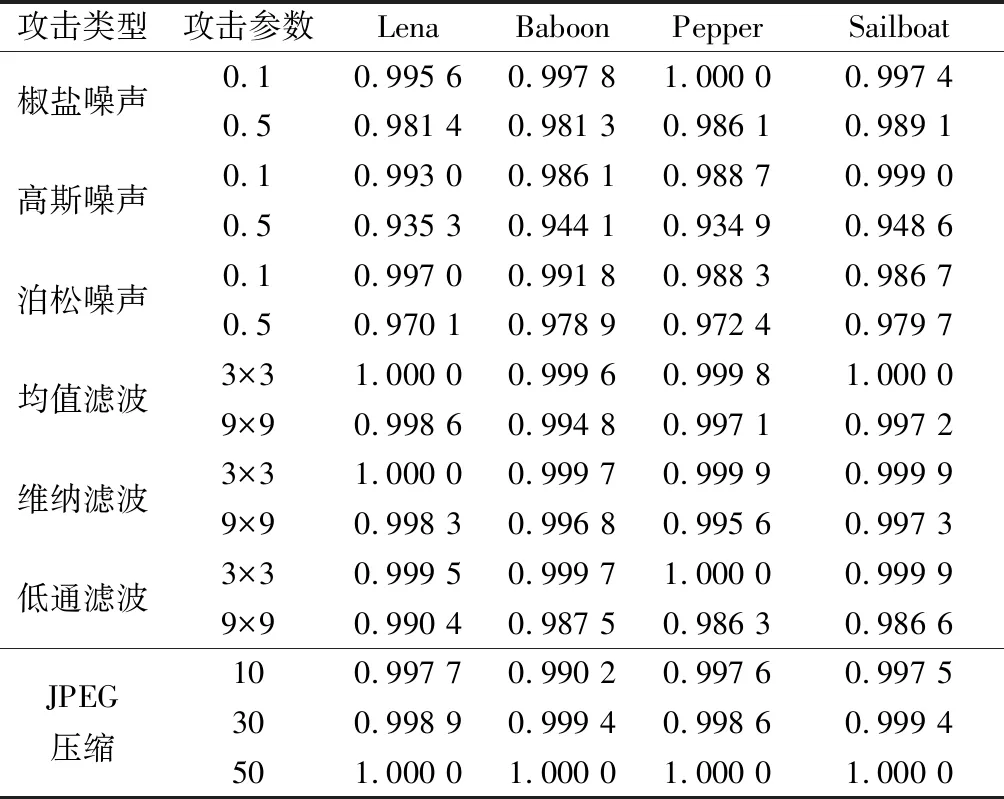
表2 非几何攻击实验的NC值

4.2.2 几何攻击

几何攻击对图像的特征改变较大,通常情况下会同时改变像素值与像素的相对位置。为检验本文算法对几何攻击的鲁棒性,对这4幅图像采用旋转攻击、剪切攻击、行列偏移攻击,实验结果如表3所示。为验证Polar码编码+二维交织算法能抵抗突发错误,优化水印系统性能,对Lena图像进行剪切攻击,采用加入交织算法与未加入交织算法的方式进行对比,提取效果如图8所示。

由表3可得,旋转攻击对图像影响较大,在旋转10°的条件下NC值仍在0.9以上。对于行列偏移攻击会使图像整体位置发生改变,在偏移20列时,本文算法仍然能将水印信息较好的恢复,NC值均在0.95以上。对于剪切攻击,在剪切1/4以内具有不错的鲁棒性,如果剪切面积变大,会造成数据大量丢失,难以提取图像特征。故本文算法在几何攻击下也具有不错的鲁棒性。如图8所示,图8(d)～图8(f)是采用Polar编码在图8(a)～图8(c)中所提取的水印,图8(h)～图8(j)采用Polar编码+二维交织算法在图8(a)～图8(c)中所提取的水印。可以明显看出,未用交织算法所提取的水印容易出现突发错误,加入交织技术后所提取的水印信息明显清晰,NC值提高,故Polar编码+二维交织算法能够对水印信息进行纠错,防止突发错误,达到增强抗几何攻击的能力。

表3 几何攻击实验的NC值

图8 未交织与交织提取水印对比Fig.8 Comparison of uninterleaved and interleaved watermarks

4.2.3 组合攻击与其他攻击

为进一步验证本文算法的鲁棒性,采用以下攻击方式进行测试,实验结果如图9所示。其中攻击的参数设置如下:① 高斯噪声(均值为0,方差0.1)+剪切攻击(中心剪切1/4);② 均值滤波(模板大小为9×9)+旋转攻击(10°);③ 直方图均衡化+旋转攻击(5°)+行列偏移(向下10行,向右10列);④ 篡改攻击(中心剪切1/4);⑤ 8×8马赛克攻击。图9(a)～图9(e)所提取的水印分别对应图9(f)～图9(j)。由图9(a)～图9(e)可以看出,组合攻击使得图像质量变差,但水印提取较为清晰。对于马赛克攻击和1/4篡改攻击也有良好的提取效果。本文采用Tetrolet变换和NMF分解统计频数质心能稳定的提取特征矩阵,另加上Polar的纠错能力,因此能很好地恢复水印信息。

图9 不同攻击方式与提取的水印Fig.9 Different attack methods and extracted watermarks

4.3 对比实验

选取Lena载体图像,将本文算法与近年来具有代表性的文献[8]中所提基于变换域的零水印算法,以及文献[9]中所提空域强鲁棒零水印算法进行对比。分别采用均值为0的高斯噪声攻击、均值滤波攻击、JPEG压缩、旋转攻击、行列偏移攻击、剪切1/4攻击,实验结果如图10所示。

在非几何攻击方面,选取常见的加噪,滤波,压缩攻击。如图10(a)所示,3种算法随着噪声强度的增加,所提取水印NC值均呈下降趋势,本文算法所提取NC值下降趋势较为缓慢,且都高于其他两种算法。对于滤波与JPEG压缩攻击,如图10(b)、图10(c)所示3种算法均有良好的鲁棒性,NC都在0.96以上,但就变化趋势而言,更加能凸显本文算法的稳定性;即使在11×11模板滤波下或压缩因子为10的JPEG压缩下,本文算法所提取水印NC依然更接近1。对于几何攻击,选取具有代表性的旋转、剪切、平移攻击方式。如图10(d)所示,对于平移与旋转攻击,随着旋转角度的增大,本文算法下降趋势较为稳定,且NC值均高于其他二者。对不同区域剪切攻击方面,本文算法所提取水印NC值略低于其他两种算法,但NC值也在0.9以上。综上所述,就整体而言本文算法鲁棒性优于其他二者。

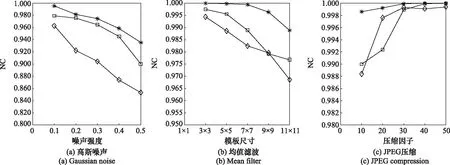
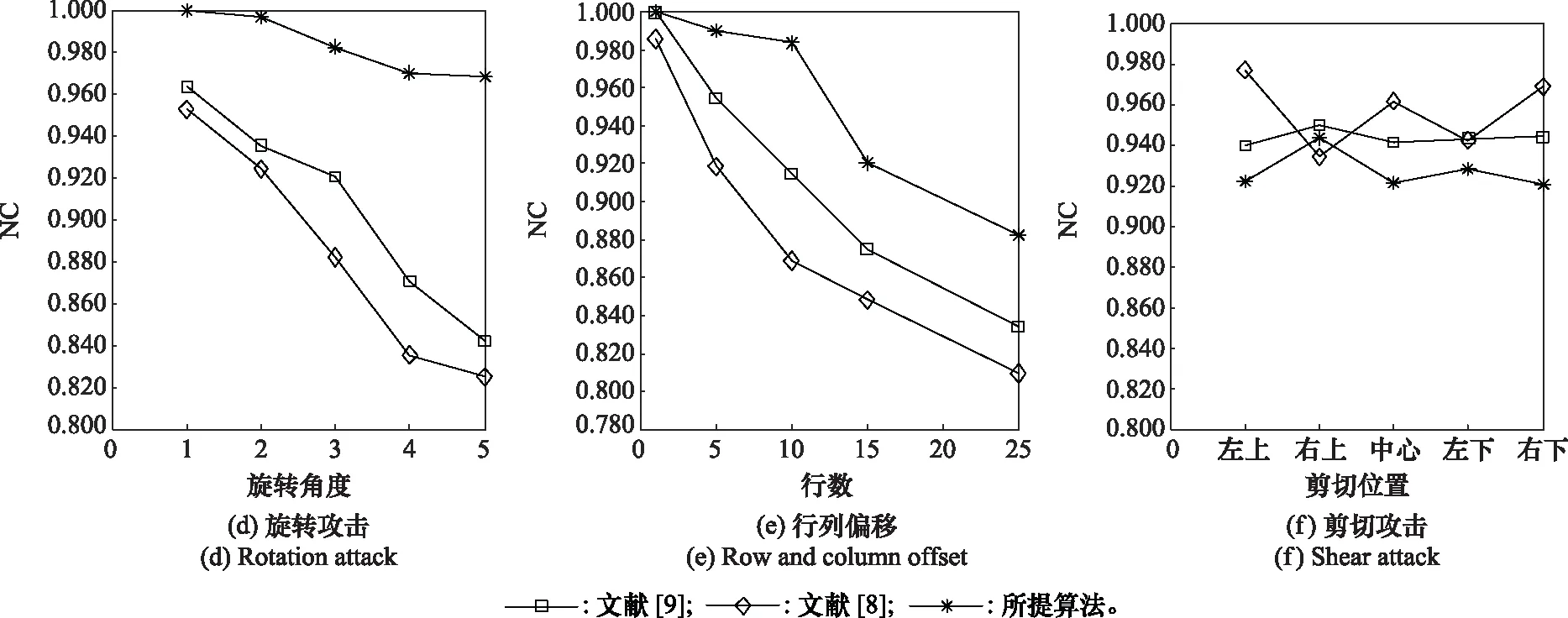
图10 不同算法对比结果Fig.10 Comparison of different algorithms

5 结 论

在无损的要求下进行版权保护,本文设计了一种基于彩色图像Tetrolet的频数质心算法,能根据图像的统计与局部特征,稳定地提取图像特征;将Polar码和交织算法与零水印系统结合,在水印提取时能避免突发错误并具有纠错能力,能更好地提取水印。经大量仿真实验验证,本文算法具有良好的鲁棒性和抗几何攻击能力。因此,可以广泛地应用在数字产品的版权保护中,在接下来的工作中,我们将致力于降低算法的复杂度,并将所提算法扩展到视频零水印算法中。