基于岭回归正则极限学习机的OFDM系统信道估计
2023-02-09袁伟康解志斌杨紫薇
袁伟康,解志斌,陈 磊,杨紫薇
(江苏科技大学 海洋学院,江苏 镇江 212003)
0 引言
正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)是在频域内将信道分成若干正交子信道,将串行数字信号转换成许多并行的数据信号流,并分别调制到每个子信道上进行传输的一种传输方式。目前,通常需要执行高阶调制,以达到提高传输速率的目的,这对于OFDM系统的信道估计的时效性和精确性提出了更高的要求。
现有的OFDM系统信道估计方法主要有非盲信道估计和盲(半盲)信道估计。在非盲信道估计的方法中,最小二乘(Least Squares, LS)算法计算简单、复杂度低,不需要信道的任何先验信道信息,在实际中被广泛使用[1]。然而,由于需要通过插值获取信道状态,导致LS算法的估计性能较差。文献[2]提出的线性最小均方误差(Linear Minimum Mean Square Error, LMMSE)算法优于LS算法,但是需要信道的先验统计信息,且计算复杂度较高。基于压缩感知的信道估计方法,则被广泛认为可以从稀疏性角度优化导频资源的同时,保证信道估计的MSE性能[3-4]。在盲(半盲)信道估计方法中,为了减少资源的开销,文献[5]提出一种基于预编码的修正联合盲信道估计算法,文献[6]则提出一种基于变分贝叶斯推断的半盲信道估计算法。盲与半盲信道估计的方法相比,节省了频谱资源,但是估计性能较差。
近年来,利用不同神经网络进行信道估计的方法也成为研究热点。信道估计在系统的角度来看,可作为一个寻找非线性回归的问题,并将信号国通信道传输视为一个数学过程。同时,多径信道的系统可以建模为一个自回归问题,并且这个问题可以很好地适用于频域选择性衰落的信道模型[7]。因此,信道估计的问题就转变为求解自回归系数的问题,通过确定网络自回归系数,进而得到网络模型进行信道估计。文献[8]采用长短时记忆网络(Long Short-term Memory, LSTM),在信道估计中学习信号之间相关性并进行预测,达到提高整体估计性能的目的,但是存在估计速度慢的不足。文献[9]提出了一种利用极限学习机进行信道估计的方法,解决了其他神经网络中的迭代时间过长等问题,但是会产生网络权值矩阵无法求解的情况。
本文提出了一种基于岭回归正则极限学习机(Regularization Extreme Learning Machine, RELM)的OFDM信道估计算法,改进了一个基于极限学习机的信道估计网络模型,在损失函数中增加L2范数,使损失函数正则化,再利用岭回归算法求解极限学习机的输出层状态参数,得到一个适用于信道估计网络的回归模型,从而避免发生权值矩阵无法求解的情况。同时,与反向传播网络相比,省去训练过程中迭代的大量时间。同时利用神经网络可以学习得到回归模型权值矩阵的最优解。
1 系统模型
1.1 OFDM系统模型
考虑设计一个OFDM系统,如图1所示。假定导频信号及其状态已知。
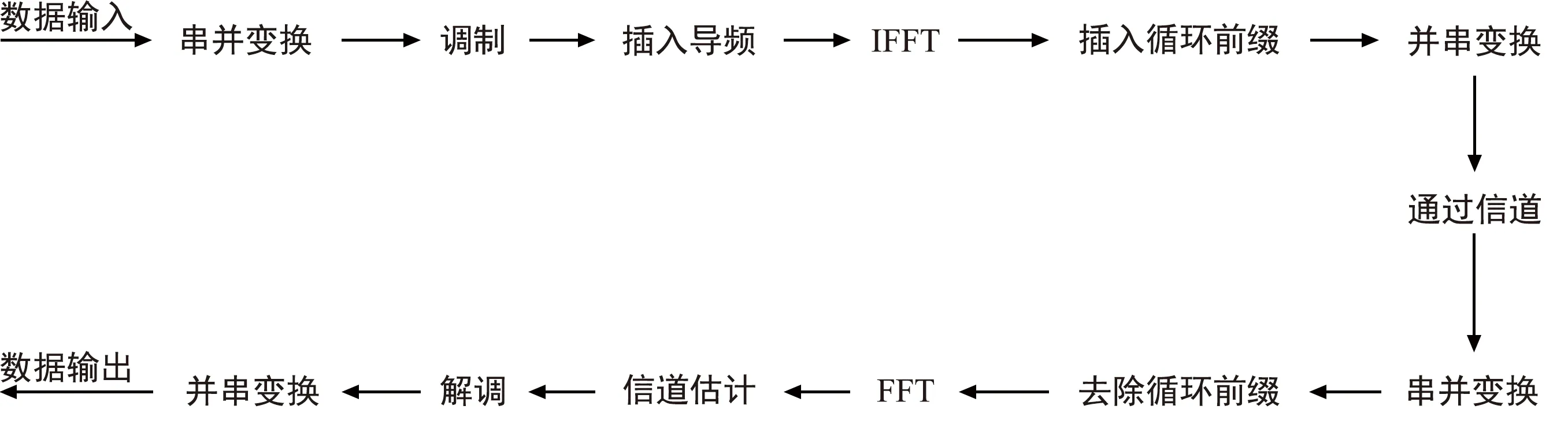
图1 OFDM系统框图
在一个OFDM符号时间内,令子载波上导频处信道响应向量为h=[h(1),h(2),…,h(Np)]T。其中,第k个子载波上导频的符号为x(k),令发送矩阵为X=diag[x(1),x(2),…,x(Np)],此时,接收符号向量为:
y=X·h+z,
(1)
式中,z表示高斯白噪声,服从N(0,σ2)分布。
1.2 网络模型
极限学习机(Extreme Learning Machine, ELM)属于一种新型的单隐层前馈神经网络,具有学习速度快、泛化性好、鲁棒性强等特点[10-12],其基本原理图如图 2 所示。
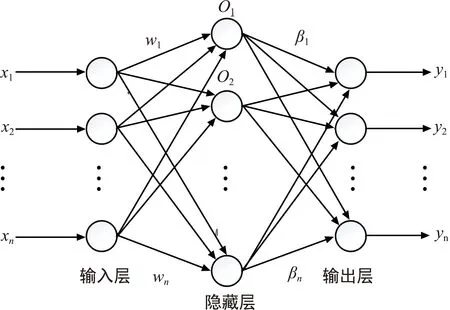
图2 ELM神经网络模型图
针对一个含有n个输入神经元,i个隐含层神经元和m个输出层神经元的单隐层网络,其数学模型可以表示为:
Hβ=T,
(2)
式中,
(3)
式中,H为随机特征映射矩阵,wi=[ωi1,ωi2,…,ωin]T是隐含层神经元的连接权值,bi是隐含层神经元的偏差(bias),βi=[βi1,βi2,…,βim]T表示隐含层与输出层之间的的权值权重,T表示理想输出,g(x)为激活函数。
隐含层神经元参数(wi,bi)通过任意概率分布随机生成,因此,隐含层的输出矩阵H实际上是已知的,且在保持不变。式(1)转化成了求解线性方程Hβ=Τ的最小二乘解:
(4)
式中,H†表示隐含层输出矩阵H的广义逆。
2 基于岭回归RELM的信道估计
本节提出了一种基于岭回归RELM的OFDM信道估计算法,其系统结构如图3所示。
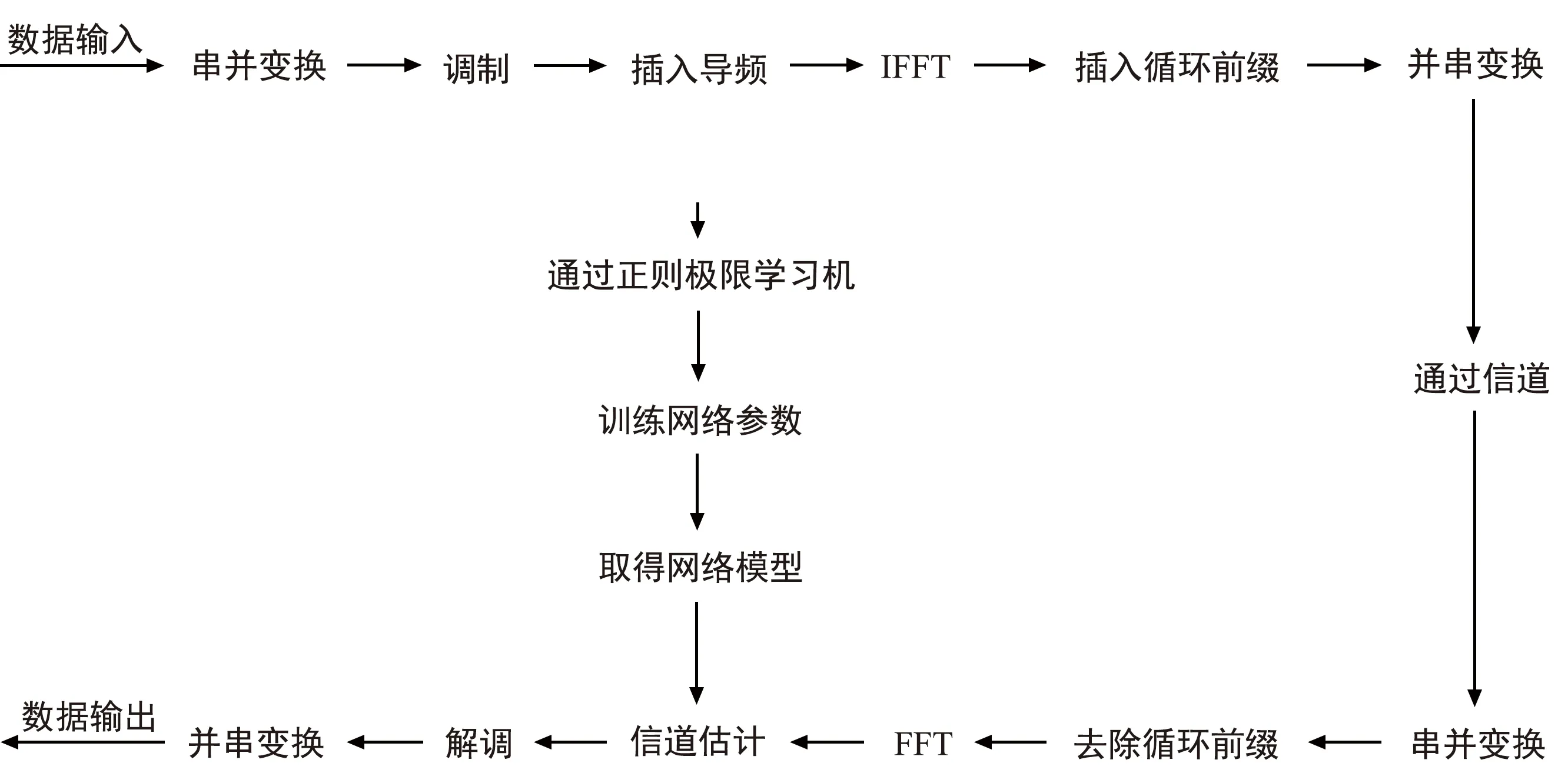
图3 岭回归RELM信道估计系统结构模型图
训练阶段根据映射数据确定初始的训练集:
Di={(xi,ti)|xi∈Rn,ti∈Rn},其中xi表示导频发送信号,ti表示接收端导频信号,i=1,2,…,n。本文选用Sigmiod函数为激活函数,表达式为:
(5)
在训练过程中,由系统随机产生输出层和隐含层之间的连接权值矩阵wi和隐藏层节点的偏置矩阵bi,对于输入的数据进行预处理,神经网络函数可以通过βi,wi,bi,xn表示为:
(6)
常规极限学习机隐含层到输出层间的权值矩阵常采用求逆解出,但由于传输矩阵可能出现不满秩,从而产生对传输矩阵无法求逆等情况,影响网络权值矩阵的求解[13-15]。针对这一问题,本文在单隐层至输出层的环节增加L2范数,使其损失函数正则化,从而取得更符合实际、更可靠的回归矩阵,对于病态数据的拟合更强。
传统极限学习机的输出层损失函数为:
(7)
通过加入惩罚因子构成的L2范数α‖β‖2,得到正则化损失函数为:
(8)
式中,α为惩罚因子,α∈(0,1)。令式(8)为0,此时所需输出层传递矩阵β*可以表示为:
(9)
利用岭回归方法,对式(8)进行求导,可以得到:
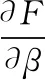
(10)
当式(10)等于0时,可以得到:
β*=(XTX+αI)-1XTT,
(11)
式中,β*为适合该信道估计网络的最优输出矩阵权值。
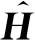
(12)
式中,Φ表示信道估计网络对信号的处理过程。
3 评估准则与复杂度分析
3.1 评估准则
本文通过误码率(Bit Error Rate, BER)以及信道估计均方误差(Mean Square Error, MSE)来评价所提算法估计质量[16]。令H*表示信号的实际状态矩阵,则信道估计均方误差表达式为:
(13)
3.2 算法复杂度分析
表1对LS信道估计算法、LMMSE信道估计算法、基于BP的信道估计算法以及基于岭回归RELM的信道估计算法在一个OFDM符号时间的信道估计过程中的复杂度进行了比较,其计算以进行一次乘积运算的次数为参考[17]。

表1 算法复杂度比较表
由表1可以看出,基于BP和岭回归RELM的信道估计算法在各连接层之间只需要进行简单的乘法运算,复杂度与LS信道估计算法相当,但均低于LMMSE信道估计算法[18]。特别地,对比基于BP与基于RELM的信道估计算法,由于BP算法需要通过迭代对网络权值进行修正,从而达到设定的阈值并结束训练。而岭回归RELM算法可以在给定随机生成初始值的情况下直接求解得到网络的信道参数,因此,其训练时间远低于BP算法。
4 仿真与分析
为了评估所提算法性能,本节将不同网络参数下的岭回归RELM网络信道估计BER与MSE性能进行仿真分析,同时还选取了基于岭回归RELM、ELM、BP的信道估计算法,以及传统LS信道估计算法,在相同仿真参数下对于BER和MSE性能进行进一步对比,本文在Matlab 2020a环境下进行仿真。
本文所构建的网络模型层数为3层:输入层、隐含层和输出层,每层神经元的个数为分别为16、128、16。系统样本数量为30 000,其中80%作为训练数据集,20%作为测试数据集。系统的仿真参数设置如表2所示。
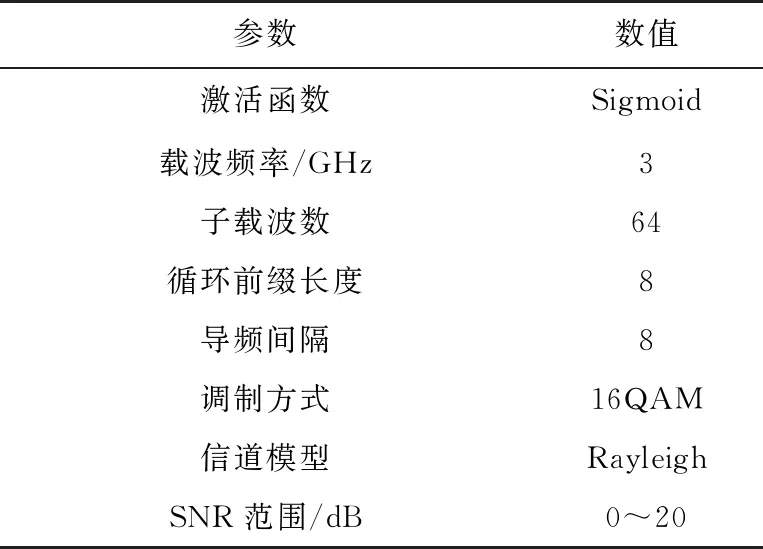
表2 系统参数设置表
图4展示了LS算法,基于ELM、BP以及岭回归RELM的信道估计算法在不同信噪比下的MSE性能。
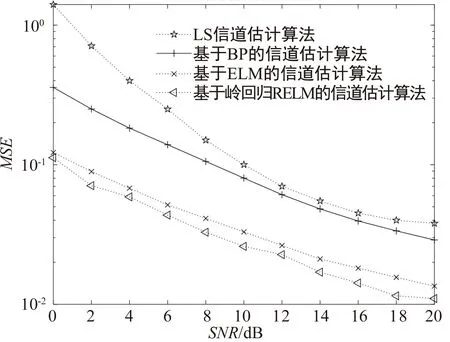
图4 不同信道估计方法的MSE性能对比图
由图4可以看出,不同估计方法的MSE性能随着SNR的增加都呈现下降的趋势,其中,本文所提出的基于岭回归RELM的信道估计算法MSE性能具有明显的优势,而LS算法性能最差。由分析可知, LS算法信道估计过程中是忽略了噪声的影响,所提算法与基于BP的信道估计算法相比,可以获得神经网络输出层权值函数的全局最优解,因此估计阶段可以取得更优的估计性能。本文所提算法在训练阶段利用L2正则化,与基于ELM的信道估计算法相比,可以实现更高鲁棒性,更好地拟合出回归模型,因此具有最好的估计性能。
图5给出了不同信噪比情况下,4种信道估计方法的BER性能图。由图5可知,随着信噪比的提高,误码率均呈现出下降的趋势。在高信噪比的情况下,本文提出的信道估计算法具有明显的优势。在20 dB时,本文所提出算法误码率为1×10-3,而LS算法则为3.5×10-2,基于BP的信道估计算法为0.6×10-2,基于ELM的信道估计算法为1×10-2。
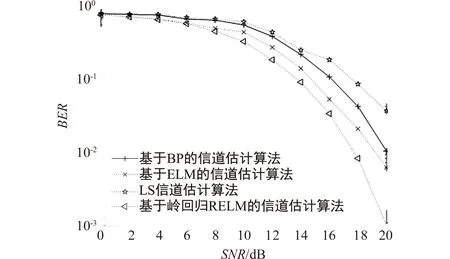
图5 不同估计方法下的BER性能对比图
由图6可以看出,在改变导频数量的情况下,本文所提算法的MSE性能均随着信噪比的提高而提高。同时,导频数量越多,本文所提算法在相同信噪比的情况下,MSE性能越好。但导频数量的增加也会引起频谱资源占用过多的情况。
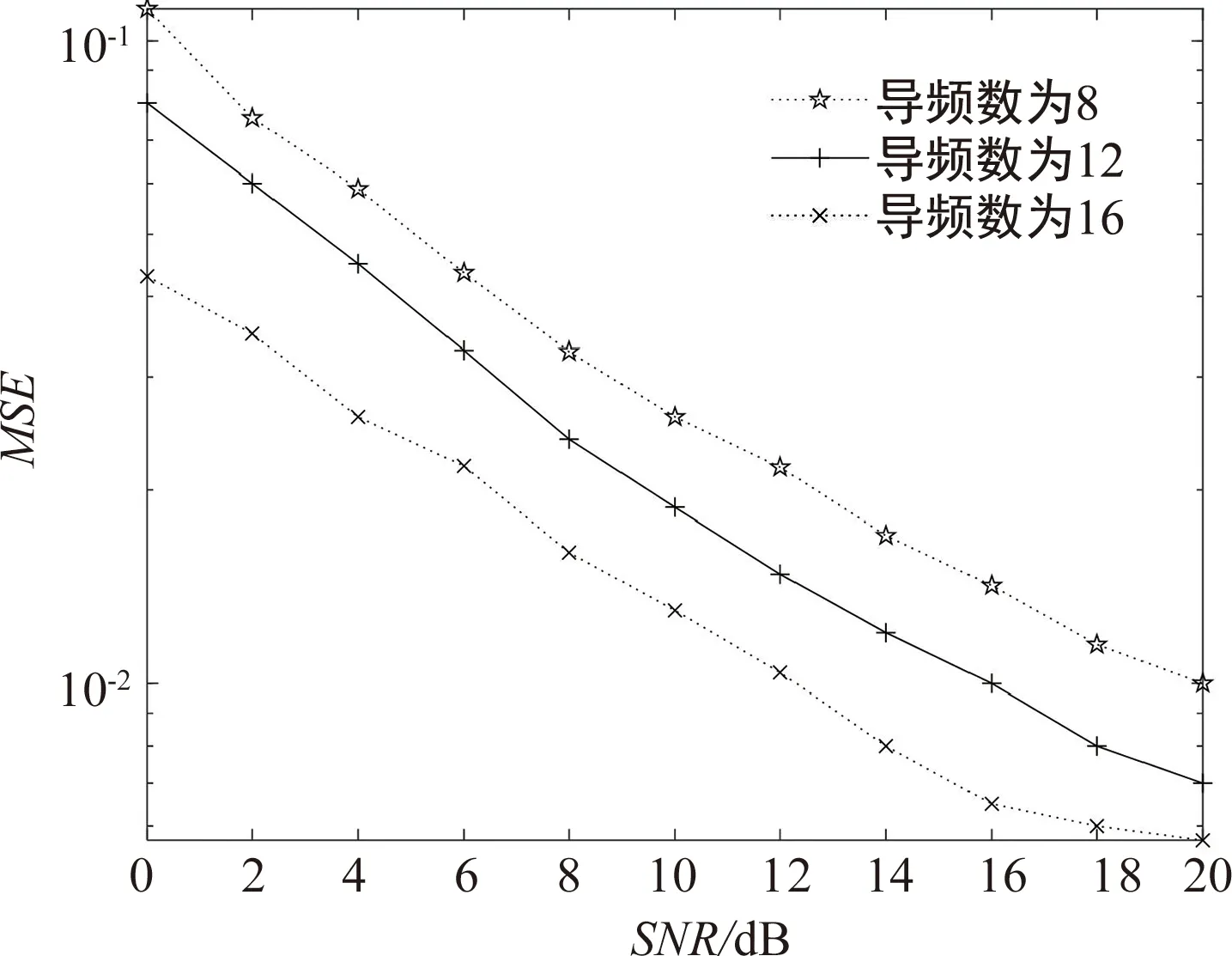
图6 不同导频数量时的MSE性能对比图
图7展示了导频数量分别为8、12、16情况下本文所提算法的误码率情况,从图中可以看出,随着导频数量的增多,所提算法误码率降低。但是,导频数量过多会导致频带利用率下降。因此,在系统设计中,需要对BER的性能要求和频带利用率进行综合考量。
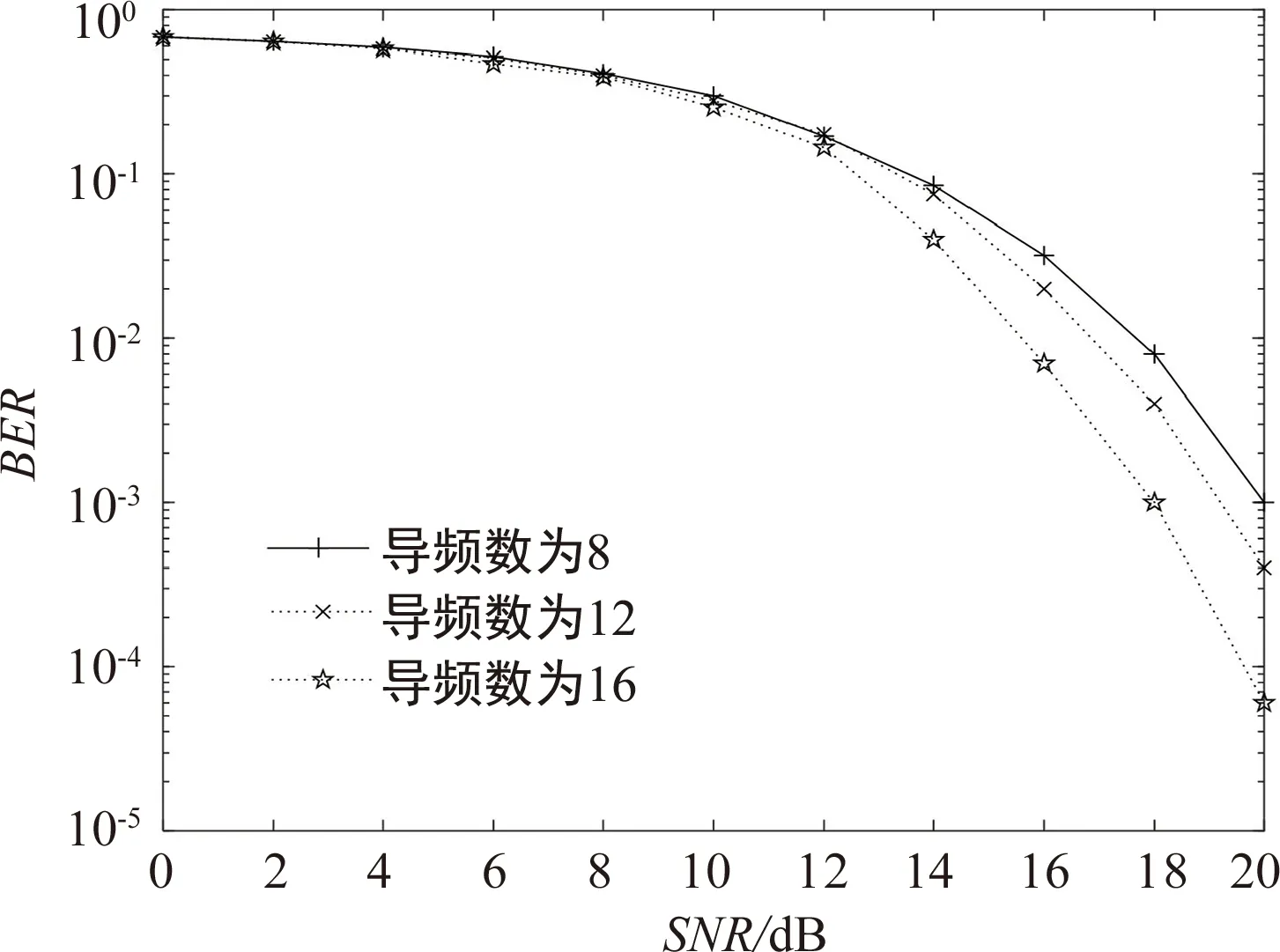
图7 不同导频数量时的BER性能对比图
5 结束语
为了进一步改善OFDM信道估计性能,本文提出了一种基于岭回归RELM的信道估计算法。改进算法可以解决传统极限学习机权值参数无法求解的问题。同时,所提算法通过岭回归优化极限学习机,取得最优的输出矩阵权值参数,进而完成信道估计。由仿真结果可以明显看出,相较于LS算法、基于BP的信道估计算法以及基于ELM的信道估计算法,本文所提算法可以实现更低的系统均方误差,达到更低的误码率,具有更高的估计准确度。
