OCDM系统抗衰落性能分析
2023-02-09詹涛,雷霞
詹 涛,雷 霞
(电子科技大学 通信抗干扰技术国家级重点实验室,四川 成都 611731)
0 引言
线性调频波(Chirp)指频率随着时间线性变化的传输信号波,目前已经在多个领域中被发现并广泛应用。例如,近场菲涅尔衍射的空间频率就随着衍射点到屏幕中心的距离线性增加[1-2],而在雷达系统中线性调频波被广泛应用于测距和定位[3-4]。事实上,线性调频波因为有类扩频的效果,对于无线通信系统中的一些不利因素,如多径衰落有着较强的抵抗能力[5]。
基于线性调频波的特点,许多科研工作者致力于将其拓展到通信领域。文献[5-7]将扩频技术和线性调频波相结合,提出了一种线性调频扩频技术,该技术具有安全性高、鲁棒性强的特点,因而被应用于军事通信、水下通信以及航空航天通信等领域。但是,在线性调频扩频或线性调频调制系统中,其频谱效率由于其扩频特性较低,因而很长一段时间内线性调频波都用于低数据率的传输场景。
为了增加宽带系统的传输效率,文献[8]提出了一种多频道传输技术。该技术通过将整个带宽分割给一系列频谱分离的线性调频波,以此来防止多调频波之间的干扰。该技术虽然避免了调频波之间的相互影响,但是每个载波带宽都较窄,因而抗干扰能力并不是很强。
在此背景下,文献[9]提出了一种正交线性调频复用(Orthogonal Chirp Division Multiplexing, OCDM)技术,该技术构造了一组相互正交的线性调频波,以此作为并行子载波来承载数据,接收端通过匹配滤波恢复原始信号。同时,该文献基于离散菲涅尔变换分析了OCDM系统的数字实现原理[10]。此后,文献[11-12]分别研究了OCDM传输模式在光纤通信和水下通信领域的传输能力。作为一种新型的宽带多载波传输方式,对OCDM系统在不同场景下抗衰落能力的研究及与传统基于OFDM的宽带传输方式的对比俨然成为当下的一个热点。
现有文献对OCDM系统的峰均比和不同循环前缀(Cyclic Prefix, CP)长度下的系统性能进行了分析[9],但对其抗衰落特性还缺乏系统讨论。因此,本文详细研究了OCDM系统、传统OFDM及DFT-Precoded-OFDM系统在不同多径数目、不同多普勒扩展以及不同循环前缀(Cyclic Prefix, CP)长度下的传输性能。通过数字仿真和分析,验证了OCDM系统由于在时域和频域都有符号扩展的效果,故具备对多径干扰和多普勒扩展都更鲁棒的传输能力,有望成为未来宽带多载波传输在恶劣信道中的一类备选波形。
1 OCDM系统调制收发原理
给定某一线性调频波的形式为:
(1)
式中,T表示线性调频波持续时间,N为正整数。以ψ0(t)为基波进行时移,可以得到一组线性调频波,其中第k个线性调频波的表达式为:
(2)
可以证明,这样的一组线性调频波是相互正交的,即
(3)
基于式(3)所示的一组相互正交的线性调频波,可以得到OCDM系统一般的调制原理。如图1所示,设x=[x(0),x(1),…,x(N-1)]T表示数字基带调制后的符号向量,将x进行串并转换后,每个符号调制到对应的线性调频波上进行传输,则传输信号为:
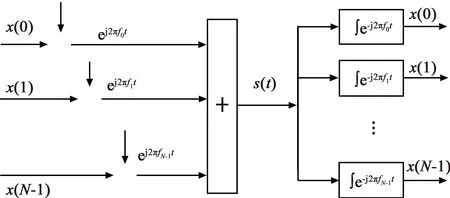
图1 OCDM系统传输原理示意图
(4)
由于并行传输数据的子载波之间相互正交,所以在接收端可以采用匹配滤波的方式得到对应的发送数据,即
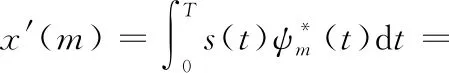
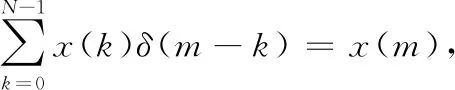
(5)
由此便实现了OCDM系统在理论上的调制与接收[9]。
2 OCDM系统发送端调制的数字实现
上节给出了OCDM系统调制和接收的基本原理,基于该原理可以在理论上证明OCDM的可行性,但由于此时系统的复杂度与复用的多载波数目成正比,并不具备实际意义。
研究证明,如离散傅里叶变换是OFDM系统低复杂度数字实现的关键类似,离散菲涅尔变换(Discrete Fresnel Transform, DFnT)也是OCDM系统数字实现的关键[9]。
DFnT的具体形式与阶数N的奇偶性有关,不失一般性,本文只考虑N为偶数的情况。对于式中给出的发送信号s(t),在t=nT/N处进行采样可得:
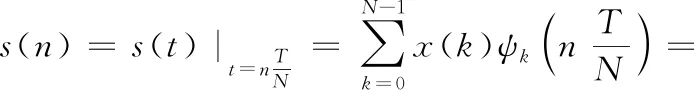
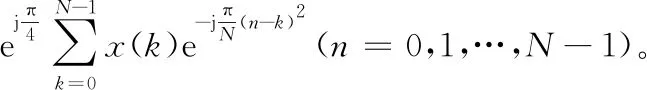
(6)
由于DFnT矩阵的数学形式为:
(7)
该矩阵为循环酉矩阵,离散菲涅尔反变换(Inverse Discrete Fresnel Transform, IDFnT)是该矩阵的共轭转置。
观察式(6)可得,采样后的发送信号s(n)可通过对原始数据x(k)做IDFnT后得到,即
s=ΦHx。
(8)
值得注意的是,IDFnT矩阵可以由IDFT矩阵经相位旋转得到[9],说明可以基于FFT算法实现式,其有效降低了OCDM系统实现的复杂度,使该系统具备了实用价值。
3 OCDM系统接收端检测技术
信号通过信道的过程就是信号与信道衰落系数线性卷积的过程。类似于OFDM,OCDM系统也可以通过循环前缀的引入,不仅消除符号间干扰(ISI),同时令线性卷积转变为圆周卷积。
设x为基带调制后的符号向量,H为信道时域衰落系数对应的循环矩阵,则接收端接收到的经过衰落信道后的信号为:
r=HΦHx+n,
(9)
式中,n表示高斯白噪声向量。
设信道状态信息已知,下面给出OCDM系统的一种低复杂度的频域均衡方式[9]。对式中的接收信号做DFT可以得到:
Ωr=ΩHΦHs+Ωn,
(10)
式中,Ω表示DFT矩阵。设ΩH表示IDFT矩阵,利用I=ΩHΩ将公式改写为如下形式:
Ωr=ΩHIΦHIs+Ωn=ΩHΩHΩΦHΩHΩs+Ωn,
(11)
令G=ΩHΩH,T=ΩΦHΩH。因为H、ΦH都为循环矩阵,所以G、T都是对角矩阵且矩阵T为定值。
为恢复发送信号,考虑到矩阵T的逆必然存在,首先可以消除矩阵T:
T-1Ωr=T-1GTΩs+T-1Ωn。
(12)
因为对角矩阵相乘可以交换位置,所以上式即为:
T-1Ωr=T-1TGΩs+T-1Ωn=GΩs+T-1Ωn。
(13)
进一步,为消除由信道决定的矩阵G的影响,接收端需要在等式两边同乘均衡矩阵Λ:
ΛT-1Ωr=ΛGΩs+ΛT-1Ωn。
(14)
由于迫零(Zero Force, ZF)均衡存在放大噪声的问题,所以本文采用最小均方误差(Minimum Mean Square Error, MMSE)均衡,则均衡矩阵Λ为:
(15)
式中,ρ表示信噪比。
最后由IDFT变换得到恢复出来的信号为:
(16)
综上,OCDM系统的数字实现框图如图2所示,同时,传统OFDM系统以及DFT-Precoded-OFDM系统的原理框图分别如图3和图4所示。
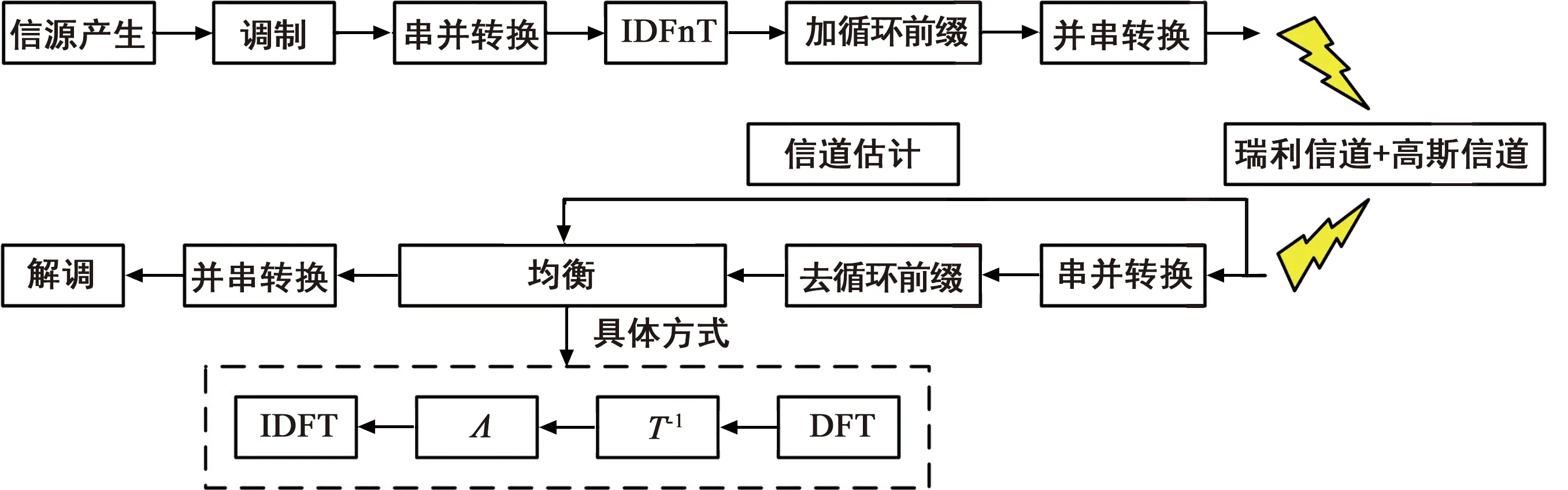
图2 OCDM系统的数字实现框图
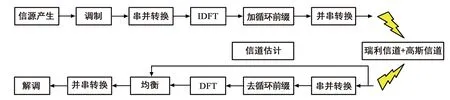
图3 传统OFDM系统的数字实现框图

图4 DFT-Precoded-OFDM系统数字实现框图
4 数字仿真及分析
4.1 不同时延扩展条件下的比较
为了研究不同时延扩展对不同宽带传输系统的影响,约定三种传输系统子载波数均为1 024,调制方式为16QAM,均衡方式为MMSE,为公平起见,DFT-Precoded-OFDM系统的DFT预编码点数也为1 024,信道条件如表1所示,其中,情况三为经典EVA信道,情况二是EVA只截取前五径的情况,多普勒扩展统一为1 Hz。

表1 针对多径数目的仿真条件
根据表1所示仿真条件,得到仿真结果如图5所示。从图5可以看到,在表1所示仿真条件下,单径和五径两种情况下的三种系统误码性能基本一致;而对于九径的情况,OCDM 系统与 DFT-Precoded-OFDM系统误码性能基本一致,二者均优于传统 OFDM 系统。
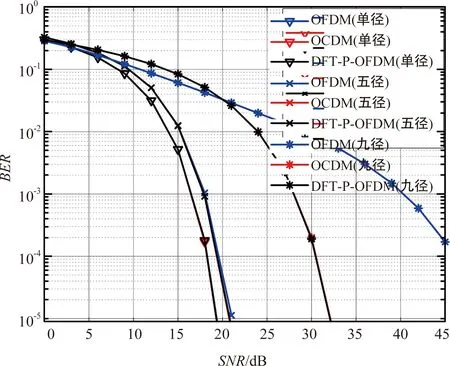
图5 针对多径数目的仿真结果图
进一步对信道的相关带宽进行分析可得:单径情况下信道相关带宽足够宽,信道不存在频率选择性衰落;在五径和九径的情况下,信道最大时延扩展σmax分别为370 ns和2 510 ns。因此,九径条件下的信道更容易出现频率选择性衰落并且衰落程度更大。
频率选择性衰落会对宽带传输带来影响,但对于OCDM系统和DFT-Precoded-OFDM系统而言,由于其传输符号所用的子载波本质上是一个宽带信号而具备类扩频的效果,因而可以获得更强的抗频域选择性衰落的能力,误码性能更优。
4.2 不同多普勒扩展条件下的比较
为了研究多普勒扩展对不同宽带多载波传输系统的影响,考虑单径信道,无时延,调制方式为16QAM,均衡方式为MMSE均衡,子载波数目为1 024,设置归一化多普勒扩展分别为3.4×10-4,3.8×10-3和0.2。
根据上述仿真条件,得到仿真结果如图6所示。
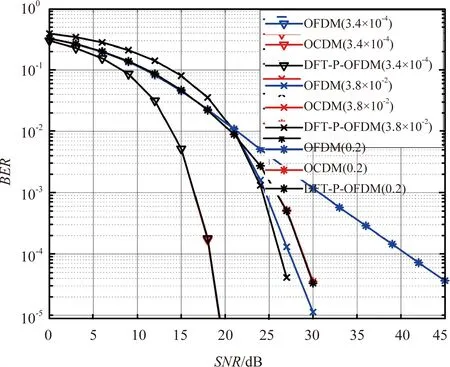
图6 针对多普勒频移的仿真结果图
从图6可以看出,在单径情况下,如果多普勒扩展较小,与预期一致,三种系统误码率基本相当。
随着多普勒扩展的增加,OCDM 系统与 DFT-Precoded-OFDM 系统的误码性能仍能保持,且均优于传统 OFDM 系统。分析其原因为:当多普勒扩展增加,传统OFDM系统的子载波间干扰将明显增加,而OCDM和 DFT-Precoded-OFDM 系统将衰落的影响分散到整个带宽上,因而削减了衰落的影响。
4.3 不同循环前缀长度的对比
为了充分研究 OCDM 系统的抗多径干扰的能力,考虑在一些较为极端的情况下测试三种系统的误码性能。从对OFDM系统的分析可知,添加 CP 的作用之一是为了消除 ISI。在本节中,设置不同的 CP 长度,仿真测试循环前缀不足时三种系统的误码性能,以此来研究三种系统抗 ISI能力的大小。系统条件统一为子载波数目1 024,调制方式QPSK,均衡模式MMSE。信道条件选择典型的EVA信道(如表1所示,情况三),多普勒扩展统一为1 Hz。依据信道最大多径时延,其对应的CP长度为7.53,选择5、7、9三种典型CP长度进行仿真对比。
根据上述仿真条件,得到仿真结果如图7所示。从图7中可以看到,由于最大多径时延对应的 CP 长度为 7.53,当系统设置的 CP 长度为7时,DFT-Precoded-OFDM 系统的误码性能已经出现严重衰减,而OCDM 系统的误码性能仍保持在与 CP 足够的情况下几乎一致的水平,这说明OCDM 系统抗ISI干扰能力更强。当然,在 CP 长度进一步缩短为 5 时,两种系统的误码性能均出现严重衰退,但OCDM还是维持和OFDM接近的抗ISI能力。
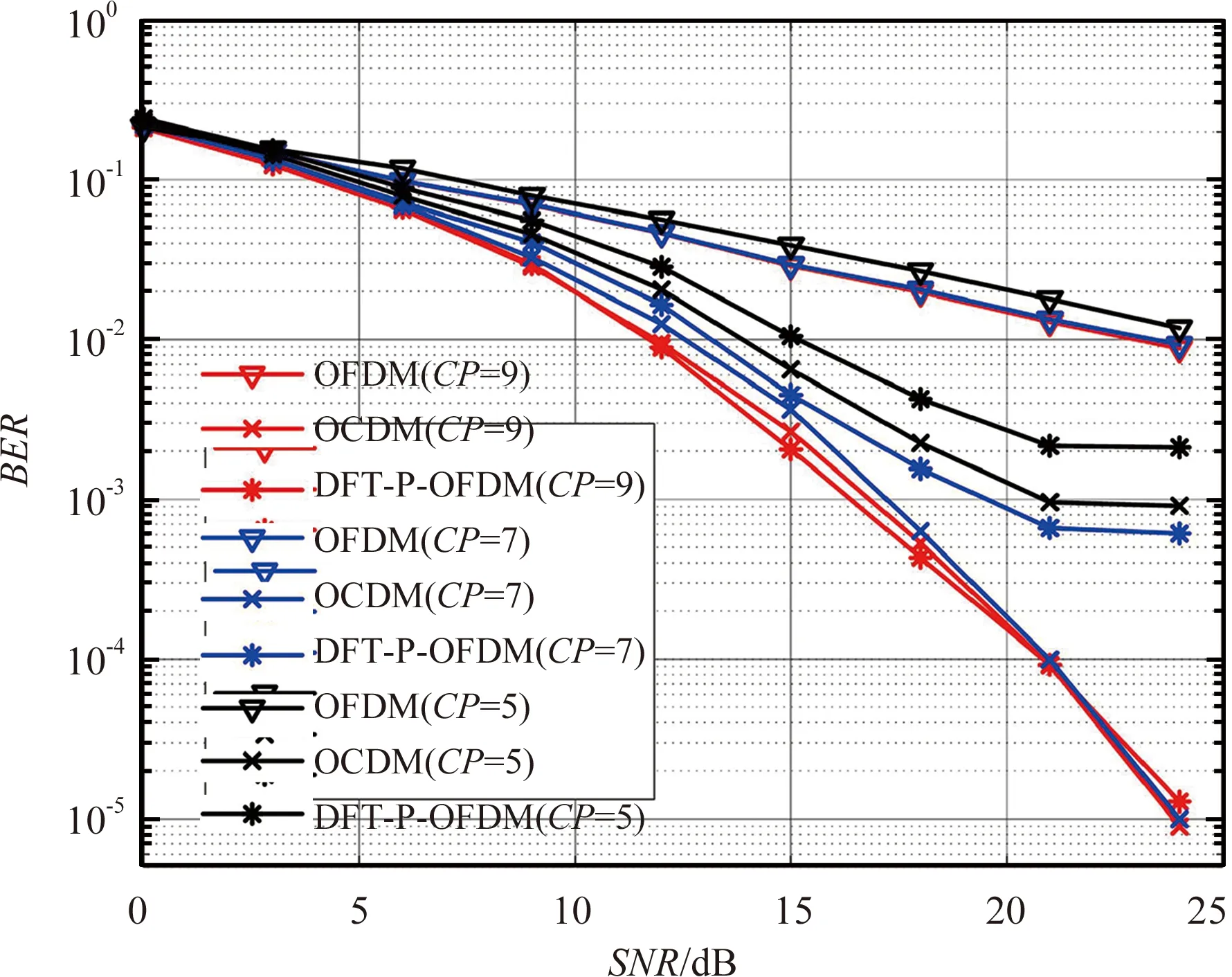
图7 针对CP长度的仿真结果图
相对于 DFT-Precoded-OFDM 系统,OCDM 系统和OFDM系统类似,采用了并行多载波的传输模式,符号在每个子载波上时域的持续时间得到了扩展,故其抗ISI的能力更强。而 DFT-Precoded-OFDM 系统本质上是一种单载波传输系统,不具备这种抗干扰能力,因而误码性能衰减更快。
5 结论
本文基于正交线性调频复用系统的数字实现原理详细研究了该系统在不同多径数目、多普勒频移以及循环前缀长度下误码性能并进行分析,仿真结果表明,OCDM系统并行传输的多个子载波都是宽带且相互正交。因此,其信息传输在时间、频率域都得到了充分的扩展而具备了更强的抗多径、抗多普勒扩展的效果。其有望在以水下通信为例的恶劣环境中成为宽带传输的一种更具鲁棒性的备选波形。
