基于集群的主动配电网双层分布式优化调度策略研究

詹成康，李晓露，陆一鸣，刘日亮 ，李聪利

（1.上海电力大学电气工程学院，上海 200090；2.国网上海能源互联网研究院有限公司，上海 200090；3.国家电网有限公司，北京 100031；4.国网天津市电力公司，天津 300010）

随着“源”侧分布式电源中以光伏、风电为主的可再生能源大规模接入主动配电网中，其新能源出力的间歇性和波动性给配电网的调度运行带来了挑战。同时，“荷”侧需求响应技术、温控负荷、电动汽车等可调节资源的不断推广，使得主动配电网呈现“源-荷”双向不确定的特点[1]。针对上述问题，若采用传统的集中调控方式，不仅通讯负担重，也难以对大规模分布式能源进行“可观可控”[2]。因此，需要研究计及分布式资源集群的主动配电网的分布式优化调度理论和方法[3]。通过对可再生分布式电源与可调节负荷资源集群进行灵活调控，有效地应对“源-荷”侧各种不确定性，实现主动配电网中各分布式单元的高效运行[4]。

近年来，基于“群内自治、群间协调”的分层分布式架构的配电网技术成为研究热点。一方面，对所有设备进行统一集中调度复杂程度较高，几乎无法实现，为此可以将集群内的分布式资源设备作为一个整体，对各个集群进行优化调度。另一方面，在分布式架构下，这些分布式资源可以在集群内整合，在一定程度上提供辅助服务，有效地参与电力市场的交易，促进新能源的消纳[5]。因此，需要研究主动配电网集群分布式优化调度的理论与方法。

主动配电网的分布式优化调度在国内外已有一定的研究[6]。文献[7]提出了基于一致性算法解决智能电网中的经济调度问题，通过运用一致性算法使得各分布式电源的增量成本趋于一致，满足“等耗量微增率原则”，从而获取经济调度问题的最优解。文献[8]基于一致性算法实现主动配电网的分布式优化调度，通过一致性迭代算法使各分布式电源增量成本趋于一致，实现主动配电网自治区域的发电成本优化。但是，上述文献仅仅考虑“源”侧的成本函数，没有计及可调节负荷资源。文献[9]提出了增量效益一致性算法用以解决含分布式电源和需求响应构成的智能电网中能量管理问题。文献[10]提出了计及“源-荷”综合效益的智能电网动态社会效益最大化模型，基于交替方向乘子分布式算法对智能电网的最优能量管理进行分布式优化。然而，这些传统分布式算法存在全局变量获取困难的问题。文献[11]提出了将一致性算法和调频控制结合以解决上述问题，但在算法设计的同时结合了控制因素，增加了其复杂性。文献[12-13]提出了“一致性+创新项”结构的一致性算法，通过创新项对功率平衡约束进行局部评估，但需增加智能体数量以获取全局变量信息。

实际上，由于主动配电网中含有大量的分布式资源，若在全局优化阶段对所有设备进行统一调度会极大地增加计算的复杂程度。因此，在全局优化阶段可将集群内的分布式资源进行聚合，通过“群控群调”以简化复杂程度。关于分布式资源的整合国内外也有相关的研究。文献[14]在日前调度阶段基于闵可夫斯基求和对需求侧可调节设备的备用容量进行求解，文献[15]基于闵可夫斯基求和对每个时刻功率刻画的奇诺多边体求解，从而实现灵活性功率的聚合与分解，文献[16]在此基础上对需求侧储能与灵活性负荷进行协调调度。然而，上述文献只是单一地对“荷”侧可调节资源进行整合，并未对“源-荷”分布式资源进行整合。

综上所述，现有的文献几乎没有对计及“源-荷”的分布式资源集群进行协调调度，同时也未综合考虑上层全局优化与下层局部优化调度。为了解决上述问题，本文提出了一种基于“源-荷”集群功率偏差的主动配电网双层分布式优化实时调度策略，以基于多智能体架构的主动配电网为研究对象[17]，在上层“群间协调”全局优化阶段，设置各智能体间“源-荷”集群功率偏差作为一致性变量，对各个智能体所管辖的集群进行分布式优化调度，在下层“群内自治”局部优化阶段，根据各分布式单元增量成本的迭代方程实现最优效益下的“源”侧出力与“荷”侧需求，实现集群内分布式资源的协调优化。

1 多智能体架构建模与问题描述

本文以基于多智能体架构的主动配电网为研究对象[17]，其结构如图1所示。每个智能体包含分布式光伏、风机、电动汽车、储能、可控负荷，可建立在含分布式灵活性资源的聚合商中。通过聚合商将这些分布式灵活性资源聚合成集群，在日内实时滚动优化阶段，每个智能体通过执行基于“源-荷”集群功率偏差的分布式优化实时调度策略，实现下层各分布式资源的协调优化。同时，各智能体可与邻近智能体进行有限的信息交互，通过改进的一致性算法，获得上层集群功率分担方案与动态经济调度最优解。

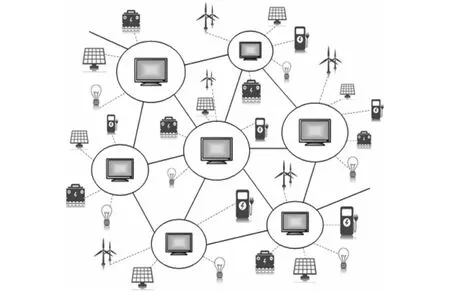
图1 多智能体架构下主动配电网集群Fig.1 Cluster of ADN based on multi-agent architecture

1.1 主动配电网“源-荷”协同能量管理优化问题

对于基于多智能体架构的主动配电网的能量管理系统，主动配电网“源-荷”侧动态能量管理的优化问题可以表述为

式中：Ci[PG,i(t)]为第i台分布式电源的成本函数，PG,i(t)为第i台分布式电源t时刻的输出功率；n为分布式电源的总数；Uj[PD,j(t)]为第j个用户效益函数，PD,j(t)为第j个用户t时刻消耗的功率；q为负荷用户总数；t为在动态能量管理优化问题中设置的时间间隔，t=1，2，…，T。

约束条件如下：

1）功率平衡约束方程：

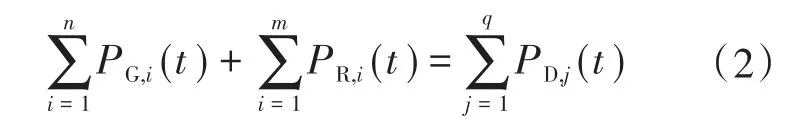
式中：PR,i(t)为第i台可再生分布式电源在t时刻的输出功率；m为分布式电源的总数。

2）“源”侧出力限制：

3）“源”侧爬坡约束：

4）“荷”侧用电功率限制：

1.2 主动配电网“源”侧成本建模

1）分布式电源。对于分布式电源提供能源输出的成本称为“源”侧的成本函数，一般由多段线性函数或二次函数估计表示。选用合适的成本函数对于充分预估分布式电源的性能表现和解决主动配电网能量管理问题具有重要意义。本文选取二次数学函数对传统分布式电源的成本进行建模[9]，其表达式为

式中：α，β，γ为每个分布式电源成本函数的系数。

2）可再生分布式电源。分布式电源过量出力可以衡量分布式电源所产生的效益。当能源的销售价格大于其生产能源所需的成本时，则第i台分布式电源的利润函数可以表示为

3）电动汽车。对于分布式资源中的电动汽车，其参与分布式优化调度中的电动汽车成本函数Ci[PEV,i(t)]可以用二次函数进行拟合，如下式：

1.3 主动配电网“荷”侧效益建模

1）灵活性可调节负荷。电力市场中需求侧的每个用户在一天的不同时间段内都有各自的用电偏好。聚合商可以收集用户侧的可调节负荷资源，通过与用户侧资源签订合同，运用价格激励引导和改善现有的负荷运行曲线，用户侧在改善用电习惯的同时获取一定的经济效益。本文选取二次函数以表达“荷”侧用户效益函数，其表达式为[9]

“荷”侧用户效益函数Uj(PD,j(t))是关于PD,j(t)的函数，其分别由成本参数b和收益参数ω决定。

2）储能单元。储能单元收益函数如下式：

式中：PBESS,j(t)第j个储能单元t时刻发出的功率；θj储能单元收益函数的系数。

2 基于一致性理论的分布式优化调度

2.1 分布式资源集群等值模型

本文以基于多智能体架构的主动配电网为研究对象，根据“群内自治、群间协调”的分层调控思想，实现“群控群调”的目的。其中，本文通过聚合商对分布式光伏、风机、可控负荷等“源-荷”侧资源进行聚合，通过对各智能体间进行协调优化，实现主动配电网分布式资源集群优化调度。

本文设计的各分布式能源资源（distributed energy resources，DERs）集群调控体系架构如图2所示。为了实现分布式资源集群对主动配电网提供灵活性可调节能量，首先应根据DERs地理位置、电网需求等对其进行集群划分，在“群内自治”阶段基于分布式一致性算法实现群内DERs单元自治，上层Agent在获取DERs集群等值模型的同时整合集群内DERs所能提供的可调节灵活性能量，通过对DERs集群分布式协调算法，实现DERs集群间的协调调度优化。

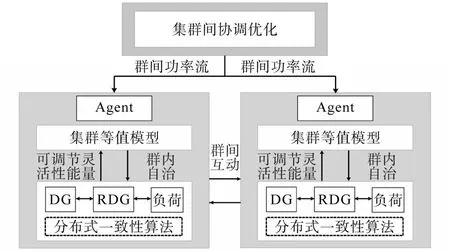
图2 DERs集群调控架构体系Fig.2 Distributed energy resources dispatch and control architecture system

分布式一致性算法在本质上讲，是指各智能体间通过信息的有限交互使得状态变量趋于一致。在上层“群间协调”全局优化阶段，令每个智能体管辖的集群中分布式资源“源-荷”集群功率偏差进行量测，并作为全局分布式优化调度的收敛判据，经过有限次迭代后，使得每个智能体所管辖的集群中“源-荷”集群功率实现平衡：

其中

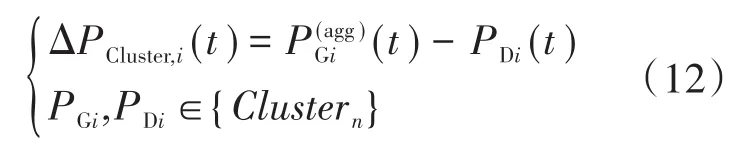
2.2 基于集群功率偏差的改进一致性算法

在多智能体架构下主动配电网集群中所管辖的分布式资源，结合1.1节中“源-荷”协同能量管理分析，实现各个集群中的分布式资源“源-荷”综合效益最优下“源”侧出力与“荷”侧需求。

其中

式中：λi，λj分别为第i，j个智能体的一致性变量；aij为拉普拉斯系数；ηi为调整误差系数；ϖij为智能体单元i与智能体单元j的权重系数；Pi(k)，

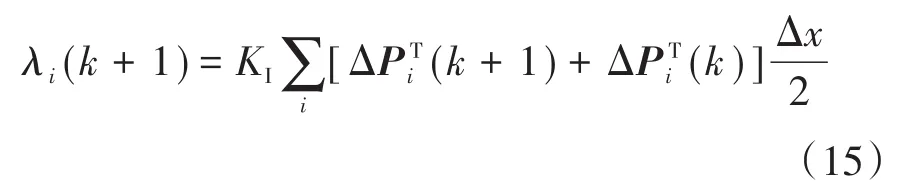
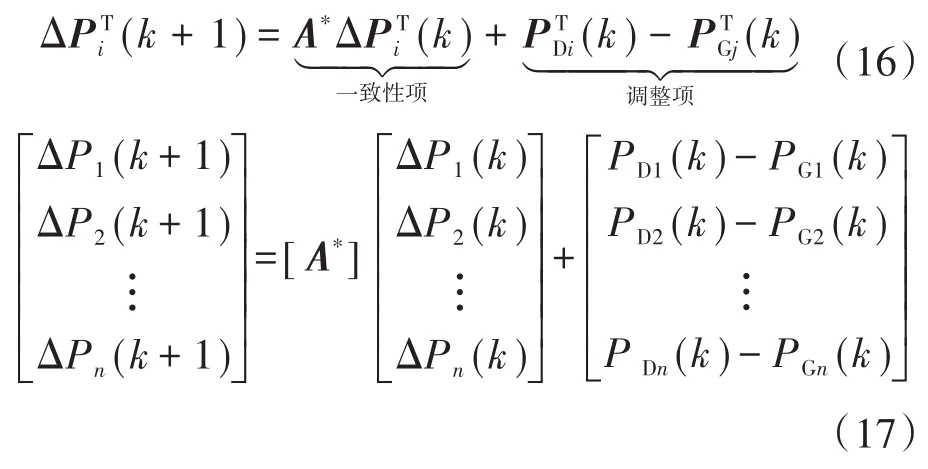
本文选取“源-荷”综合效益微增率ρ为一致性算法的状态变量，作为“一致项”，根据迭代算法ρ会向最优值逐渐逼近，但当不满足各种约束条件时，这个最优值并不一定是ρ*。因此还需加入“调整项”反馈修正令结果逼近ρ*。

为了规避上层调度部门对用户隐私信息参数的需求，本文定义“源-荷”集群功率偏差ΔP为各邻近智能体间交互的信息，此时各分布式能源微增率一致性变量的计算式为

需要注意的是，功率不平衡值ΔP是与邻近节点需要交互的唯一信息，并不需要包括用户的隐私信息，所以在邻近矩阵A*中，任何与用户侧相连的元素为都为零，更重要的是，用户只需和最多一个分布式电源建立通信通道，大大简化了通信的复杂度。而传统的分布式优化调度中邻近矩阵A*中与用户相连接的元素都不为零。因此，在本文所提的策略中，简化的邻近矩阵A*含有大量的零元素，可以大大简化计算的复杂程度。

在下层“群内自治”局部优化阶段，根据拉格朗日乘子与 KKT（Karush-Kuhn-Tucker）条件可知，在满足约束条件（式（2）～式（5））下，目标函数（式（1））获取最优解时满足“等微增率准则”，即各分布式单元微增率λ(k)相等时取得最优值。因此，“源-荷”综合效益最优下各分布式单元微增率满足下式：

根据微增率λ(k)可以求取“源”、“荷”侧分布式单元的出力情况。在第k次迭代下，“源”侧的输出功率表达式为

每个智能体的控制器可以根据已知的成本系数α，β以及计算得到的λG(k)，λD(k)，结合式（6）的“源”侧成本函数得到其输出功率。当求得“源”侧微增率λ(k)时，可以将其与同集群的负荷消费者进行信息共享，结合式（9）求得最具效益的“荷”侧需求功率：

为了便于总结，以表1的形式直观地将传统的基于一致性算法的分布式经济调度和本文所提的基于“源-荷”局部功率偏差的改进一致性算法进行比较。

表1 主动配电网分布式优化算法比较Tab.1 The compare of the ADN distributed dispatch algorithms

比较表1中归纳的方法可以看出，采用本文所提的基于“源-荷”局部功率偏差的改进一致性算法，在一致性变量计算的过程中可以有效地规避用户信息α，β，γ，ε，μi，b，ω，θj参数变量的需求，保护了隐私数据，同时也确保各个主体的公平竞争。

2.3 收敛性分析

为了验证本文设计的分布式双层优化调度中对“源-荷”集群功率偏差改进的合理性，本文对基于“源-荷”集群功率偏差的“一致性+调整项”分布式算法的收敛性进行证明，过程如下：

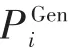
根据拉格朗日乘子与KKT条件可知，在下层局部优化中“源-荷”侧一致性变量相等时即可，此时可对式（21）化简为

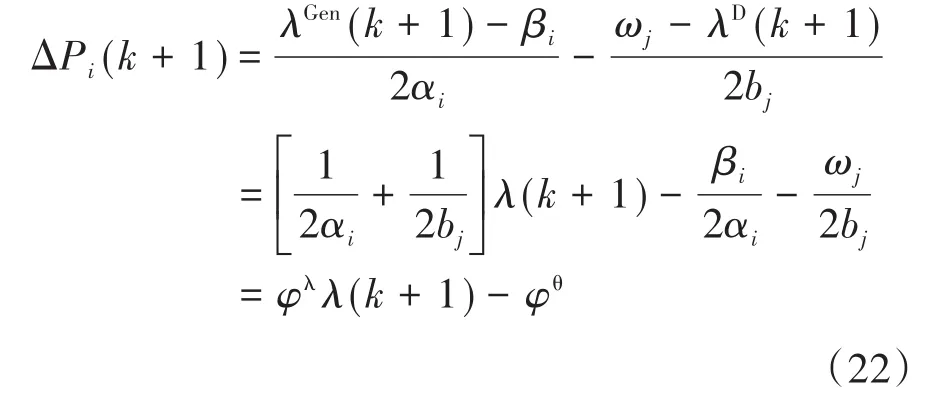
其中

当k=0-时，有：

当k=0时，有：

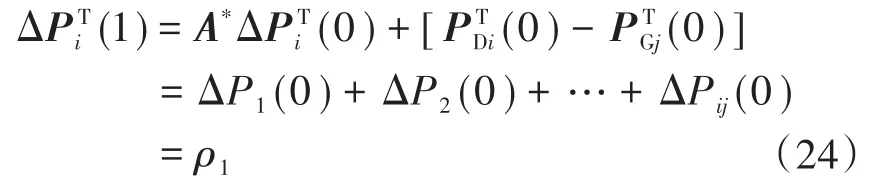
当k=1时，有：

结合式（15）分析，当k=0时有：

当k=1时有：

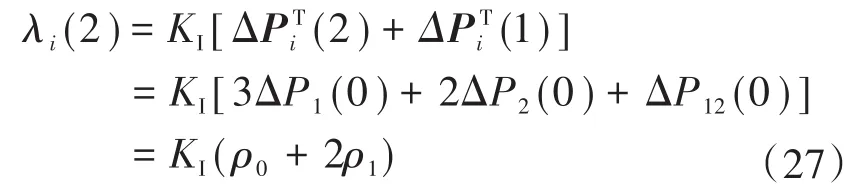
通过归纳类比可得第k+1此迭代下有：

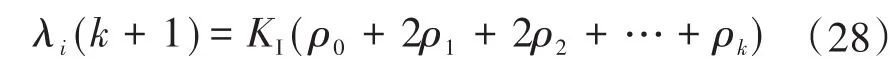
3 主动配电网双层分布式优化调度

针对主动配电网的分布式集群优化调度问题，本文提出了一种基于“源-荷”集群功率偏差的双层分布式优化调度策略。在上层“群间协调”全局优化阶段，各智能体对集群间进行协调调度以满足全局功率约束，通过设计的基于“源-荷”集群功率偏差的改进一致性算法，实现各智能体集群间的全局能量优化管理。在下层“群内自治”局部优化阶段，每个智能体对负责管辖的分布式资源进行协调优化，结合“源”侧成本函数与“荷”侧效益函数，当各分布式单元增量成本相等满足“等耗量微增率原则”时，获取最优效益下的“源”侧最优出力与“荷”侧最优负荷需求，实现智能体集群内的局部能量优化管理。在获取“源-荷”侧最优出力后，更新集群内功率偏差信息，并以此作为下一次算法迭代时上层全局优化阶段初始值，实现上、下层算法的交互。主动配电网的分布式资源集群双层优化调度策略如图3所示。

图3 主动配电网分布式双层优化调度策略流程图Fig.3 Flow chart of distributed two-level optimal dispatching strategy for ADN

步骤1：根据最初运行状态参数，计算各智能体集群功率偏差的初始值以及微增率一致性变量的初始值；

步骤2：以基于多智能体架构的主动配电网为研究对象，根据智能体所形成拓扑结构计算拉普拉斯矩阵；

步骤3：根据式（13）的迭代算法更新计算每个智能体的增量成本；

步骤4：根据式（18）、式（19）分别计算在最优效益下的“源”侧出力与“荷”侧需求；

步骤5：各智能体间根据式（15）进行分布式协调优化调度，计算新的集群功率偏差信息，当满足收敛判据时即可获得主动配电网分布式资源集群优化调度的最优解，当不满足收敛判据时，返回步骤3继续更新每个智能体的增量成本，继续执行图2算法流程直至满足收敛判据为止。

4 仿真分析

4.1 仿真系统说明

为了验证所提的基于“源-荷”集群功率偏差的分布式优化调度策略，本文在IEEE 33节点配网系统上进行验证。其中“源”侧成本函数的系数和“荷”侧效益函数的系数参考文献[9]的数据，本文定义Agent1负责管理集群1的分布式资源，包含“源”侧序号8，10与“荷”侧序号16，17，18，26；定义Agent2负责管理集群2的分布式资源，包含“源”侧序号9与“荷”侧序号15，19，20；定义Agent3负责管理集群3的分布式资源，包含“源”侧序号1，2与“荷”侧序号11，12，13，24，25；定义Agent4负责管理集群4的分布式资源，包含“源”侧序号3，4，5，6，7与“荷”侧序号14，21，22，23，27，28，29。各Agent间通信线路连接用虚线表示。

图4 IEEE 33节点仿真结构Fig.4 IEEE 33-bus system simulation structure

4.2 “源”侧波动测试

设置分布式电源在IEEE 33节点系统每隔10 min发生变化，进行“源”侧波动测试。对基于“源-荷”集群功率偏差的改进一致性算法进行求解，得到的上层“群间协调”全局优化和下层“群内自治”局部优化结果分别如图5和图6所示。

在上层“群间协调”全局优化阶段，各集群的最优功率分配结果如图5所示。从5a可以看出，每个智能体在“源”侧波动设置的瞬间，其所管辖的功率会发生短暂的波动，但是在迭代算法的计算下各智能体管辖的功率都会快速收敛并趋于一个稳定值，从而获得各智能体稳态下的最优功率分配方案。从图5b中“源-荷”集群功率偏差仿真结果可以看出，在上层“群间协调”全局优化阶段，在本文所提出的基于“源-荷”集群功率偏差改进一致性算法的计算下，各智能体所管辖的“源-荷”的集群内功率偏差最终都收敛一致为零，最终实现了每个智能体所管辖的集群内各分布式资源“源-荷”集群功率平衡。

图5 “源”侧波动下全局优化结果Fig.5 Result of global optimization under the disturbance from source side

图6为“群内自治”局部优化下的仿真测试结果。可以看出，在“源”侧最初发生波动时，各分布式单元的增量成本都各不相同，但是基于改进的一致性算法可以快速使得各分布式单元增量成本收敛一致，从而实现了“源-荷”最优效益下经济调度的求解。

图6 “源”侧波动下局部优化结果Fig.6 Result of local optimization under the disturbance from source side

4.3 “荷”侧波动测试

设置需求侧负荷在IEEE 33节点系统每隔10 min发生变化进行“荷”侧波动测试。与“源”侧波动类似，通过基于“源-荷”集群功率偏差的改进一致性算法对系统进行求解，得到上层全局优化结果和下层局部优化结果，其示意图分别为图7、图8所示。

从图7a可以看出，各智能体所管辖的集群在受到“荷”侧波动的情况下仍然可以迅速求解，得到各智能体的最优功率分配方案；同时，图7b中各智能体间通过邻近节点间信息的交互，实现各智能体的集群功率偏差为0，实现了各集群的分布式优化调度。

图7 “荷”侧波动全局优化结果Fig.7 Result of global optimization under the disturbance from load side

从图8看出，各分布式单元的增量成本仍然趋于一致，最终得到最优“源-荷”效益下的功率分配方案，证明所提的调度策略在负荷较大波动的情况下仍能使集群内部功率平衡。

图8 “荷”侧波动下层局部优化结果Fig.8 Result of local optimization under the disturbance from load side

4.4 “源-荷”双侧波动测试

在上述“源”、“荷”单侧波动测试的基础上，同时设置分布式电源与需求侧负荷每隔10 min发生变化，进行“源-荷”双侧波动测试。基于设计的“源-荷”集群功率偏差对IEEE 33节点系统进行验证，其仿真结果如图9、图10所示。

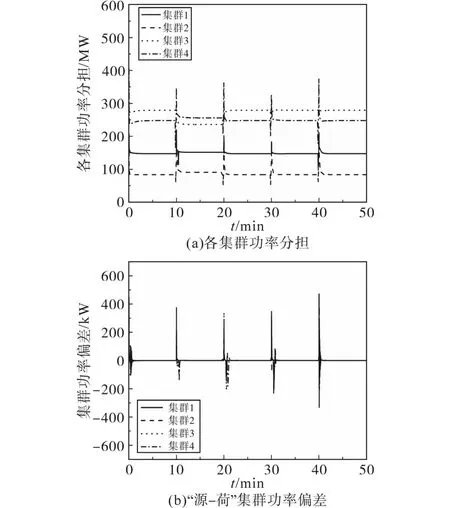
图9 “源-荷”波动下全局优化结果Fig.9 Result of global optimization under the disturbance from“source-load”side

从图9a中可以得出，尽管在每个时间段最初时刻同时有“源”侧波动与“荷”侧变化，但基于所提的改进一致性算法仍然可以求得各集群的最优功率分担。从图9b可以看出，各智能体所管辖的集群在受到“源-荷”侧双侧波动测试后，最终仍然可以实现各集群的“源-荷”动态功率平衡。

同时，从图10仿真结果图可以看出，各分布式单元的增量成本在经历“源-荷”双侧波动后依旧可以收敛一致，求得“源-荷”综合效益最优下增量成本的值。

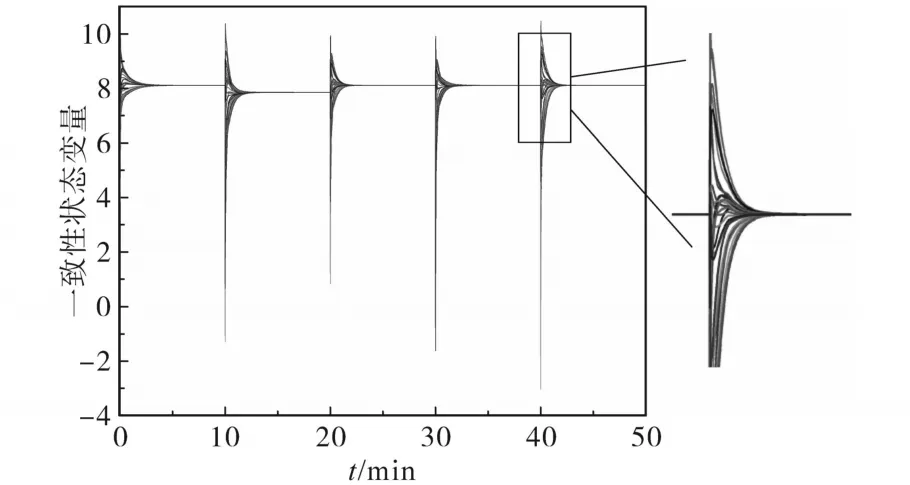
图10 “源-荷”侧波动下局部优化结果Fig.10 Result of local optimization under the disturbance from“source-load”side

由于本文所提策略的优点之一是可以大幅地简化邻近矩阵A的元素参数，提高计算效率。现将本文所提的基于“源-荷”集群功率偏差的分布式调度与传统的分布式优化调度进行比较，收敛时间如表2所示。

表2 计算时间比较Tab.2 Compare of the calculation efficiency

根据表2中信息可知，本文所提策略经过0.046 809 s完成收敛，而传统一致性算法下IEEE 33节点系统经过0.622 69 s完成收敛，可见本文所提基于“源-荷”集群功率偏差的分布式调度可以有效缩短计算时间。

5 结论

本文以基于多智能体架构的主动配电网架构为研究对象，根据“群间协调，群内自治”分层架构思想，提出基于“源-荷”集群功率偏差的双层分布式优化调度策，实现主动配电网分布式资源集群优化调度。得到如下结论：

1）在上层“群间协调”全局优化阶段，以集群功率偏差作为一致性变量，协调各智能体所管辖集群，获取最优功率分担方案求解，使各集群在受到波动后可以重新运行在新的功率稳定状态。

2）在下层“群内自治”局部优化阶段，以“源-荷”微增率为一致性状态变量，通过迭代算法实现了多种类型的分布式能源协调优化，充分发挥主动配电网中可调节灵活性资源的潜力。

3）为了缓解“源”侧可再生能源与“荷”侧新型负荷的各类不确定性，设计的“源-荷”分布式协调调度策略可以有效适应“源-荷”双侧的波动，同时可以获取“源-荷”综合效益最优下各集群功率分担并有效提高计算效率。

感谢孙明琦在本文修改过程中提出的宝贵意见！