基于三维空间墙体砌块的算量理论

刘春花，温志梅，李 红，郭仁东，胡记磊

(1.山东华宇工学院 能源与建筑工程学院，山东 德州 253034；2.三峡大学 土木与建筑工程学院，湖北 宜昌 443002)

在砖混结构的建筑物中，经常使用到标准砖砌块作为承重墙体和非承重墙体的主要建筑材料.由于墙体的厚度不同，单位体积内的用砖数量随墙体的厚度变化而变化.根据体积形状与用砖数量的关系可知，对于矩形体积三个维度方向的尺寸越互相接近，其单位体积(每立方米)内用砖数量越少.现有单位体积墙体砌块(标准砖)用量计算公式为[1-3]：

N=n/[C×(b+t)×(a+t)]

(1)

式中：N为用砖量，n为半墙厚的砖数，分别为1.0,2.0，3.0,…，t为灰缝厚度，a、b和C分别是砌块厚度、长度和墙厚.

本文将上述公式分母中墙体厚度换算为平均灰缝厚度与一个砌块厚度方向尺寸之和的计算方法，给出一个适用于各种不同厚度墙体单位体积用砖量的通用公式.使用公式对不同的墙厚进行砌块用量计算，给出不同墙厚砌块用量数值、极限墙体厚度的砌块用量值，以及不同墙体厚度砌块用量变化曲线.该公式的使用将减少砖混结构墙体工程量计算时间，降低劳动强度，改进计算软件算法[4].该公式还可以拓展为三维有限长度的精确砌块算量公式.使利用计算机软件计算任何实际墙体厚度、实际墙体高度、实际墙体长度的砌块，以及保温层砌块算量工程造价计算[5-6].

1 墙厚方向平均灰缝厚度概念

普通墙体一般为半砖厚c(计算厚度为标准砖宽度c′=c=115 mm)、一砖厚(厚度方向为标准砖长度b或两个砖宽度c加一个灰缝厚度t，c′=2c+t=b=240 mm)、以此类推，有一砖半厚、二砖厚等标准墙体厚度[7-9].一般将墙体三维方向设为墙的长度方向，即B方向；墙的宽度方向，即C方向；墙的高度方向，即A方向，如图1所示.假设砖墙在高度方向，即A方向为无限高度，可近似认为每块砖计算高度尺寸为a+t.砖墙在长度方向，即B方向也为无限长，可近似认为每块砖计算长度尺寸为b+t.砖墙在宽度方向，即C方向(如图1所示)为有限长.由此，可以定义此种墙体模式为一维有限厚度墙体.

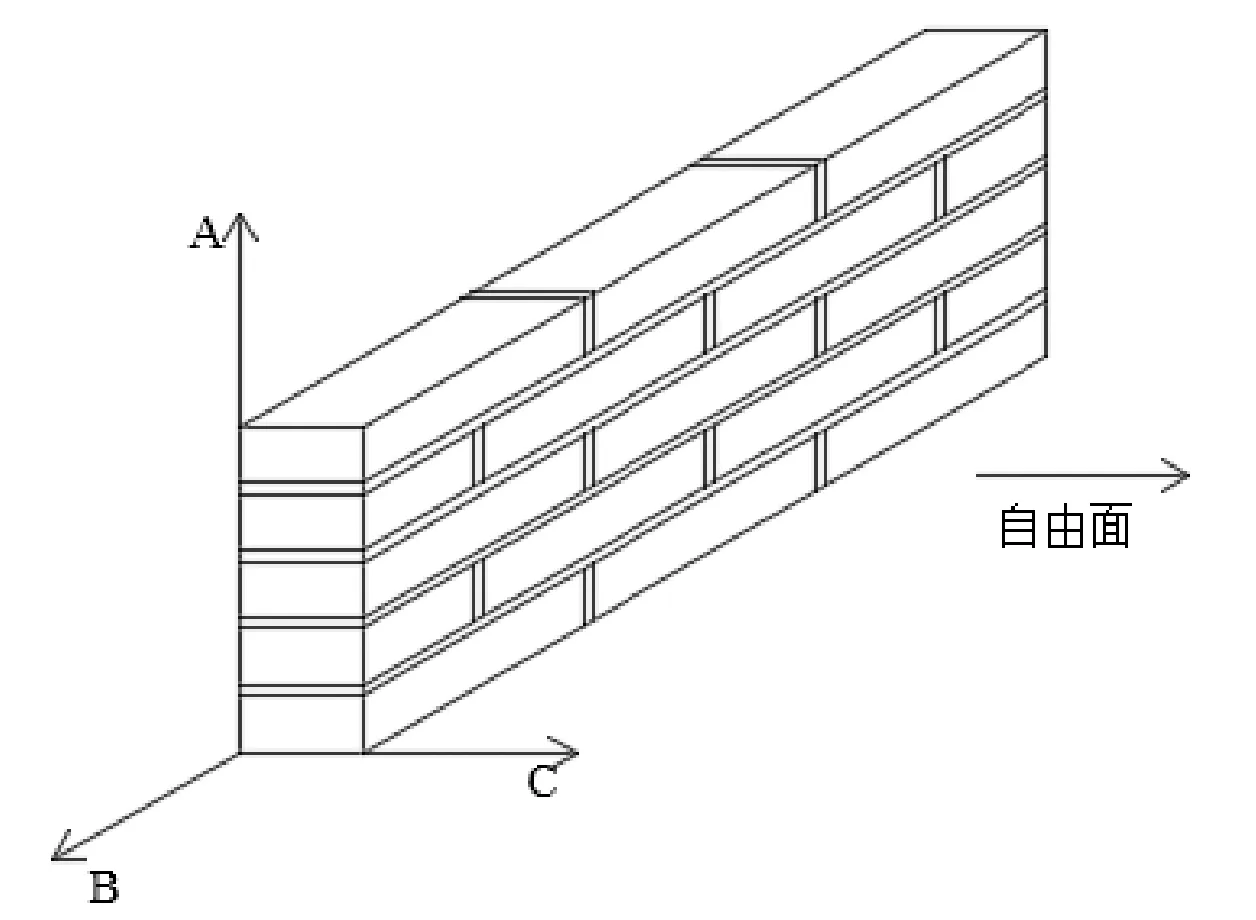
图1 标准砌块三维方向示意图

砌块厚度方向，又称自由面方向，即C方向.墙体的两侧为墙体的外侧，称之为自由面.在此方向，建立了平均灰缝厚度概念.平均灰缝厚度t′随半砖数n的增加趋近于灰缝实际厚度t.例如，对于半砖厚的墙体，即n等于1，厚度C方向墙体厚度等于c，得平均灰缝厚度t′=0.

三维有限厚度如图2所示，在宽度方向为两个半砖时，即每半砖含平均灰缝计算厚度为实际一个灰缝厚度的一半.当墙厚C方向为一砖半厚墙体时，即三个半砖平均分配两个灰缝厚度作为每块砖带有的平均灰缝厚度，以此类推，可见灰缝数永远比砖数少一个.根据数学归纳法理论，可以建立平均每块砖带有的平均灰缝厚度t′与实际灰缝厚度t、半砖块数n的数学模式如下

图2 标准砌块尺寸与砌筑墙厚示意图

c′=c+t′

(2)

(3)

式中：c′为一维有限墙厚方向单个砌块的计算厚度，c为一维有限墙厚方向单个砌块的实际厚度，t′为一维有限墙厚方向单个砌块的计算厚度所包含的平均灰缝厚度，n为墙厚方向半砖个数.

2 砌块墙体工程量计算公式

对于以上所述分析，可以建立三维变化墙体砌块算量的通用计算公式.设单位体积(1立方米)所含有标准砌块砖的数量为N，三维方向带灰缝单元砌块体积尺寸：高度方向(无限高)尺寸a+t，长度方向(无限长)尺寸b+t，只有宽度方向墙厚为有变化的一维(有限宽)尺寸c+t′.带灰缝单元砌块体积V=(a+t)(b+t)(c+t′)，用单位体积1立方米除以单元体积V可得该单位体积砌块数计算通用公式如下：

N=1/[(a+t)·(b+t)·(c+t′)]

(4)

或

N=1/[(a+t)·(b+t)·(c+t-t/n)]

(5)

式中：N为不同墙厚每立方米墙体所用砖数，a=0.053 m为砌块厚度(高度方向)，b=0.24 m为砌块长度，c=0.115 m为砌块宽度，t=0.01m为灰缝砂浆厚度，n=1,2,3,…为砖墙宽度方向的半砖数，如图2所示.

3 砌块算量通用公式特性分析

对公式(5)中单位体积砌块数N对墙体宽度半砖数变量n取极限，即n趋近于无穷大时，有：

(6)

式(6)为三维无限长墙体的单位体积砌块数的极限公式，该公式所得数据为所有三维有限长度墙体中用砖量最小值.对于标准砖砌块，将a=0.053 m,b=0.240 m,c=0.115 m,t=0.01 m代入公式(6)得单位体积最小用砖量为Nmin=507.94.这里需要注意的是，一般累加工程总用砖量时，最后计算的用砖量需要取整数.将其代入不同墙厚砖数n的公式(5)得相应的标准砌块砖数，如表1所示.

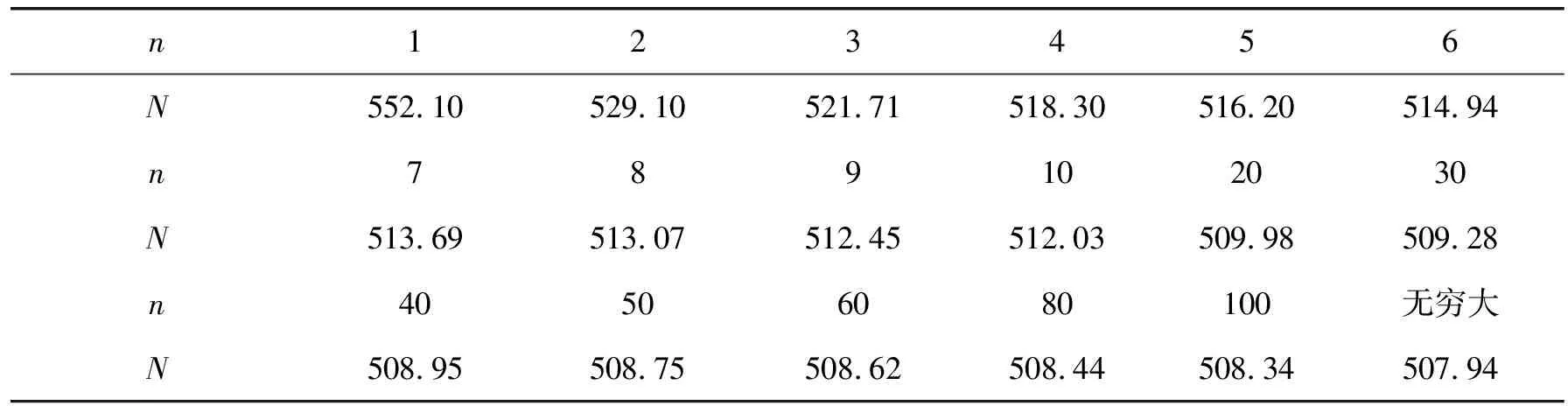
表1 标准砖墙厚度与用砖量

将表1中数据绘制成曲线，如图3示，可以看出砌块数N随着墙厚数n的增加而减少.

图3 墙体厚度与砌块用量变化曲线

4 结语

本文引入平均灰缝厚度概念及计算方法，使墙体砌块计算公式通用化，系统化，使普通施工与工程造价技术人员对算量公式的理解更加透彻，使用起来更加主动.并且引入维度概念，将墙体砌块计算公式建立为三维空间体系中墙厚方向为有限墙体砌块计算公式.平均灰缝厚度随墙厚的增加而趋近于实际灰缝厚度.单位体积砌块数量随维度增长(墙厚增大)而减少直至达到墙体为无限厚时的极限值.这种极限分析理论可以为三个维度方向都是有限墙体砌块的精确计算公式与现有公式计算公式对比，进行误差分析奠定理论基础.