跨越认知断层 走向深度学习——“三角形的面积”教学实践与思考

浙江省温州市滨江外国语小学 林志辉

浙江省温州市百里路小学 朱昭伟

【教学内容】

人教版数学五年级上册P95-96。

【缘起】

“三角形的面积”作为人教版数学五年级上册《多边形的面积》单元“平行四边形的面积”之后的内容，是在学生掌握了三角形的特征及长方形、正方形、平行四边形的面积计算的基础上进行教学的，同时又是进一步学习梯形面积、圆的面积和立体图形表面积的基础，是小学阶段“图形与几何”领域不可或缺的重要内容。概览国内人教、北师大、苏教等几个版本的教材，我们可以发现有些版本的教材同时采用割补法、倍拼法转化推导三角形的面积公式，所有版本的教材都采用了倍拼法转化推导三角形的面积公式。可见，教材对于面积转化推导过程及倍拼法的重视程度。

那么，学生是否具备转化推导三角形的面积的知识及经验基础呢？学生能否自行领悟“倍拼法”转化推导三角形的面积呢？在本课之前，学生已经经历了运用数格子等方法抽象概括长方形、正方形面积公式的过程，而在学习平行四边形的面积中，又初步掌握了运用转化思想和割补方法推导平行四边形面积公式的方法，为三角形面积公式推导奠定了一定的基础。具体到“倍拼法”，虽然学生之前学习过倍拼内容，但采用“倍拼法”进行面积转化，却是在本课第一次出现。通过前测，我们也发现，虽然大部分学生能用“数格子”“割补法”或直接运用面积公式求出格子图中的三角形的面积，但近80%的学生对于公式的推导过程并未真正理解。另外，尽管相对于“等积转化”，运用“倍积转化”推导三角形面积公式更加形象直观，却只有16%的学生想到用“倍拼法”进行面积转化。

那么，本节课如何带领学生经历三角形面积探索的全过程，跨越“等积转化”到“倍积转化”的认知断层，积累活动经验，发展空间观念呢？我们的想法是以核心大问题为引领，以关键问题为驱动，在图式相融、方法勾连中，跨越认知断层，进而实现三角形面积的深度学习。其教学目标确定为：

1.理解并掌握三角形面积转化的方法及面积公式，能正确计算三角形的面积。

2.经历三角形面积的探索过程，积累活动经验，进一步感悟转化的思想和方法，发展空间观念和初步的推理能力。

3.感受数学知识间的联系，收获学习成功的体验，激发数学学习的兴趣。

【教学实录】

一、“前测”对比，初感转化

（一）问题引领

师：这是一个平行四边形（见图1），它的面积是多少？如果在它里面画一个面积最大的三角形，三角形的面积是多少？

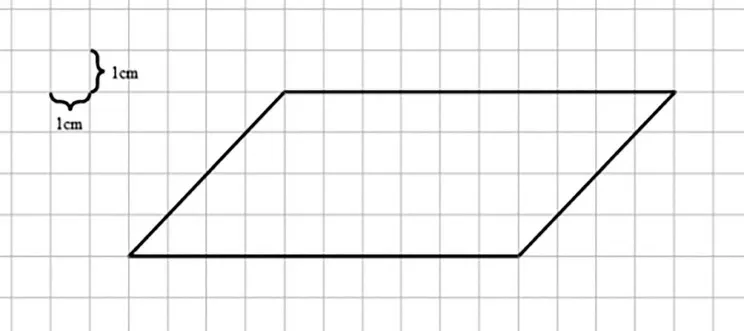
图1

（二）“前测”对比

1.反馈前测

师：其实，对于这个问题，课前我们已经做过研究。有的同学认为这个三角形（见图2）的面积是最大的，它的面积怎么计算？

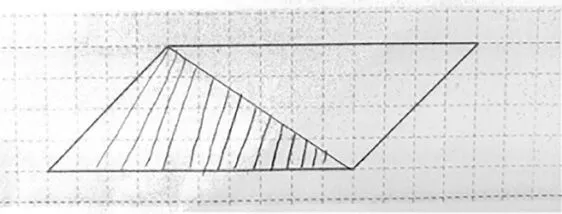
图2

生：此时把平行四边形分成两个一样大的三角形，所以，三角形的面积是平行四边形面积的一半，可以列式“10×4÷2”，它的面积就是20 cm2。

师：有同学列了同样的算式，但是他画的三角形却不一样，想象一下，可能是怎样的？

（学生思考想象，教师出示学生预学作品，见图3）

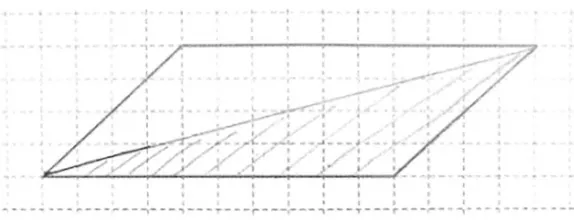
图3

2.对比聚焦

师：这两个三角形形状不同，为什么都可以用“10×4÷2”求面积呢？

生：因为它们都是同一个平行四边形面积的一半，所以都可以先算平行四边形的面积，再除以2。

师：都是同一个平行四边形的一半，平行四边形在哪里？

（课件出示平行四边形）

师（追问）：为什么求它们的面积都要除以2？

【设计意图：课前预学以“在平行四边形内画一个面积最大的三角形，并说明怎样计算它的面积”这样富有挑战性的问题激活学生的已有经验。在课始阶段以普遍性作品反馈、对比，勾连三角形和平行四边形的面积，引导学生在图式转化中初感三角形的面积转化。】

二、自主探索，再感转化

（一）自主探索

师：有的同学认为此时三角形的面积也是最大的，怎么计算它的面积呢？（见图4）

图4

师：想一想、画一画、算一算，在学习单（1）上表示出你的想法。

（学生自主探索，教师巡视）

（二）作品反馈

教师巡视并收集学生的代表性作品，反馈学生的作品：

1.割补法

作品一（见图5）：

图5

师：这是A同学的作品，你是怎么想的？

生：我是把三角形两边的部分通过割补，转化成一个长方形，长方形的长是三角形底边的一半，就是5cm，宽等于三角形的高是4cm，长方形的面积是5×4=20（cm2），长方形的面积等于三角形的面积，所以三角形的面积是20cm2。

作品二（见图6）：

图6

师：这是B同学列的算式：10×2=20（cm2） 。猜猜看，他是怎么想的？

生：把三角形上面部分进行分割，再通过割补转化成一个长方形，长方形的长是10cm，宽是三角形高的一半也就是2cm，长方形的面积是10×（4÷2）=20（cm2），长方形的面积等于三角形的面积，所以三角形的面积是20cm2。

作品三（见图7）：

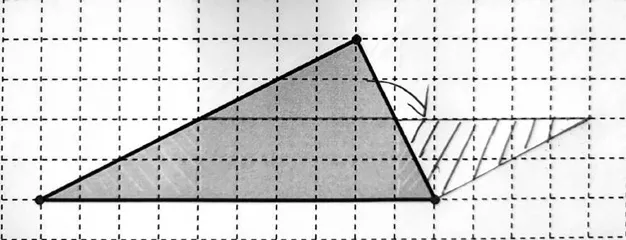
图7

师：刚才把三角形转化成面积相等的长方形求出它的面积。那么，这名同学又是怎么转化并计算面积的？

2.倍拼法

师：这个作品（见图8），你们明白他的想法吗？

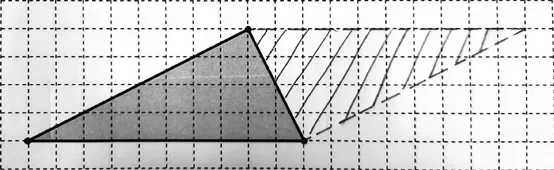
图8

生：我用两个一样的三角形，拼成一个平行四边形，这时平行四边形的长就是三角形的底等于10cm，平行四边形的宽就是三角形的高等于4cm，平行四边形的面积就是三角形面积的2倍，我先求出平行四边形的面积，再除以2，所以三角形的面积是10×4÷2=20（cm2）。

3.小结优化

（1）课件演示（见图9）

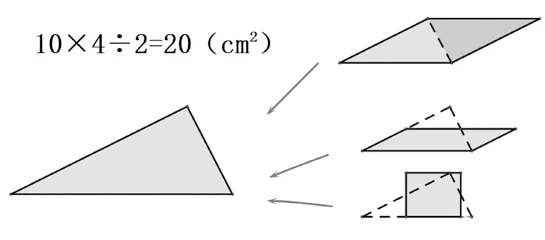
图9

（2）对比优化

师：这些方法都能推导求出三角形的面积，都可以转化成“10×4÷2”求出面积，这里的“÷2”是什么意思？

生：这里的“÷2”表示两个同样的三角形拼成一个平行四边形，平行四边形的面积是三角形的2倍，先求出平行四边形的面积，除以2就是三角形的面积了。

【设计意图：此环节让学生充分地自主探索，选取有代表性的作品多层次展示交流，由图到式、由式想图不断进行图式想象勾连，发展空间观念。在不同方法对比勾连中引导学生感知三角形面积的转化，逐步明晰倍拼法的优越性。】

三、推广归纳，完善转化

（一）由式想图，渗透等底等高

师：回看这个平行四边形（见图10），你还可以画出哪些三角形用这个算式计算面积？

图10

（课件拉动三角形的顶点，形成新的三角形，见图11）

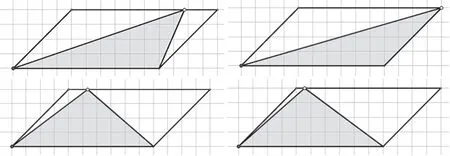
图11

师：为什么都可以用这道算式计算？

生：底都是10cm，高都是4cm，三角形的面积就都是10×4÷2=20（cm2）。

【设计意图：利用几何画板技术，在变化中寻找不变之处，既有想象和课件直观感受关键因素，又有抽象理性叩问。】

（二）推广归纳，得到面积公式

师：现在你能写出三角形的面积计算公式吗？

生：三角形的面积公式=底×高÷2。

师：是不是所有的三角形都可以这样求面积？

（学生想象，任意拉动三角形，再倍拼验证）

师：为什么都可以用底×高÷2来求面积？

生：因为不论三角形长什么形状，都能找到一个和它形状一样的三角形拼成平行四边形，平行四边形的面积是底×高，所以三角形的面积=底×高÷2。

师：转化前后的三角形和平行四边形有什么关系？

生：三角形的底是平行四边形的底，三角形的高是平行四边形的高，平行四边形的面积是三角形面积的2倍。

师：现在我们能明确三角形的面积=底×高÷2。

【设计意图：“是不是所有的三角形的面积都可以用底×高÷2表示？”“为什么都可以用底×高÷2来求面积？”“转化前后的三角形和平行四边形有什么关系？”问题串不断叩问，结合几何画板直观展示，促使学生思维更清晰、更深入、更全面、更合理。】

四、融会贯通，拓展延伸

（一）反思推理

反思1：为什么最大？

师：再来看这个问题，现在你能说明为什么此时三角形的面积最大了吗？（见图12）

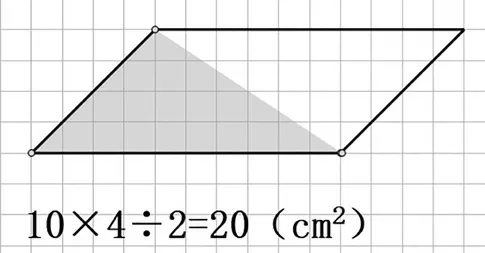
图12

生：三角形的面积是平行四边形的一半，平行四边形的面积是40 （cm2），三角形的面积最大只有20（cm2）。

生：要使面积最大，那么底要最大，高最大。此时底和高已经是最大的了，所以面积也就最大了。

反思2：还是最大吗？

师：此时三角形的面积还是平行四边形里最大的吗？（见图13）

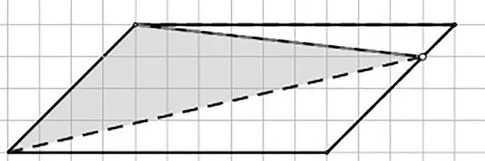
图13

师：现在你怎么想？（见图14）

图14

生：这两个三角形的底相等，高相等，面积肯定也相等，肯定也是最大的20cm2。

（二）延伸拓展

1.在梯形ABCD中画一个面积最大的三角形，面积是多少？（见图15）

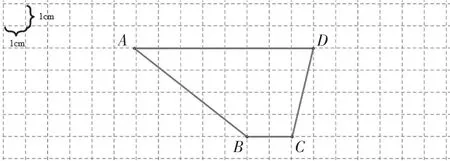
图15

2.图中有几对面积相等的三角形？面积是多少？（见图16）

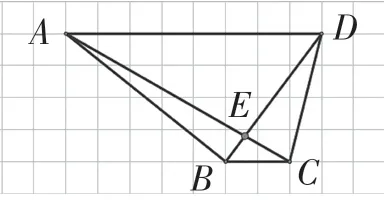
图16

【设计意图：此环节紧扣核心问题，一脉相承，首尾呼应，既有反思推理，又有公式灵活运用。练习开放且富有层次性，既是对本课的拓展练习，又有对三角形面积和梯形面积的勾连。】

五、课堂小结

（略）

【反思】

正如前文提到的，学生在“等积转化”和“倍积转化”间存在着认知断层。同时，本课又是在平行四边形面积推导基础上进一步加深对转化思想的感悟，在首次领悟“倍积转化”的同时完成对多种转化推导的融会贯通。本节课，我们尝试以核心问题为引领，跨越认知断层，以关键问题为驱动，带领学生经历转化、推导的全过程，实现三角形面积的深度学习。

（一）核心问题引领，跨越认知断层

本节课从前测开始，始终围绕核心问题（在平行四边形中画一个面积最大的三角形，并说明如何计算三角形的面积）进行引领教学。课前预学孕伏，大部分学生想到了平行四边形对角分割成三角形的情况，说明学生在问题解决中能自然把三角形和平行四边形进行勾连。课中有层次交流碰撞：“对角线分割作品对比异同”“非对角线作品自主探索”“等底等高三角形理性叩问”“面积最大三角形反思推理”“梯形中最大三角形延伸”。全课一脉相承，在核心问题的引领下，跨越认知断层，从“知其然”走向“知其所以然”，从而进一步尝试走向“知何由以知其所以然”。

（二）关键问题驱动，亲历转化全程

“这个三角形的面积怎么计算？”“为什么求它们的面积都要除以2？”“这里的‘÷2’是什么意思？你最喜欢哪种方法？”“是不是所有的三角形都可以这样求面积？”“为什么都可以用‘底×高÷2’来求面积？”“转化前后的三角形和平行四边形有什么关系？”“为什么此时三角形的面积最大？”回溯全课，我们不难发现本课在核心问题引领的同时，不断以关键问题驱动教学。学生纵向亲历从特殊到一般、从感性直觉到理性分析、从“具象”到“表象”到“抽象”的三角形面积转化推导的全过程，横向感悟了“割补等积”“双拼倍拼”等不同方法间的融通勾连，不断将思维引向更清晰、更深入、更全面、更合理。