建筑小区尺度下径流控制率与非点源污染负荷削减率协同关系研究
2023-02-04栾广学侯精明李东来杜颖恩王洁瑜
栾广学,侯精明,马 鑫,李东来,杨 露,杜颖恩,王洁瑜,刘 园
(1.西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048;2.中国电建集团西北勘测设计研究院有限公司,陕西 西安 710065)
城市非点源污染是指城市地表污染物在降雨径流的淋溶冲刷作用下以分散、广域的形式进入河湖引发的水体污染[1]。降雨是城市非点源污染形成的动力因素,而降雨形成的径流是非点源污染物迁移的载体。因此,狭义上的城市非点源污染即城市降雨径流污染,它是城市非点源污染的最主要形式[2]。
国外城市非点源污染研究起步较早[3],很多国家在20世纪70年代就对城市地表径流开展了大量测试及研究[4-5]。目前,我国城市化比例不断增加,市区不透水面积比例不断增大,导致降雨径流量增加,城市非点源污染问题日渐突出[6-9]。利用模型进行水文水质模拟是研究城市暴雨径流污染管理和控制的重要手段[1-2,10]。暴雨洪水管理模型(Storm Water Management Model,SWMM)采用一系列可以对参数进行校核的经验方程对非点源污染的发生、迁移及排放过程进行动态模拟[11-12]。我国很多学者也基于SWMM对城市非点源污染开展了研究[13]:李立青等[14]研究了两场降雨时间间隔对城市非点源污染负荷的影响;蒋春博等[15]研究了雨水花园对降雨径流的影响,并认为径流控制率与污染负荷削减率具有很高的相关关系;马晓宇等[16]研究了不同重现期对城市非点源负荷的影响;陈莎等[17]研究了低影响开发(low impact development,LID)措施对城市雨水径流污染的影响。相对而言,针对不同降雨条件下径流控制率与污染负荷削减率的定量协同关系的研究并不多[18]。因此,本文设计了不同重现期和雨峰系数的降雨条件,基于SWMM研究了径流控制率与污染负荷削减率的协同关系,以期为城市非点源污染研究提供参考。
1 研究区概况与数据来源
天福和园小区[19]位于陕西省西安市西咸新区,东靠丰信路,西邻沣西新城咸户路,南连公园大街,北接尚雅路。多年平均降水量为520 mm[20],降水多集中在汛期7—9月,且夏季发生暴雨的频率较高,易引发内涝。小区占地面积约3.67 hm2,小区内布设有雨水花园和透水铺装两种LID措施,分别占小区总面积的7.92%和14.34%。管网数据和下垫面数据由CAD图纸获取,降雨数据为气象站实测降雨数据,水文模型数据通过率定得到,水质模型数据根据SWMM用户手册及参考相近地区水质模型参数得到。西安城区短历时暴雨集中,以单峰型居多,因此,选用芝加哥雨型作为设计降雨,暴雨强度公式[21]为
(1)
式中:q为降水强度,L/(s•hm2);P为重现期,a;t为暴雨历时,min。
为增加模拟结果的可信度,本文选取9种重现期及5种不同雨峰系数条件下共45场降雨的模拟结果对小区尺度径流控制率与非点源污染负荷削减率的协同关系进行分析,重现期分别取1 a、2 a、3 a、5 a、10 a、20 a、30 a、50 a和100 a,雨峰系数r分别取0.20、0.35、0.50、0.65和0.80,暴雨历时均采用120 min,时间步长为5 min。不同重现期和雨峰系数下的设计降雨如图1所示。
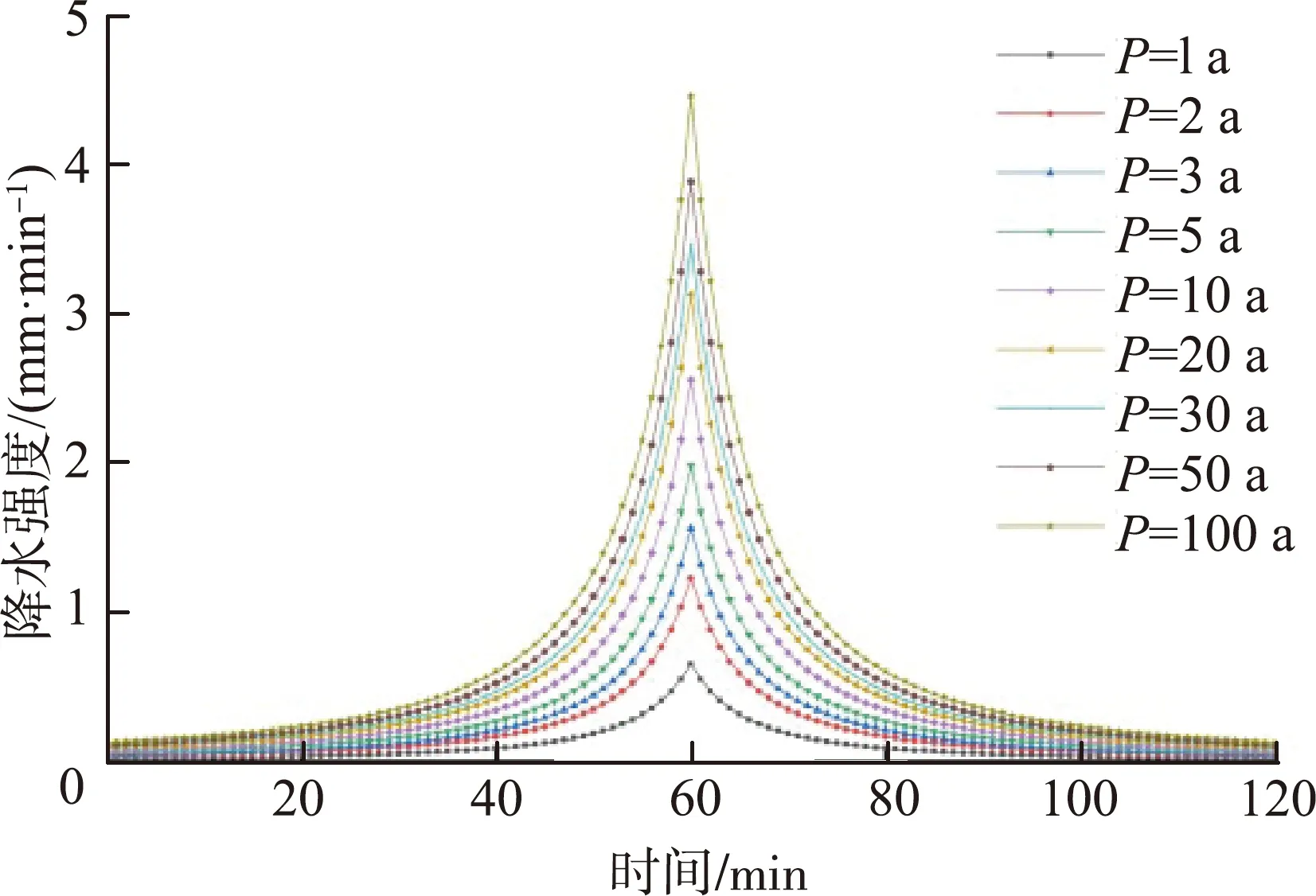
(a) 不同重现期

(b) 不同雨峰系数图1 不同重现期和雨峰系数的设计降雨Fig.1 Design rainfall with different return periods and rainfall peak coefficients
2 研究方法
2.1 数值模型
SWMM是美国环保署开发的一款动态降雨径流模拟软件[22]。模型可对不同设计降雨条件下的水量和水质进行模拟、预测和评估[23]。因为SWMM具有界面友好、开源获取、建模简便和管网模拟功能强大等优点[24],本文选用SWMM软件对降雨径流进行模拟研究,模型包括水文水动力模块和水质模块[22,25]。
水文水动力模块包括地表产汇流及管道汇流模拟[26]。SWMM将研究区域划分为多个子汇水区,地表产流和汇流过程计算分别在相应子汇水区内进行[27]。子汇水区由3部分组成,分别为透水区、无洼蓄的不透水区和有洼蓄的不透水区[28]。SWMM的产流模拟方法包括霍顿(Horton)公式法、格林-安普特(Green-Ampt)公式法等,其中Horton公式法比较适合于城市地区[19],故本文采用Horton公式法。采用非线性水库法对汇流过程进行计算[29]。SWMM的管道汇流模拟提供了恒定流、运动波、动力波3种计算方法[30]。恒定流法和运动波法是简化方法,计算效率较高但应用效果一般,动力波法基于完整的一维圣维南流量方程求解[24,31],应用效果最好,故本文采用动力波法。
水质模块根据功能区或土地利用类型定义各种地表污染物的冲刷模型和累积模型,对地表径流中污染物的增长、冲刷、运输和处理过程进行模拟[1]。本文采用指数函数冲刷模型和饱和函数累积模型。选用TN、TSS、TP、COD这4个具有代表性的雨水径流污染指标作为模拟对象[32]。
流量计布设于西南排口处,以获取排口处流量过程。模型首先将研究区划分成若干个子汇水分区,对管网进行概化,再根据实际地形选择合适的流向,经产汇流过程及管网汇流过程,最后在出口处进行模拟监测[33]。根据管网资料[21]、LID措施布置图及实际地形构建SWMM,将研究区域划分为绿地、道路、房屋3种土地利用类型[34],面积占比分别为39.89%、22.77%和15.09%。模型共有71个子汇水分区、31段雨水管网、31个节点和1个排口。研究区域概化图如图2所示。
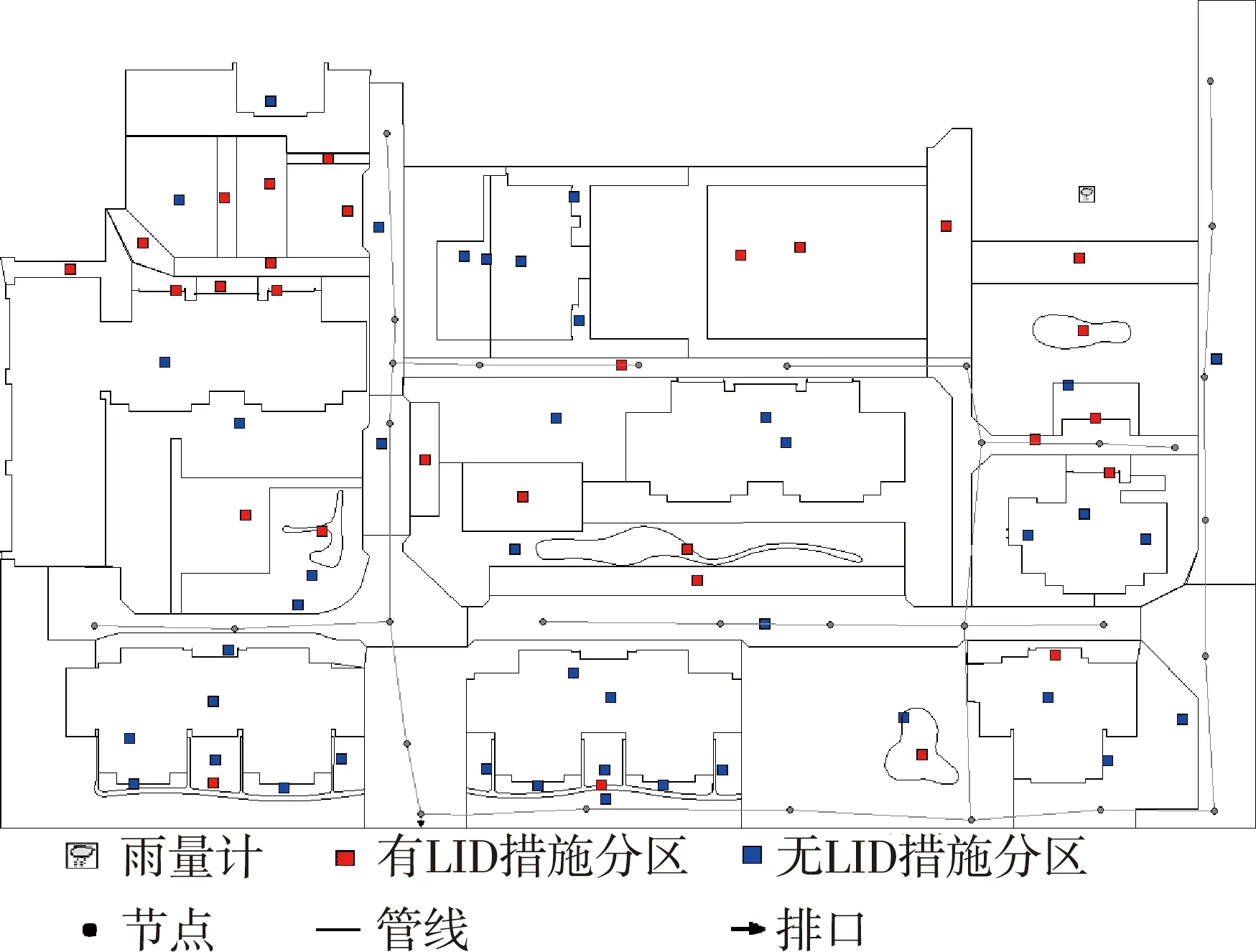
图2 研究区域概化Fig.2 Generalized map of study area
2.2 参数率定与模型验证
模型验证数据来自小区内自动雨量站的实测降雨数据和相同时段内西南排口的实测流量数据。雨水水质模拟通常依赖并伴随着水量模拟,只有水量得到正确模拟,才能保证水质预测的可靠性。根据沣西新城2017年8月20日和9月9日两场实测降雨径流数据率定水文水动力参数,表1为主要参数的率定结果,模拟数据与实测数据对比见图3。研究区域空间变化较小,总面积不大,故设定0.5%为各子汇水分区的平均坡度,相同属性下垫面参数设置一致[18]。
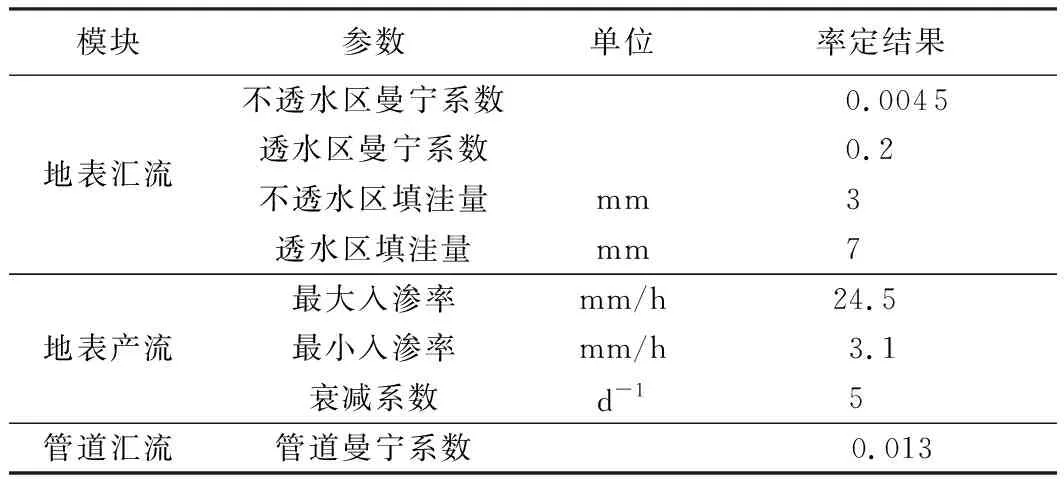
表1 模型水文水动力参数率定结果Table 1 Calibrated redults of model hydrodynamic parameters

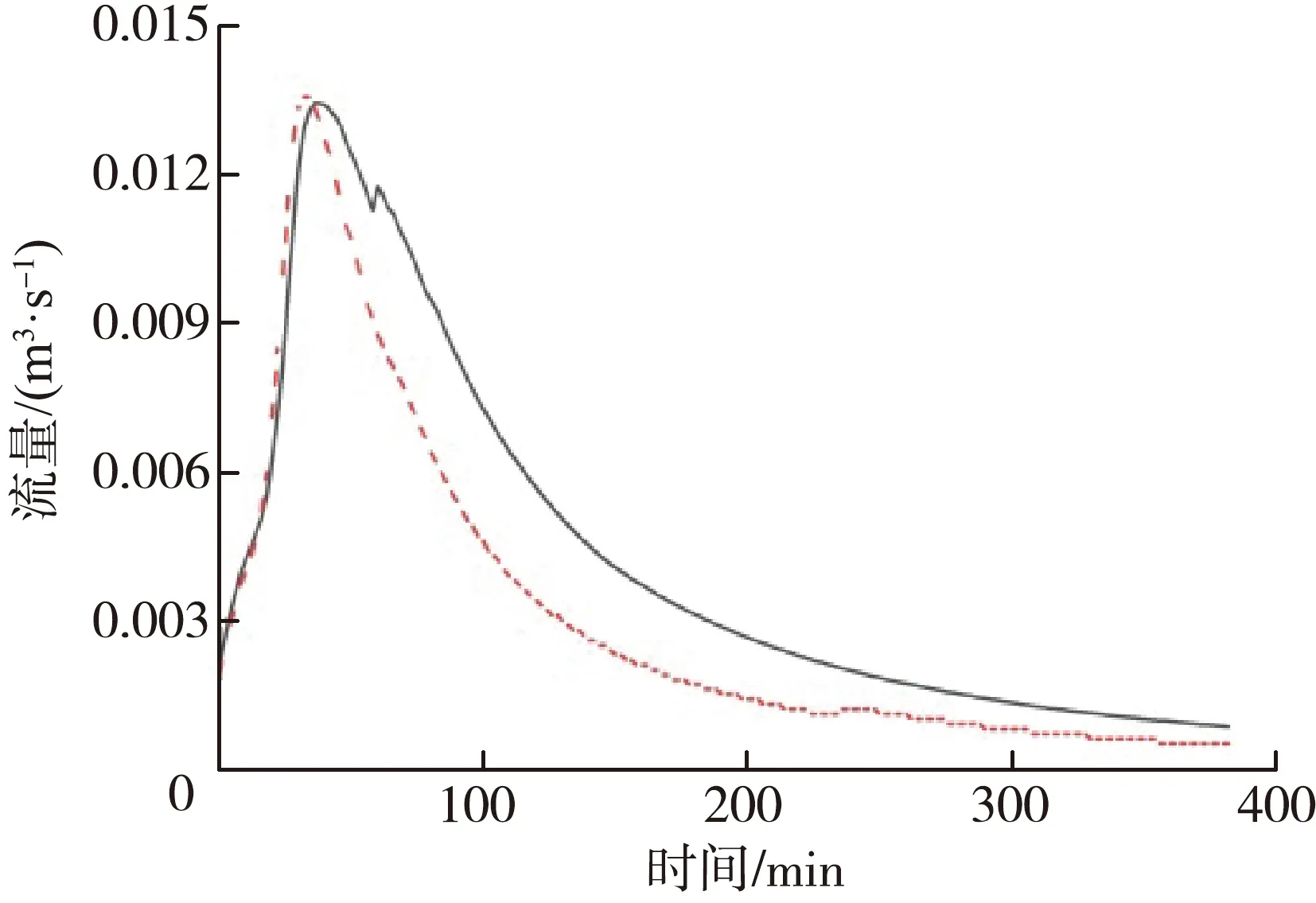
(a) 2017年8月20日
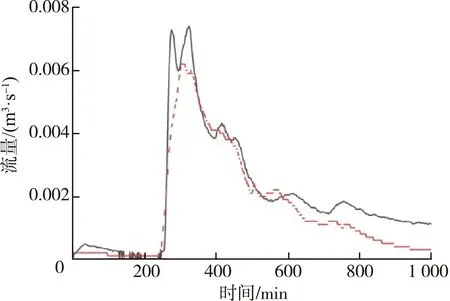
(b) 2017年9月9日

(c) 2017年9月16日

(d) 2017年9月26日图3 模拟值与实测值对比Fig.3 Comparison between simulated and measured values
采用2017年9月16日和9月26日的降雨径流数据进行模型验证。模拟数据与实测数据对比见图3。本文以纳什效率系数(Ens)对模型的模拟性能进行评估[35]。2017年8月20日、9月9日、9月16日和9月26日4场降雨事件的Ens分别为0.82、0.87、0.80和0.59,表明SWMM的水文水动力参数取值合理,所构建模型的可靠性高。由于该研究区缺乏实测水质监测资料,故参考相同地区研究数据资料[36],取得的水质模型参数见表2。

表2 水质模型参数Table 2 Parameters of water quality model
3 结果与分析
3.1 模拟结果
通过对45场设计降雨进行模拟,得到不同降雨条件下的径流控制率以及TSS、COD、TP和TN的削减率(图4)。由图4可见,在不同雨峰系数设计降雨条件下,设计降雨重现期小于20 a时,随着重现期的增大,径流控制率与污染负荷削减率下降速度均较快,设计降雨重现期大于20 a时,随着重现期的增大,径流控制率与污染负荷削减率下降速度均较缓,径流控制率与4种污染物的削减率随重现期的变化趋势基本一致,由此可推测出两者具有较好的线性拟合关系。
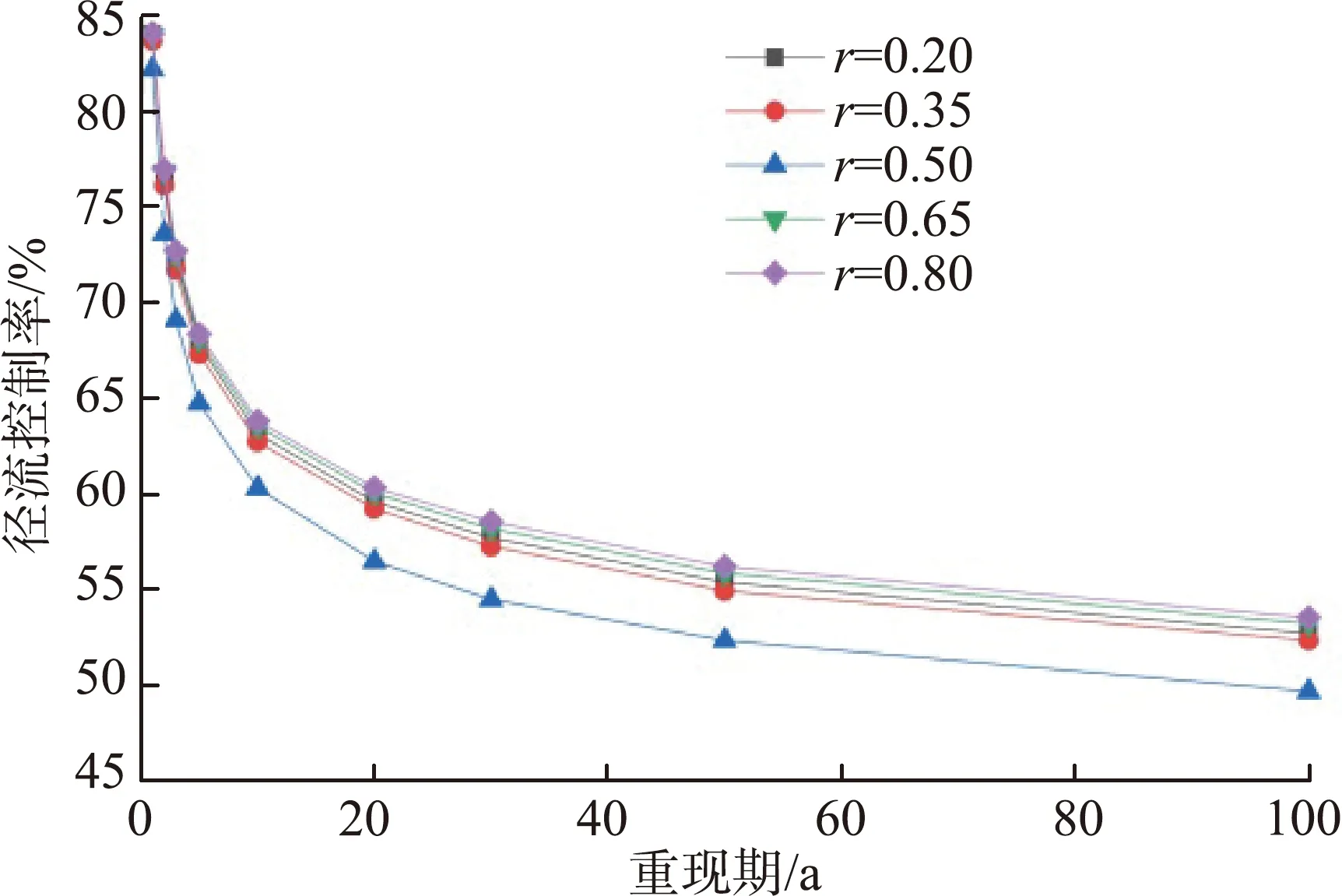
(a) 径流控制率

(b) 污染负荷削减率图4 不同降雨条件下的径流控制率与污染负荷削减率Fig.4 Runoff control rates and pollution load reduction rates under different rainfall conditions
3.2 径流控制率与污染负荷削减率对不同设计降雨的响应关系
由图4可知,设计降雨对径流控制率和不同污染负荷削减率的影响规律相似,故以TSS为例分析径流控制率和污染负荷削减率对45场设计降雨重现期的响应关系。不同雨峰系数对应的径流控制率与污染负荷削减率模拟数据如表3所示。由表3可见,不同设计降雨重现期对径流控制率与污染负荷削减率的影响较为明显。当设计降雨重现期从1 a变化至100 a,雨峰系数为0.50时,径流控制率与污染负荷削减率下降均最大,随着雨峰系数增大或减小,两者下降程度均呈减小趋势,表明径流控制率与污染负荷削减率有一定的协同关系。
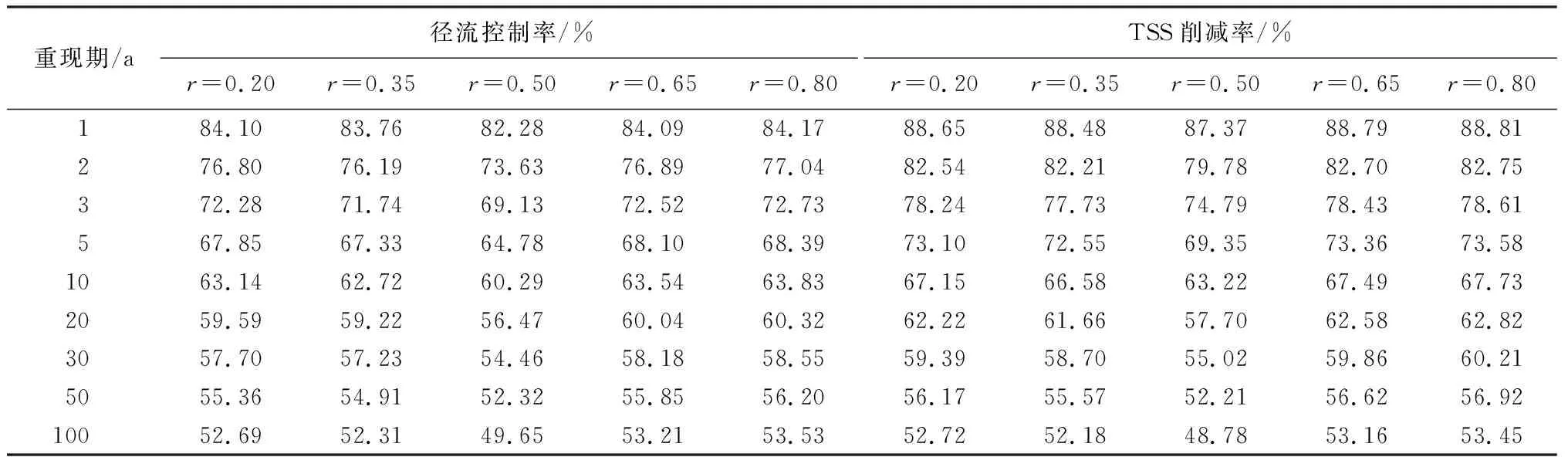
表3 不同设计降雨条件下的径流控制率与TSS削减率Table 3 Runoff control rates and TSS reduction rates under different design rainfall conditions
由表3可知,雨峰系数对不同重现期径流控制率与污染负荷削减率趋势相似,故以重现期为10 a的降雨条件为例,分析不同雨峰系数对径流控制率与TSS、COD、TP、TN负荷削减率的影响。表4为设计降雨重现期为10 a时的径流控制率与不同污染物的污染负荷削减率。
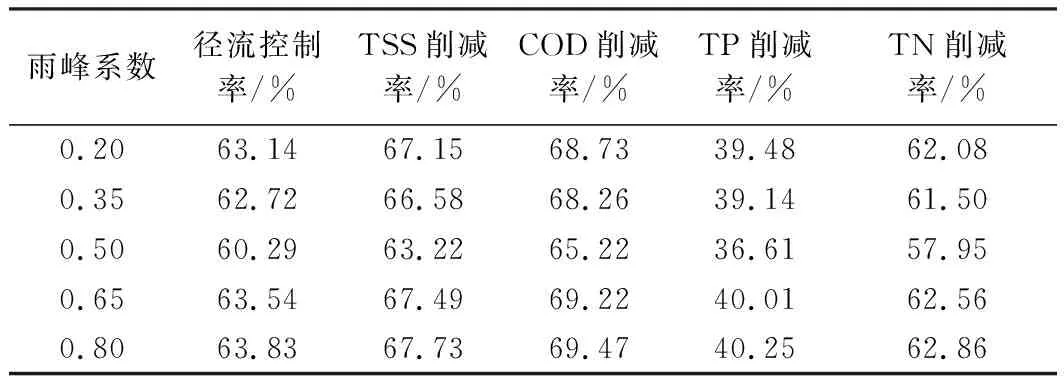
表4 设计降雨重现期为10 a时的径流控制率与 不同污染物的污染负荷削减率Table 4 Runoff control rates and pollution load reduction rates of different pollutants for a design rainfall return period of 10 a
由表4可见,在重现期为10 a的降雨条件下,当雨峰系数从0.20增加至0.80,径流控制率与污染负荷削减率均呈先减小后增加的趋势,当雨峰系数为0.50时,径流控制率和污染负荷削减率最小,随着雨峰系数的增加或减小,两者均呈增加趋势,径流控制率变化幅度在10%以内,TSS、COD、TP、TN削减率变化幅度均在5%以内,但相对于重现期对两者的影响,雨峰系数对其影响较小。这进一步表明径流控制率与污染负荷削减率具有较强的协同关系。
3.3 径流控制率与污染负荷削减率的协同关系
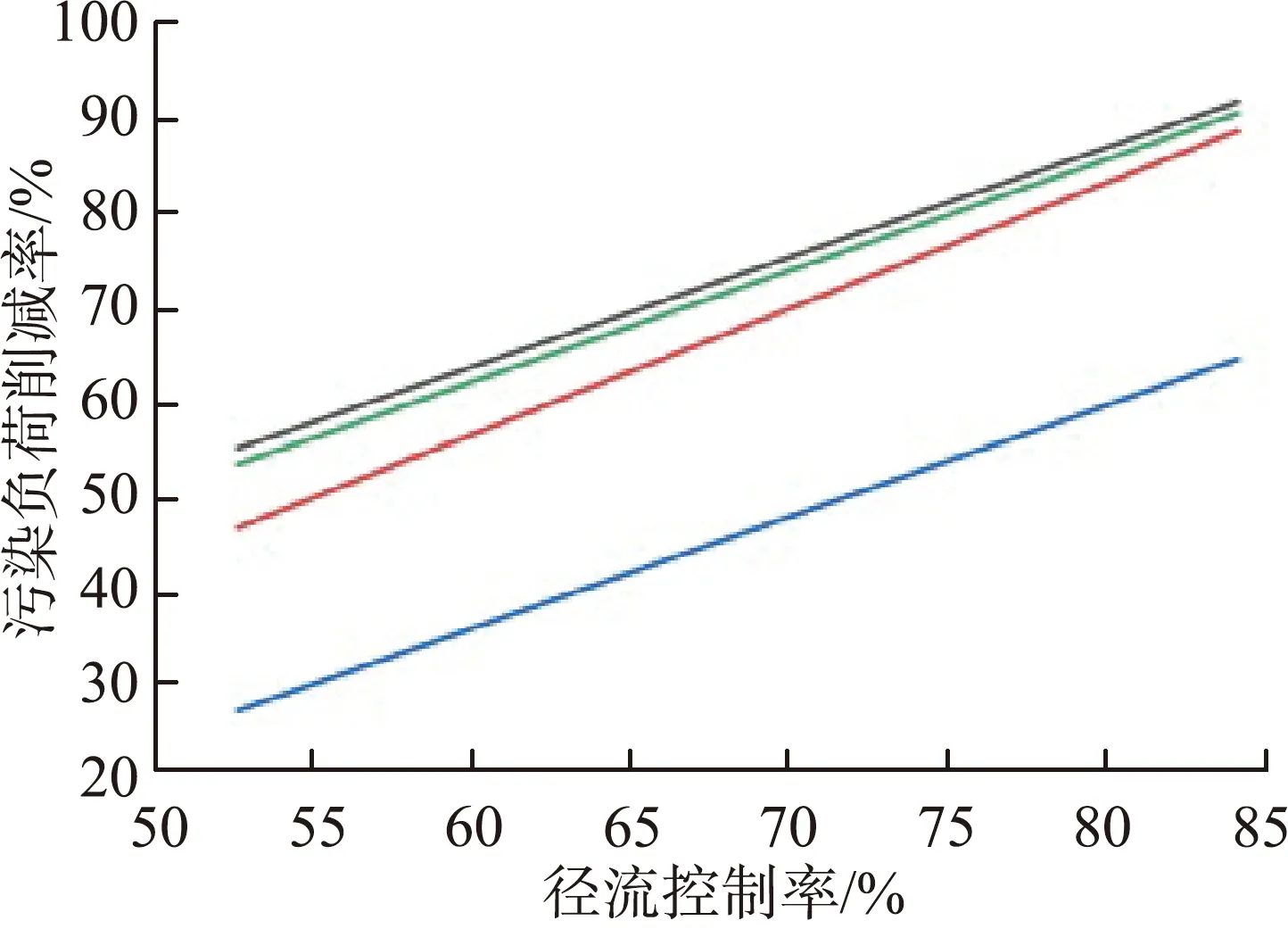
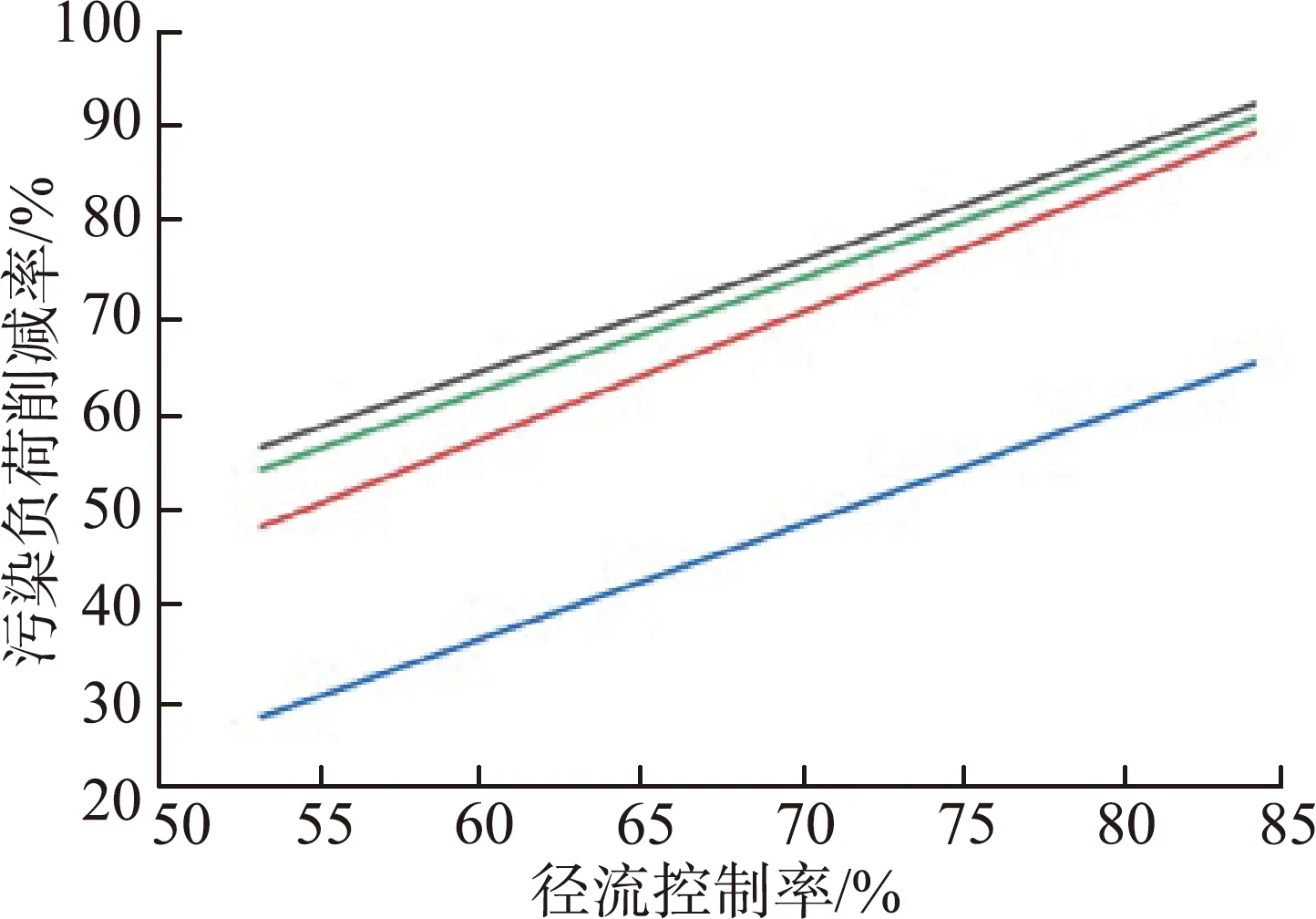
以上分析表明径流控制率与污染负荷削减率有一定的协同关系,通过对不同重现期降雨条件下的径流控制率与污染负荷削减率线性拟合,发现径流控制率与污染负荷削减率具有一定的线性关系,可拟合为线性函数,不同雨峰系数条件下COD、TN、TP、TSS 4种污染物的拟合函数曲线如图5所示,拟合方程与协同系数如表5所示。

(a) r=0.20

(b) r=0.35

(c) r=0.50
(d) r=0.65
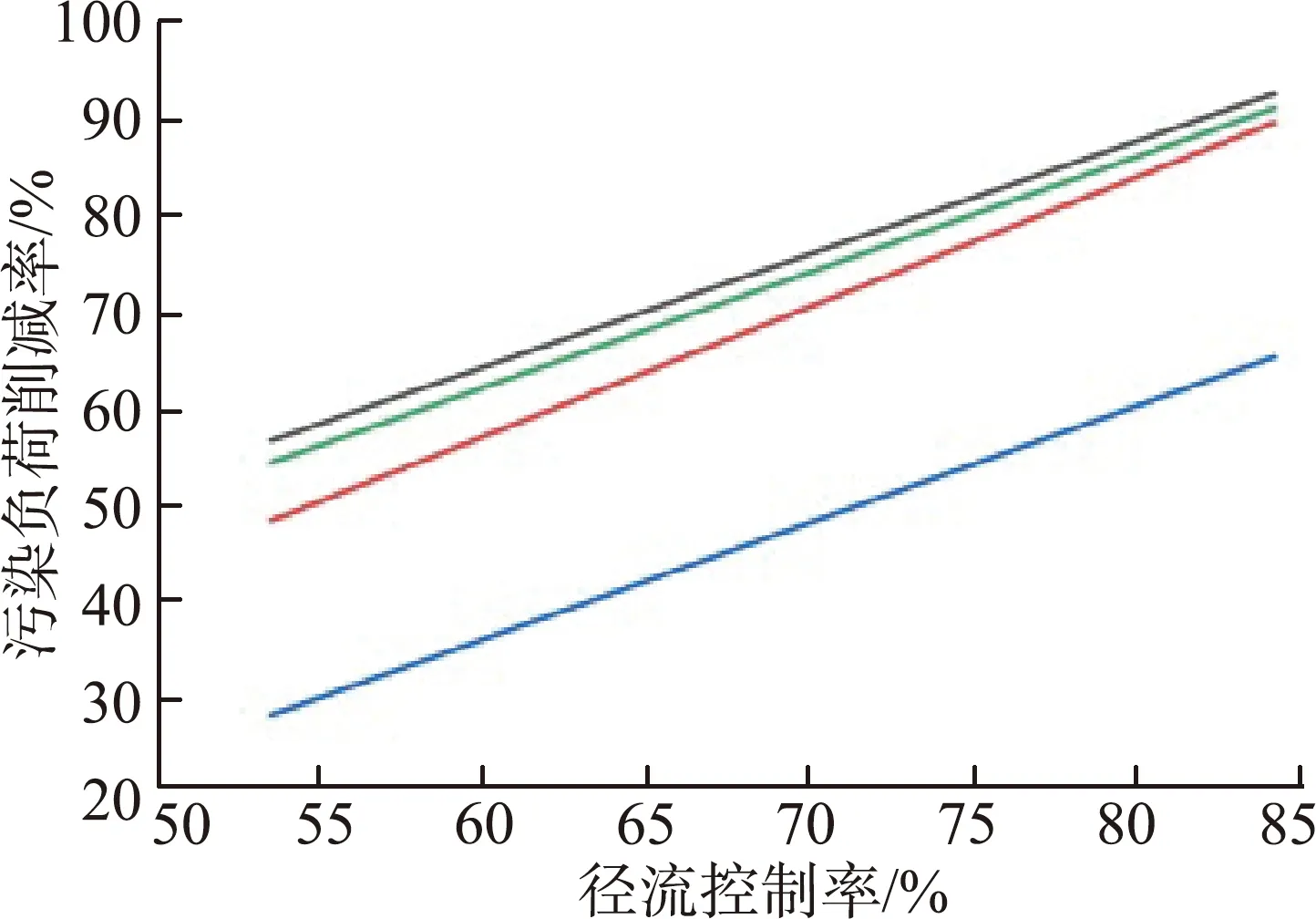
(e) r=0.80图5 不同雨峰系数的拟合函数曲线Fig.5 Fitted functions with different rainfall peak coefficients
由图5和表5可见,同一雨峰系数条件下,不同污染负荷削减率与径流控制率的拟合函数均为线性,且拟合曲线具有高度相似性,协同系数均大于0.989,表明以水量为载体的水质迁移规律均与水量输移规律密切相关。当雨峰系数从0.20增至0.80时,拟合函数曲线的斜率与截距相对波动幅度较小,雨峰系数对径流控制率与污染负荷削减率的协同关系影响不大。由于不同污染物本底特征不同,累积冲刷系数不同,故不同污染物拟合函数的斜率和截距有所不同。在不同雨峰系数条件下,污染负荷削减率均在拟合曲线附近。综上可知,径流控制率与污染负荷削减率拟合度较高,两者有着高度的定量协同关系。
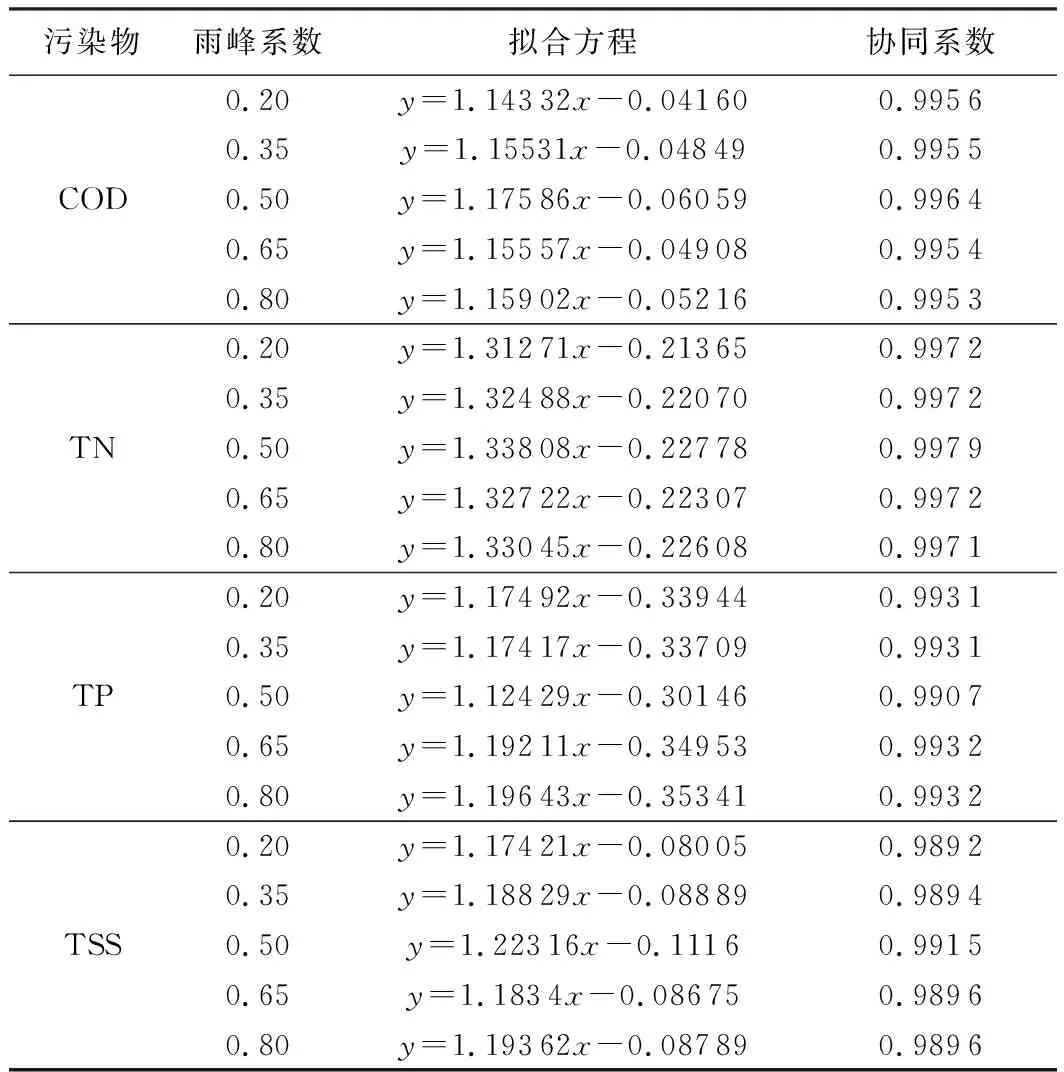
表5 拟合方程与协同系数Table 5 Fitting equations and correlation coefficients
4 结 论
a.重现期小于20 a时,随着重现期的增大,径流控制率与污染负荷削减率下降速度相对较快;重现期大于20 a时,随着重现期的增大,径流控制率与污染负荷削减率下降速度相对较缓,且随着重现期的增大,径流控制率与4种污染物的削减率的变化趋势基本一致,下降速度逐渐变缓。
b.在1~100 a重现期设计降雨条件下,重现期的大小对径流控制率与污染负荷削减率的影响较为明显,变化幅度在30%左右。当雨峰系数为0.50时,径流控制率与污染负荷削减率变化程度最大,随着雨峰系数增大或减小,两者变化程度呈减小趋势。
c.降雨重现期为10 a时,当雨峰系数从0.20增加至0.80,径流控制率与污染负荷削减率均呈先减少后增加趋势。当雨峰系数为0.50时,径流控制率和污染负荷削减率最小,径流控制率变化幅度在10%以内,TSS、COD、TP、TN削减率变化幅度均在5%以内,但相对于重现期对两者的影响,雨峰系数对其影响较小。
d.基于建筑小区尺度的径流控制率与污染负荷削减率有着高度的定量线性关系,雨峰系数对拟合函数曲线的斜率与截距影响不大,协同系数均大于0.989,拟合度较高,因此,可根据径流控制率推算出污染负荷削减率,为城市非点源污染研究提供参考。
