限制水域下喷水推进器水动力特性研究

2023-02-04丁江明刘建国张志远戴原星

船舶力学 2023年1期

龚杰，丁江明，刘建国，张志远，戴原星

（1.武汉理工大学高性能舰船技术教育部重点实验室，武汉 430063；2.武汉理工大学船海与能源动力工程学院，武汉 430063；3.中国船舶及海洋工程设计研究院喷水推进技术重点实验室，上海 200011）

0 引言

当船舶航行于港口、内河等限制水域中时，船舶的航行姿态、兴波特征及操纵响应等与深水状态存在明显不同[1-2]，船体周围的流动特性变化也会对推进系统产生一定影响。Sahin等[3-4]基于有限水深格林函数方法系统开展了潜艇、水面舰艇等的水压场理论建模和数值预报；缪涛等[5]采用面元法计算了有限水深条件下船舶水底压力分布特征。近年来，诸多学者基于粘性CFD 方法开展了船舶在浅水及波浪条件下的阻力特性的研究[6-8]，孙帅等[9]对标准船模KCS 开展了船模浅水效应的数值预报，重点分析了浅水条件下船舶阻力及流场的特点，研究发现当水深吃水比小于10 时浅水效应明显，螺旋桨盘面伴流分数均呈增大趋势。此外，孙帅等[10]对浅水条件下螺旋桨的轴承力特性进行了研究，研究发现浅水条件下螺旋桨轴承力时均值明显大于深水工况，脉动幅值随水深增加迅速减小。

喷水推进方式是一种适用于浅吃水条件的特种推进方式[11-12]。本文将通过CFD 方法计算得到喷水推进装置在无限水域和限制水域条件下的水动力性能和关键流场，分析不同水深条件下喷水推进器水动力性能变化，重点探讨开式循环水槽条件下浅水阻塞效应和侧壁反射对喷水推进装置水动力性能的影响机制，该研究有助于加深理解喷水推进船舶在限制航道中的推进性能特性。

1 数值模型建立

1.1 控制方程

本文基于Reynolds 平均方法（RANS）对无限水域和限制水域中喷水推进装置的水动力性能预报进行研究，数值模拟类型为三维、有粘性、非定常的两相流数值模拟。控制方程采用基于SIMPLE算法的压力耦合方程组求解，其中对流项采用二阶迎风格式进行空间离散，耗散项采用二阶中心差分格式进行离散[13]，采用SST（shear stress transport）k-w湍流模型封闭方程组，利用VOF（volume of fluid）模型进行自由液面的模拟。

1.2 几何对象及数值模型

本研究对象为某型尾板式喷水推进混流泵装置[14]，推进泵叶轮叶片数为6，导叶片数为11，二者叶数互质以避免共振并减小脉动振幅，流道平直段直径D=0.2 m，推进器轴心高度与自由液面高度齐平，喷水推进器整体安装于一方形简化船体尾部（见图1），船体水线长Lwl=3.0 m，船宽B=1.2 m，设计吃水T=0.2 m。

图1 喷水推进器及船体模型Fig.1 Geometry of waterjet ship and tested model

数值模型建立和网格划分均基于SATR-CCM+平台，数值模型中建立笛卡尔坐标系O-xyz，坐标原点O位于尾封板、船底板和中纵剖面的交界点，无限水域中数值计算域的长、宽、高依次为12Lwl（z方向）、4Lwl（y方向）和3Lwl（x方向），限制水域模型中数值计算域三向尺寸依次为12Lwl、0.6Lwl和0.8Lwl，其中，限制水域宽度尺寸依照开式循环水槽实际环境尺寸确定[15]，根据实际试验条件设定限制水域中水深h分别取5T、6T和7T。

推进泵叶轮旋转运动通过滑移网格技术实现，数值计算域分为静域（包含船体、流道、传动轴、导叶等）和动域（叶轮）两部分，二者通过交界面传递流动参数。对喷水推进器和船体表面进行面网格重构，生成表面三角化良好的高质量面网格，以面网格为基础生成含棱柱层和切割体网格的非结构体网格（见图2），对流道、推进泵、水线面、开尔文波形以及尾部射流安装区域等重点监测区域进行网格加密[16]，无限水域和限制水域模型中网格划分、加密区域及尺寸设定等保持完全一致。最终，无限水域模型中总网格数量为640 万，其中静域网格数为570 万、动域为70 万；限制水域模型中总网格数量为470 万（静域400 万，动域70万）。

图2 推进泵体网格分布Fig.2 Mesh distributions of waterjet pump

计算域边界条件设定如下：进口类型为速度入口，出口类型为压力出口，船体及喷水推进器表面均为无滑移壁面，无限水域模型中侧壁和底面类型设定为速度入口，而限制水域模型中侧壁和底面为无滑移壁面。

1.3 工况设定

数值模拟中设定船模航行速度V0=2 m/s，叶轮转速n依次选定为400 r/min、500 r/min、600 r/min、640 r/min 和750 r/min 五个转速，限制水域条件分别设定为h/T=5、6和7。数值计算中船体航行姿态保持不变，无自由运动，数值计算中重点监控泵特性关键参数（流量Q、扬程H、叶轮扭矩M）和关键位置处流场特征（进口获流区、泵进流面等）。数值计算中的数值收敛性判定准则如下：（1）各残差项下降至10-5；（2）主要性能参数（叶轮扭矩、出口流量等）不随计算时间发生明显的变化。

2 计算结果分析

2.1 数值计算精度验证

开展系列计算之前对航速V0=2 m/s、转速n=600 r/min、h/T=6工况下限制水域数值模型进行网格无关性验证，建立具有相同网格分布、不同网格密度的粗、中、细三套网格，选取喷水推进器流量Q为目标量，基于Richardson 外推法[17]进行验证和确认分析，其中三套网格细化比r=1.2，试验不确定度假定为4%，详细计算步骤见参考文献[18]。最终计算结果汇总如表1，其中，RG为收敛率，PG为准确度阶数估计，USN为数值不确定度，UV为确认不确定度。计算结果显示：流量结果数值不确定度约为1.55%，且在4.29%的不确定度水平上得到确认，其不确定度水平和类似的RANS模拟研究[19]较为接近，数值计算结果具有一定的可信度。后续数值模拟均基于中尺度网格开展计算。

表1 流量不确定度分析结果（V0=2 m/s,n=600 r/min）Tab.1 Results of uncertainty analysis of flow rates（V0=2 m/s,n=600 r/min）

2.2流场特性分析

限制水域条件下浅水阻塞效应导致船体周围的流速较无限水深情况时更大，船底流速增加部分ΔV称为回流速度[1]，回流速度的产生引起喷水推进器流道进流条件发生改变，在限制水域下船底水流的速度为V0+ΔV，因此，喷水推进器进口获流区的平均轴向速度会增加，不同水深条件下回流速度的变化明显，图3 为x/Lwl=0.4 位置处从船底板至底面沿水深方向相对轴向速度Vz/V0的分布对比结果。无限水域条件下，船底板下水流因过流截面变小仍存在一定加速，但随着水深位置增加逐渐接近于自由来流速度V0，但限制域条件下有限水深水底壁面会存在边界层，船底板至船底区域回流速度接近线性减小变化规律，不同水深条件下变化趋势基本一致。

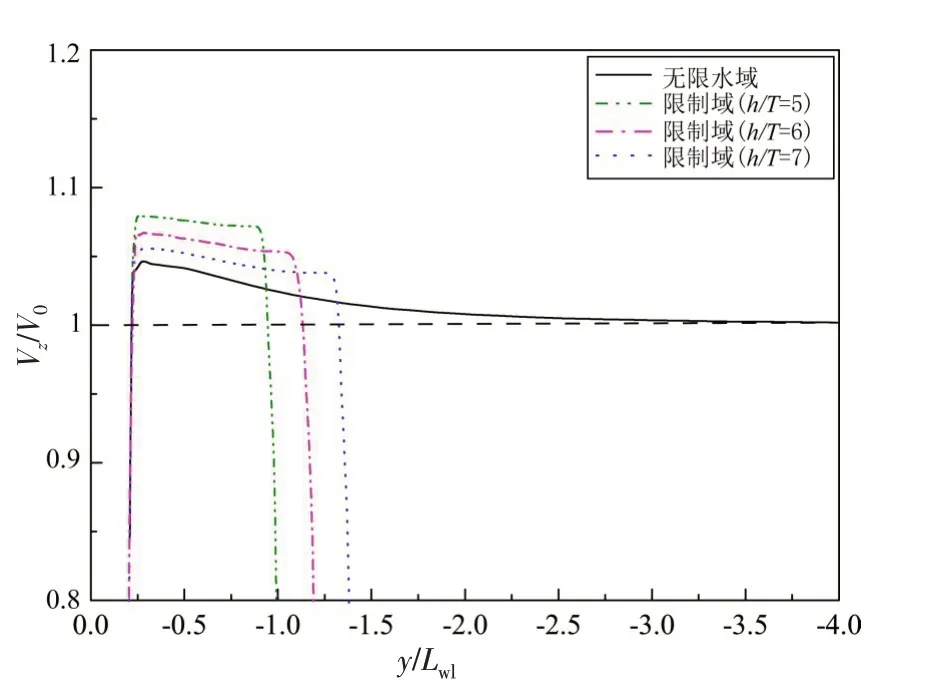
图3 沿水深方向相对轴向速度（Vz/V0）分布对比Fig.3 Comparison of relative axial velocity distribution（Vz/V0）in vertical direction

通过对流入喷水推进器流道内水流的反向追踪来确定进口获流区形状，使进口获流区流量和推进器喷口流量相等。图4展示的是转速n=600 r/min时无限水域和限制水域条件下进口获流区形状及轴向速度分布对比（h/T=6），图5 是不同转速下进口获流区的平均轴向速度（Vz/V0）在无限水域和限制水域中的对比结果（h/T=6）。

图4 进口获流区轴向速度分布对比（h/T=6）Fig.4 Comparison of axial velocity distributions in the capture area(h/T=6)

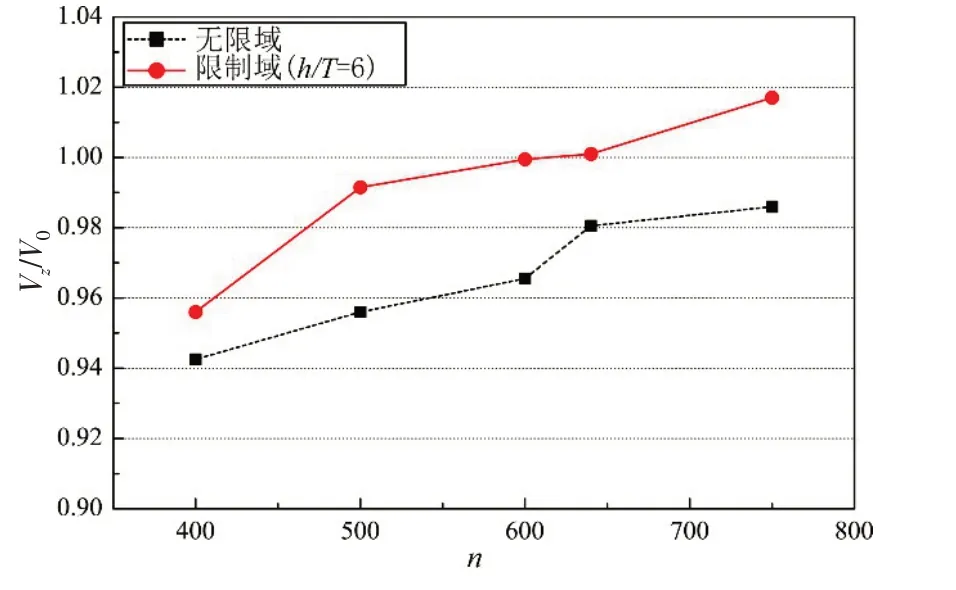
图5 进口获流区平均轴向速度分布对比Fig.5 Comparison of average axial velocity distributions in capture area

数值计算结果表明，无限水域条件下进口获流区平均轴向速度随转速增加而变大，但其相对值均小于1，限制水域条件下进口获流区平均轴向速度明显变大，且在高转速（n＞600 r/min）工况下相对平均轴向速度超过1。这说明一定工况下狭水道阻塞效应对喷水推进装置的进流条件会产生明显影响，随着水深吃水比h/T的减小，狭水道阻塞效应加剧，回流速度增幅更大，进口获流区平均轴向速度增加，此时船体航速V0应考虑相应的回流速度ΔV对基准工况设定进行修正。

浅水情况下波浪参数和波浪形状会发生改变，同时航道侧壁的存在会引起船体兴波的散波反射。从图6 无限水域和限制水域中自由液面兴波对比可以看到，侧壁对船体兴波的反射作用导致平船艏前端兴波加剧并大量出现向前翻卷的破碎波，限制水域中兴波开尔文角特征消失，兴波能量沿着侧壁传递并快速反射至船体周围，部分水流在船体舭部产生翻卷，对传递水流速度分布产生影响，浅水阻塞效应和侧壁的散波反射二者共同作用导致船体周围流动能量分布发生改变。此外，不同水深吃水比下自由液面形态变化差异不明显，侧壁限制是自由液面兴波特征形成的主导因素。

图6 无限水域和限制水域中自由液面兴波对比（h/T=6）Fig.6 Comparison of wave elevations between the open and restricted waters (h/T=6)

2.3 推进器水动力特性分析

限制水域环境下进口获流区轴向速度分布变化明显，但对喷水推进器进水流道的进速比IVR（IVR=Vpump/V0）的影响并不大，5 个转速下IVR值分布在0.8～1.5 之间，限制水域和无限水域下IVR的相对误差在0.3%～2.5%之间。出口非均匀度ζ和进水流道效率ηduct是评价进口流道性能的两大主要指标，其定义见文献[20]。不同进速比下流道出口非均匀度和流道效率结果如图7所示。不同进速比IVR下进口流道的性能存在差异，数值模拟结果显示：随着IVR的增加进口流道的出口非均匀度逐渐下降，随着内部流动发展得足够充分，非均匀度水平达到稳定值（约4%），限制水域环境下推进器流道的出口非均匀度会略大于无限水域情况，且水深吃水比越小二者差别越大，相对误差范围在0.5%～3.5%之间；流道效率在1.1＜IVR＜1.3范围内达到最高效率点（92.5%），三个水深吃水比下限制水域和无限水域下流道效率差别小于1%。

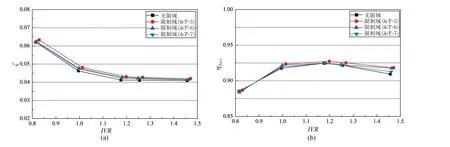
图7 不同IVR下进口流道出口非均匀度和流道效率变化Fig.7 Non-uniformity and efficiency of the channel under different IVR

对于完全相同的推进泵来说，限制水域条件带来的主要变化是其实际工作点发生改变，且其影响随着水深吃水比的增加而逐渐减弱。计算结果表明，限制水域条件下推进泵的流量、扬程、功率等外特性指标会发生小幅变化。图8 为不同IVR下进水流道流量系数KQ、扬程系数KH和泵效率ηpump的对比结果（h/T=6），泵特性系数定义见文献[15]。当前水深吃水比范围内，限制水域环境导致流量系数KQ和扬程系数KH偏高，其平均相对偏大值范围分别为0.2%～1.5%和1.0%～2.6%，泵效率ηpump（ηpump=ρgQH/2πnM）预报结果在试验范围内偏大0.9%～2.0%，这说明当前设定流量工况点已越过最高泵效点。