临兴区块致密砂岩气储层破裂压力预测方法研究

2023-02-03李德李宇杨天爽

石油工业技术监督 2023年1期

李德，李宇，杨天爽

中海油能源发展股份有限公司工程技术分公司（天津300450）

0 引言

我国致密砂岩气分布广，探明地质储量高达40%[1]，居非常规天然气产量首位，是潜力巨大的非常规天然气资源。2021年初，中国海油在山西省临县和兴县发现千亿立方米的大气田，探明天然气地质储量超过1 010×108m3[2]。

致密砂岩气简称致密气，一般指赋存于渗透率小于1×10-3μm2、孔隙度小于10%的砂岩储层中的天然气[3]。由于其具有低孔隙度、低渗透率特征，开采难度较大，通常需要大规模水力压裂措施才能产出具有经济价值的天然气。在现场压裂施工过程中，破裂压力是压裂工艺参数设计的核心要素，其预估的精确与否对压裂设备优选、提高压裂效益至关重要。在储集层改造过程中，某些地层破裂压力异常高，超过管柱及设备的承受能力，直接导致压裂改造措施失败[4-5]。因此，如何准确估计储层的破裂压力亟待解决。

1957年，Hubbert和Willis[6]首次提出基于线弹性理论的适用于非渗透条件下岩石破裂压力的计算模型。1962年，Morgenstern[7]引入剪切破坏理论来计算破裂压力。1973年，Daneshy[8]借助坐标系变换的手段建立了定向井井筒周围的应力分布模型，从而推导出定向井条件下储层破裂压力计算模型。1981年，黄荣樽等人[9-10]将地应力、孔隙压力、井内液柱压力以及压裂液渗滤对井周应力的影响引入了垂直裂缝和水平裂缝起裂的判断依据，从而提出一种新的破裂压力计算模型。1991年，Ito和Hayashi[11]引入点破裂准则来计算破裂压力，该准则认为岩石起裂位置在距井壁一定特征距离的特征点处。2002年，李传亮等人[12]建立了在射孔条件下的破裂压力计算模型。2003年，胡永全等人[13]采用有限元法对射孔条件下水力压裂后储层破裂压力进行了分析研究。2009年，王素玲等人[14]运用牛顿法研究了低渗透储集层条件下射孔参数对地层起裂压力的影响。

随着计算水平的提高，一些学者开始借助数理统计和机器学习的方法对储层破裂压力进行预测研究。2004年，聂采军等人[15]根据测井数据，提出一种基于数理统计方法的破裂压力预测模型。2014年，于成海和郭大立[16]建立基于径向基函数网络的煤层破裂压力预测方法。2015年，李昌盛等人[17]建立一种基于遗传算法优化BP神经网络方法的地层破裂压力预测模型。2018年，张啸宇根据压裂施工历史资料，提出基于多元线性回归和BP神经网络算法的两种破裂压力预测方法。2019年，陈立超和王生维[18]通过非线性拟合方法研究煤层破裂压力与弹性模量、剪切模量、泊松比之间的关系。

综上所述，国内外学者对地层破裂压力的计算和预测进行了大量的研究，但针对基于多元线性回归方法的破裂压力预测模型鲜有研究。基于此，以山西省临兴区块致密砂岩气储层为目标对象，根据构建的压裂施工资料、测井资料及地质数据的数据库样本，通过多元线性回归方法计算储层的破裂压力。为进一步剖析不同参数对破裂压力的敏感性，分别计算各因素与破裂压力的皮尔逊相关系数，从而评价最小水平主应力、弹性模量、泊松比、渗透率、孔隙度和破裂压力的关联程度。

1 地质情况

临兴区块地处鄂尔多斯盆地东北部伊陕斜坡东段、晋西挠褶带西缘，其面积约为2 530 km2。伊陕斜坡基岩起伏较小，沉积盖层坡度倾角较为平缓，主要形成于早白垩时期，该斜坡现今构造面貌为向西倾斜的平缓单斜，倾角不足1°，主要发育鼻状构造；晋西挠褶带位于盆地东缘，呈带状延伸。该构造带的东缘南部发育南北向的狭窄背斜构造，构造带的西部多发育南西向的鼻状构造。

晚石炭世-早二叠世沉积的海陆过渡相含煤层系是该区域上古生界的主力烃源岩，且在本溪组至石千峰组都是发育有利的储集层类型，在储集层的纵向上形成了下部（本溪组-山西组）、中部（下石盒子组）和上部（上石盒子组-石千峰组）3种成藏组合。由此可以表明，临兴区块是天然气富集的有利场所。

2 基础参数获取及计算

由于临兴区块各井及各层段压裂施工次数较多，研究选取了其中15口致密砂岩气井的20次压裂数据。将las文件测井数据导入GOHFER3D软件中，计算了不同压裂目的层条件下的最小水平主应力、弹性模量、泊松比等参数，孔隙度和渗透率通过地质资料获取得到。最终统计后的基础参数见表1。

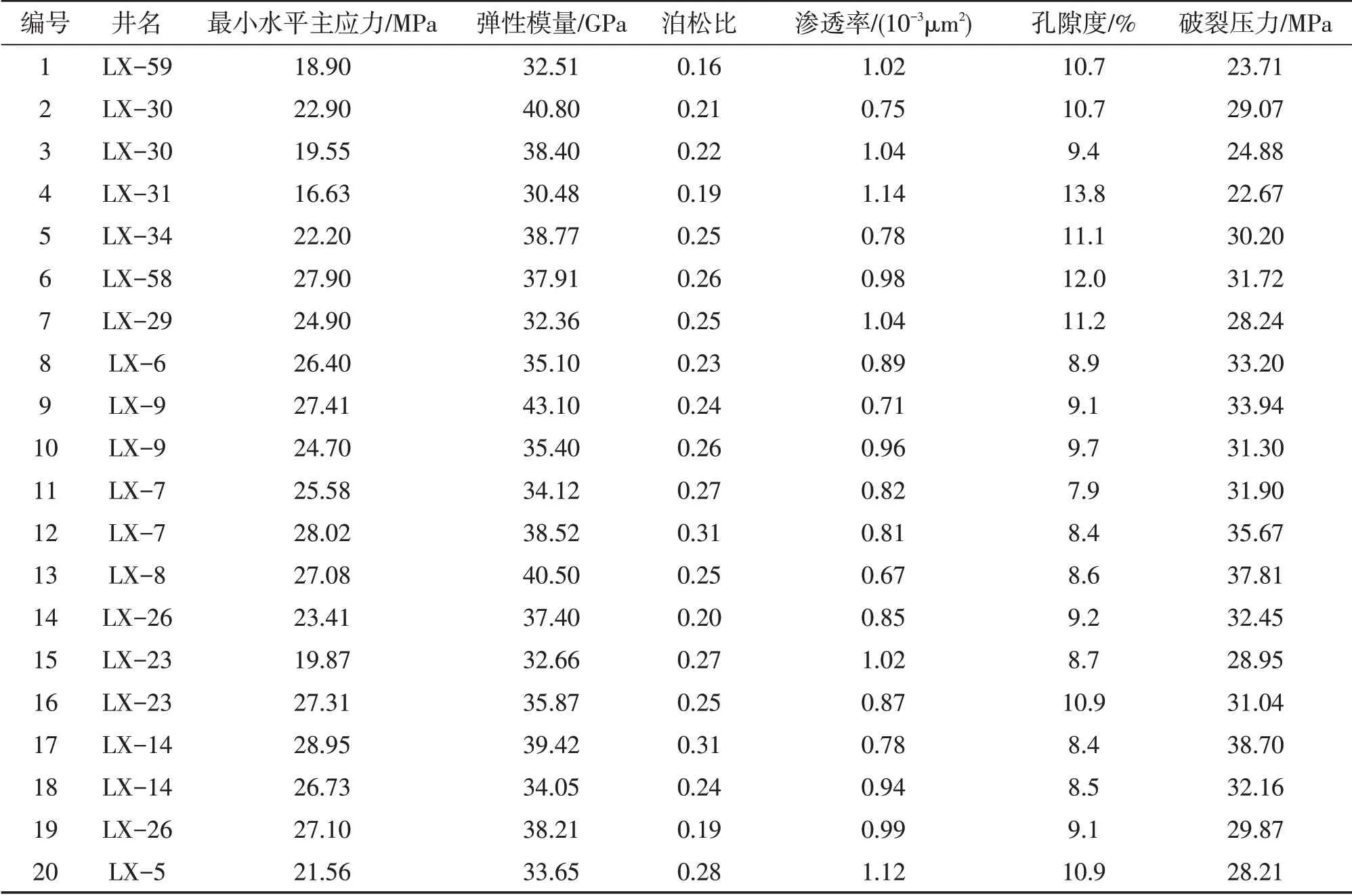
表1 临兴区块致密砂岩气压裂储层基础数据

3 破裂压力计算模型

3.1 多元线性回归模型

多元线性回归是一种线性预测多个自变量和因变量之间关系的数理统计方法，当仅有一个独立变量的时候称作一元线性回归。通常回归模型都假设每个因素是完全相互独立的，虽然这个假设在大多数实际问题中都不完全成立，但回归模型仍然被广泛地应用于岩石力学与压裂模拟领域的预测问题中[19]。假定模型中因变量y与p个因素相关，则样本点的多元线性回归方程通式为：

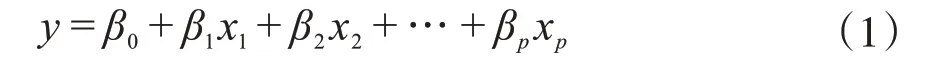
式中：β0，β1，β2，…，βp是模型所要计算的拟合参数；x p表示样本点的第p个自变量。

以储层的最小水平主应力、弹性模量、泊松比、渗透率、孔隙度为自变量，以破裂压力为因变量，多元线性回归后可得回归方程：

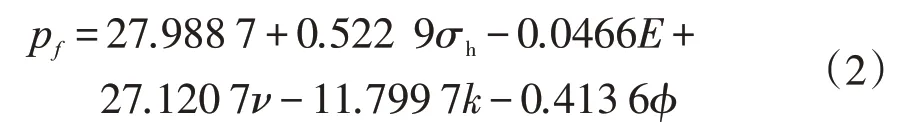
式中：p f为破裂压力，MPa；σh为最小水平主应力，MPa；E为弹性模量，GPa；ν为泊松比；k为储层渗透率，10-3μm2；φ为孔隙度。

根据图1的计算结果可以看出，利用多元线性回归方法预测结果与实际的破裂压力具有较高的吻合度。多元回归后的拟合优度为0.904 9，且p值小于0.05。从图2可知，预测值与实际值的压力差最大为2.37 MPa，85%的压力差计算结果小于1.7 MPa。由图3可知，基于多元线性回归预测后的破裂压力相对误差值不超过7.31%，平均相对误差为3.4%。

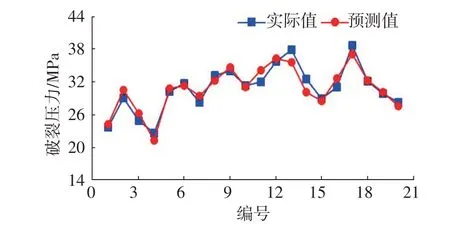
图1 多元线性回归预测破裂压力结果

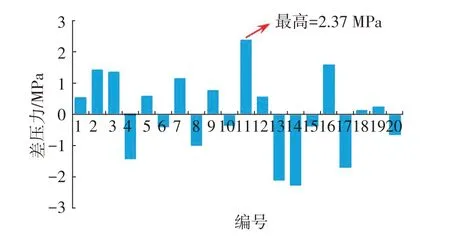
图2 多元线性回归预测破裂压力差应力结果

图3 多元线性回归预测破裂压力相对误差分析

3.2 传统破裂压力模型

为了与传统的破裂压力模型计算结果进行比较，对6种典型的破裂压力计算模型进行了统计与分析[20-23]，见表2。表2中σt为岩石的抗拉强度，MPa；σH为水平最大主应力，MPa；p0为地层压力，MPa；α为毕奥特系数,无量纲；A是中间参数，无量纲；K B为岩石体积模量，MPa；K M为骨架矿物体积模量，MPa；φ为孔隙度；T表示非均质地质构造应力系数；模型中S代表最小水平主应力，MPa；α、β分别为水平两个主应力方向的构造应力系数。

表2 传统储层破裂压力计算模型统计

根据表2的破裂压力计算模型可以得到各种方法下的破裂压力预测值，与现场实测值对比后的结果如图4所示。

图4 不同模型下破裂压力计算结果

根据图4的计算结果可知，不同模型的破裂压力计算结果均在实际破裂压力值附近，破裂压力值大多集中在20～40 MPa。为了评价各种模型的优劣性，还需分别计算破裂压力预测值与实测值的相对误差值（图5），以此来优选破裂压力计算模型。

图5 不同模型下破裂压力的相对误差

由图5可知，多元线性回归方法计算出来的破裂压力值的平均相对误差最小，仅为3.4%。Haimson-Fairhurst模型计算的平均相对误差最大，为10.26%。因此可以看出，选用多元线性回归模型来预测储层的破裂压力准确度较高。

4 敏感性分析应用

在数理统计学中，皮尔逊相关系数（Pcc）又叫做皮尔逊积矩相关系数，它是用来度量两个变量x和y之间的相关（线性相关）性，其取值范围在-1～1。其计算公式如下：

式中：cov(x,y)代表两个参数之间的协方差；σx、σy为两个变量x、y的标准差。

衡量破裂压力和最小水平主应力这两个变量间的线性相关性，就是把不同最小水平主应力值（样本点）组成一个样本集，以及对应的破裂压力值（样本点）组成一个样本集，然后按上述公式计算得到皮尔逊相关系数。其他变量与破裂压力间的皮尔逊相关系数计算方法类似。

各因素的皮尔逊相关系数计算结果如图6所示，最小水平地应力和破裂压力之间的皮尔逊相关系数为0.853 5，二者的线性相关性最强，最小水平地应力越大，破裂压力也有增加的趋势。弹性模量增加，总体来看破裂压力也有增加的趋势，但皮尔逊相关系数仅为0.585 6，二者间的线性相关性较弱。渗透率和孔隙度与破裂压力的关系为负相关，主要原因可能是孔隙度、渗迹率的增加使得地层孔隙压力升高，增大了破裂地层所需的驱动力，从而降低了破裂压力。