基于Python的MCM法评定加油机示值误差测量不确定度
2023-02-03练洪铭
练洪铭
玉林市检验检测研究院(广西 玉林 537000)
燃油加油机是对机动车所添加燃油体积进行计量,从而进行贸易结算的测量系统,是国家重点管理的计量器具,列入了强检目录实施强制检定。随着汽车成为家庭普遍的代步工具,人们对燃油加油机准确度的关注度随着燃油价格的上升也逐渐升高。燃油加油机示值的准确度关乎着老百姓的钱袋子,也关乎着公众对计量准确性的信心。这就要求计量人员严格控制检定过程各测量不确定度分量的产生,更加有效地消除检定过程中的误差,从而提升计量检定的准确度。因此,对燃油加油机示值误差的测量不确定度进行分析是至关重要的。测量不确定度是一个非负参数,是依据相关的信息,用于表征赋予被测量值分散性[1]。评定的方法有采用不确定度传递律法(GUM)和蒙特卡洛法(MCM)。目前,MCM法主要是使用MATLAB、MCM Alchimia等软件进行模拟,但因其使用收费及操作复杂性不能被广泛接受。而近期流行的高级动态语言Python具有免费开源、跨多平台、用途广泛、函数库齐全的优点,使用者可以交互式运行命令,能方便及时地调试、校验数据,非常适用于科学计算,因此也逐渐被计量工作者使用。基于以上分析,本文以评定燃油加油机示值误差测量不确定度为例,具体介绍了如何使用Python软件来实现MCM法评定,并将评定结果与GUM法的评定结果展开了对比研究。
1 实验部分
1.1 测量过程
依据燃油加油机检定规程,采用容量比较法,在最大流量点(0.9Qmax≤Q≤1.0Qmax),使用符合规程要求的标准器二等标准金属量器(容积为100 L,MPE±0.025 L)和辅助设备温度计(MPE±0.3℃),对加油机进行示值误差检定[2]。首先将检定介质汽油注入标准金属量器中直到加油机示值VJ达到100 L左右,读取标尺刻度H,计算20℃时的标准容积VB,再计算出汽油温度补偿后的体积VBt,用VJ减去VBt,重复测量3次,所得的差值的平均值,即为加油机的示值误差ΔV。
1.2 数学模型

式中:VB为20℃时标准器的标准容积,L;tJ为油枪出口油温(替代加油机流量计出口油温),℃;tB为标准器内油温,℃;βB为标准器材质(不锈钢)的体膨胀系数,为50×10-6℃-1;βY为检定介质(汽油)的体膨胀系数,为12×10-4℃-1。
1.3 测量数据
选择一台稳定的加油机重复测量10次,测得数据见表1。

表1 测量数据
测量时tJ平均值为30.5℃,tB平均值为30.2℃,取tJ-tB=0.3℃。10次测量,加油机示值误差的平均值----ΔV=0.115 L。
2 蒙特卡洛法(MCM)评定
2.1 MCM法特点
MCM法是一个对概率分布随机抽样进而散布传播的通用数值方法,当测量模型具有多个输入量且可由概率密度函数表征,并且输出量单一时,可采用MCM法评定,MCM法可有效克服GUM法理论假设和近似的不足,直接应用数学模型计算,不需要另外计算各分量之间的协方差,不会为简化评定过程而忽略部分影响因素,对于非线性传递模型,输入量的PDF明显非对称,输出量的PDF显著背离正态分布和t分布情况下的测量不确定度评定,MCM法更加准确可靠[3]。
2.2 MCM法评定步骤
MCM法是首先通过分析输入量X i的概率分布,获得X i的概率密度函数(PDF),然后对各PDF进行随机抽样,输入到数学模型中计算出yr,进而获得输出量Y的PDF,输出量的最佳估计值,标准不确定度和包含区间等信息可由Y的PDF计算得到,整个评定分为4个步骤[4]。具体评定流程及利用Python实现的方式见表2。

表2 MCM评定方法
2.3 Python完整代码
结合表1测量数据,MCM法评定测量不确定度的完整Python代码如下[5-6]。
#导入系统文件
import random
import numpy as np
from scipy import stats
#定义示值误差计算函数
def V_error():
VB=100.00-3.95*(H20-H)/1000#标准容积计算公式,计量颈f根据证书为3.95
VBt=VB*(1+βY*(tJ-tB)+βB*(tB-20))
ΔV=VJ-VBt
returnΔV
#循环模拟计算主体
M=1000000
#创建一个空数组接收输出量
ΔVs=[]
#循环M次
for i in range(M):
#H20为均匀分布,由证书得均值为97.88,半宽为0.025%,随机生成1个数值
H20=np.random.uniform(97.88*(1-2.5e-4),97.88*(1+2.5e-4))
#H为正态分布,以测量数据平均值46.77,标准偏差5.81为参数,随机生成3个数值,取平均值赋值H
H=np.mean(np.random.normal(46.77,5.81,3))
#βY,βB为正态分布,标准偏差均为2.5×10-6
βY=np.random.normal(12e-4,2.5e-6)
βB=np.random.normal(50e-6,2.5e-6)
#tJ,tB为均匀分布,半宽0.3℃
tJ=np.random.uniform(30.5-0.3,30.5+0.3)
tB=np.random.uniform(30.2-0.3,30.2+0.3)
#VJ为正态分布,由测量数据得期望值为100.00,标准偏差为0.0127
VJ=np.random.normal(100.00,0.0127)
#将各输入量输入到定义的函数中计算,结果赋值于ΔV
ΔV=V_error()
#将每个ΔV加入到数组ΔVs中,循环M次后结束
ΔVs.append(ΔV)
#对数组ΔVs运算,输出平均值及标准偏差
mean=np.mean(ΔVs)
std=np.std(ΔVs)
print("平均值为%f"%mean)
print("标准偏差为%f"%std)
#输出包含区间,平均值作为loc参数,标准偏差为scale参数
ΔVs_95=stats.norm.interval(0.95,loc=mean,scale=std)
print(ΔVs_95)
#以上代码,可根据实际测量数据,修改相关参数后,在Python编译器中运行,即可得结果,注意不要省略代码前的缩进。#后文字为注释,可省略。
2.4 MCM法评定结果报告
3 GUM法评定
3.1 测量不确定度来源
通过对加油机示值误差数学模型及测量过程的分析,测量不确定度的主要来源是测量重复性、标准器误差、温度计误差、金属量器及检定介质随温度变化而产生的误差等方面,如图1所示。

图1 不确定度主要来源
3.2 测量不确定度评定
各不确定度分量的详细评定可参考文献[7],本文不做详述,评定结果汇总见表3。

表3 不确定度分量评定结果汇总表
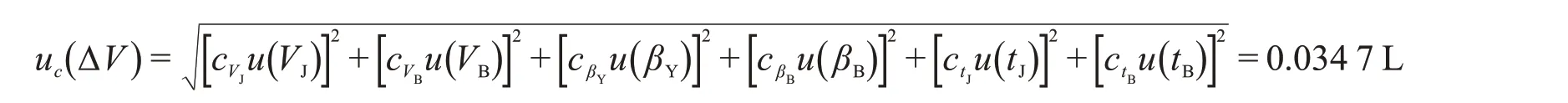
取置信概率p=95%,有效自由度veff=100,查分布表,k=1.984,则扩展不确定度为:
U95=k×u c=0.034 7×1.984=0.069 L
3.3 GUM法评定结果报告
4 MCM法与GUM法评定结果的对比
将MCM法和GUM法评定结果列于表4,并将包含区间在图2数轴上表示出来。比较两者的评定结果。MCM法评定的示值误差平均值及标准不确定度均略小于GUM法的评定结果;当置信概率p=95%时,MCM法评定的包含区间要略窄于GUM法评定的包含区间。其原因可能为:①GUM法假设各个变量不相关,保守估计了这些量值,评定结果增加了部分不可靠的测量不确定度;②GUM法评定计算测量重复性不确定度时,重复性引入的不确定度包含了数学模型中自变量导致的部分不确定度,对这部分不确定度进行了重复计算;③GUM法计算扩展不确定度的有效自由度时,各分量的自由度为估计值,计算出来的有效自由度为估算值,造成包含因子k的取值有差异。相比之下,MCM法评定是对各分量进行抽样,输入到数学模型中计算,避免了重复计算某些不确定度,而且能够将所有因素均考虑进来,使评定结果更为完整,更符合客观事实[9]。此外由计算机统计出置信概率的包含区间,更为准确,更为可靠。

表4 测量不确定度评定结果
基于Python模拟计算的MCM法,代码简洁,操作简单,相关模拟计算均由计算机完成,计算速度快,精度高,避免了人为疏忽造成的计算错误;评定过程无关数学模型的复杂性,不需要进行复杂的求导计算传播系数,也不需要计算复杂的自由度,可直接计算出结果。在计算的便捷性上,MCM法优于GUM法。

图2 两种评定方法包含区间在数轴上的比较
根据MCM法模拟计算的数据,绘制示值误差的分布直方图并拟合核密度估计曲线,如图3所示。可以看出,示值误差的概率分布具有正态分布的形态,符合GUM法基于中心极限定理的正态分布假设的理论基础,对GUM法评定的正确性进行了验证[10]。因此,在实际工作中,在简化及近似的情况下,GUM法可用于评定加油机示值误差测量不确定度,评定结果较MCM法稍保守,但差异不大。在准确度要求较高时,宜采用MCM法进行评定。

图3 概率分布直方图及核密度估计曲线
5 结论
通过本文的示例,MCM法评定测量不确定度具有适用范围广,评定过程简单、人工计算量少,计算精度高的特点,评定结果较GUM法客观、准确、可靠,可以作为GUM法的补充及验证。MCM法依赖于计算机进行模拟计算,而Python作为一种免费的高级可视化编程语言,具有编程简单、通用性强及硬件要求低的特点,其丰富的数据库、多样的函数及简洁的代码,能在MCM评定中快捷、准确地自动处理几何级倍数的数组、矩阵及向量运算,能简单便捷地获得平均值、标准不确定度、包含区间等内容并提供可视化的图表,给计量工作者在实际工作中运用MCM评定提供了可能。本文基本涵盖了MCM评定所需的Python代码,方便参考使用。
