周转铝箱的轻量化设计

邓昱琳，李光，曹菲

周转铝箱的轻量化设计

邓昱琳1，李光1，曹菲2

（1.天津科技大学 轻工科学与工程学院，天津 300457；2.天津职业大学包装与印刷工程学院，天津 300410）

以某周转铝箱作为研究对象，通过有限元分析方法和正交试验设计对周转铝箱进行轻量化设计，以解决结构强度设计过剩的问题。利用有限元分析软件Ansys Workbench对周转铝箱进行堆码工况的仿真分析，通过2个失效准则对分析结果进行评价，基于正交试验设计优化方案，通过Matlab软件对优化方案进行数学模型的建立及计算。通过仿真分析，第1阶模态载荷因子为6.98，基于失效准则，周转铝箱的安全余量较大。根据极差分析，以箱体自身质量为唯一指标，确定了周转铝箱箱体侧柱厚度尺寸对箱体自身质量的影响最大，继而通过Matlab进行数学模型的建立以及计算，轻量化方案在满足工况使用条件的同时箱体的自身质量减少了9.88%。轻量化设计后的周转铝箱符合强度失效和稳定失效2个准则，且满足实际工况使用条件，进一步说明采用正交试验法和有限元分析法进行轻量化设计的方案是可行的，实现了成本的减少，也提高了材料的利用率。

周转铝箱；轻量化；正交试验；有限元

金属包装箱其经济产值约占我国包装行业产业总量的五分之一，存在着很大的市场需求空间[1]，因此，周转铝箱的研究对包装行业具有必要性。随着汽车零部件、精密仪器等行业的飞速发展，包装行业对周转铝箱的需求也大量增加[2-3]。目前，多数企业对周转铝箱的设计往往依据经验，存在过度设计的现象，随着铝材价格的不断上涨，也迫使周转铝箱向轻量化设计方向发展，然而对该类规格较大的结构直接进行试验分析较为困难，为解决这一问题，将正交试验和有限元法相结合，根据多因素、多水平进行轻量化方案的设计[4]，基于失效准则验证轻量化结果。

李志强等[5]基于正交试验进行了优化方案的设计，并结合有限元的方法对支撑结构进行优化设计的验证，确定了结构设计的合理性。邱自学等[6]通过正交试验设计了6种优化结构，获得的最优结构质量减轻了466 kg。高志来等[7]采用正交试验设计了多种方案，基于Ansys软件对滑枕进行结构分析，所获得的轻量化结果显著。鞠家全等[8]采用三因素四水平正交试验设计方案，并使用Ansys软件对机床进行了静态和动态分析，最终获得的优化结构质量减轻了473 kg。杨思瑞等[9]通过正交试验法建立回归方程，结合数值模拟进行优化方案的验证，得到最优熔覆层质量。Wu等[10]基于正交试验法对不同因素下的喷射器进行了优化，结果表明优化后的结构性能更佳。

综上，国内外学者通过正交试验与有限元分析结合运用，达到了理想的轻量化结果，但是在正交试验的应用时，学者们仅考虑试验的优化成果，即主次因素，未考虑到优化成果的可靠性。文中以某公司周转铝箱为例，针对正交试验方案的可靠性问题，开展基于2个失效准则的轻量化设计。首先进行失效准则的判断；然后根据正交试验获取方案，结合统计学对建立的参数回归方程进行可靠性检验；最后结合Matlab软件中的优化工具箱对箱体进行轻量化设计，并通过失效准则进行验证。

1 有限元分析

周转箱在流通过程中主要处于堆码状态，结合实际工况，采用Ansys有限元分析软件进行堆码模拟，并根据分析结果对失效准则进行评价。

1.1 基本参数

周转铝箱材质为6061铝合金，箱体为44.11 kg，箱体外轮廓尺寸为1 200 mm×800 mm×1 155 mm。根据GB/T 228.1—2010[11]进行拉伸试验获得材料参数，弹性模量为9 392.87 MPa，泊松比为0.33，密度为2.75 g/cm3，屈服强度为275.41 MPa，抗拉强度为234.76 MPa。

1.2 失效准则评价

1.2.1 屈服强度失效

许用应力是工程结构设计的基本数据，以屈服极限为基准[12]，通过屈服强度的失效作为箱体失效的判断依据，需要满足结构所承受的最大应力不超过许用应力，判断式见式（1）。

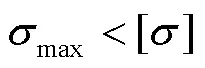
式中：max为最大应力；[]为许用应力。

结构的许用应力[]与屈服强度的关系式见式（2）。

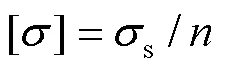
式中：s为屈服强度；为安全系数。

安全系数在静态工况下一般取1.5，根据式（1）和（2）联立计算得到材料的许用应力为183.61 MPa。

1.2.2 稳定性失效

为深入探讨箱体在荷载工况下的结构稳定性，鉴于箱体常处在满载时堆码的状态，易发生危险状况，因此针对箱体堆码工况进行屈曲模态分析，以测算其不稳定状态临界点，并测算结构安全因子。屈曲在结构分析中，主要有2个功能[13]：利用载荷因子估算结构的失稳或临界负荷；对结构材料进行分析并估算其安全因子，安全因子为极限强度与设计承载力的比值。

1.3 有限元模型

Ansys中选用实体单元Solid186对周转铝箱进行模拟。为了减少求解时花费的时间及计算机资源的过度占用，将周转铝箱模型进行简化，去除非关键部位，如螺钉、锁扣等部件，并考虑整个箱体承重部位主要位于梁、柱，因此将箱体面板忽略，简化后的模型见图1。考虑箱体属于多体部件，网格划分采用扫掠划分法，为了保证网格质量，进行了三层网格划分，划分后的单元为302 417个，节点为743 161个。

图1 有限元模型

1.4 堆码工况分析

周转铝箱满载时箱体总质量为300 kg，内装物作用于箱体底部托盘长短梁。根据实际工况，运输时采用两层堆码，上层箱体对下层箱体所施加的载荷设置于箱体顶部，需要注意接触面应与箱体底部地面接触部分重合。对箱体固定约束部分为箱底部。

对周转铝箱堆码工况进行静力模拟分析，应力计算结果见图2。最大应力点出现在箱体顶部横梁处，主要原因为该处结构为点焊连接，最大应力值为36.11 MPa，满足许用要求。屈曲模态分析结果见图3，一般仅用第1阶屈曲模态定义屈曲载荷，可见模态的失稳发生在箱体顶部结构，同静力分析确定的最大应力点所处位置一致，进一步说明该处的结构强度有待提高，且侧柱未发现失稳现象。基于失效准则，分析获得周转铝箱的安全系数为6.98，安全余量较大，也说明轻量化空间较大。

图2 堆码工况应力云图

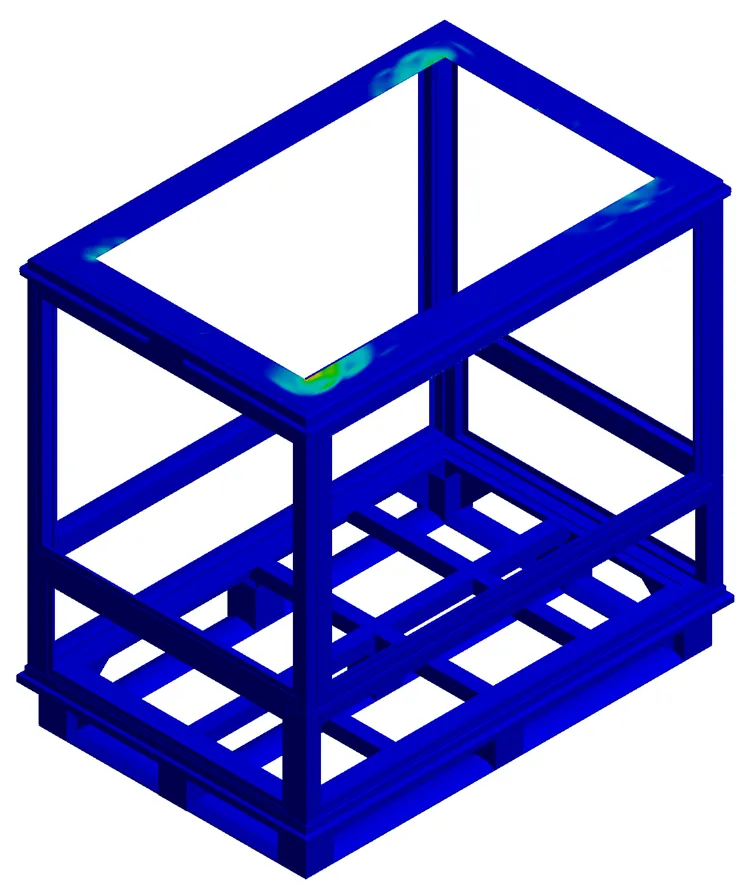
图3 屈曲稳态分析

2 轻量化设计

2.1 正交试验方案设计

在现有试验设计中，因为正交试验设计精度高、计算简便等原因，多采用正交法进行试验设计[14]，因此，文中周转铝箱的轻量化试验方案将采用正交试验进行设计，基于有限元分析结果，采用4因素3水平的方案设计，各因素及水平的数值见表1。采用正交表9(43)来进行试验[15]。

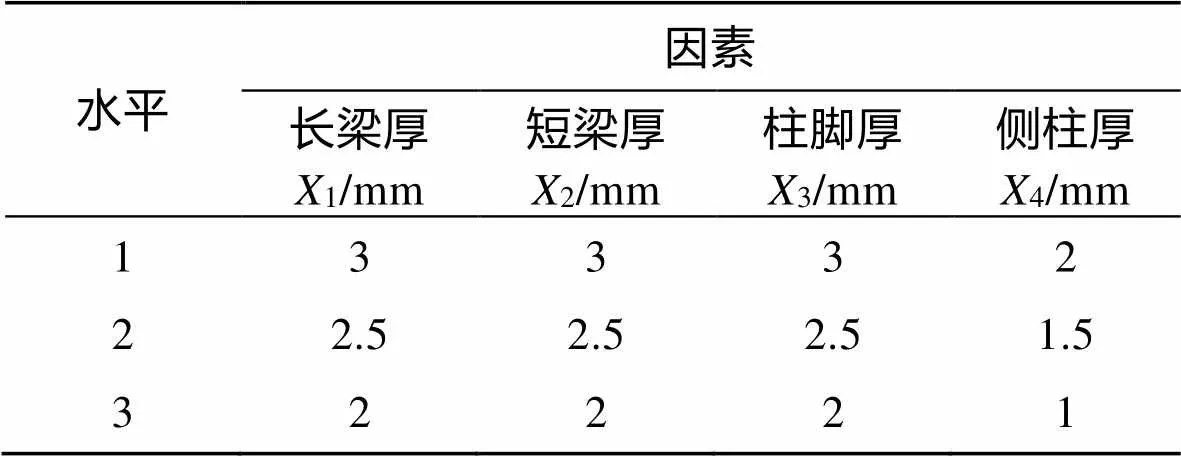
表1 试验因素水平

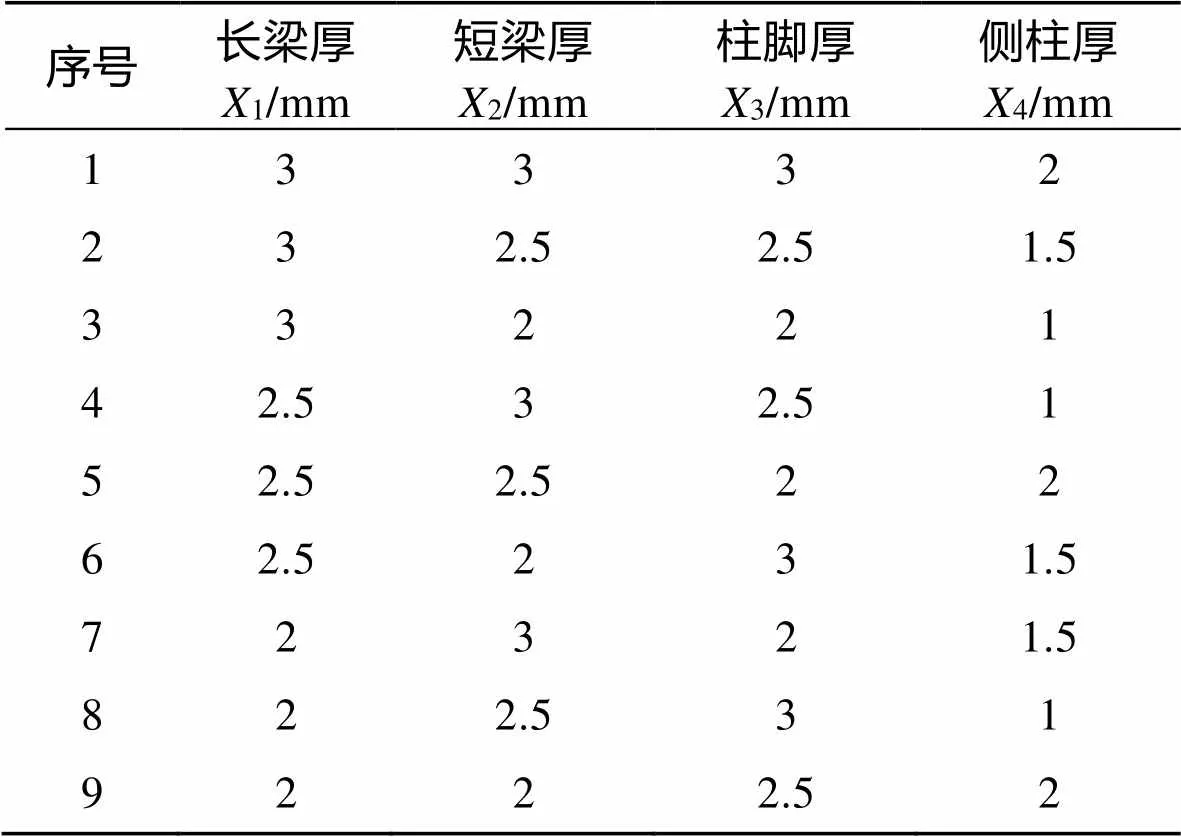
表2 轻量化试验方案

2.2 有限元分析

根据表2所设计的正交试验方案对模型重新构建后进行有限元分析，获取变形、应力结果，见表3。

2.3 正交试验结果分析

通过直观分析法可以找出影响优化最高的条件。将箱体自身质量作为优化目标进行直观分析，分析结果见表4，通过极差分析获得的极差值可以看出侧柱厚度是影响较大的参考因素。

文中依据研究对象，以周转铝箱的自身质量为唯一指标，根据直观分析法获取的数据绘制极差分析折线示意图，见图4。根据箱体自身质量极差分析结果以及极差分析折线图，获得影响因素从大到小的排序关系为侧柱厚4、长梁厚1、柱脚厚3、短梁厚2。

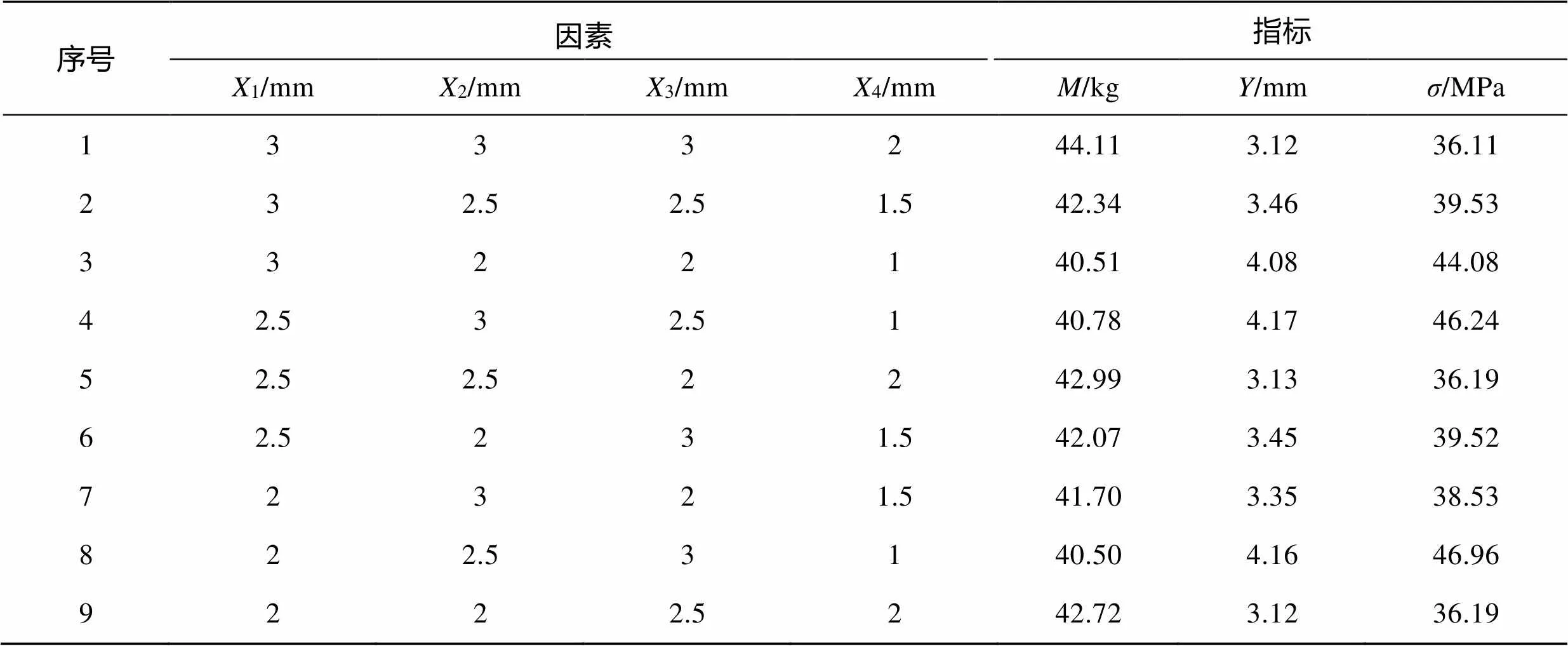
表3 轻量化方案有限元分析

表4 试验结果极差分析

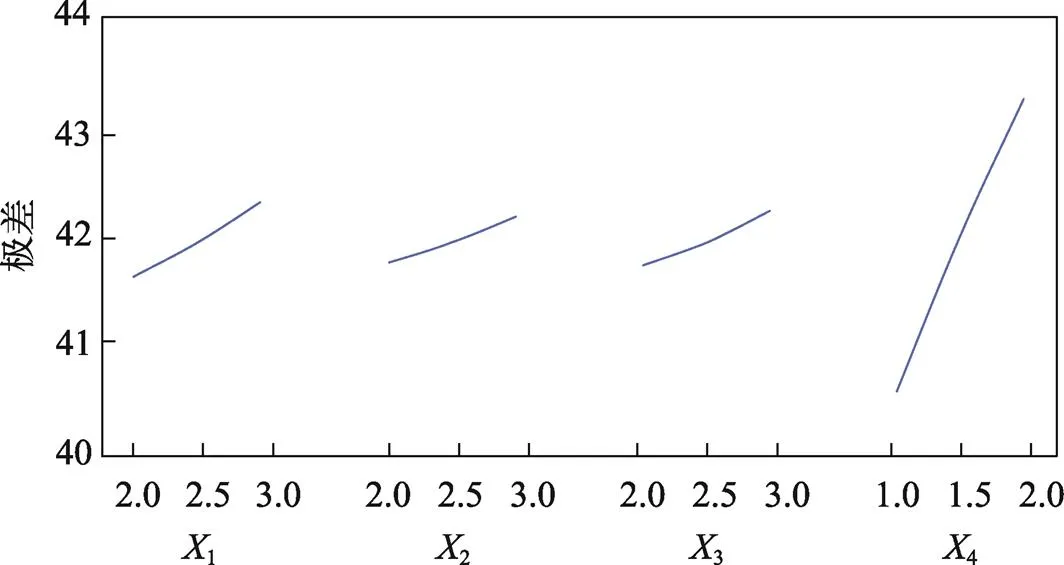
图4 极差分析折线示意图

2.4 优化模型的建立

2.4.1 建立回归方程

通过Matlab软件调用regress函数可以进行线性回归方程的拟合，将实验数据代入该函数中便可获得周转铝箱的最小箱体自身质量、最大位移、最大应力的回归系数。

根据计算得到最小箱体自身质量、最大位移、最大应力的线性回归方程分别如下：

最小箱体自身质量回归方程：

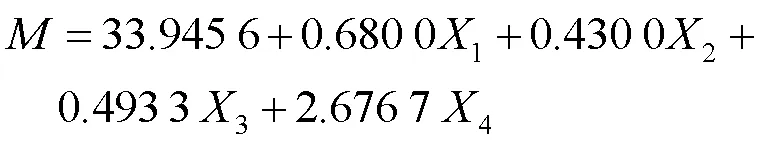
最大位移回归方程：

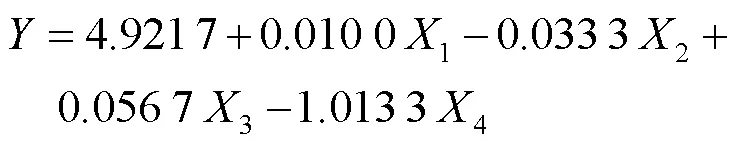
最大应力回归方程：

为了验证数学模型的有效性，还需要获得相关参数2、检验、检验的值。相关参数2无限接近1时，回归方程显著；检验也称为联合假设检验，(0.05)(5,3)=5.41，当满足>(0.05)(5,3)时，表明回归方程在95%的水平下显著成立；检验的值是一个递减指标，表示了结果的可信水平，值越大，结果越不可靠，若=0.05，则表明存在5%的可能是由偶然性造成的，因此要控制值在0.05以下即可认为存在统计学差异。

根据表5中结果所示，3个回归方程检验均满足，证明所拟合的数学模型有效。

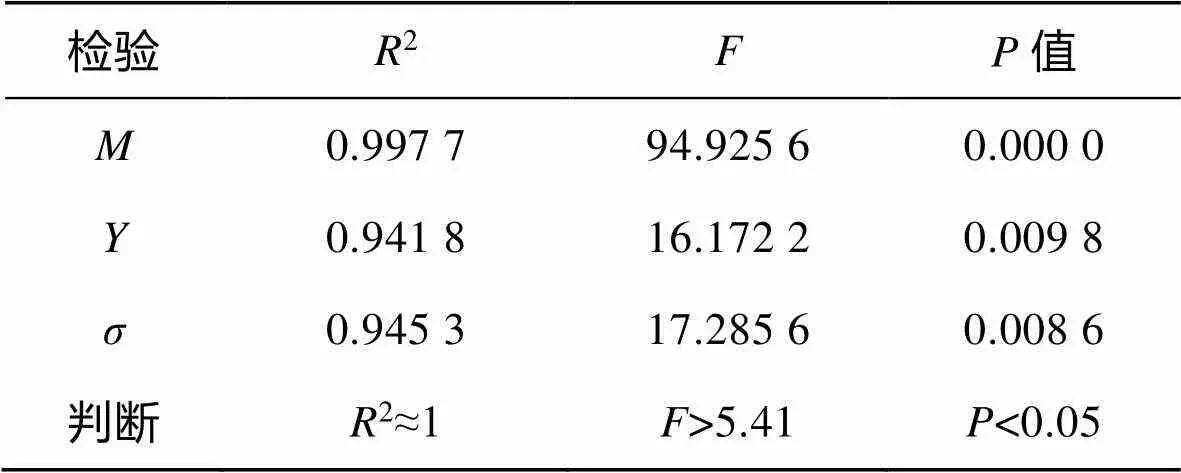
表5 检验结果

2.4.2 轻量化设计的数学模型

以周转铝箱自身质量达到最小值为目标函数建立优化数学模型，其中包括设计变量、约束条件及目标函数。优化数学模型表示为：

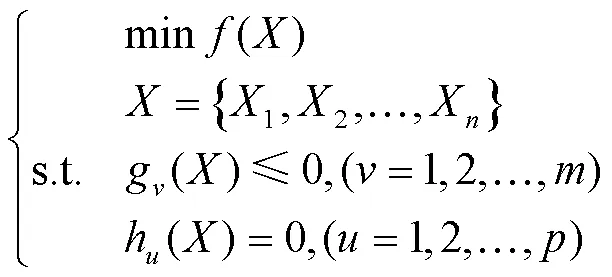
根据式（6）可知，该优化模型是通过约束条件解决最小值问题，当目标函数及约束条件至少具有一种非线性函数时，该类问题为约束优化问题，即存在限制条件的非线性规划问题，该类问题可通过调用Matlab中的优化函数进行求解。

2.4.3 轻量化数学模型的建立

2.4.3.1 目标函数的建立

在周转铝箱满足实际工况的条件下，以箱体自身质量最小化为目标设置目标函数：

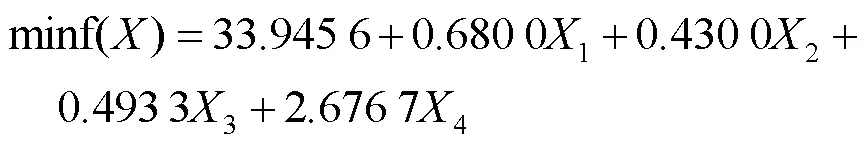
2.4.3.2 设计变量及约束条件

根据正交试验方案，共有4个因素，分别为长梁厚1、短梁厚2、柱脚厚3、侧柱厚4，设计变量为：

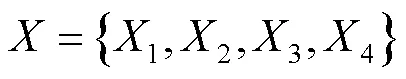
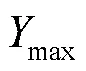
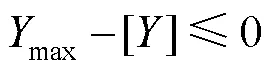
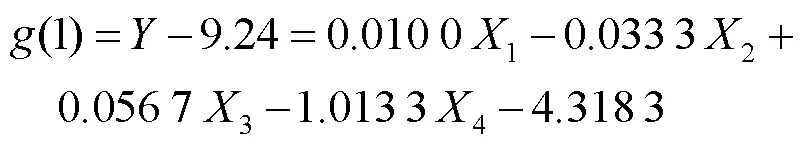
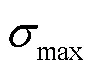
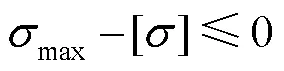
最后还需要对涉及的4个因素零件的尺寸进行约束，如下：

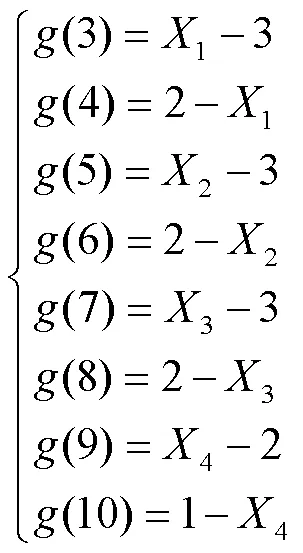
2.4.3.3 数学模型的建立

根据目标函数、设计变量及约束条件的分析，不涉及等式约束条件，构造周转铝箱轻量化设计数学模型为：

最终对所建立的数学模型求解目标函数的最小值。

2.5 轻量化结果及验证

2.5.1 轻量化结果

根据Matlab软件中优化工具箱常用函数fmincon函数对有约束的非线性问题进行最小值求解，优化结果见表6。

表6 优化结果

2.5.2 优化结构验证

根据对优化方案进行有限元分析，应力云图见图5，分析结果见表7，所获最大位移、最大应力值均在许用范围内，故优化后的结构符合使用。根据方案结果的对照，优化后箱体自身质量减轻了4.36 kg，降幅达9.88%。

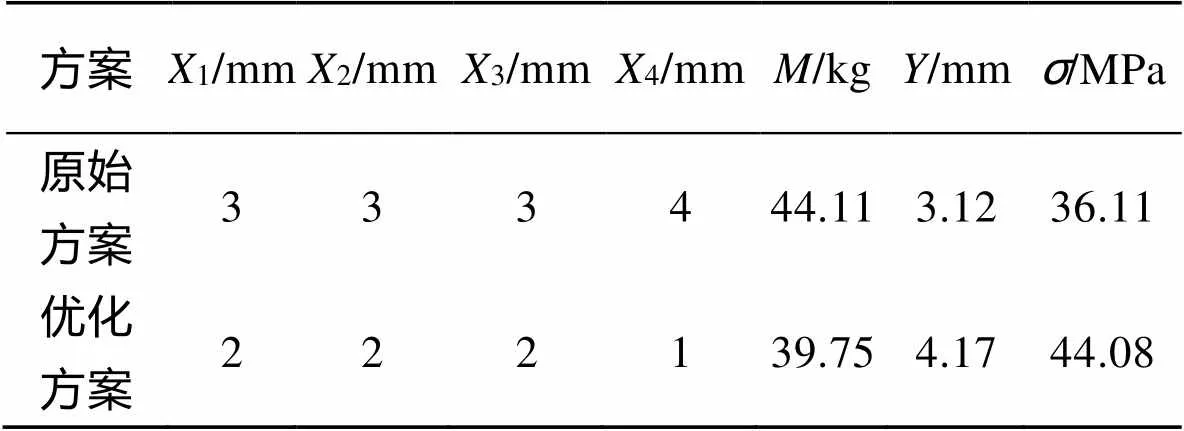
表7 方案结果对照

轻量化设计后的屈曲模态见图6，一阶屈曲特征值为4.06，符合稳定性失效准则。经过对原有方案设计与结构优化方案屈曲模态分析后的比较证明，原有设计方案中的失稳状态主要产生在箱体堆码接触面，经过轻量化方案设计后，屈曲同时出现在多个侧柱构件上，说明整体轻量化设计增加了构件变形的一致性。

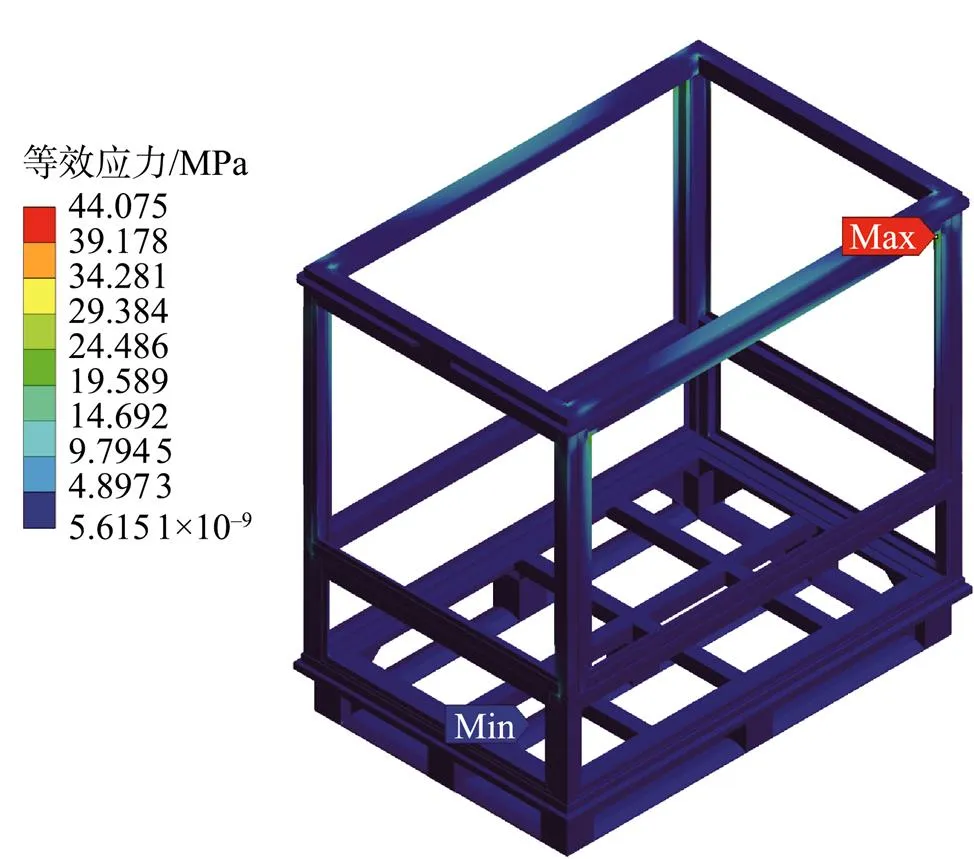
图5 优化后的堆码工况应力云图

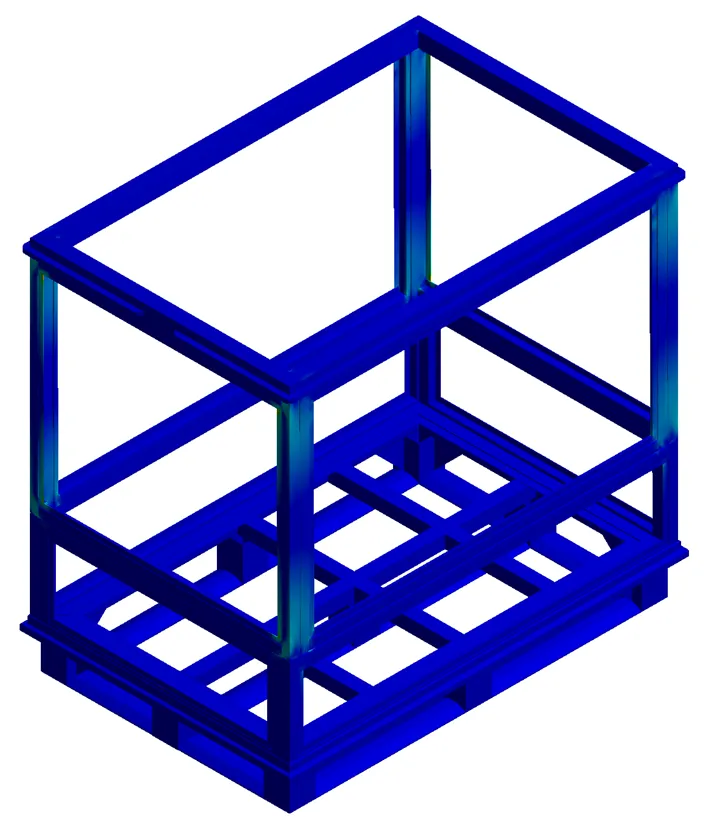
图6 优化后屈曲稳态分析

3 结语

以周转铝箱作为研究对象，基于屈曲强度失效和稳定失效2个失效准则，进行了静力学分析和屈曲模态分析，并依据分析结果对周转铝箱进行了轻量化设计。通过对原方案的分析，周转铝箱的安全系数为6.98，安全余量较大，也说明轻量化空间较大。根据屈曲分析结果，箱体底部及侧柱呈现较好的结构强度，存在较大的轻量化空间，因此基于正交试验的方法对其进行优化设计。

采用4因素3水平建立正交表9(43)来进行试验，最终确定了9个设计方案。通过更新基础设计模型，借助有限元分析软件，对所获取的9个方案分别进行了静力分析，对获得结果进行极差分析，以箱体自身质量为唯一指标，确定了周转铝箱箱体侧柱厚度尺寸对箱体自身质量的影响最大，根据获得的因素影响顺序，建立回归方程并根据统计学进行可靠性检验，再采用Matlab求得了数学模型的最优解，优化后的方案自身质量降幅达到9.88%，并且通过分析验证其满足2个失效准则，轻量化效果显著。

[1] 白治明. 金属包装箱动力学分析及结构优化[D]. 西安: 陕西科技大学, 2019: 2-8.

Bai Zhi-ming. Dynamic Analysis and Structural Optimization of Metal Packaging Box[D]. Xi'an: Shanxi University of Science and Technology, 2019: 2-8.

[2] IAI. 预计到2050年铝需求将增长约80%再生铝可以满足一半的需求[J]. 铝加工, 2021(5): 45.

IAI. Aluminum Demand is Expected to Grow by about 80% by 2050. Recycled Aluminum can Meet Half of the Demand[J]. Aluminum Processing, 2021(5): 45.

[3] 唐远景. 我国铝及铝合金的应用及趋势浅析[J]. 轻金属, 1994(5): 61-64.

Tang Yuan-jing. Application and Trend Analysis of Aluminum and Aluminum Alloy in My Country[J]. Light Metals, 1994(5): 61-64.

[4] FENG Jun-jie, YIN Guan-sheng, TUO Hong-liang, et al. Parameter Optimization and Regression Analysis for Multi-index of Hybrid Fiber-Reinforced Recycled Coarse Aggregate Concrete Using Orthogonal Experimental Design[J]. Construction and Building Materials, 2021(267): 1-14.

[5] 李志强, 樊博, 张素风. 基于正交试验和有限元法的木支撑结构优化设计[J]. 包装工程, 2019, 40(19): 109-114.

LI Zhi-qiang, FAN Bo, ZHANG Su-feng. Optimal Design of Wood Support Structure Based on Orthogonal Test and Finite Element Method[J]. Packaging Engineering, 2019, 40(19): 109-114.

[6] 邱自学, 鞠家全, 任东, 等. 基于正交试验、组合赋权–灰色关联的机床横梁优化设计[J]. 振动与冲击, 2017, 36(12): 105-111.

QIU Zi-xue, JU Jia-quan, REN Dong, et al. Optimal Design of Machine Tool Beam Based on Orthogonal Test, Combination Weighting-Gray Correlation[J]. Vibration and Shock, 2017, 36(12): 105-111.

[7] 高志来, 邱自学, 任东, 等. 基于正交试验法的龙门铣床滑枕多目标优选设计[J]. 现代制造工程, 2019(5): 97-103.

GAO Zhi-lai, QIU Zi-xue, REN Dong, et al. Multi-Objective Optimization Design of Gantry Milling Machine Ram Based on Orthogonal Test Method[J]. Modern Manufacturing Engineering, 2019(5): 97-103.

[8] 鞠家全, 邱自学, 崔德友, 等. 基于正交试验的机床移动横梁多目标优化设计[J]. 机械强度, 2018, 40(2): 356-362.

JU Jia-quan, QIU Zi-xue, CUI De-you, et al. Multi-Objective Optimization Design of Machine Tool Moving Beam Based on Orthogonal Test[J]. Mechanical Strength, 2018, 40(2): 356-362.

[9] 杨思瑞, 白海清, 李超凡, 等. 镍基高温合金激光熔覆数值模拟及回归正交试验优化[J]. 激光与光电子学进展, 2022, 59(13): 1-13.

YANG Si-rui, BAI Hai-qing, LI Chao-fan, et al. Numerical Simulation of Nickel-Based Superalloy Laser Cladding and Optimization of Regression Orthogonal Experiment[J]. Advances in Laser and Optoelectronics, 2022, 59(13): 1-13.

[10] WU Yi-fei, ZHAO Hong-xia. Optimization Analysis of Structure Parameters of Steam Ejector Based on CFD and Orthogonal Test[J]. Energy, 2018, 151: 79-93.

[11] GB/T 228.1—2010, 金属材料拉伸试验第1部分：室温试验方法[S].

GB/T 228.1—2010, Tensile Test of Metallic Materials Part 1: Room Temperature Test Method [S].

[12] 雍兆铭, 刘宝庆, 戴林富, 等. 搪玻璃设备许用应力的探讨[J]. 压力容器, 2012, 29(11): 30-33.

YONG Zhao-ming, LIU Bao-qing, DAI Lin-fu, et al. Discussion on Allowable Stress of Glass-Lined Equipment[J]. Pressure Vessel, 2012, 29(11): 30-33.

[13] 滑广军, 易颖茵, 肖建, 等. 基于Ansys的重型包装钢架箱工程轻量化设计[J]. 包装工程, 2022, 43(3): 183-188.

HUA Guang-jun, YI Ying-yin, XIAO Jian, et al. Lightweight Design of Heavy-Duty Packaging Steel Frame Box Engineering Based on ANSYS[J]. packaging engineering, 2022, 43(3): 183-188.

[14] LIAO Min-he, JIN Ri-tian, REN Hao-wei, et al. Orthogonal Experimental Design for the Optimization of Four Additives in a Model Liquid Infant Formula to Improve its Thermal Stability[J]. LWT, 2022(163): 3-5.

[15] 李云雁, 胡传荣. 试验设计与数据处理[M]. 北京: 化学工业出版社, 2017: 104-136.

LI Yun-yan, HU Chuan-rong. Experimental Design and Data Processing[M]. Beijing: Chemical Industry Press, 2017: 104-136.

[16] 李琛, 牛美亮, 赵玉松. 钢化玻璃运输包装设计与有限元分析[J]. 包装工程, 2018, 39(15): 113-118.

LI Chen, NIU Mei-liang, ZHAO Yu-song. Tempered Glass Transportation Packaging Designand Finite Element Analysis[J]. Packaging Engineering, 2018, 39(15): 113-118.

Lightweight Design of Aluminum Turnover Box

DENG Yu-lin1, LI Guang1, CAO Fei2

(1. School of Light Industry Science and Engineering, Tianjin University of Science and Technology, Tianjin 300457, China; 2. College of Packaging and Printing Engineering, Tianjin Vocational Institute, Tianjin 300410, China)

The work aims to take aluminum turnover boxes as research objects to conduct lightweight design of aluminum turnover boxes through finite element analysis and orthogonal experimental design to solve the problem of excess structural strength design. The stacking condition of aluminum turnover boxes was simulated and analyzed with the finite element analysis software Ansys Workbench. The findings were assessed with two failure criteria. The optimization scheme was designed based on orthogonal test. The mathematical model of the optimization scheme was built and calculated with Matlab. According to the simulation analysis, the first-order modal load factor was 6.98. The aluminum turnover box had a substantial safety margin based on the failure criterion. According to the range analysis, with self-weight of the box as the only indicator, it was determined that the thickness of the side column of the aluminum turnover box had the biggest effects on the self-weight of the box. Then, according to the mathematical model of the optimization scheme built and calculated with Matlab, the lightweight scheme decreased the self-weight by 9.88% at the mean time of meeting the working conditions. The aluminum turnover boxes of lightweight design meet the two criteria of strength failure and stable failure, as well as the actual operating conditions. It also demonstrates that the scheme of utilizing the orthogonal test approach and finite element analysis for lightweight design is feasible. It decreases the costs and increases the utilization rate of materials.

aluminum turnover box; lightweight; orthogonal test; finite element

TB482.2

A

1001-3563(2023)01-0272-07

10.19554/j.cnki.1001-3563.2023.01.031

2022−05−30

天津市科技计划（21YDTPJC00420）

邓昱琳（1997—），女，硕士生，主攻物流运输包装设计。

李光（1975—），男，博士，副教授，主要研究方向为包装机械与虚拟仿真。

责任编辑：曾钰婵