基于改进型自抗扰控制的永磁同步电机伺服控制

金爱娟，丁哲琪，李少龙，张豪，姜骁恩

基于改进型自抗扰控制的永磁同步电机伺服控制

金爱娟，丁哲琪，李少龙，张豪，姜骁恩

（上海理工大学，上海 200093）

解决传统包装机械存在的包装速度慢、包装质量堪忧等问题，满足包装机械的高效率、高精度等要求，提高食品包装的自动化水平和包装企业的经济效益。对具有较大潜力的永磁同步电机，进行控制器和控制方法的研究与改进，并最终选定自抗扰控制器，对自抗扰控制器中非光滑函数fal进行改进得到连续平滑的tal函数，使其减小在原点周围的颤振，并且基于tal函数重新设计非线性状态误差反馈率和扩张状态观测器，以取得对永磁同步电机更好的控制效果。仿真表明，tal函数比fal函数具有更好的平滑性和连续性。基于改进型自抗扰控制的永磁同步电机具有更好的动态性能、稳态精度、抗扰能力和跟踪能力。文中优化后的永磁同步电机伺服控制系统，适用于高精度、负载变动频繁的场合，能够有效地提高包装自动化水平，满足高效率、高精度的包装行业要求。

包装机械；永磁同步电机；自抗扰控制；非线性函数

随着工业的快速发展，人工成本也越来越高，包装行业通过不断引进全自动化生产线来替代人工，从而降低企业成本[1]。为了提高食品包装的自动化水平，需要对控制器、控制方法、传感器和驱动方法进行全面的研究，根据当前的技术发展水平，对食品包装机械自动化的发展方向进行探讨和分析，通过这样食品包装机械的自动化水平才能真正的提高，保证食品包装机械运行的可靠性和稳定性，提高食品包装机械企业的经济效益[2]。目前，食品行业对包装机械的要求主要是生产效率性、灵活性、稳定性、可靠性和环保性。在自动化包装流水线中，永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）具有较大的潜力，成为了高精度、高效率传动装置的主驱动电机。永磁同步电机具有体积小、效率高、功率密度高等优点，被广泛应用于在包装机械、数控机床以及飞行器等高性能、高精度伺服驱动场合[3-4]。

一个好的控制方式往往能决定永磁同步电机的性能，目前比较常见的控制方式有比例–积分–微分控制（Proportion Integration Differentiation，PID）、自适应控制、滑膜控制、反步法控制、自抗扰控制等[5-6]。在实际电机控制系统中，PID控制器仍然占主要地位，但是“基于误差反馈消除误差”的机理，存在着快速性和超调之间的矛盾。此外，PID控制的抗干扰能力、跟踪性能也较弱[7]。

针对PID控制器的不足，中科院韩京清教授[8]于1998年提出了自抗扰控制（Active Disturbance Rejection Control，ADRC）。ADRC将所有的不确定性和非线性，包括参数变化、未建模动态、外部未知干扰等，统称为总扰动，并由扩张观测器来估计并给予补偿，因此在自抗扰控制器框架下，精确模型是不必要的，控制器本身具有较强的抗干扰能力和鲁棒性。近年来，国内外一些学者研究了自抗扰控制器的性能，比如绝对稳定性证明[9]。陈志旺等[10]对扩张状态观测器的收敛性进行了分析，并将ADRC技术运用到了四旋翼姿态控制中来。Castaneda等[11]利用ADRC解决了机器人在不确定动力学模型下的轨迹跟踪问题。王怡怡等[12]利用扩张状态观测器和非线性反馈控制律，提高控制品质，实现了无人直升机在受噪声干扰下的稳定性和高控制精度。这些研究都是基于原有的非线性函数fal进行设计的，但fal函数在分段点处不光滑，容易产生高频颤振。很多学者针对这一问题提出了一系列的解决方案，周涛[13]用反双曲正弦函数来替代fal函数，能较好地抑制微分峰值；杨淑英等[14]设计了一种增益连续非线性校正函数fac，该函数具有统一的表达式，不存在分段点，使扩张状态观测器具有较强的参数鲁棒性；蒲明等[15]对fal函数进行了改进并重新设计了3种扩张状态观测器，有效地减小了被控状态的总误差。

受上述研究启发，为使PMSM具有更好的动态特性、抗扰能力和跟踪能力，更好地满足包装机械高效率、高稳定性和高精度等要求。文中提出一种改进型自抗扰控制的方法，构建新的非线性函数tal。在原有fal函数的基础上，基于等价无穷小的概念，用三角函数和多项式拟合，解决分段点处不光滑的问题，减小原点附近的高频颤振；此外，为使自抗扰控制更加符合“小误差大增益，大误差小增益”特性，在误差较大时进行了再次改进，提高系统的抗干扰能力。

1 永磁同步电机数学模型

文中研究对象是表贴式永磁同步电动机，数学模型包括电压方程、磁链方程、电磁转矩方程和机械方程[16]。在–同步旋转坐标系下的数学模型为：

式中：u、i、u、i分别为–轴的电压和电流；s为定子电阻；L、L为–轴的电感分量；e为电角速度；f为机械角速度；ψ、ψ为定子磁链的–轴分量；f为永磁体磁链；n为极对数；为转子的转动惯量；为阻尼系数；e为电磁转矩；L为负载转矩。

2 改进型自抗扰控制器设计

自抗扰技术是一种不依赖系统模型特征，主动对系统进行扰动抑制的先进控制技术。自抗扰控制器主要由跟踪–微分器（Tracking Differentiator, TD）、扩张状态观测器（Extended Stata Observer, ESO）以及非线性状态误差反馈控制律（Nonlinear Stata Error Feedback, NLSEF）[17]3部分构成，其基本结构见图1。

2.1 自抗扰控制器结构

1）跟踪–微分器（TD）。经典微分器对噪声具有放大效应，TD能有效地减弱噪声的放大效应，较好地解决从伴随着噪声的量测信号中提取信号和信号的微分。同时，TD给系统输入安排了过渡过程，扩大比例因子和微分因子的选取范围[18]，缩小零初始条件下的误差，提高系统的响应时间。TD表达式为：

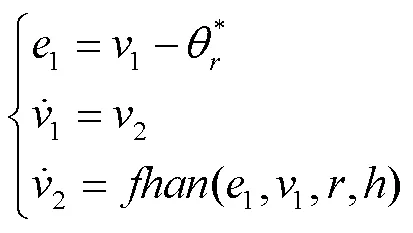
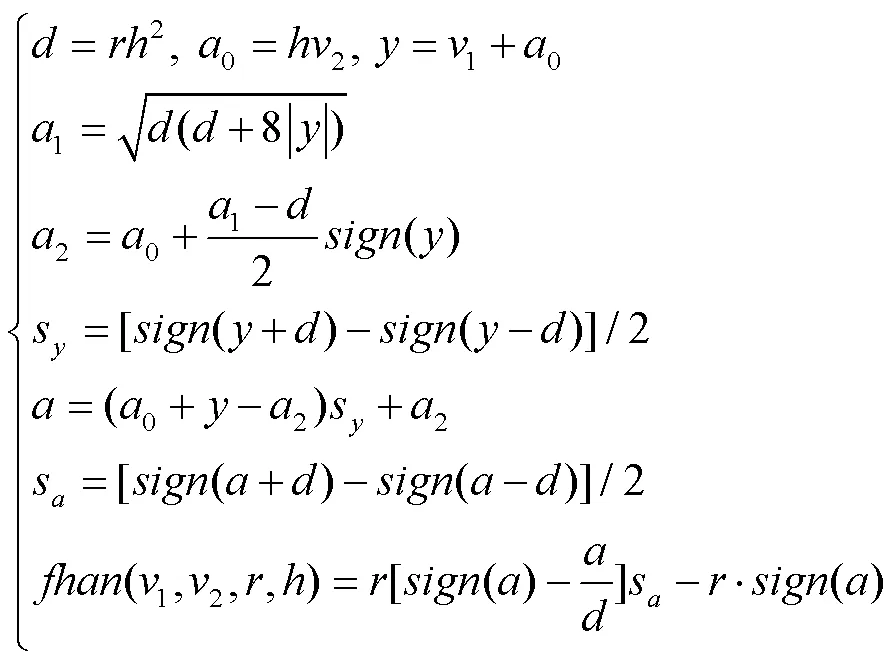
2）扩张状态观测器（ESO）。ESO是自抗扰控制器中最核心的组成部分，其作用是解决主动抗扰中扰动观测这一问题。其本质是将所有不确定、非线性的扰动确定化、线性化，扩展为一个新的状态变量，使系统转化为简单的“积分串联型”，再利用ESO进行实时观测并补偿抵消，以此提升系统的性能。ESO不依赖于所生成的扰动模型，也不需要直接量测来观测扰动并获得估计值，其表达式为：

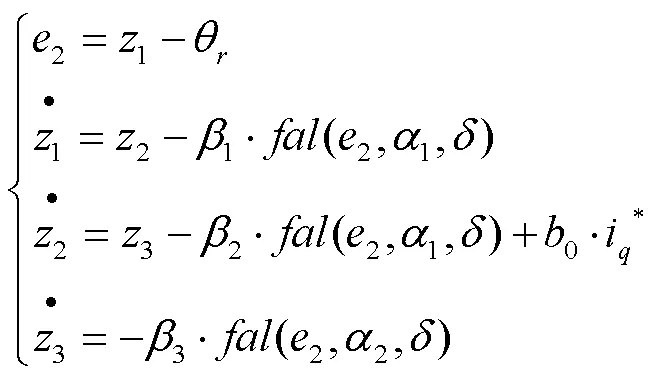
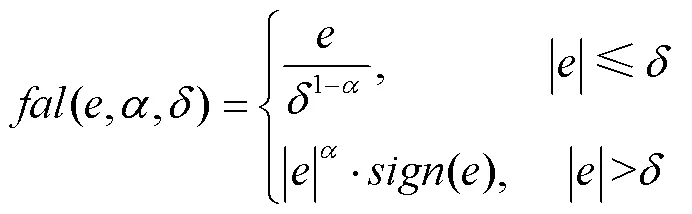
3）非线性状态误差反馈控制率（NLSEF）。NLSEF是基于TD和ESO状态变量估计之间的误差非线性算法控制器。ESO和NLSEF总扰动的补偿量构成了系统的控制量，提高了系统控制性能，也实现了动态补偿，其表达式为：

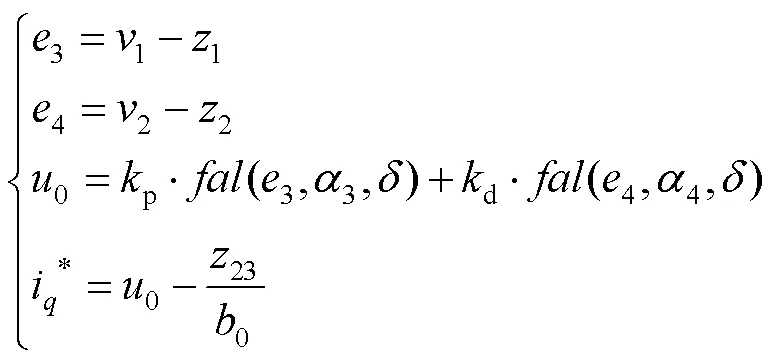
式中：p、d分别为误差的比例因子和微分因子。

2.2 改进型ESO设计

ESO的核心部分是非线性函数。目前，传统ADRC中的非线性函数是fal函数，由式（5）、式（7）和式（8）可知，fal函数连续，但在分段点−和处存在不可导情况，缺乏光滑性和连续性。在实际系统中，若取值过小，在原点附近容易产生颤振，降低系统的鲁棒性。

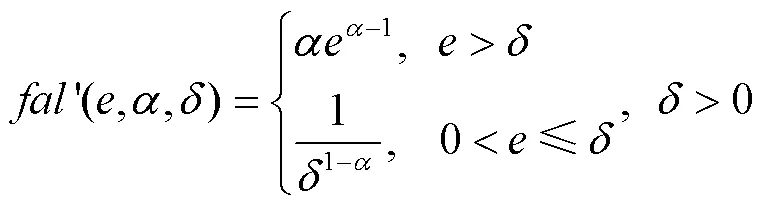
为了上述解决问题，需要在fal函数的基础上设计一个连续光滑的非线性函数tal函数，从而提高扩张观测器的性能。

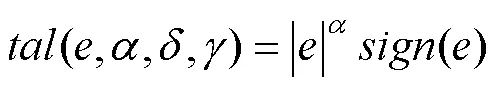
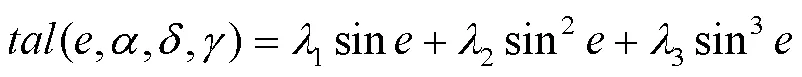
基于等价无穷小的概念，选用三角函数拟合而非指数函数多项式拟合，是因为sin、sin2以及sin3比指数函数在原点附近的平滑性更好。

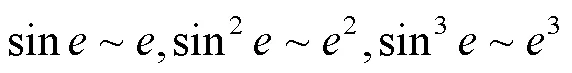
为了满足分段函数在定义域内连续，分段点处可导的条件，则式（12）成立。

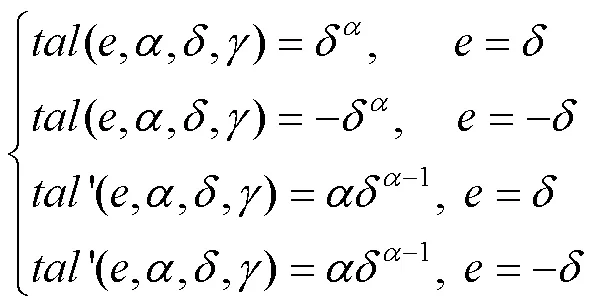
求解可得：

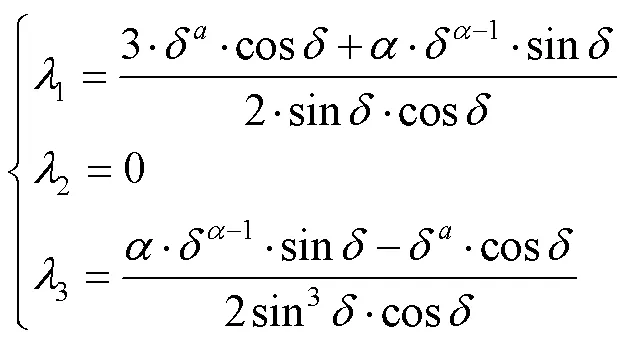
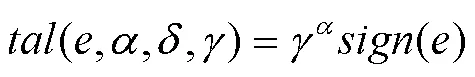
那么，最后完整的tal函数形式如下：

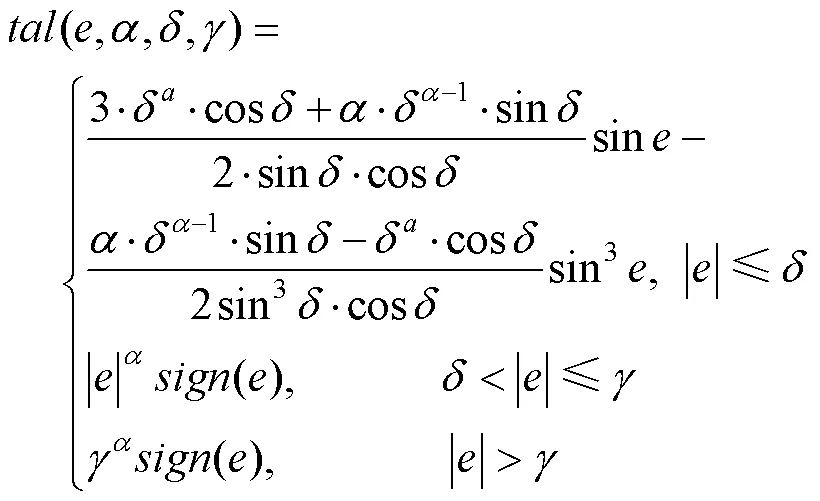
为了验证非线性函数fal函数和tal函数的性能，取=0.25、=0.25、=1进行Matlab仿真实验。tal函数与fal函数的特性曲线见图2；tal函数与fal函数的误差增益曲线见图3。

图2 函数特性曲线

Fig.2 Function characteristic curve

由图2可以看出，fal函数在分段点处有明显的转折，而tal函数在原点周围具有更好的连续性和平滑性；由图3可以看到，当输出误差趋近于0时，tal函数的输出增益明显大于fal函数，而当输出误差较大时，tal函数的输出增益则略小于fal函数。由此，可以得出以下几点结论。

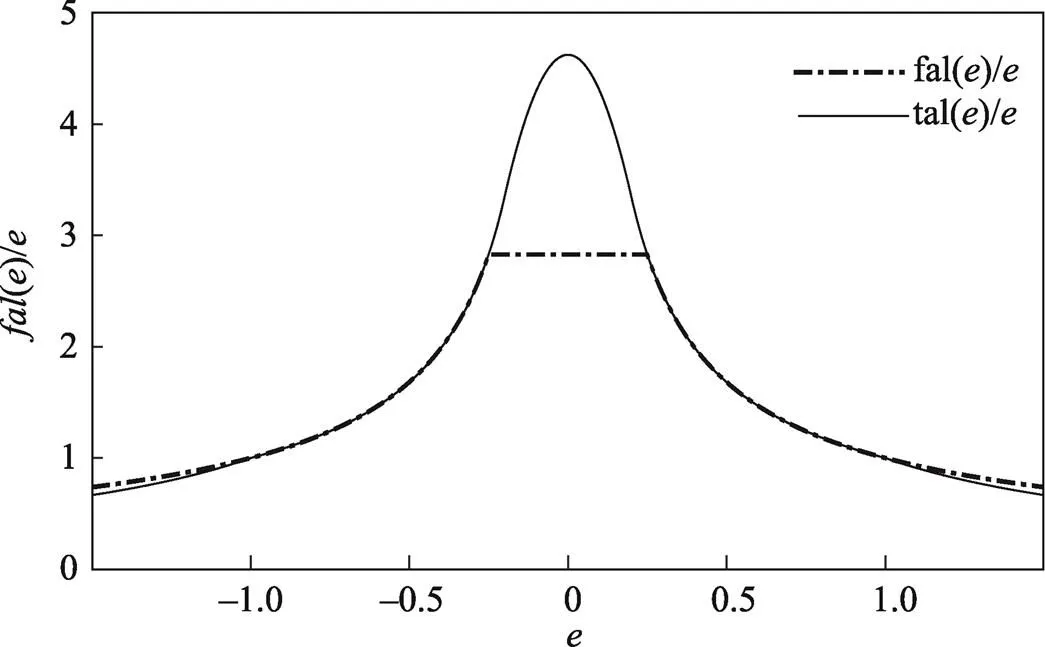
图3 误差增益曲线

1）与fal函数相比，tal函数能有效地减小在原点周围存在的高频颤振。

2）tal函数更能体现“小误差大增益，大误差小增益”的机理。误差较小时采用大增益，增加系统的快速性；误差较大时采用小增益，减小超调，调和了快速性和超调的矛盾。

3）基于tal函数的改进型ESO在跟踪系统状态1、2、3时不会存在较大的偏离，提高了观测器的精度，也提高了系统的抗干扰能力。

2.3 改进型ESO的收敛条件

用tal函数代替fal函数，得到的改进型ESO表达式为：

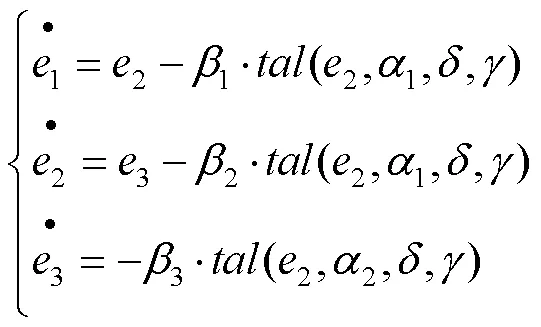
式（17）可以写成：

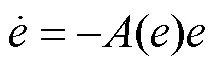
其中：

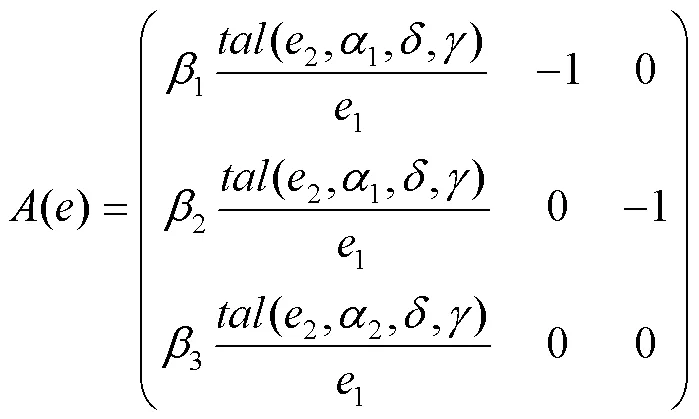
引理1[20]：若存在矩阵

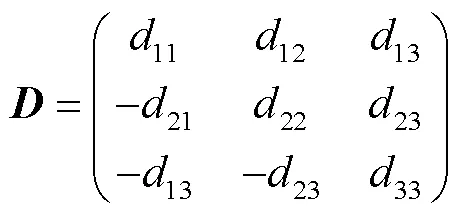
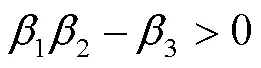
2.4 改进型NLSEF设计

NLSEF类似于传统的PID控制器，又不同于PID控制器，传统PID控制器是采用线性叠加的方式来处理误差，而NLSEF是对误差进行非线性计算。改进型NLSEF将引入积分因子和误差的积分，对通过TD转换得到的误差、误差的积分和误差的微分进行非线性计算，消除稳态误差，进一步提高系统的控制精度，增强系统的鲁棒性。改进型NLSEF表达式见式（21）。

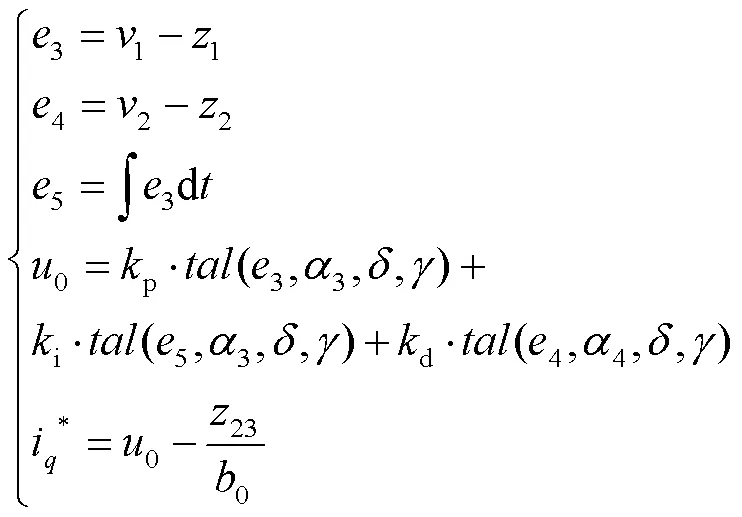
3 仿真实验与分析

相较于典型的分布式位置伺服控制系统，位置环、转速环、电流环的三环设计模式，文中将转速环、位置环合并在一起，构成转速位置环，并采用改进型ADRC进行控制，电流环则依旧采用传统PID作为控制方式。具体的改进型ADRC的PMSM伺服系统控制框图见图4。

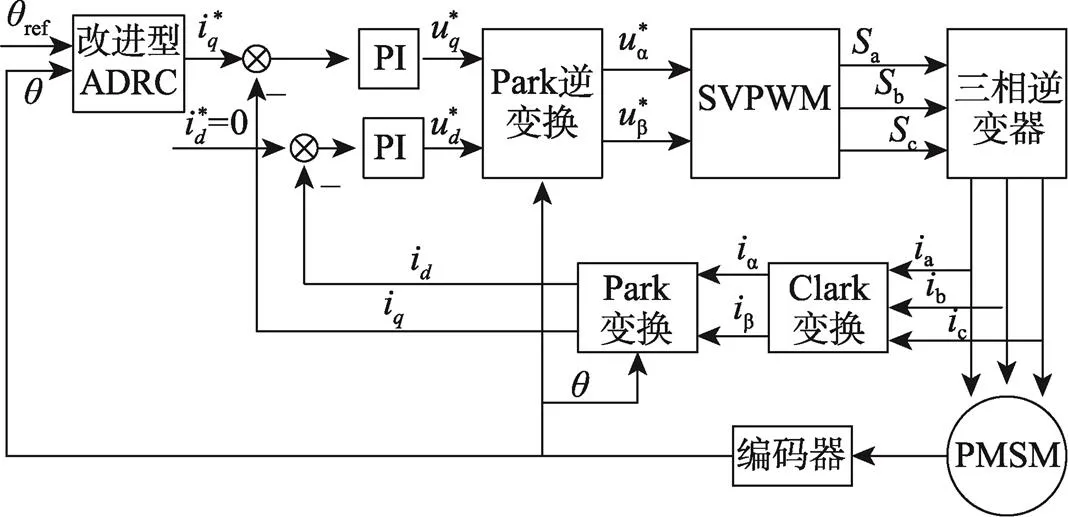
图4 改进型ADRC的PMSM伺服系统控制框图

在实际工作过程中，PMSM伺服包装控制系统有时会频繁变动位置，因此文中设计了空载变位置实验，验证系统的动态特性；也会因为温度过高，车间粉尘多等恶劣工况，产生摩擦力矩，导致负载变化，文中针对这一情况设计了变载实验，验证系统的抗扰特性；PMSM伺服包装控制系统也会存在跟踪某一工件的情况，例如机械臂，因此文中设计了跟踪正弦信号的跟踪实验，验证系统的跟踪精度。为了增加实验的可靠性，文中将选取PID控制器、传统ADRC控制器、基于指数函数改进非线性函数的ADRC控制器（E–ADRC）[21]和I–ADRC作为对比，进行实验。根据图4，在Matlab/Simulink环境中搭建仿真模型，永磁同步电机相关参数见表1。

ADRC控制器参数较多，其参数整定相对烦琐，通常采用智能算法进行整定，但每个控制器模块又是相互独立的，可以分开进行参数整定，经过多次调试，最终所得改进型ADRC参数见表2。

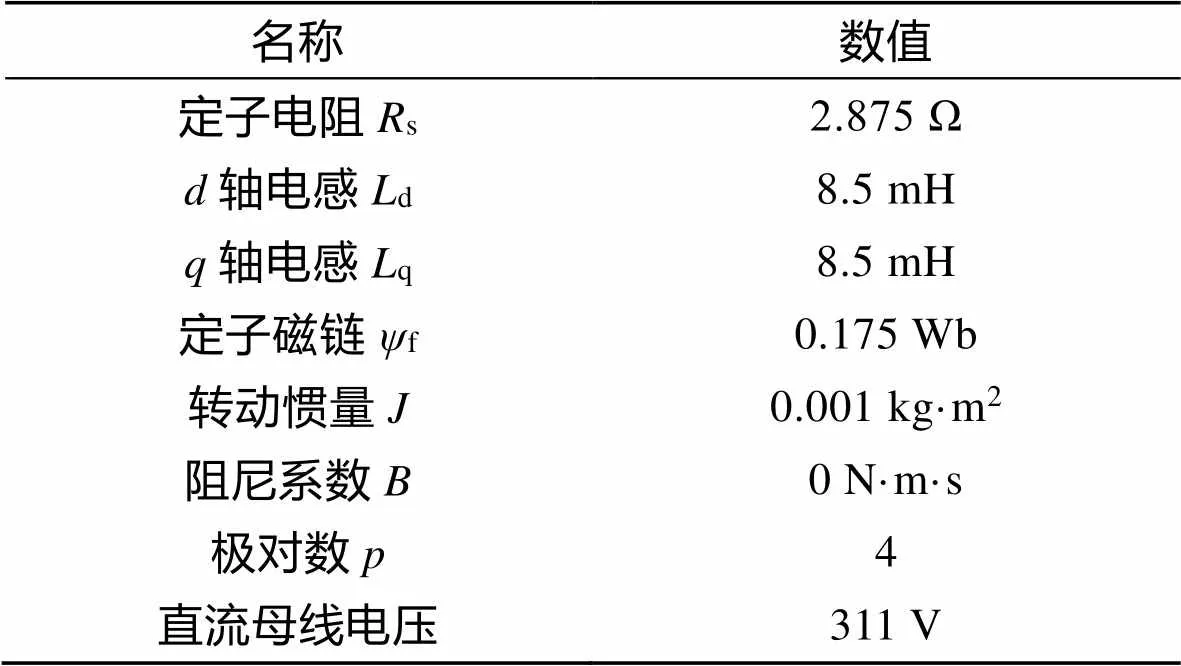
表1 永磁同步电机参数

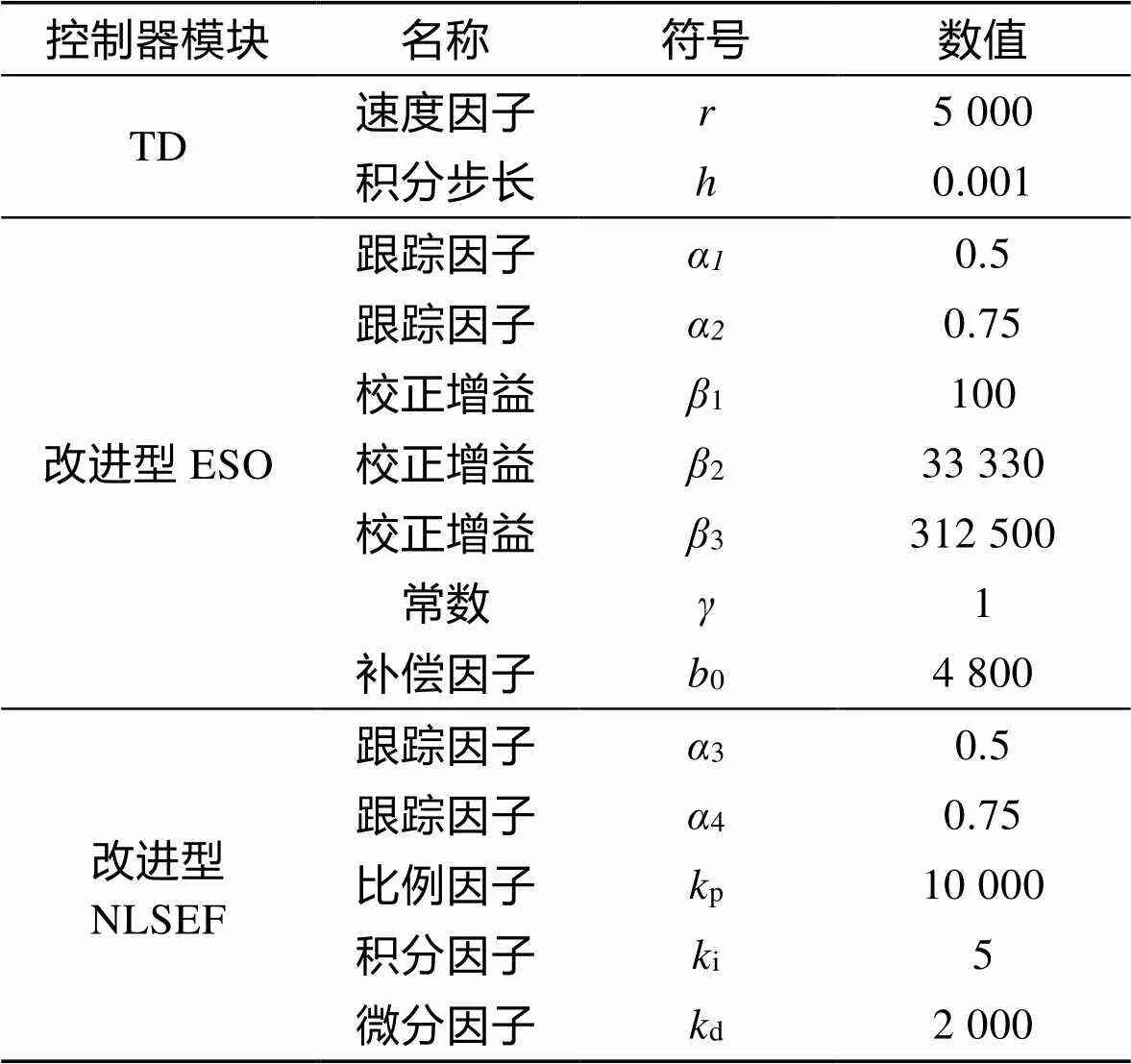
表2 改进型ADRC参数

3.1 空载变位置实验——动态特性

在空载变位置实验中，电机转子给定位置角初始值为5 rad空载启动，在0.2 s时给定位置角突变至1 rad，在0.4 s时突变至3 rad。仿真结果见图5，整理数据见表3。

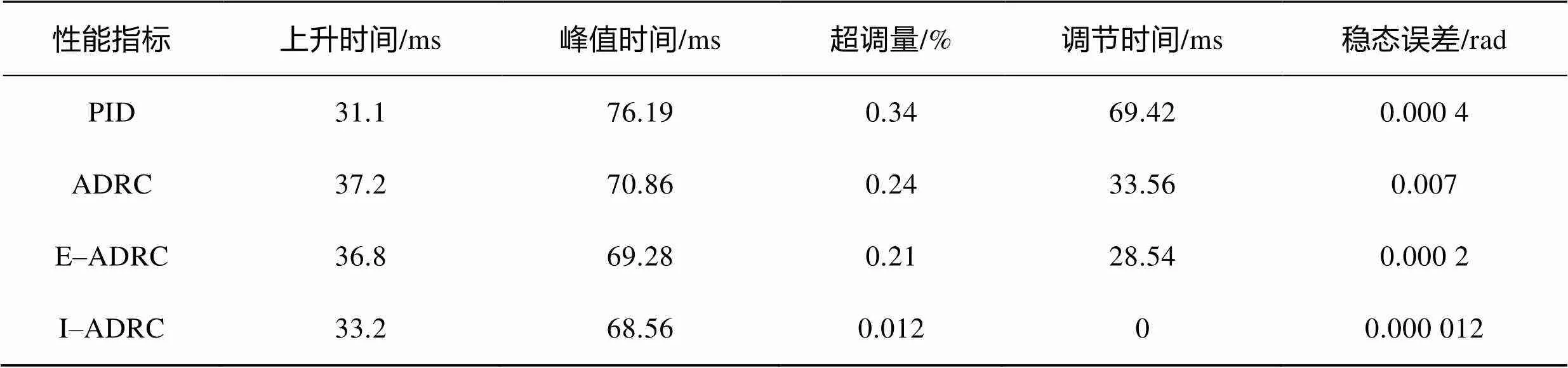
表3 空载变位置实验电机性能指标

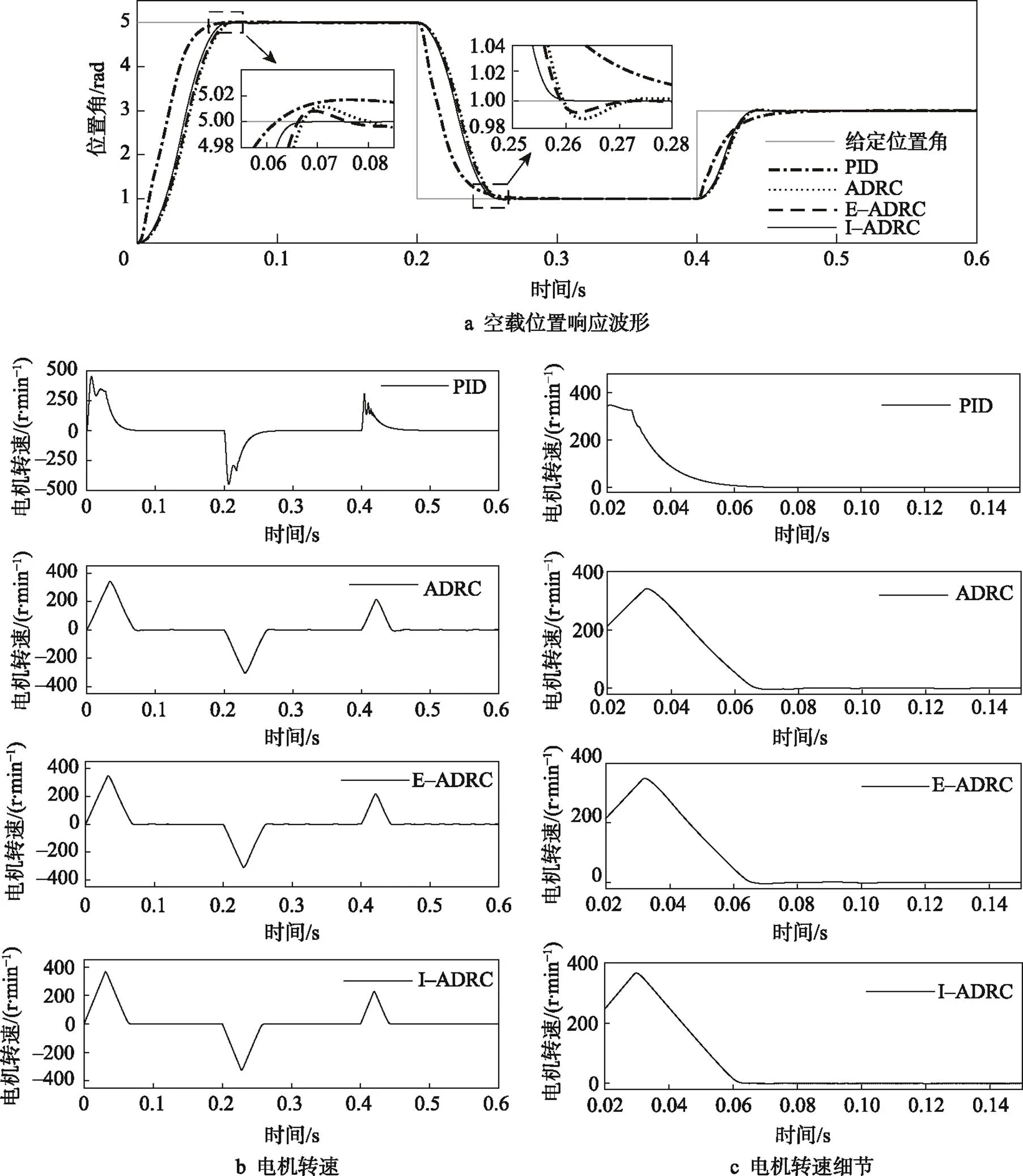
图5 空载变位置实验波形

通过表3、图5a和图5b可知，在快速性方面，传统PID控制的上升时间最短为31.1 ms，比I–ADRC快了2.1 ms，这是由于ADRC存在TD安排过渡过程，加速度小于电机所能达到的最大加速度；在接近给定角度时，PID控制的上升速度明显减慢，而ADRC的上升速度相对平稳，其原因是“小误差大增益”，在误差较小时有较大的输出，使其保持良好的动态特性。在阻尼特性方面，I–ADRC的超调量为0.012%，比PID控制缩小了0.328%；传统ADRC的超调量为0.24%，比PID控制缩小了0.10%，由此可以说明ADRC控制器很好地调和了快速性与超调之间的矛盾。在文中调节时间选取的是稳态值的±0.2%，I–ADRC的超调始终没有超过0.2%，因此调节时间为0 ms，优于其他控制方式。由表3和图5a分析可得，传统ADRC的稳态误差为0.007 rad，远大于其他几种控制方式，这是由于fal函数不可导，曲线不够光滑，因而容易产生高频颤振，改进fal函数的I–ADRC的稳态误差为0.000 012 rad，远小于PID控制和E–ADRC控制。单独观察图5a分析可知，在变角度时，I–ADRC控制能保持原有的动态性能；而PID控制的上升时间变长，超调变小，与给定位置角度5 rad时的动态性能相比相差较大，因此，I–ADRC与其他控制方式相比，具有更好的动态特性和稳态精度。在实际工作过程中，当包装机械频繁变动位置时，采用I–ADRC的包装机械能够快速地完成工作，也不会因为系统位置变动频繁产生较大的误差，在保证良好的鲁棒性前提下，满足包装机械的精度要求。

3.2 变载实验——抗扰特性

在变载实验中，电机转子给定角度初始值为5 rad空载启动，在0.2 s时将负载突增至5 N·m，在0.4 s时负载突减5 N·m。仿真结果见图6，整理数据见表4。

通过表4、图6a和图6b可知，在负载突增时，ADRC的角度突变峰值和转速突变峰值远小于传统PID控制，其中I–ADRC的角度突变峰值和转速突变峰值小于E–ADRC和传统ADRC。如果用角度超调量表示就显得更加直观，I–ADRC的角度超调量为0.11%，比E–ADRC的小了0.14%，比传统ADRC的缩小了0.38%，比PID控制的足足缩小了2.21%。观察表4、图6a和图6d可得，由于PID的突变较大，恢复时间远远大于ADRC，I–ADRC的恢复时间最短；在稳态性能方面，PID控制的稳态误差为0.000 8 rad，小于I–ADRC的0.001 6 rad和传统ADRC的0.007 3 rad，说明PID控制相较于ADRC在稳态精度上有优势。观察图6b、图6c可以发现，当突加负载时，PID控制的转速发生了明显的变化，而I–ADRC的转速变化相对较小，几乎可以忽略，具有极强的抗扰能力。观察图6a和图6e在负载突减时，情况与负载突增时相类似，只是角度突变峰值、超调量、恢复时间和稳态误差相较于负载突增时，整体都小一些。综合比较表4中的各个因素，I–ADRC控制比其他几种控制方法恢复时间更短，超调量更小，体现出更好的抗扰能力，适用于负载变动频繁的伺服系统。在实际的车间中，由于粉尘、温度等影响，包装机械往往会发生抖动，产生较大的噪声，导致控制精度降低，精确定位时间加长。改进的包装机械突变峰值较低，稳态误差较小，恢复时间短，因此其抖动程度和噪声较小，精确定位时间较短，系统更趋于稳定，能有效避免意外事件的发生。

3.3 空载跟踪实验——跟踪特性

在空载跟踪实验中，以电机转子给定角为正弦输入θ=sin(10π1.5π)1启动，仿真结果见图7，整理数据见表5。

通过表5、图7b和图7c可知，在跟踪正弦信号时，PID控制存在明显的跟踪误差，这是由于跟踪正弦信号时，转速较低，只有62 r/min，PID控制器的输出较小，不足以充分激励电流内环，从而导致跟踪误差的产生。ADRC则具有更短的滞后时间，更小的幅值衰减，是因为ADRC依靠转速、位置的综合非线性控制，在低速时具有良好的位置调节功能，使得ADRC能够很好地跟踪正弦信号。其中，I–ADRC的滞后时间为1.953 ms，远远小于传统PID控制的16.7 ms，比次优的E–ADRC快了0.074 ms，转化成相位差，PID的相位差高达15°，而I–ADRC仅有1.758°。在幅值衰减方面，图7a能明显的看出PID控制的衰减，衰减比例达到了正弦波最大幅值的6.692%，在幅值衰减方面I–ADRC比其他2种控制方式具有一定的优势，因此I–ADRC具有高精度的跟踪性能。

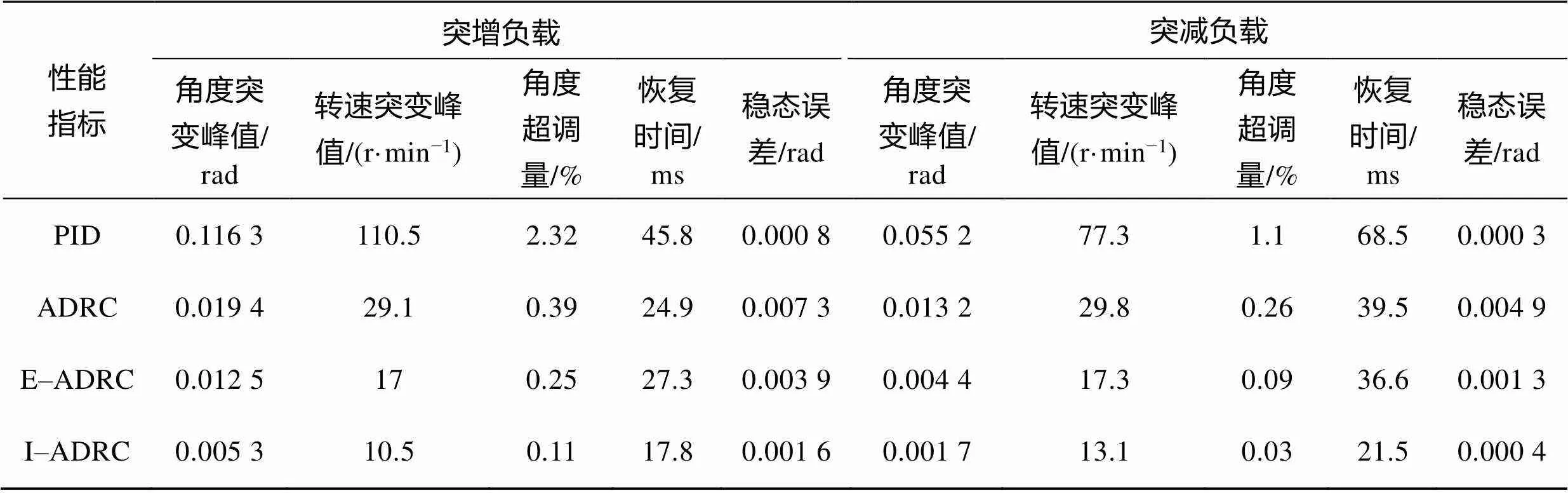
表4 变载实验电机性能指标

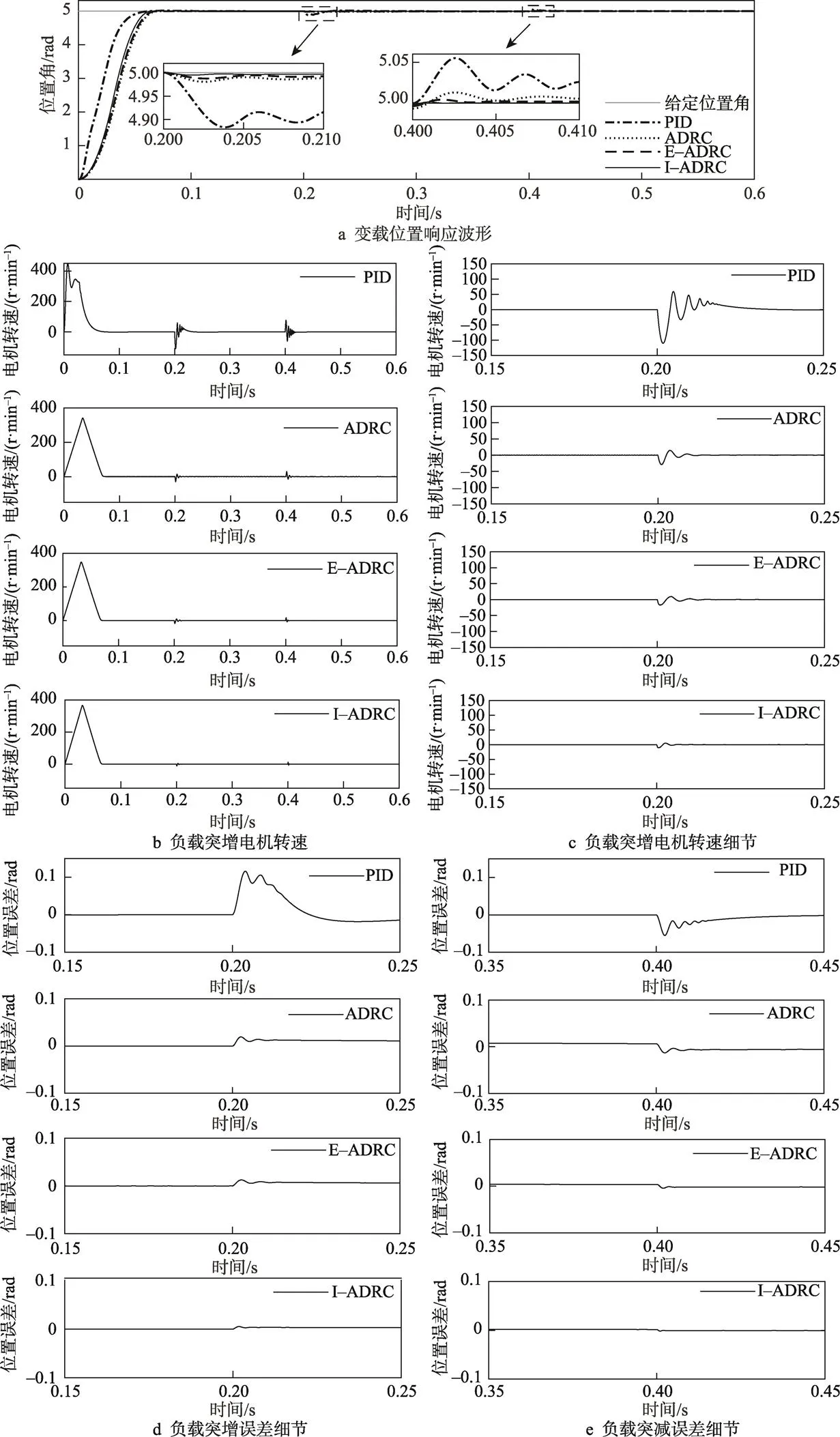
图6 变载实验波形

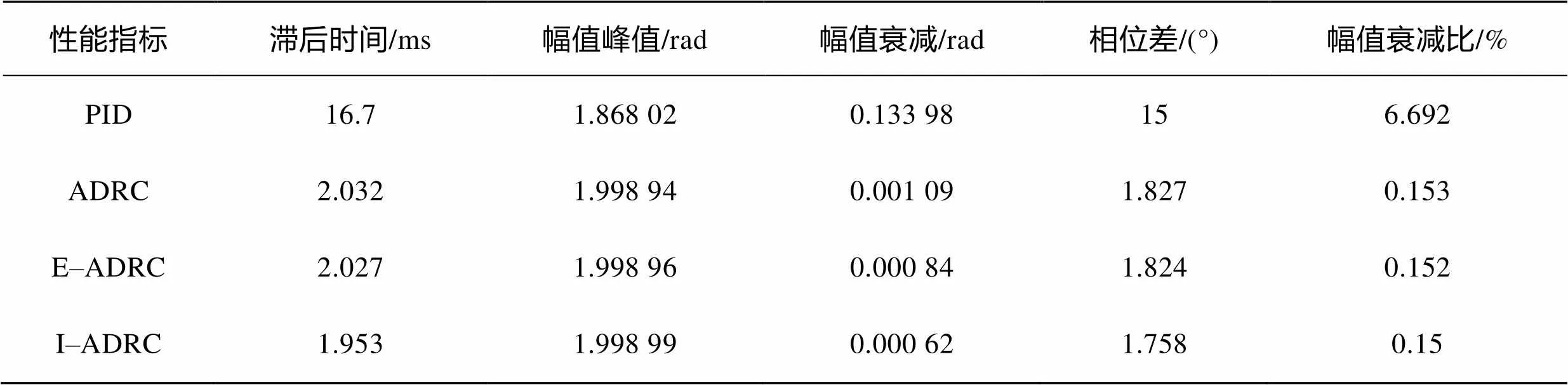
表5 空载跟踪实验电机性能指标

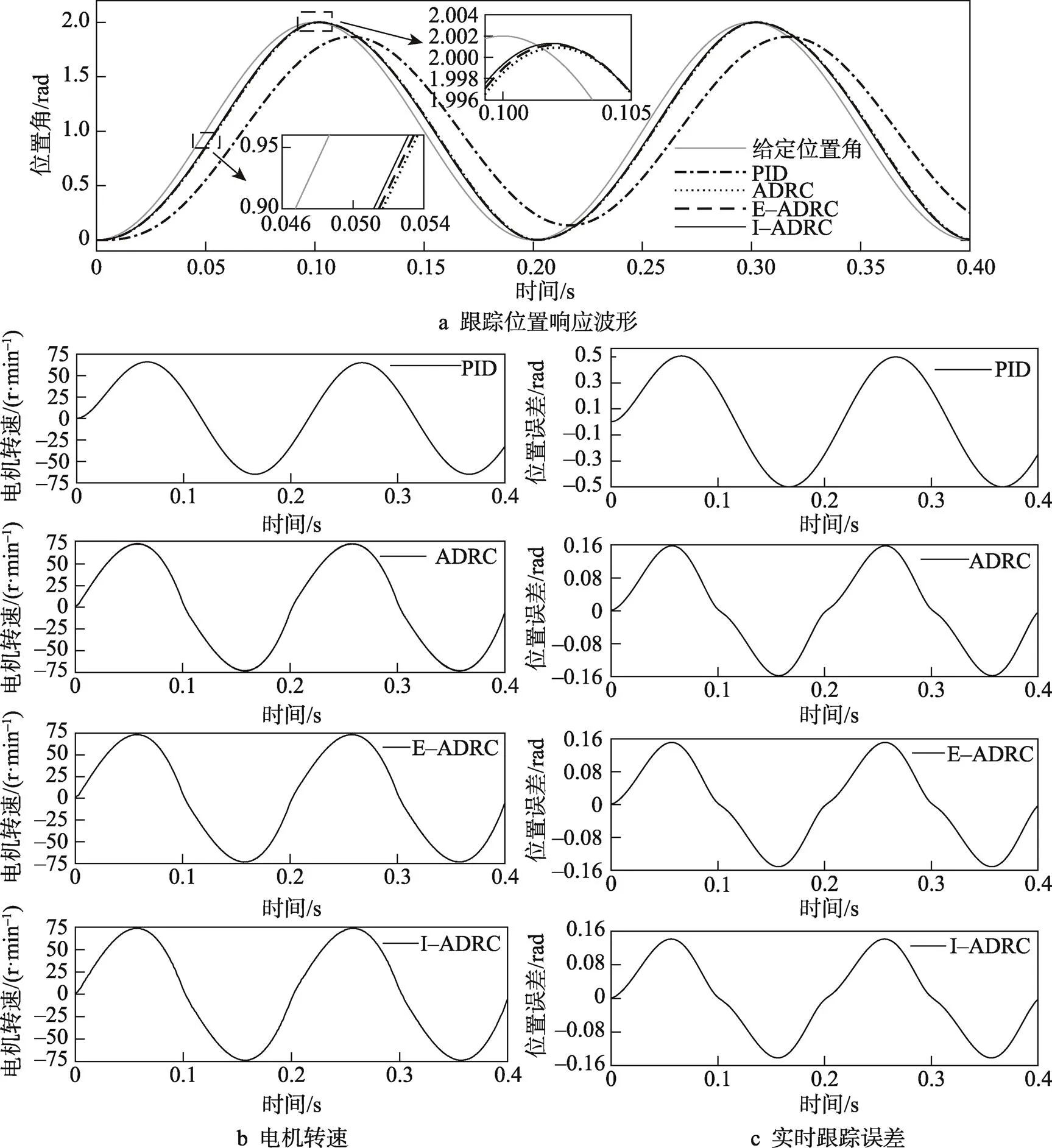
图7 空载跟踪实验波形

4 结语

文中遵循了“小误差大增益，大误差小增益”的原则，对非光滑函数fal进行改进，得到新的非线性函数tal，该函数具有很好的平滑性和连续性，有效地减小了在原点处的高频颤振；将积分项引入非线性状态误差反馈控制率中，提高了系统的稳态精度，并且由此构建改进型ADRC，并与传统PID控制、传统ADRC和E–ADRC做对比，进行了变位置、变载和跟踪实验。通过实验仿真数据可以得到，改进后的自抗扰控制器具有良好的动态特性、稳态精度、抗扰能力和跟踪特性。改进后的包装机械在复杂的工况下有效地提高了工作效率，产生较小的抖动和噪声，具有较高的控制精度；当应用到类似于机械臂的场合时，改进后的包装机械也具有较高的跟踪精度，符合包装行业对新型包装机械的要求。

[1] 刘新乐, 殷晓坤, 朱佳琪, 等. 基于伺服电机的上盖机控制系统设计[J]. 包装与食品机械, 2018, 36(4): 54-57.

LIU Xin-le, YIN Xiao-kun, ZHU Jia-qi, et al. Design of Control System for Capping Machine Based on Servo Motor[J]. Packaging and Food Machinery, 2018, 36(4): 54-57.

[2] DONG Tian-fei. Automatic Control of Food Packaging Machinery[C]// 6th International Conference on Advances in Energy Environment and Chemical Engineering, Electronic Network, 2020: 052067.

[3] 董家臣, 高钦和, 陈志翔, 等. 考虑电流环动态响应的永磁直线同步电机新型线性自抗扰控制[J]. 中国电机工程学报, 2019, 39(8): 2436-2448.

DONG Jia-chen, GAO Qin-he, CHEN Zhi-xiang, et al. New LADRC Design for Permanent Magnet Linear Synchronous Motor Considering Dynamic Response of Current Loop[J]. Proceedings of theCSEE, 2019, 39(8): 2436-2448.

[4] 聂川, 祝九思, 唐佳. 改善步进电机电流响应速度的抗饱和PI控制[J]. 包装工程, 2017, 38(17): 153-157.

NIE Chuan, ZHU Jiu-si, TANG Jia. Improvement of Anti-Windup PI Control of Current Response Speed for Stepping Motor[J]. Packaging Engineering, 2017, 38(17): 153-157.

[5] DENG Yong-ting, WANG Jian-li, LI Hong-wen, et al. Adaptive Sliding Mode Current Control with Sliding Mode Disturbance Observer for PMSM Drives[J]. ISA Transactions, 2019, 88: 113-126.

[6] ROMAN R C, PRECUP R E, PETRIU E M, et al. Combination of Data-Driven Active Disturbance Rejection and Takagi-Sugeno Fuzzy Control with Experimental Validation on Tower Crane Systems[J]. Energies, 2019, 12(8): 1-9.

[7] 孙斌, 王海霞, 苏涛, 等. 永磁同步电机调速系统非线性自抗扰控制器设计与参数整定[J]. 中国电机工程学报, 2020, 40(20): 6715-6725.

SUN Bin, WANG Hai-xia, SU Tao, et al. Nonlinear Active Disturbance Rejection Controller Designand Tuning for Permanent Magnet Synchronous Motor Speed Control System[J]. Proceedings of the CSEE, 2020, 40(20): 6715-6725.

[8] 韩京清. 自抗扰控制技术估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008: 134-136.

HAN Jing-qing. Active Disturbance Rejection Control Technique[M]. Beijing: National Defense Industry Press, 2008: 134-136.

[9] LI Jie, XIA Yuan-qing, QI Xiao-hui, et al. Absolute Stability Analysis of Non-Linear Active Disturbance Rejection Control for Single-Input-Single-Output Systems via the Circle Criterion Method[J]. IET Control Theory & Applications, 2015, 9(15): 2320-2329.

[10] 陈志旺, 张子振, 曹玉洁. 自抗扰fal函数改进及在四旋翼姿态控制中的应用[J]. 控制与决策, 2018, 33(10): 1901-1907.

CHEN Zhi-wang, ZHANG Zi-zhen, CAO Yu-jie. FalFunction Improvement of ADRC and Its Application in Quadrotor Aircraft Attitude Control[J]. Control and Decision, 2018, 33(10): 1901-1907.

[11] CASTANEDA L A, LUVIANO J A, CHAIREZ I. Robust Trajectory Tracking of A Delta Robot Through Adaptive Active Disturbance Rejection Control[J]. IEEE Transactions on Control Systems Technology, 2015, 23(4): 1387-1398.

[12] 王怡怡, 赵志良. 二自由度无人直升机的非线性自抗扰姿态控制[J]. 自动化学报, 2021, 47(8): 1951-1962.

WANG Yi-yi, ZHAO Zhi-liang. Nonlinear Active Disturbance Rejection Attitude Control of Two-DOF Unmanned Helicopter[J]. Acta Automatica Sinica, 2021, 47(8): 1951-1962.

[13] 周涛. 基于反双曲正弦函数的扩张状态观测器[J]. 控制与决策, 2015, 30(5): 943-946.

ZHOU Tao. Extended State Observer Based on Inverse Hyperbolic Sine Function[J]. Control and Decision, 2015, 30(5): 943-946.

[14] 杨淑英, 王玉柱, 储昭晗, 等. 基于增益连续扩张状态观测器的永磁同步电机电流解耦控制[J]. 中国电机工程学报, 2020, 40(6): 1985-1996.

YANG Shu-ying, WANG Yu-zhu, CHU Zhao-han, et al. Current Decoupling Control of PMSM Based on an Extended State Observer with Continuous Gains[J]. Proceedings of the CSEE, 2020, 40(6): 1985-1996.

[15] 蒲明, 刘鹏, 熊皑. Fal函数的改进及3种新型非线性扩张状态观测器[J]. 控制与决策, 2021, 36(7): 1655-1662.

PU Ming, LIU Peng, XIONG Ai. Advanced Fal Function and Three Novel Nonlinear Extended State Observers[J]. Control and Decision, 2021, 36(7): 1655-1662.

[16] YANG Jun, HUA Chenwen, LI Shi-hua, et al. Disturbance/Uncertainty Estimation and Attenuation Techniques in PMSM Drives—A Survey[J]. IEEE Transactions on Industrial Electronics, 2017, 64(4): 3273-3285.

[17] 朱斌. 自抗扰控制入门[M]. 北京: 北京航空航天大学出版社, 2017: 21-42.

ZHU Bin. Introduction to Active Disturbance Rejection Control[M]. Beijing: Beijing University of Aeronautics & Astronautics Press, 2017: 21-42.

[18] 闫桂林. 基于自抗扰四旋翼飞行器控制系统设计[D]. 镇江: 江苏科技大学, 2019: 34-40.

YAN Gui-lin. Control System Design of Quadrotor Aircraft Base on Active Disturbance Rejection[D]. Zhenjiang: Jiangsu University of Science and Technology, 2019: 34-40.

[19] 廖自力, 赵其进, 刘春光. 基于自抗扰技术的PMSM无位置传感器优化控制[J]. 微电机, 2018, 51(7): 44-47.

LIAO Zi-li, ZHAO Qi-jin, LIU Chun-guang. Sensorless Optimal Control for PMSM Based on Active Disturbance Rejection Control[J]. Micromotors, 2018, 52(7): 44-47.

[20] LOZGACHEV G I. On a Method of Construction of Lyapunov Function[J]. Autom Remote Control, 1998, 59: 1365-1368.

[21] 周啟航, 野邵文, 向政委, 等. 高超声速飞行器再入姿态改进自抗扰控制[J]. 计算机仿真, 2012, 29(12): 90-94.

ZHOU Qi-hang, YE Shao-wen, XIANG Zheng-wei, et al. Posture Improved Auto-Disturbance-Rejection Control for Hypersonic Missilein Reentry[J]. Computer Simulation, 2012, 29(12): 90-94.

Servo Control of PMSM Based on Improved ADRC

JIN Ai-juan, DING Zhe-qi, LI Shao-long, ZHANG Hao, JIANG Xiao-en

(University of Shanghai for Science and Technology, Shanghai 200093, China)

The work aims to solve the problems of slow packaging speed and worrying packaging quality of traditional packaging machinery, so as to meet the requirements of high efficiency and high precision of packaging machinery, and improve the automation level of food packaging and the economic benefits of packaging enterprises.For the permanent magnet synchronous motor with great potential, the controller and control method were studied and improved, and finally the active disturbance rejection controller was selected. The non-smooth function fal in the active disturbance rejection controller was improved to obtain a continuous and smooth tal function to reduce the flutter around the origin, and the nonlinear state error feedback rate and extended state observer were redesigned based on the tal function to achieve better control effect of permanent magnet synchronous motor. From the simulation results, tal function had better smoothness and continuity than fal function. The permanent magnet synchronous motor based on improved ADRC had better dynamic performance, steady-state accuracy, anti-interference ability and tracking ability. The optimized permanent magnet synchronous motor servo control system is suitable for occasions with high precision and frequent load changes and can effectively improve the level of packaging automation and meet the requirements of packaging industry such as high efficiency and high precision.

packaging machinery; permanent magnet synchronous machines (PMSM); active disturbance rejection control;nonlinear function

TM341

A

1001-3563(2023)01-0151-11

10.19554/j.cnki.1001-3563.2023.01.017

2022−04−17

国家自然科学基金（11502145）

金爱娟（1972—），女，博士，副教授，硕导，主要研究方向为控制理论、电机及其控制、电力电子。

责任编辑：曾钰婵