下穿隧道上盖建筑基础-地基-建筑振动传播规律分析

张学智,郭志明,傅林峰

(1.北京理工大学 后勤基建处,北京 100081;2.浙江浙工大检测技术有限公司,浙江 杭州 310014)

由于城市建筑的可用场地有限,地铁上盖建筑得到了快速的发展。地铁上盖建筑的发展可以综合利用城市土地资源,为居民上下班提供便利。然而频繁运行的地铁会产生过度的噪声和振动,并通过建筑物的承力结构传播到地铁上方的建筑物中,对居民的健康和生活质量造成不利的影响。为了分析地铁上盖建筑基础及地基振动传播规律,越来越多的学者对其进行了有限元模拟和实测分析。谢伟平等[1]通过2.5维有限元法研究地铁列车移动荷载作用引起的地基振动;刘建达等[2]通过ABAQUS有限元软件建立的隧道-地基动力相互作用分析模型对南京地铁列车运行引起的地表振动特性进行分析;黄强等[3]通过在上海地铁九号线的隧道内部、土层和地表布置传感器来统计分析轨道-隧道-地层整个空间内地铁振动传播规律;楼梦麟等[4]通过对地铁区间的地面振动进行实测,分析地铁振动在地表的衰减规律;闫维明等[5]通过分析现场实测数据,从Z振级分析地铁交通引起的地表环境振动传播规律和特性;袁葵[6]采用现场实测的方法对不同车速下地铁车辆段上盖建筑中的振动特性与传播规律进行分析;祝志文等[7]对某地铁上盖建筑的地下室结构进行振动实测,分析了地下室不同位置的振动能量分布,并对人居舒适度进行了评价;宗刚等[8]通过实测数据,对比研究了地铁邻近沿线建筑物地下室对场地振动的影响规律;许德峰等[9]以实测数据作为荷载输入,利用ETABS建立数值模型,分析建筑结构的振动响应规律;韩俊艳等[10]通过ABAQUS有限元软件建立模型,在实测数据验证模型有效性的基础上,研究地面的地铁振动响应和衰减规律;黄江华等[11]通过Dload程序模拟地铁列车运行,用数值建模的方法分析塔式楼与板式楼的振动加速度级;Sanayei等[12]通过建立波传导的一维阻抗数学模型预测结构的振动响应;Hussein等[13]通过管中管的数学模型预测建筑对列车振动的响应。地铁振动通过隧道传递至土层和建筑物中,虽然通过数值建模软件可以模拟建筑受地铁振动的影响,但由于数值模型复杂,具有不确定性的复杂系统不能很好地反映场地的振动响应水平。

为了更好地评估地铁下穿建筑物对居民健康带来的风险,笔者选取建筑地下室和地下室上部地表进行振动实测分析,并判断地铁振动响应是否超过国家相关标准。在此基础上,通过地表实测数据反演数值模型的正确性,并利用经验证后的数值模型预测建筑结构振动响应。

1 振动实测简介

1.1 项目概况

以某城市地下轨道交通线路为研究对象,该地块右侧为地铁车站,该区间隧道为明挖法方形隧道。地铁上盖建筑由6幢塔楼组成,主体结构为地下两层混凝土框架-剪力墙结构,项目平面图和地下室剖面图如图1,2所示。由于部分楼幢位于地铁通道顶板的上方,属于地铁上盖建筑,为配合地铁施工,底部整体两层地下室已竣工,选取地铁线上方楼层地下室进行地铁振动响应实测分析。

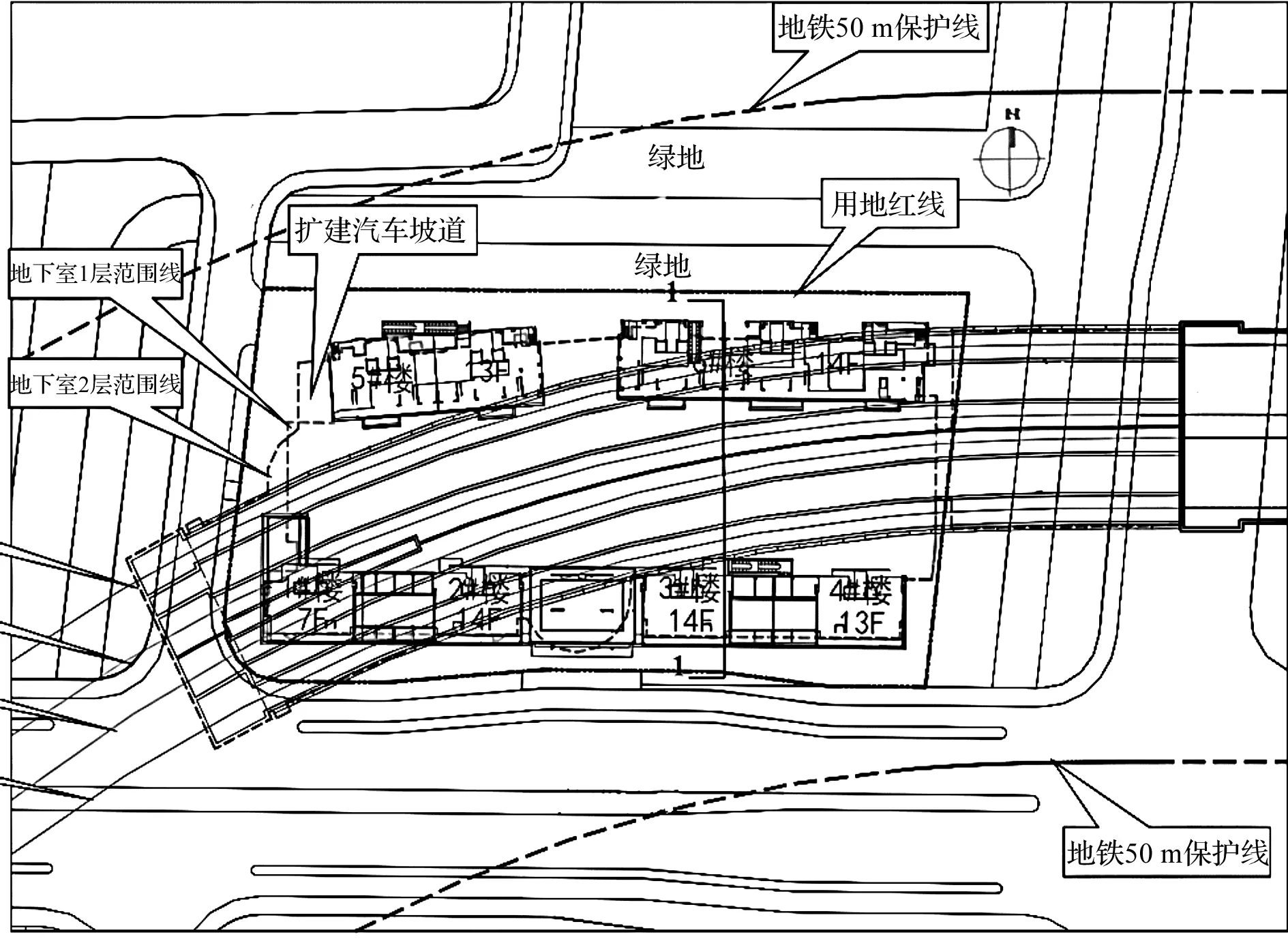
图1 项目平面图Fig.1 Plan of project

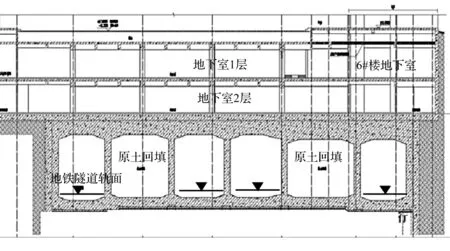
图2 地下室1-1剖面图Fig.2 Profile 1-1 of the basement

1.2 地下室和地面测点布置情况

使用INV3062C信号采集仪和941B型超低频测振仪进行现场实测分析。为了保证现场数据的有效性,采集仪连续采样时间不少于30 min。

对地下室典型楼柱和板进行现场实测,其中柱1位于地铁线下行线明挖方形隧道正上方；柱2位于明挖方形隧道侧壁正上方；板1,2分别位于柱1,2边上。测点分布如图3所示。

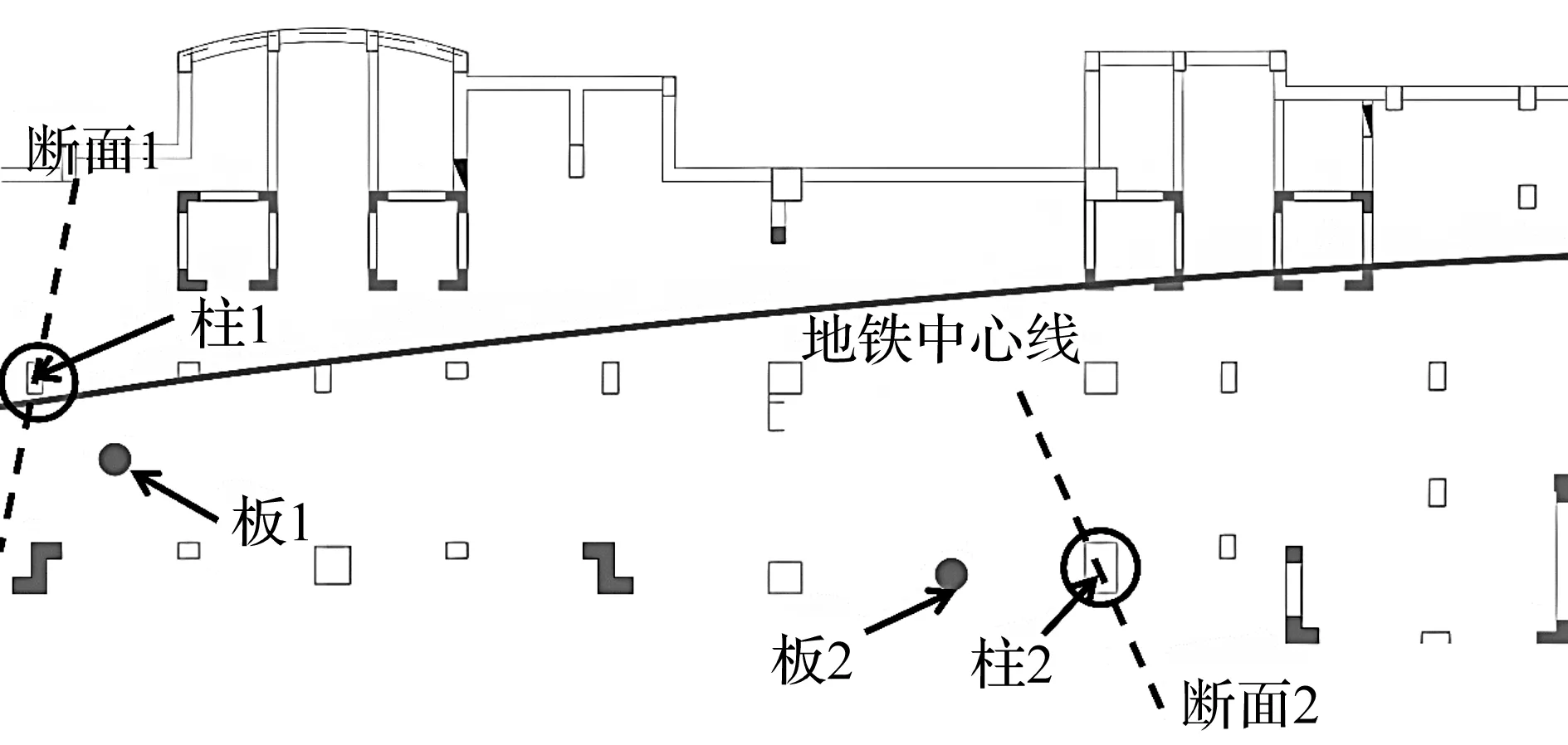
图3 地下室1，2层测点分布图Fig.3 Distribution map of measuring points in basement level 1, 2

地面测点位于4#楼边上,为了测试地面的地铁振动情况,选取测点1,2,3,4,5作为测试点,其中测点1,2,3位于地下室上方；测点4,5位于土层上方。测点平面图和剖面图如图4,5所示。

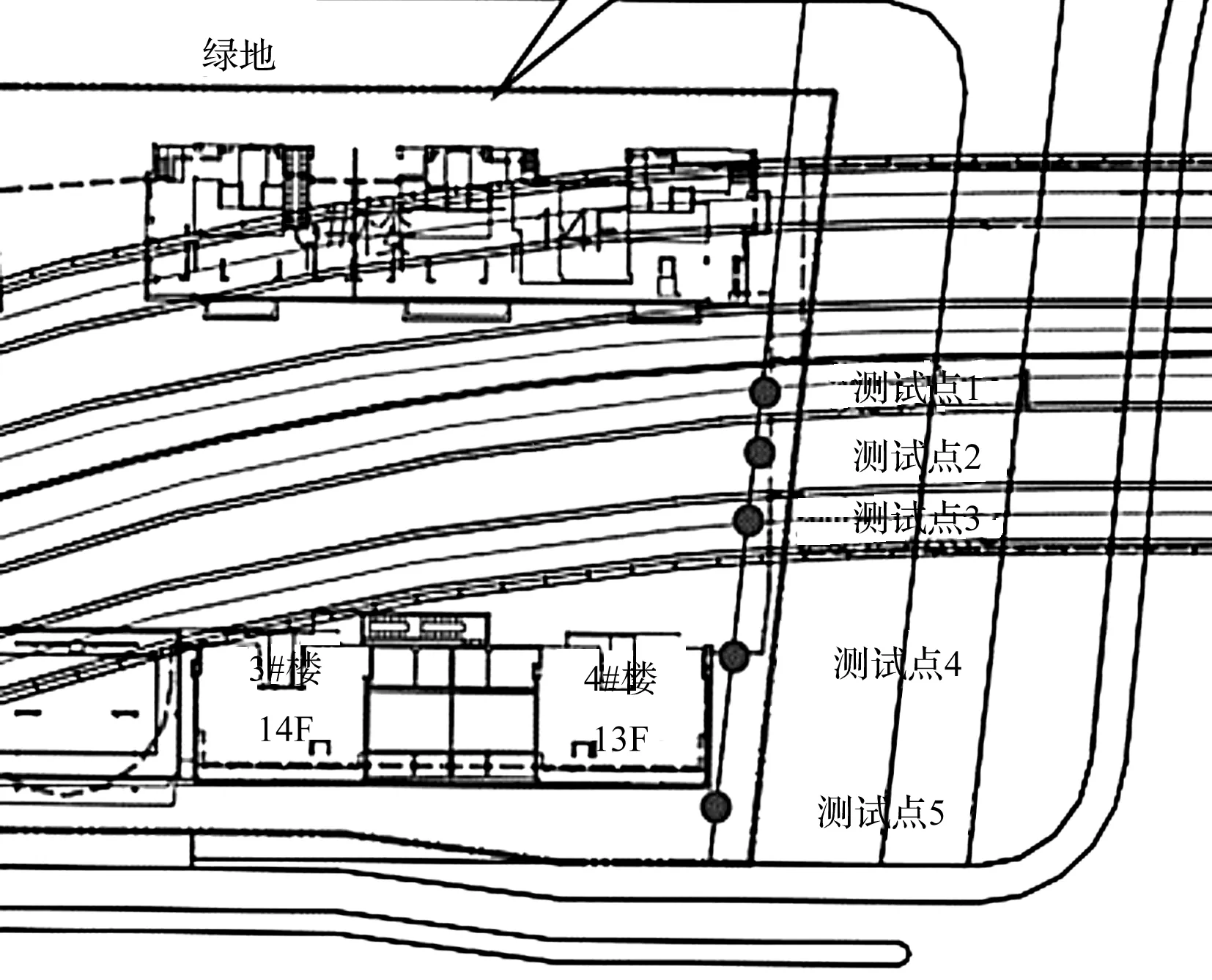
图4 地面测点平面图Fig.4 Plan of ground point

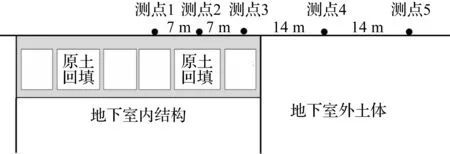
图5 地面测点剖面图Fig.5 Profile of ground point

1.3 评价标准

依据《城市区域环境振动标准》(GB 10070—1988)对地下室和地面振动响应进行评价,主要包括振动限值评价,用于验证拟建场地振动量是否符合标准，环境振动限值如表1所示。

表1 环境振动限值 单位：dBTable 1 Ambient vibration limits

该地块规划为住宅小区,执行“居民、文教区”昼间70 dB,夜间67 dB的限值标准。Z振级基于国家标准《城市区域环境振动标准》(GB 10070—1988),该标准规定了全身振动Z计权因子修正后得到的振动加速度级,总Z振级计算式为

(1)

(2)

式中:a′rms表示修正的振动加速度有效值,m/s2;a0表示基准振动加速度,一般取a0=10-6m/s2;afrms表示中心频率为f的振动加速度有效值;cf表示Z计权因子。

2 实测结果分析

2.1 地下室实测分析

地下室现场采样频率为512 Hz,采集仪采集多组过车地下室振动加速度信号,选取过车10次的算术平均值进行分析,结果如表2所示。

表2 测点统计表Table 2 Statistical table of measuring points

地下室2层地铁振动响应时程图如图6所示。由图6可知：地铁线下行线明挖方形隧道正上方柱1的振动加速度峰值为6.328 mm/s2,明挖方形隧道侧壁正上方柱2的振动加速度峰值为17.402 mm/s2,柱2的振动响应比柱1大175%,这是由于地铁隧道的振动是由隧道壁向上传递而来的,并水平传递至其他区域。同时柱2身边的板2比板1的振动加速度峰值大210%。地下室2层所测试的板振动加速度均小于柱振动加速度,这是由于地下室2层的板与隧道结构相连,刚度较大。

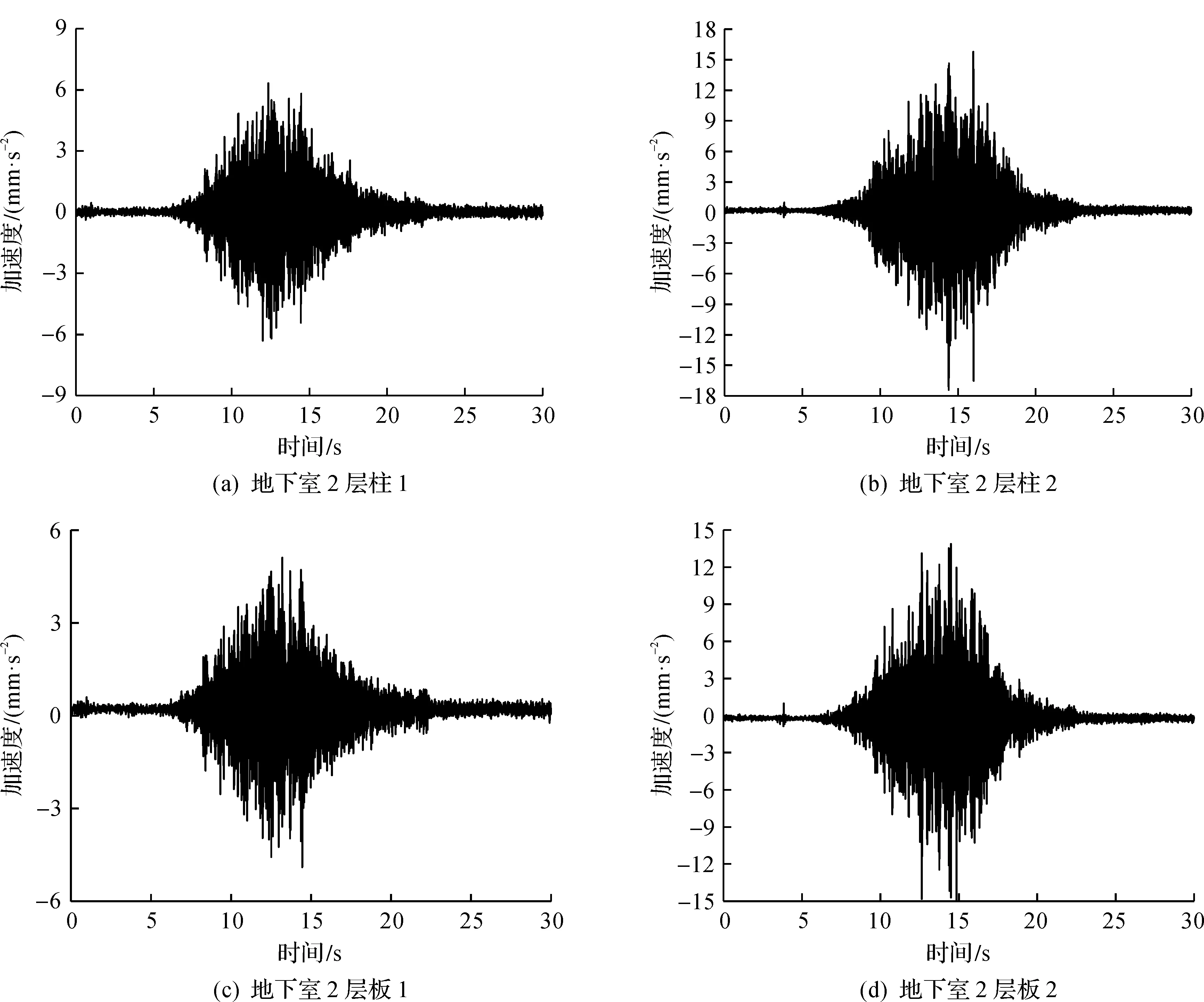
图6 地下室2层振动响应时程图Fig.6 Time domain diagram of vibration response of basement level 2

地下室1层的地铁振动响应时程图如图7所示。由图7可知：地下室1层柱1的加速度峰值为5.969 mm/s2,柱2的振动加速度峰值为10.07 mm/s2,柱2的振动响应比柱1大68%,由柱1与柱2的振动响应水平可知,柱上的振动向上衰减,且柱2的衰减大于柱1,这可能是由于柱2的截面大于柱1的截面。地下室1层的板振动加速度大于柱振动加速度,这可能是由于地下室1层板的振动由多个竖直方向地下室2层柱向上传递并叠加导致的,并且地下室1层板的刚度远远小于地下室2层与隧道相连的板。

图7 地下室1层振动响应时程图Fig.7 Time domain diagram of vibration response of basement level 1

对所测试的点位进行Z振级评价,评价结果如表3所示,Z振级均满足《城市区域环境振动标准(GB 10070—1988)》规定的居民、文教区昼间限值要求。

表3 地下室振动响应评价表Table 3 Evaluation table of basement vibration response

2.2 地表实测分析

地表测点实测时程图如图8所示。由图8可知：测点1～3位于地下室上方,地铁振动主要通过地下室柱向上传递,且处于地下室顶板,振动在此处叠加,导致地面振动较大,然而传递规律不明显。其中,测点2在原土回填上方,振动响应较小;测点4,5位于土层上方,地铁振动主要由土层向上传递,由于土层的滤波作用,测点4,5的振动较小。地铁过车引起地面测点3～5的振动沿地铁横向呈波动衰减趋势,当距地铁正上方横向间距大于7 m时,地面测点的Z振级满足夜间规范要求,结果如图9所示。

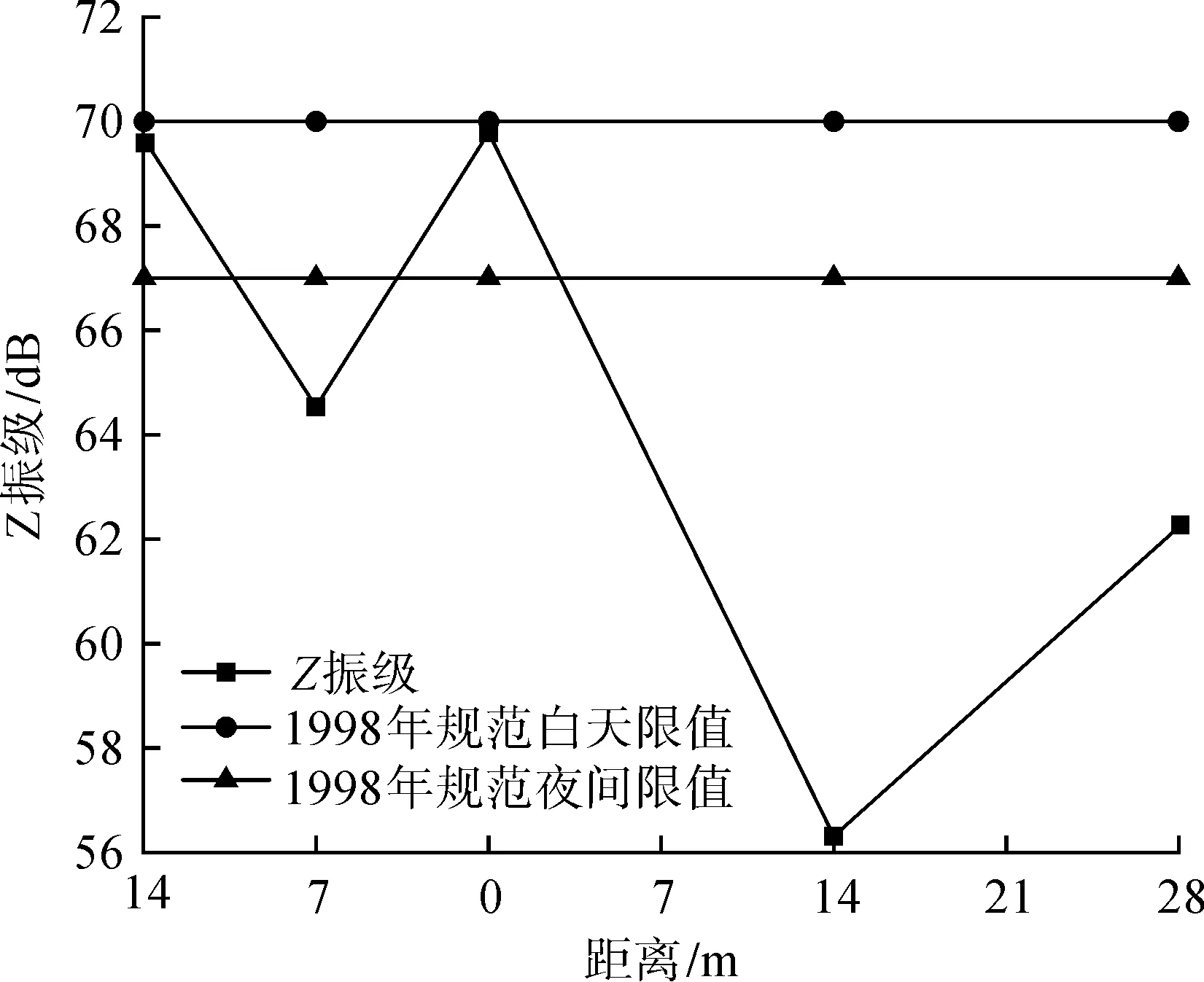
图9 地表测点振动响应折线图Fig.9 Broken-line graph of vibration response at surface points

3 数值模拟分析

使用有限元软件ABAQUS建立移动荷载-隧道结构-周围土体-上盖建筑有限元模型,结合Fortran程序编制移动荷载子程序VDLOAD,通过VDLOAD建立荷载空间位置和时间变化的关系,有效地实现幅值改变的荷载移动特性。列车运行引起周围土体及上盖建筑的动力响应计算模型如图10所示。在建立数值模型时使用三维模型进行计算分析,有限元区域范围为100 m×100 m×70 m,四周及底面为5 m厚的无限元边界,用于逸散边界的波动能量。列车为AH车型,6辆编组,车长为19 m,轴距为2.3 m,车辆定距为12.6 m,轮对作用力通过VDLOAD施加在轨道结构上,轨道采用60.64 kg/m钢轨,轨距为1.435 m,隧道管片厚为0.350 m,内径为5.500 m,混凝土等级为C50。

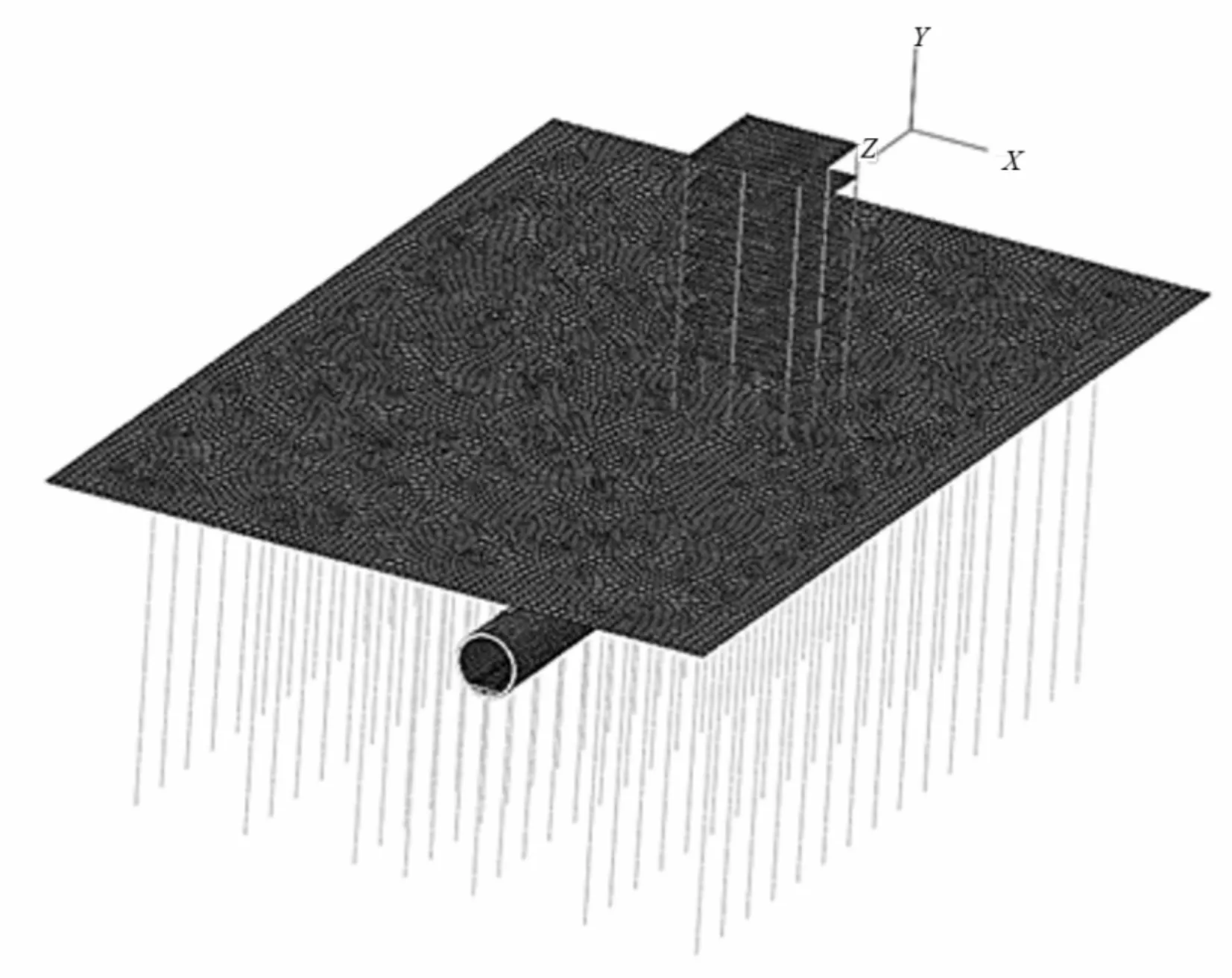
图10 轨道-隧道-地基-结构模型示意图Fig.10 Schematic diagram of track-tunnel- foundation-structure model

建立隧道结构-周围土体模型,选取隧道正上方地表测点进行振动实测与模拟的对比验证,该方法将列车荷载简化为由一系列不同幅值正弦力组合而成的力荷载,通过调整不同频率的正弦力的幅值,构建不同频率分布特征和强度的人工列车荷载,即

(3)

式中:F(t)表示列车单个车轮t时刻平均作用力;ω表示单个车轮平均承担的列车重量,N;θi表示相位差;φi表示频率i正弦力幅值调整系数;n表示关心振动频率的个数;t表示荷载作用时间。

该数值模型重点关注地铁过车引起上盖建筑的振动响应,地铁轨道及其近场位置振源特性不是研究重点,因此模型采用基于场地土实测振动数据反演求解列车荷载的研究方法,分析隧道上盖建筑振动传递特性,保证所关心上盖建筑振动的计算精度,反演具体思路:在轮-轨接触界面输入由一系列不同幅值正弦力组合而成的力荷载,通过调整不同频率正弦力的幅值,构建不同频率分布特征和强度的人工列车荷载,结果如图11所示。

图11 实测与数值模拟对比Fig.11 Comparison between measurement value and numerical simulation

通过地表振动实测信号的数值反演,可使地基测点各个频率的模拟值与实测值相吻合,该方法适用于已建地铁隧道线路,用于邻近建筑振动预测。地铁线邻近建筑典型楼栋的振动预测值如图12所示。由图12可知：Z振级随着楼层的升高呈现出先减小后增大的趋势,从地下室至2层振动响应单调衰减,随着楼层高度的进一步增加,振动响应又呈现出增大的趋势,在顶楼振动响应达到峰值,其原因是顶部楼层存在波动反射。

图12 振动响应沿楼层衰减示意图Fig.12 Diagram of vibration response along the floor

4 结 论

对与地铁明挖隧道相连的上盖建筑地下室和地表进行了实测分析,通过经地表实测数据验证的数值模型预测上盖建筑的振动响应,得到以下结论:1) 地铁振动主要通过隧道壁和地下室结构柱向上传递,地下室1层柱的振动加速度峰值比地下室2层柱小,但由于地下室2层板受到地下室2层柱的叠加作用,导致地下室1层板振动响应大于地下室2层;2) 地铁过车引起的地基振动响应沿地铁横向呈波动衰减趋势,当距地铁正上方横向间距大于7 m时,地面测点的Z振级满足规范要求;3) 所提数值模型适用于已建地铁隧道线路,可用于邻近建筑振动预测,数值模拟值与地表实测数据比较符合;4) 由模型模拟结果可知,各楼层Z振级满足规范要求,地铁振动响应随层数的增大呈现出先减小后增大的规律。