EMD-IVMD方法在验潮站水位序列降噪中的应用

郇常敏,周世健,鲁铁定,贺小星,徐华卿

(1.东华理工大学 测绘工程学院，南昌 330013；2.南昌航空大学，南昌 330063；3.江西理工大学 土木与测绘工程学院，江西 赣州 341000)

当前海平面的急剧变化使人们对验潮站数据的研究逐步加深，验潮站水位序列受板块边界的构造运动、冰川均衡调整以及其它误差的影响变得十分复杂[1]，且其有非平稳、非线性等特点。因此，如何对验潮站中的水位序列进行有效地降噪，使其发挥积极作用，具有重要的现实意义。验潮站坐标时间序列在海平面变化、潮汐模型建立及海洋垂直基准建立等科学研究和工程建设等方面应用广泛，其作用对于气候变化、海洋自然灾害、海岸带工程的建设具有重大意义[2-4]。

在信号分析处理领域，许多专家学者进行了深入的研究，比如Huang等[5]提出了一种用于信号分析的方法—经验模态分解(empirical mode decomposition,EMD)，在处理非平稳、非线性信号数据的降噪方面应用广泛。在EMD方法的应用方面，张双成等[6-7]针对GPS时间序列具有的一系列问题，采用EMD的方法对中国区域内的IGS站时间序列的N,E,U方向进行处理，最终实现GNSS时间序列信号的有效降噪；同样鲁铁定等[8]针对采用相关系数准则确定临界分量K值不确定的问题，提出一种利用综合评价指标T的新型EMD降噪方法。最终在EMD方法的基础之上,Wu等[9]在原始信号中添加不同强度的高斯白噪声，提出整体经验模态分解的降噪方法。

在Dragomiretskiy等[10]提出一种新型自适应复杂信号分解方法—变分模态分解方法之后；Xu等[11]针对传统的VMD(variational mode decomposition)方法在降噪过程中存在无法确定分解模态函数(IMF)个数以及惩罚因子的取值的问题，提出了一种以能量熵互信息(eneergy entropy mutual information,EEMI)作为目标函数的改进变分模态分解(VMD)与小波包结合的降噪算法；鲁铁定等[12]针对变形监测数据中分解含有的噪声难以去除等问题，提出一种变分模态分解与样本熵相结合的方法；罗亦泳等[13]提出改进变分模态分解算法(improved variational mode decomposition，IVMD)构建变形特征提取新方法，这些方法模型的结合与改进使得VMD方法的性能有了比较大的提升。为了识别轴承早期故障，Zhou等[14]提出了一种基于自适应变分模态分解(VMD)的轴承早期特征提取方法,该方法不仅改善了蝗虫优化算法(grasshopper optimiztion algorithm,GOA)的局部最优问题，而且可以自适应地确定VMD的模态数和惩罚参数。徐新等[15]针对变压器故障诊断中传统的BP神经网络算法效率低、收敛速度慢等缺点，提出一种基于蝗虫优化算法的神经网络的故障判断方法。

基于以上研究，综合考虑变分模态分解的参数优化和验潮站水位序列的特性，以及经验模态分解的适用性，采用一种EMD与IVMD相结合的降噪方法，并结合实验比较本文方法与传统的EMD与EEMD(ensemble empirical mode decomposition)方法的降噪效果。

1 原理理论与方法

1.1 EMD降噪原理

经验模态分解(EMD)方法可将时间序列分解为若干分量，在处理非平稳、非线性信号方面非常有效。该方法可将原始信号分解为若干个频率由高到低的分量(本征模态函数)和一个残余项，最终将残余项与低频的IMF分量进行重构可实现信号的降噪。分量必须满足的两个条件是[5]：①在整个数据段内，极值点的个数和过零点的个数必须相等或相差最多不能超过1个。②在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为0，即上、下包络线相对于时间轴局部对称。

原始信号被分解后的表达式为:

(1)

式中：x(t)为原始时间序列；t=1,2,…,N；m为EMD分解所得本征模态函数的个数；K为本征模态函数分量的序号；r(t)为残余项;IMFk为分解后得到的本征模态函数分量。

原始信号进行EMD分解的过程为：①找出原始信号x(t)的极大值和极小值点，计算出上、下包络线的均值T1,将原始信号减去该包络均值，得到1个新的序列C1(t)；②重复进行步骤①)，直到满足IMF阈值条件为止，则可得到IMF分量；③将原始时间序列x(t)减去第1个IMF分量形成1个新的数据序列x′(t),重复步骤①和②，最终得到m个IMF分量，残余项满足单调条件才可行。

原始数据序列经EMD分解之后，需要确定临界的IMF即低频信号与高频信号的分界点，可采用相关系数准则来判断，互相关系数的首个极小值点时对应的IMF分量即为分界IMF的最佳预估项。判断公式如下：

(2)

式中:Pk为第k个IMF分量与原始序列的相关系数;IMFk(t)为分解后得到的本征模态函数分量;x(t)为原始数据序列。

针对EMD模态混叠等问题，利用高斯白噪声具有频率均匀分布的统计特性，通过每次加入同等幅值的不同白噪声来改变信号的极值点特性，然后对多次EMD得到的相应IMF进行总体平均来抵消加入的白噪声，从而有效抑制模态混叠的产生，即为集合经验模态分解 (EEMD)方法，其本质则是一种叠加高斯白噪声的多次经验模式分解[9]。

1.2 IVMD降噪原理

1.2.1 VMD算法

VMD(变分模态分解)分解是一种自适应分解方法，本征模态函数(Intrinsic mode function，IMF)被定义为一个有带宽限制的调幅-调频函数,VMD算法是通过设置模态数、惩罚参数和上升步长等参数将信号分解成K个中心频率为ωk的模态函数，其实质为变分问题的构造和求解。VMD算法构造约束变分问题可表示为[6]：

(3)

式中:x(t)为原始数据序列；μk(t)为模态函数；ωk为各模态函数的实际中心频率；e-jωkt为各解析信号的预估中心频率。为求解该约束变分问题，引入拉格朗日乘子λ(t)和二次惩罚因子α，将该约束变分问题转换为无约束变分问题，因此增广的拉格朗日表达式为：

L(μk(t),ωk,λ(t))=

(4)

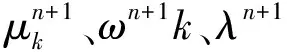
1.2.2 IVMD算法

鉴于验潮站水位序列具有非线性、非平稳的特点，且其包含的噪声复杂，用单一指标来获取信号的特征相对困难，多个单一指标的融合可提供更强的鲁棒性。因此对于VMD的参数确定问题，文中采用由能量熵和互信息组成的能量熵互信息(EEMI)指标，采用两个模态函数的能量熵互信息之和作为目标函数，利用GOA算法对VMD参数进行优化。蝗虫优化算法(GOA)是由Shahrzad Saremi等[15]提出的一种启发式仿生优化算法，其优点是搜索效率高和收敛速度快，该算法模拟的是自然界中蝗虫群体的捕食行为。该算法主要分为探索和开发两个步骤：在探索过程中蝗虫群体长距离快速跳跃，这一阶段有利于全局搜索；在开发中蝗虫群体只在小范围跳跃，有利于局部搜索。

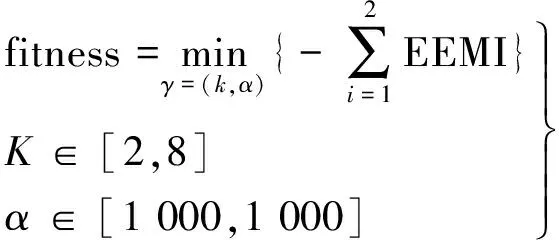
(5)

式中，fitness为目标函数；γ=(K,α)为VMD参数的取值范围；EEMI=EEMI,EE、mi分别为能量熵和互信息，其计算式为：

(6)

(7)

式中：(X;Y)～p(x,y)，其中p(x,y)是X和Y的联合概率分布函数，而p(x)和p(y)分别是X和Y的边缘概率分布函数；Ei是频域中振动信号的能量分布；IMFi(t)是不同频率带宽的模态分量。

利用样本熵(SE)能够反映信号复杂程度的特性，在该改进的VMD方法中采用样本熵作为判断噪声部分与水位序列中真实信号的标准.

2 EMD-IVMD算法

EMD是一种自适应性信号处理方法，在处理非线性、非平稳信号方面有其独特的优势，且VMD同样是一种新型信号处理方法，针对传统VMD无法确定固有本征模态函数的个数和惩罚因子的数值，采用蝗虫优化算法(GOA)优化目标函数的一种新型改进的VMD方法，并将EMD与改进的VMD进行结合，分别处理不同频率阶段的信号，以展示出其优势。

经验模态分解(EMD)与基于蝗虫优化算法优化目标函数的变分模态分解(VMD)在验潮站水位序列的降噪步骤如下:

1)对原始序列进行EMD分解，得到一定数量的本征模态函数(IMF)。

2)采用相关系数准则确定低频分量与高频分量的分界点，即相关系数首次出现局部极小值则认为是信噪分界点的最佳预估项。

3)分别将低频分量与高频分量进行重构。

4)设置VMD算法参数的范围，初始化GOA算法参数；在文献[16]中模态数K∈[2,8],并且惩罚因子α∈[1 000,10 000]，通过文献[17]可得K和α的取值范围应为[2,8]和[1 000,10 000],GOA算法的种群数N=30,最大循环数L=10。利用最优参数的VMD将重构后的高频IMF分量进行再次分解，计算各IMF分量的样本熵，设定SE的阈值，将大于该阈值的视为噪声部分，小于该阈值的分量视为信号将其进行重构。

5)最后将EMD重构的低频信号与IVMD处理后的重构信号叠加作为最终滤波后信号。EMD-IVMD的具体实施步骤见图1。

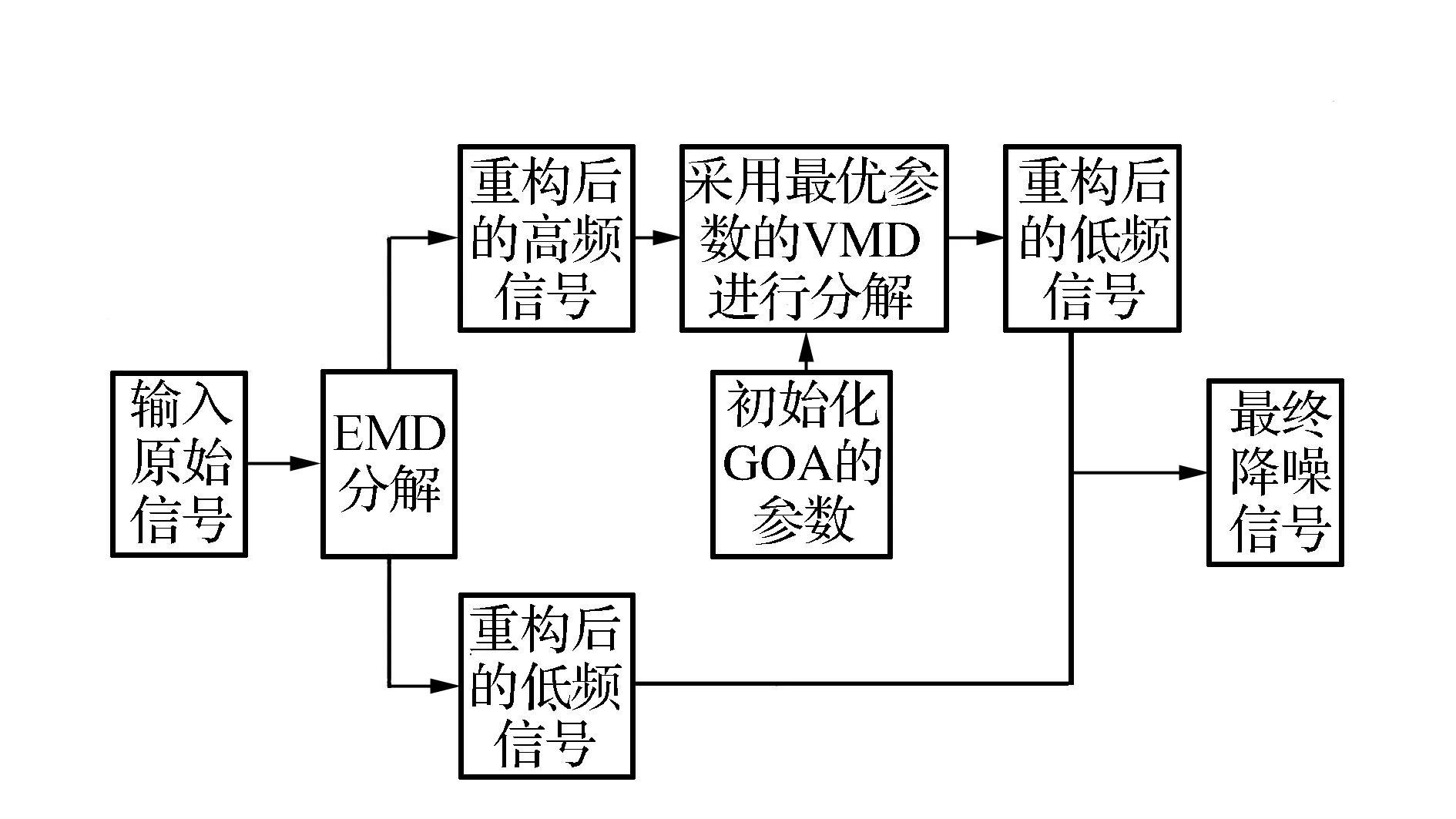
图1 EMD-IVMD组合方法流程

选取信噪比(SNR)与均方根误差(RMSE)来评价该组合方法的降噪效果，算式为：

(8)

式中：x(t)为原始时间序列；s(t)为降噪后信号；N为时序信号长度。

(9)

式中:s(t)为经EMD-IVMD分解后重构的信号，特别说明仿真实验部分式(15)中的x(t)为未加噪的真实信号，实测数据实验部分x(t)则表示含噪数据序列。对于仿真实验，信噪比越高，RMSE越小，表明滤噪效果越好，提取的信号越接近于真实信号；对于实测数据中，若信噪比越高，RMSE越小，表明滤噪效果越好且提取的有用信号更多。

3 实验数据分析

3.1 模拟数据实验

模拟数据主要有3个恒定振幅的周期项和高斯白噪声来组成，其设置采样频率为1 HZ，采样点数为1 024个，加入信噪比为6 dB的白噪声(Noise)，该模拟信号构成分量波形如图2所示。表1为模拟信号在不同方法下的精度指标对比，模拟数据表达式为：

(10)

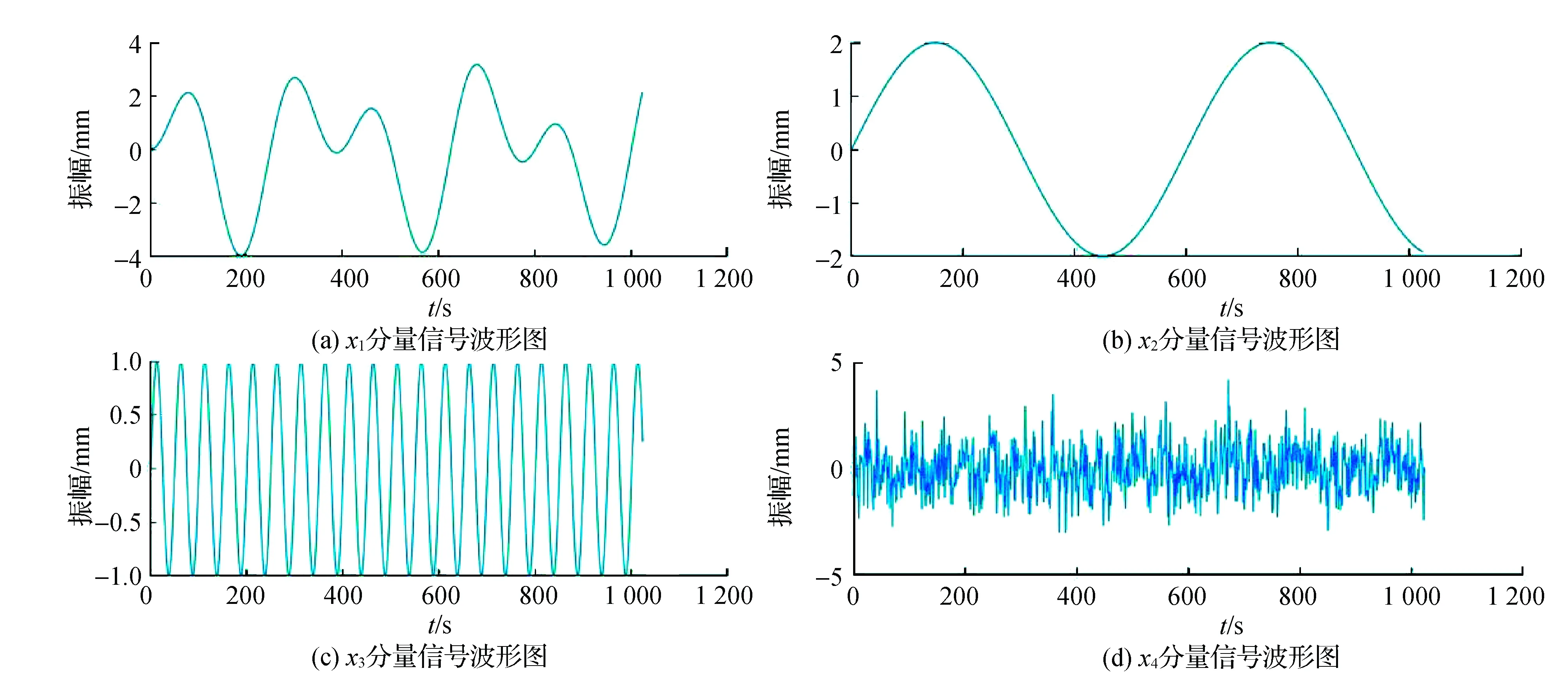
图2 构成模拟信号的分量信号波形

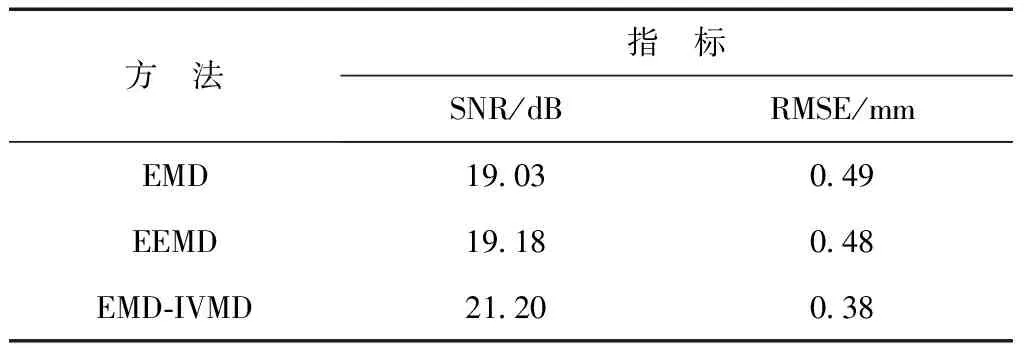
表1 模拟信号在不同方法下的精度指标对比

图3为模拟数据的加噪信号波形，图4为模拟信号与采用3种方法降噪后的信号波形对比图。从图4可以看出由EMD-IVMD方法处理后的重构信号与加噪模拟信号相比其波形非常相近且其信号曲线的光滑程度要更高，而通过传统的EMD和EEMD方法处理后的信号波形与加噪模拟信号的波形存在一定的差异且其信号曲线的光滑程度过高，分析其原因可能是过分滤除真实信号，使其丢失部分真实信号。由上述分析得出，EMD-IVMD方法比传统的EMD和EEMD方法降噪效果更明显，提取有效信号的效果更优。

模拟数据实验中，在IVMD进行分解时，GOA算法优化后的K=3,α=1 051。为了定量说明这3种方法的去噪效果，采用信噪比(SNR)和均方根误差(RMSE)两个指标，表1为模拟数据经3种方法去噪后的两种降噪效果评价指标值。由表1可知，在模拟数据中，EMD-IVMD方法与EMD、EEMD方法相比，EMD-IVMD方法重构后的信号的SNR相对分别提高了11.40%和10.53%，且RMSE相对分别减小了22.45%和20.83%。综上所述，模拟实验结果表明EMD-IVMD方法相比于EMD和EEMD方法去噪效果更优。

图3 模拟数据的加噪信号波形

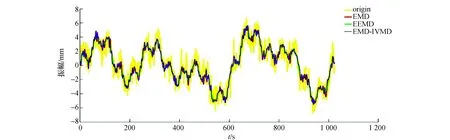
图4 模拟信号与各方法重构信号对比

3.2 实测站水位序列实验分析

为验证本方法对实际验潮站水位变化序列的降噪效果，采用OLANDS NORRA UDDE(69站),CUXHAVEN 2(7站),AARHUS(76站),ESBJERG(80站)4个验潮站的实测数据进行分析，数据来源于PSMSL网站，(http://www.psmsl.org/data/obtaining/stations/52.php)。OLANDS NORRA UDDE站所选数据为1887—2020年跨度为133年的时间序列，CUXHAVEN 两站所选数据为1843—2018年跨度为175年的时间序列数据，AARHUS站所选数据为1888—2017年跨度为129年的时间序列数据，ESBJERG站所选数据为1889—2017年跨度为128年的时间序列数据。在进行实验之前，去除序列中较大的粗差，将剔除粗差的时间序列作为本实验的原始时间序列，经观察分析剔除粗差后的信号振幅明显要小于未剔除前，说明达到了较好的剔除粗差的效果。限于篇幅有限，仅以76站(AARHUS)为例进行展示分析，图5为76站原始序列信号与经3种方法降噪后的重构信号对比图，特别说明图5中展示的为水位变化序列(扣除序列平均值)。通过图5观察分析可知，EMD，EEMD方法对水位序列处理后其形成的水位序列曲线虽平滑，但其过量滤去了其中的真实有用信号，其振幅波动范围与原始信号有着较大的差异。而EMD-IVMD方法所形成的序列曲线，在滤去部分噪声后，其信号振幅波动范围与原始信号有着相近的趋势且一致性较好。

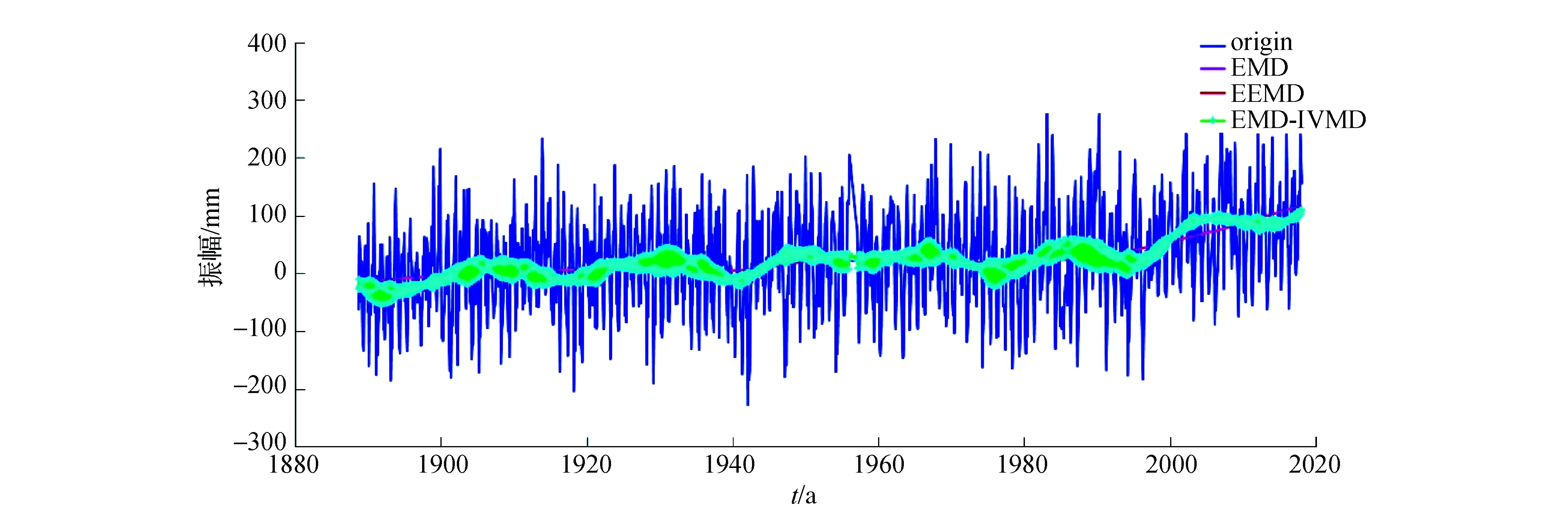
图5 76站重构信号与原始信号对比

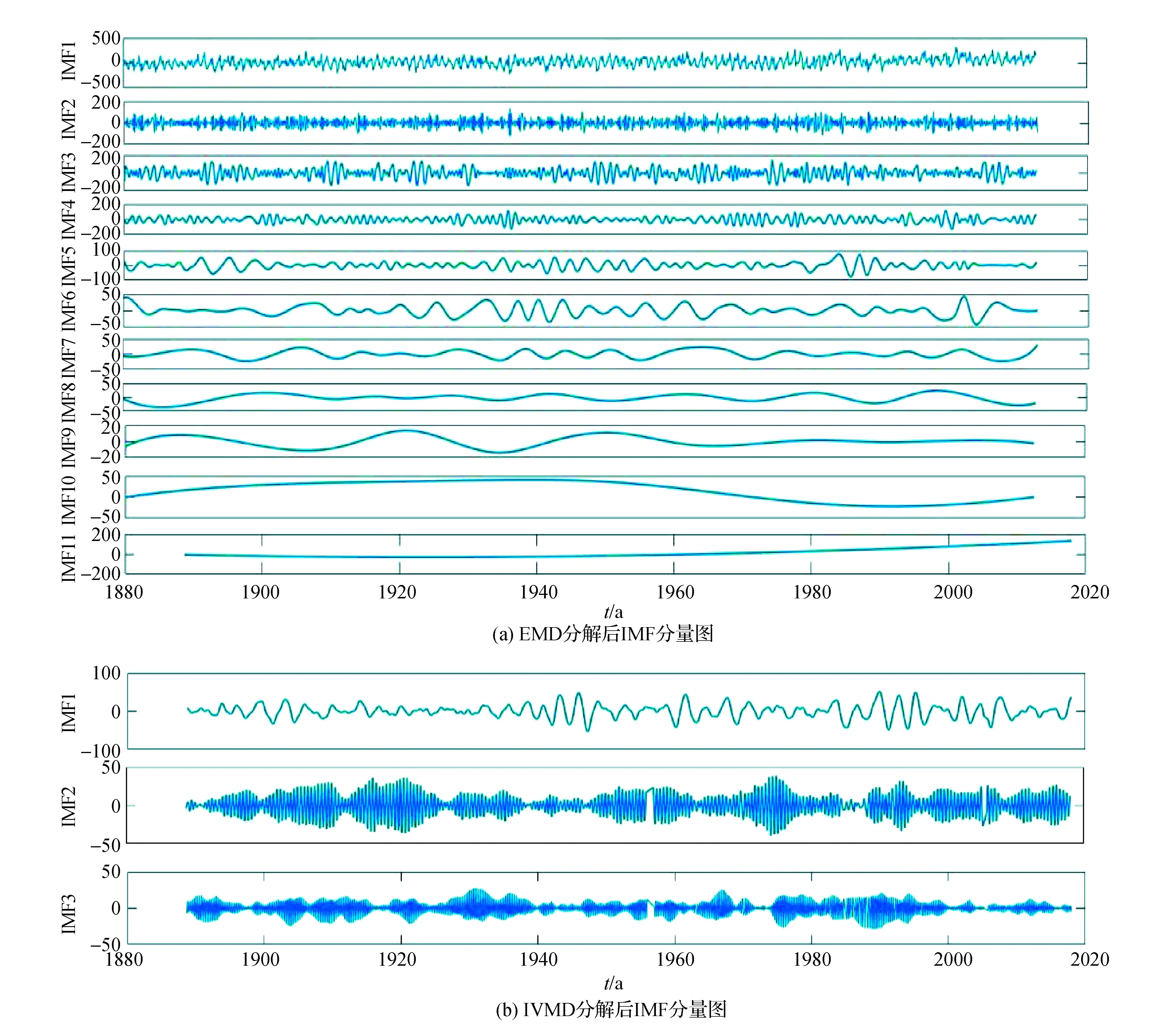
图6 76站经EMD-IVMD分解后IMF分量图

如图6所示为76站经EMD-IVMD方法处理后的IMF分量图，且第一次经EMD分解后产生了11个分量，通过相关系数法确定临界的IMF分量为第6个，将前6个IMF分量进行重构，而且通过观察分析图6，前6个IMF表现出明显的随机特性，所以再结合相关系数法可以推断出前6个IMF为噪声部分。第二次IVMD对重构后的时间序列进行分解，且分解后产生3个IMF分量。图6(a)为76站原始时间序列经EMD分解后的IMF分量图，图6(b)为经IVMD分解后的IMF分量图。因为EMD-IVMD方法要进行两次分解，在对第76站进行第二次分解时GOA算法优化后的K=3,α=9 688，在第二次分解后，计算各模态分量的样本熵，如表2所示为IVMD分解后各模态分量样本熵，且分解后得到的3个模态分量的样本熵分别为0.69、0.70和0.74，所以通过大量实验分析最终确定阈值为0.71，将IMF1、IMF2重构后与经过第一次分解后的重构信号再次重构得到最终降噪信号。

表2 IVMD分解后各模态分量样本熵

表3给出了4个实测验潮站经3种方法处理后的精度评价指标，通过表3和图5可以看出对于4个验潮站，EMD-IVMD与EMD和EEMD两种方法相比，均方根误差较小且信噪比较大，表明EMD-IVMD方法能够更好地滤除噪声并提取更多的有用信号。此外发现EMD与EEMD相比，EMD评价指标略优于EEMD，两者较为接近，可能源于验潮站数据序列中噪声以有色噪声为主，需进一步分析。76站(AARHUS)水位变化序列通过文中提出的方法处理后，SNR降噪指标相比于其余两种方法提高了0.46%和0.62%，EMD-IVMD滤噪效果较好，RMSE相对分别减少了8.16%和14.41%。

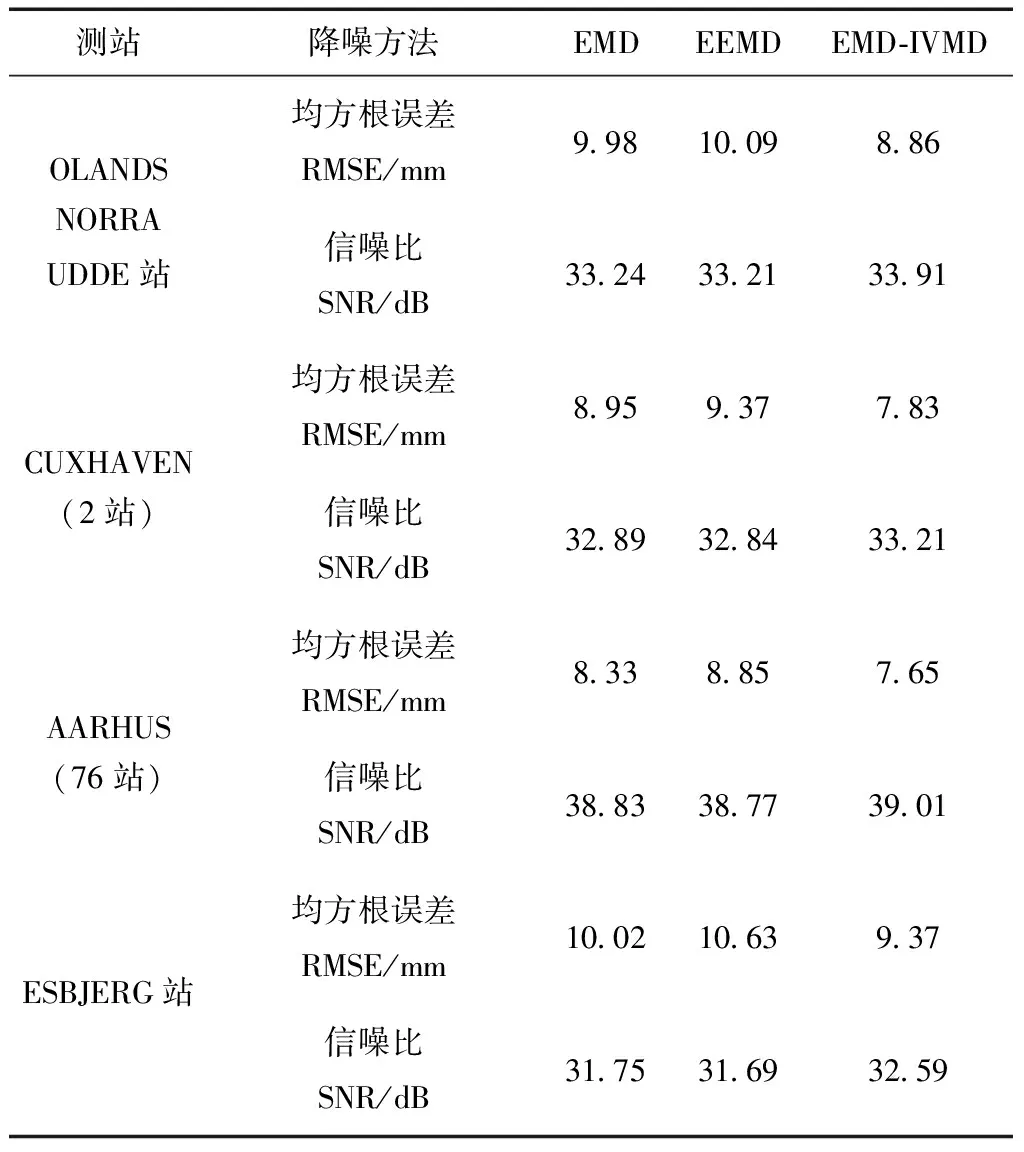
表3 4个实测站降噪指标值对比

4 结 论

针对验潮站水位变化序列的非线性非平稳特性，提出一种融合EMD与蝗虫优化算法的VMD方法的滤波算法。该方法需要对数据序列进行两次分解，首次利用EMD分解提取出高频含噪部分和低频信号部分，并重构得到以高频噪声为主的分量以及以信号为主的低频分量。对重构的高频噪声分量进行IVMD分解，将其含有的部分有效信号提取出来。最后将EMD首次提取的低频重构分量与IVMD提取的有效信号叠加得到滤波后最终信号。文中通过模拟实验以及实测验潮站水位序列数据进行分析，并评估EMD、EEMD和EMD-IVMD 3种方法的滤波效果。仿真结果显示，文中提出的EMD-IVMD方法更能有效地提取出高频噪声部分，降噪效果要明显优于传统的EMD和EEMD方法。实测数据结果表明，与传统的EMD和EEMD方法相比，4个验潮站EMD-IVMD方法的信噪比平均分别提高了1.67%和1.52%，均方根误差平均分别减小了9.59%和13.51%。