选区激光熔化316L不锈钢残余应力优化研究
2023-02-01王翠凤刘思默廖小玲佟一璇
王 涛,王翠凤,刘思默,廖小玲,佟一璇
(福建信息职业技术学院,福州 350000)
人工神经网络是用简单的数学模型来对生物神经网络结构进行描述,近年来,因具有独特的结构和信息处理方法,使其在许多应用领域中得到广泛应用。增材制造技术是一种将粉末或丝材快速熔化,采用逐层堆积的方式制造复杂几何形状部件的一种快速成形工艺,选区激光熔化技术能够成形复杂结构的金属零部件,在工业应用中具有其独特优势[1]。在成形过程中,由于金属材料熔池的快速熔化和快速凝固会出现较大的温度梯度,形成不均匀的温度场,导致在零部件内部极易存在较大的残余应力[2]。过大的残余应力会影响零部件的机械强度和使用寿命,严重时会在零部件的内部产生缺陷或者裂纹。张会莹[3]研究选区激光熔化成形IN738LC合金过程中应力场的分布规律,廖英岚[4]对选区激光熔化成形GH4169高温合金过程中的残余应力演变进行研究,文舒等[5]对GH536高温合金选区激光熔化过程中熔池区域的温度场及凝固后的残余应力分布进行研究。
本文采用遗传算法对BP神经网络的初始连接权值和阈值进行优化,建立以激光功率、扫描速度、扫描间距和铺粉厚度作为输入参数变量,以选区激光熔化成形316L不锈钢残余应力作为输出目标变量的预测模型,为选区激光熔化成形316L不锈钢的工艺参数优化奠定理论基础。
1 试验方案
1.1 设备与材料
试验设备使用德国SLM Solution公司研发生产的SLM 125设备。其主要由激光器、光路传输系统、气体保护系统、密封成形室和机械控制系统等组成。激光器采用IPG公司生产的连续光纤激光器,光路传输系统由光束隔离器、光束扩展器、扫描振镜和f-θ透镜等组成。试验采用的粉末为316L不锈钢粉末,粉末颗粒形状为球面形,其在扫描电镜下观察的微形貌如图1所示。

图1 316L不锈钢粉末形貌
1.2 试验方法
响应面法是利用统计学原理解决复杂试验变量与试验指标之间关系的一种方法,建立设计变量与响应变量之间的全局函数,中心组合试验设计是响应面法研究中最常用的二阶设计方法。本文选取激光功率、扫描速度、扫描间距和铺粉厚度作为自变量,将选区激光熔化成形316L不锈钢残余应力作为响应变量,采用4因素5水平的CCD设计模型用于设计试验,其工艺参数与水平见表1。

表1 工艺参数与水平
试验前将316L不锈钢粉末置于真空干燥箱中进行时长为5 h,80℃的真空烘干,成形尺寸为10 mm×10 mm×10 mm的立方体方块。使用便携式PROTO残余应力测试仪进行选区激光熔化316L不锈钢残余应力的测试,选用Cu靶,hkl平面为211,对称型面为BCC,Bragg角为163.48,泊松比选用0.28,弹性模量为213.64 GPa,检测结果如图2所示。
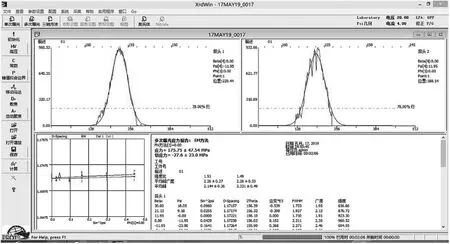
图2 残余应力检测结果
2 结果与讨论
2.1 数据分析与处理
残差是指试验实际值与模型预测值之间的差值,通过残差分析可以判断试验数据的可靠性及响应面模型是否符合方差分析的假设条件。图3为残差正态概率分布示意图,从图中可以看出30组数据响应值呈线性分布,说明标准偏差偏离实际值与预测值的程度小。图4为预测值与实际值对应关系图,从图中可以看出数据呈良好的线性分布,没有出现异常的数据点。
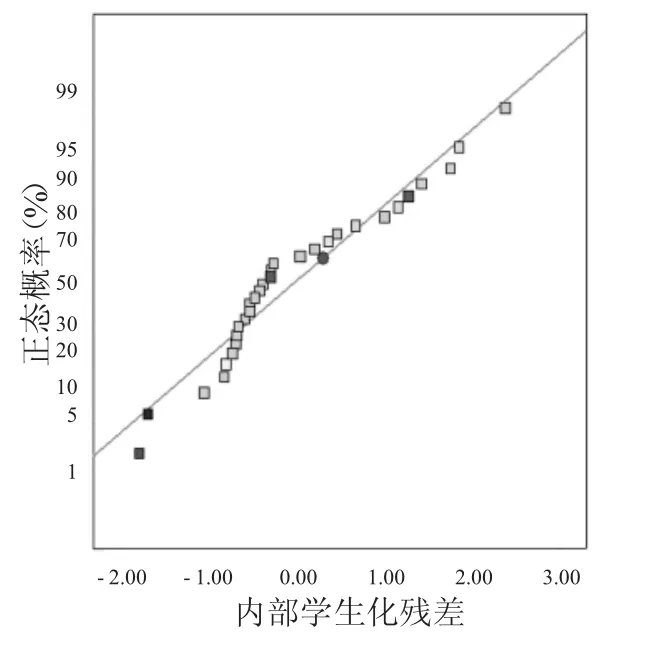
图3 残差正态概率分布示意图
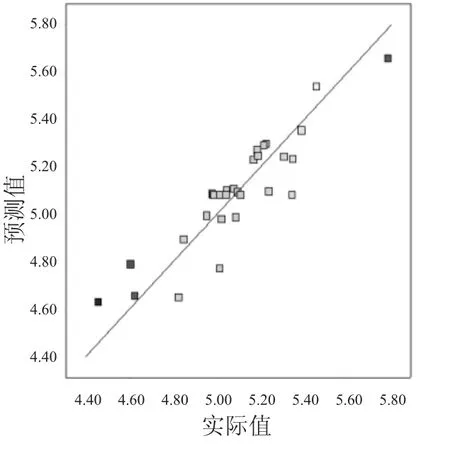
图4 预测值与实际值对应关系图
神经网络的输入和输出数据因其量纲不相同,会导致神经网络收敛慢、训练时间长等问题。因此,在训练神经网络模型前一般需要对训练样本进行归一化处理,避免因数据差别大而造成的网络预测误差,选用归一化函数为mapminmax函数,将统计后的训练样本数据进行归一化处理至[-1,1]区间。
2.2 神经网络模型建立
BP神经网络采用误差反向传播算法,是目前应用最为广泛的神经网络。本文选取激光功率、扫描速度、扫描间距和铺粉厚度作为网络的输入参数,选取成形残余应力作为网络的输出参数。在网络结构选取方面,根据Kolmogorov定理可知,在满足合理的权值系数选取时,3层前馈网络可以逼近任意连续函数,因此采用具有单隐含层的3层网络结构,建立选区激光熔化成形316L不锈钢,BP神经网络模型如图5所示。
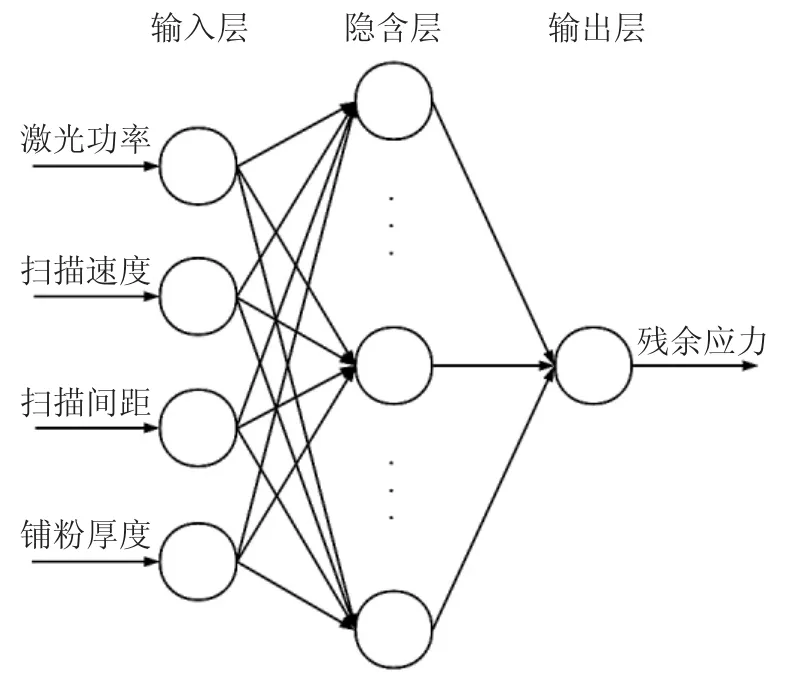
图5 BP神经网络模型
中间隐含层的节点数目对网络的学习能力、速度、精度有很大的影响,是BP网络结构是否可行的关键因素。针对在不同神经网络结构下预测结果的准确性进行测试,计算期望输出与预测输出之间的平均绝对误差,确定BP神经网络模型的网络结构为4-8-1。BP神经网络其他训练参数见表2。

表2 BP神经网络其他训练参数
2.3 遗传算法优化模型
遗传算法能够有效避免BP神经网络在训练过程中陷入局部最小点无法自拔,提高模型的预测精度。在遗传算法中,将评价个体在特定环境下优劣程度的数学函数称为个体的适应度函数,是遗传算法演化的驱动力和选择的标准,决定着遗传算法优化BP神经网络模型最终的优化结果。将BP神经网络模型的实际输出与期望输出之间的误差绝对值之和作为个体的适应度值,其计算公式如式(1)所示

式中,n为输出节点数,yi为第i个节点的实际输出,zi为第i个节点的期望输出。本模型采用的编码机制为实数编码,个体编码长度为49。遗传算法训练参数见表3,其中算术交叉取值为0.5;基本位变异取值为0.075。

表3 遗传算法训练参数
将样本数据输入至遗传算法优化的BP神经网络模型内进行训练,建立选区激光熔化316L不锈钢成形残余应力预测模型,GA-BP神经网络拓扑结构如图6所示。
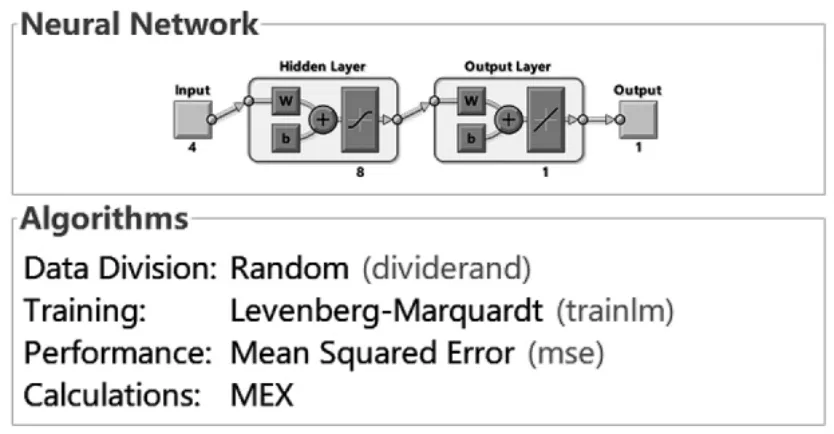
图6 GA-BP神经网络拓扑结构
迭代过程中种群里的最佳个体适应度值变化曲线如图7所示,从中可以看出随着种群个体之间不断地进行选择、交叉和变异操作,最佳个体适应度值呈现出阶梯下降的趋势,表明遗传算法在朝着正确的方向不断进化,并在第60代左右达到最小值,之后趋于稳定。

图7 最佳个体适应度曲线
选区激光融化316L不锈钢成形件残余应力预测结果如图8所示。由此看出,通过遗传算法优化BP神经网络能够得到实现良好预测精度。试验结果表明,其整体预测平均相对误差在5%左右,故建立的选区激光熔化316L不锈钢残余应力预测模型能够为后续工艺参数的优化提供良好的理论基础。

图8 神经网络模型残余应力预测结果
3 结束语
利用遗传算法优化BP神经网络的初始权值和阈值,构建选区激光熔化316L不锈钢成形残余应力预测模型。通过残差分析证明神经网络训练样本数据的可靠性,选择合理的适应度函数、遗传算子和种群规模等参数,进行GA-BP神经网络模型的学习训练,其整体预测平均相对误差在5%左右,证明通过人工神经网络模型实现选区激光熔化316L不锈钢成形残余应力预测的可行性。
