UHPC-T梁抗弯性能试验研究与理论计算

2023-01-31叶力豪

建筑科学与工程学报 2023年1期

朱琦，叶力豪，蔡玮，谢文

(宁波大学土木工程与地理环境学院，浙江宁波 315211)

0 引言

超高性能混凝土(Ultra-high Performance Concrete，UHPC)是一种具有超高抗压、抗拉强度和高韧性、高耐久性的新型水泥基复合材料，将其应用于桥梁结构中，可减轻结构自重，提高承载力和耐久性，具有广阔的应用前景[1-6]。尽管目前中国尚未制定UHPC桥梁设计规范，但不少学者已进行了较深入的研究。邓宗才等[7]研究表明：截面形式对UHPC梁的开裂荷载与延性影响甚大。傅元方[8]试验研究表明：UHPC梁的屈服和极限荷载受纵向配筋率的影响较大。孙小凯等[9]通过四点弯曲试验研究发现：纵筋配筋率不影响UHPC梁的开裂弯矩，但对其极限承载力的影响显著。Yang等[10]研究了配筋率和钢纤维体积掺量对梁受力性能的影响，结果表明：当钢纤维体积掺量不变时，纵向配筋率对UHPC梁的开裂性能无影响，对UHPC梁的极限承载力以及延性均有显著影响。Turker等[11]研究发现：当钢纤维体积掺量一定时，配筋率越大，UHPC梁的极限承载力越大，延性也更强，但超过一定配筋率时，对延性性能的改善作用减弱。梁兴文等[12]研究发现：纵向配筋率对UHPC梁的开裂荷载影响不大，但纵向配筋率可大幅提升UHPC梁的屈服荷载和极限荷载。彭飞等[13]考虑了钢纤维对UHPC受拉区的抗弯贡献，结果表明：钢纤维长度也是影响受拉区UHPC抗弯贡献的主要参数。曹霞等[14]开展了6根高强钢筋UHPC梁抗弯试验，研究了不同配筋率、纵筋等级、纵筋直径和受压钢筋直径对UHPC受力性能的影响规律。林明畅[15]设计制作了6组18根不同配筋率UHPC试验梁，探索了UHPC梁的适筋、超筋和少筋的破坏形态以及裂缝发展状态，推导了UHPC梁的开裂弯矩、极限弯矩和抗弯刚度计算公式。徐海宾等[16]在现行规范公式的基础上引入抗裂影响系数和裂缝修正系数，给出了UHPC梁的开裂弯矩和最大裂缝宽度计算公式。刘超等[17]在平截面假定基础上推导了配筋高应变强化的UHPC-T梁抗弯承载力计算公式，并与国外提出的计算方法进行对比，结果表明，所提出方法的计算值与试验值吻合度较高。李立峰等[18]进行了大比例预应力UHPC-T梁抗弯试验，改进了开裂荷载和极限荷载计算方法。徐海宾等[19]试验研究了6根预应力UHPC-T梁的抗弯性能，引入纤维长度修正系数和抗裂影响系数，对截面抵抗矩塑性影响系数进行修正，得到了预应力UHPC-T梁的开裂弯矩计算公式。

综上所述，目前的研究主要以矩形截面为主探讨UHPC梁的力学性能，而以预应力为主要影响因素研究其对T形截面抗弯性能的影响相对较少。本文以桥梁工程中的T梁为研究对象，制作4根UHPC-T梁(包括1根预应力UHPC-T梁)和1根普通混凝土T梁(对照梁)，研究配筋率和预应力对UHPC-T梁抗弯性能的影响；最后采用理论公式计算UHPC-T梁的开裂弯矩和极限弯矩等关键性能参数。

1 试验概况

1.1 模型制作及加载测点布置

由于受经费和试验场地等条件限制，足尺模型试验难以实现，因此采用缩尺模型开展相关研究工作。结合自身试验条件和研究目的，缩尺模型参照并改造了文献[20]中的试验模型，即调整了模型截面翼缘和腹板尺寸，但试验模型梁的抗弯和抗剪等性能均满足设计规范要求。UHPC-T梁的设计长度为2 400 mm，为防止两端发生锚固破坏，加载时两边预留了150 mm，计算跨度为2 100 mm，如图1(a)所示；T形截面的腹板尺寸为120 mm×150 mm，翼缘尺寸为280 mm×100 mm，如图1(b)所示。预应力UHPC-T梁的预应力采用后张法施加，在距梁底下缘56 mm处布置1根直径15.2 mm的预应力钢铰线，如图1(c)所示；其中锚垫板采用10 mm厚钢板以防止锚固区局部压碎，张拉预应力为110 kN。试验T梁的具体分组见表1，试验主要考虑配筋率和预应力等影响，其中普通混凝土T梁为对照梁。

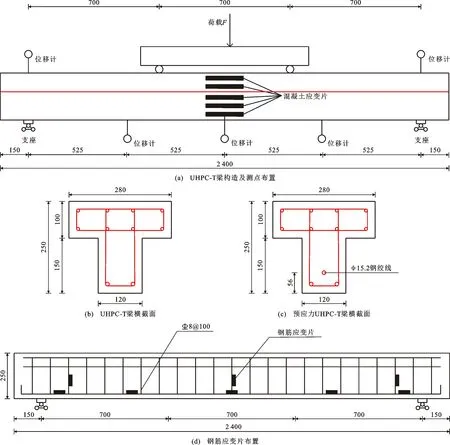
表1 T梁试验分组Table 1 T-beam test group

UHPC-T梁的制作采用常规的施工工艺，即先支模、绑扎钢筋、后浇筑UHPC和自然条件养护，现场作业如图2所示；试验采用的UHPC中水泥、硅粉、石英砂、水胶比的配合比为1∶0.5∶1.5∶0.18，且添加了2%的减水剂和体积掺量为2%的钢纤维。

自然条件下养护28 d达到龄期后，采用三等分点进行抗弯加载试验(图3)，通过分配梁将荷载对称分配到梁的两个三分点处，中间为纯弯段。试验加载仪器为结构疲劳试验系统PWS-250，试验开始前先预加载，如无异常，则卸载到0 kN再开始正式加载。试验加载采用分级加载，在达到使用状态试验荷载值Fs之前，每级加载值不超过0.10Fs，接近开裂荷载时，每级加载值不超过0.05Fs。开裂后每级加载控制为10 kN，UHPC-T梁到80 kN后改用位移1 mm·min-1控制加载直至梁破坏；普通混凝土梁到20 kN后改用位移1 mm·min-1加载直至梁破坏。

测试内容包括：竖向位移、混凝土应变、钢筋应变、裂缝等。①位移测试：沿梁安装5个竖向位移计(含两端支座处位移计)，如图1(a)所示。②应变测试：布置钢筋应变片用于测试箍筋和纵筋应变，如图1(d)所示；在梁跨中沿梁高布置5个混凝土应变片测试混凝土应变沿梁高的分布规律，如图1(a)所示。③裂缝测试：利用裂缝观测仪测量每个荷载步下最大裂缝宽度，并利用记号笔标记裂缝发展情况。

1.2 材料力学性能

1.2.1 UHPC力学性能

浇筑UHPC试验简支梁时，同时制作了3个边长为100 mm的立方体试件以测试其抗压强度，制备了3个100 mm×100 mm×300 mm长方体试件用于测试其弹性模量。浇筑了3个100 mm×100 mm×400 mm长方体试件以测试其抗弯折强度，加载装置见图4(a)；加工了3个180 mm×25 mm×25 mm狗骨形试件用于测试轴心抗拉强度，测试装置见图4(b)。所有试件与UHPC试验简支梁的养护条件相同，测得的力学性能如表2所示。

表2 UHPC与C40混凝土力学性能Table 2 Mechanical properties of UHPC and C40 concrete

1.2.2 钢筋力学性能

按照《金属材料室温拉伸试验方法》[21]规定进行钢筋拉伸试验。所得的钢筋物理力学性能指标如屈服强度、极限强度等见表3。

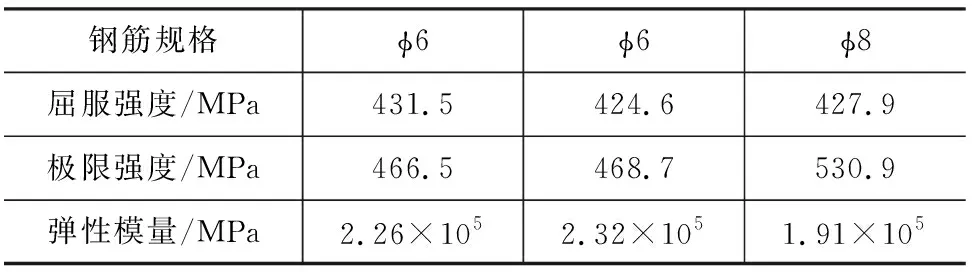
表3 钢筋力学性能Table 3 Mechanical properties of reinforced rebars

2 配筋率对UHPC-T梁抗弯性能的影响

2.1 裂缝分布与抗裂性能

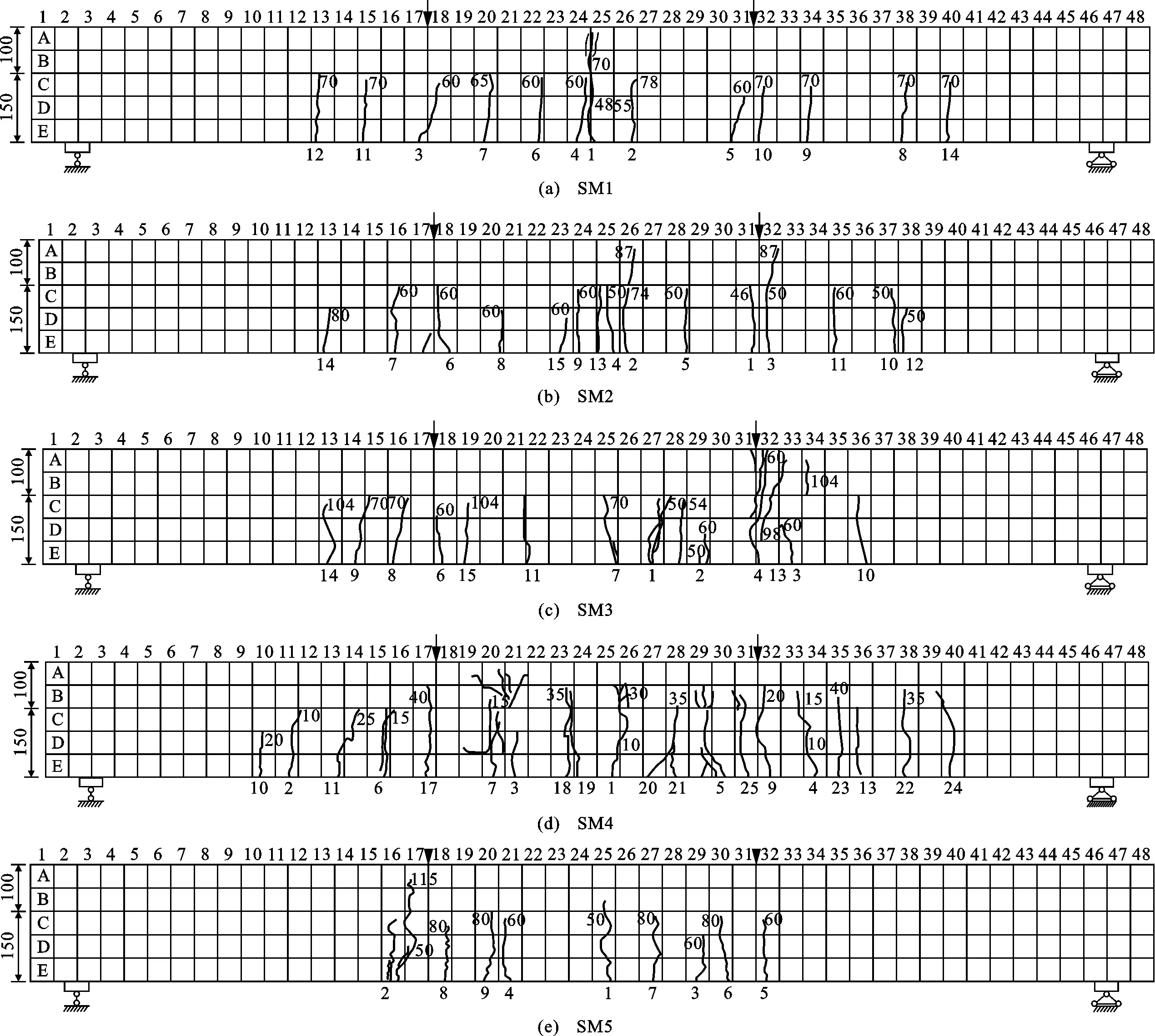
各模型梁的裂缝分布如图5所示，其中裂缝中数字为裂缝发展位置对应的荷载，单位为kN。由图5可以看出，各试验梁裂缝分布有如下特点：①相比SM4梁，SM1、SM2、SM3梁的裂缝出现较晚，且发展速度较慢；②SM1、SM2、SM3梁翼缘上裂缝较少，主要集中在加载点附近，而SM4梁翼缘上有较多裂缝且穿过翼缘向上发展；③SM1、SM2、SM3梁裂缝数量远小于SM4梁，表明钢纤维可阻碍裂缝发展，使裂缝分布更加均匀。从图5还可看出，SM1、SM2、SM3梁的裂缝发展特征为：随着荷载的增加，裂缝宽度逐渐变大，裂缝不断向上扩展；当荷载持续增加时，梁的裂缝数量和宽度逐渐增大，并能听到受拉区混凝土内钢纤维被拔出的声音，但直到试验由于破坏而停止，其受压区混凝土未被压碎。

裂缝对结构的刚度和耐久性产生显著影响，图6给出了各模型梁的荷载与最大裂缝宽度关系。与SM3梁相比，SM1、SM2梁由于其配筋率较低，初裂过后它对裂缝宽度的限制作用有限，导致开裂过后裂缝发展迅速，比如SM1、SM2、SM3梁的开裂荷载对应的最大裂缝宽度均为0.01 mm，而加载至80 kN时对应的最大裂缝宽度分别为0.22、0.26、0.08 mm，表明提高配筋率可阻止UHPC-T梁裂缝的发展。当配筋率从0.209%提高至0.744%，SM1梁和SM3梁极限荷载对应的最大裂缝宽度从1.92 mm降至1.56 mm，表明提高配筋率可以增大梁的抗裂性能和安全性能。SM2梁和SM4梁最大裂缝宽度均为0.01 mm时，对应的开裂荷载分别为46 kN和10 kN，当SM4梁加载至20 kN时，其最大裂缝宽度已扩大至0.18 mm，表明UHPC可阻止T梁裂缝的发展和提升梁的抗裂性能和承载能力。

2.2 混凝土应变

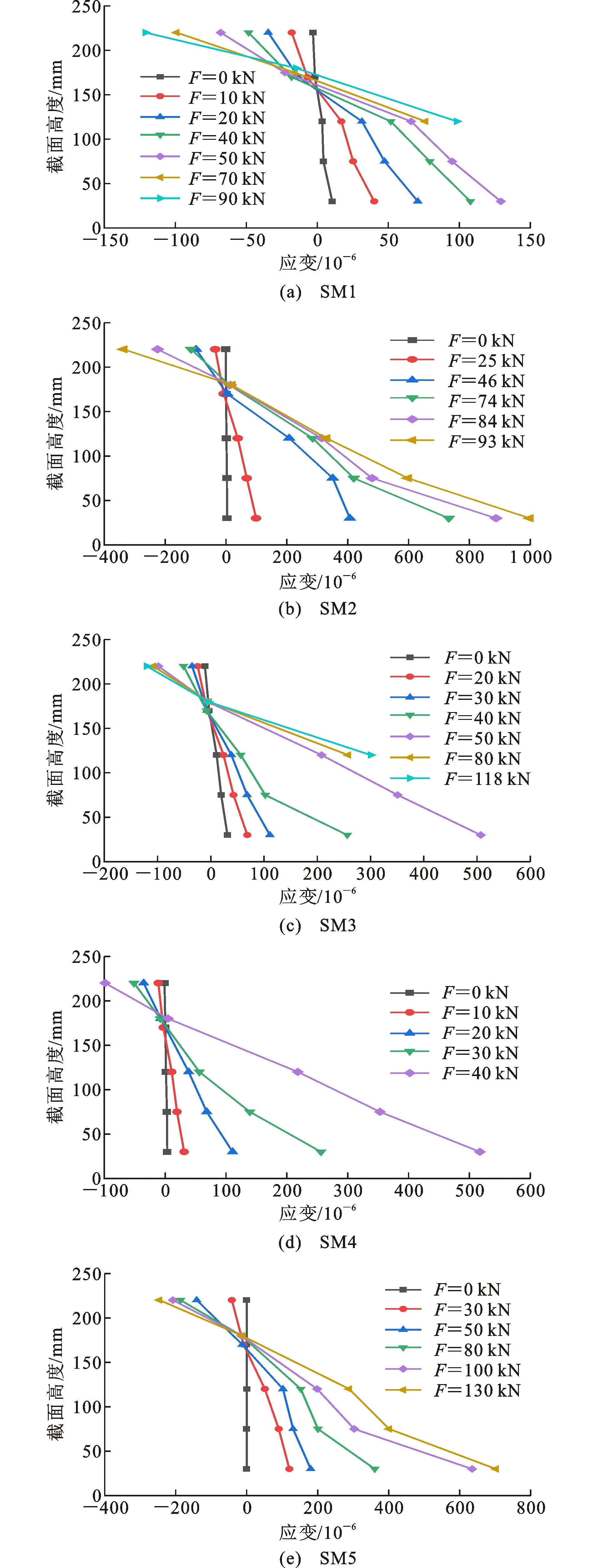
图7为不同荷载下各模型梁混凝土应变沿梁高的分布规律。由图7可以看出：UHPC-T梁或普通混凝土T梁在开裂前处于弹性阶段，中性轴位置基本保持不变，表明T形截面满足平截面假定；UHPC-T梁或普通混凝土T梁开裂后，其中性轴位置出现逐渐上升。此外，部分测点出现突变，主要是由于该位置出现了裂缝所致。

2.3 荷载-跨中位移曲线

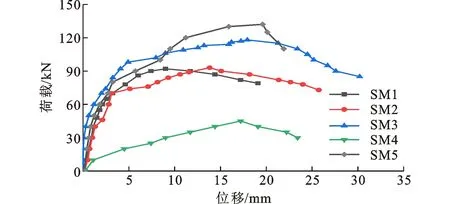
图8给出了各模型梁荷载-跨中位移曲线。与SM4梁类似，SM1、SM2、SM3梁经历了弹性阶段、裂缝开展阶段和破坏阶段3个不同受力阶段。SM1、SM2、SM3梁的开裂荷载分别为48、46、50 kN，表明配筋率对UHPC-T梁的开裂弯矩影响不大，两者最大相差约8.7%，这是因为UHPC-T梁的开裂弯矩取决于UHPC水泥基体的抗拉能力。当配筋率从0.209%增加至0.744%，相应的极限荷载由92 kN提高至118 kN，增大了28.3%，表明配筋率的增加明显提高了UHPC-T梁的极限承载力。此外，比较SM1梁和SM2梁可知，两者的极限荷载非常接近，分别为92 kN和93 kN，表明UHPC-T梁为少筋梁时，提高配筋率不会提高其极限承载力，主要是因为少筋梁的极限承载力由受压区混凝土控制。

3 预应力对UHPC-T梁抗弯性能的影响

3.1 裂缝分布与抗裂性能

从图5中SM2、SM5梁的裂缝分布可以看出，SM5梁(预应力UHPC-T梁)与SM2梁(UHPC-T梁)相比，裂缝分布有如下特点：①试验梁首先在跨中部位出现第一条裂缝，随着荷载继续增加到80 kN，裂缝主要集中在加载点附近，非纯弯曲段裂缝相对较少；②随着荷载继续增加到115 kN，除加载点外并未产生新的裂缝；③与SM2梁相比，SM5梁裂缝数量和主裂缝宽度都明显减小，表明施加预应力可以有效减少裂缝宽度和数量。从图5(b)、(e)可以看出，SM5梁的裂缝发展特征为：随着荷载的增加，裂缝宽度逐渐变大，裂缝不断向上扩展，但是少有裂缝发展到翼缘部分；当荷载持续增加时，梁的裂缝数量和宽度逐渐增多，裂缝中不断有UHPC粉末掉下来，并伴随有钢纤维断裂的声音，但直到试验由于破坏而停止，其受压区混凝土未被压碎。

从图6给出的SM2梁和SM5梁的荷载与最大裂缝宽度关系可以看出，与SM2梁相比，SM5梁由于施加了预应力，初裂过后其对裂缝宽度有限制作用，使得开裂过后裂缝发展缓慢，比如SM2和SM5梁的开裂荷载对应的最大裂缝宽度均为0.01 mm，而加载至80 kN时对应的最大裂缝宽度分别为0.26 mm和0.12 mm，表明施加预应力可以阻止UHPC-T梁裂缝的发展。此外，SM2和SM5梁极限荷载对应的最大裂缝宽度从1.85 mm降至1.41 mm，表明施加预应力可以增大梁的抗裂性能和安全性能。

3.2 混凝土应变

从图7(b)、(e)给出的不同荷载下SM2梁和SM5梁混凝土应变沿梁高的分布规律可以看出：UHPC-T梁和预应力UHPC-T梁在开裂前处于弹性阶段，其中性轴位置基本保持不变，表明T形截面满足平截面假定；UHPC-T梁和预应力UHPC-T梁开裂后，其中性轴位置出现逐渐上升。此外，部分测点出现突变，主要是由于该位置出现了裂缝所致。

3.3 荷载-跨中位移曲线

从图8中的SM2、SM5梁荷载-跨中位移曲线可以看出，SM5梁与SM2梁类似，经历了弹性阶段、裂缝开展阶段和破坏阶段3个不同受力阶段。SM2、SM5梁的开裂荷载分别为46 kN和50 kN，两者相差约8.7%，表明施加预应力对UHPC-T梁的开裂弯矩影响不大，这是因为UHPC-T梁的开裂弯矩取决于UHPC水泥基体的抗拉能力。由于SM5梁施加了预应力，相应的极限荷载由93 kN提高至132 kN，增大了42%，表明施加预应力可以明显提高UHPC-T梁的极限承载力。

4 理论计算

根据截面应力分析法，分别计算普通混凝土和UHPC-T梁的开裂弯矩Mcr和极限弯矩Mu[16-17]。

开裂弯矩：

Mcr=(σp+γft)W0

(1)

(2)

λr=ρflf/df

(3)

式中：γ为截面塑性抵抗系数；βf为抗裂影响系数；λf为钢纤维含量特征值；ρf为钢纤维体积率；lf为钢纤维长度；df为直径；ft为UHPC轴心抗拉强度；W0为换算截面对截面受拉边缘的弹性抵抗矩；S0为换算截面计算纤维以上或以下部分面积对截面重心轴的面积矩；σp为预应力在构件抗裂边缘产生的预压应力。

根据公式(1)～(3)得到各T梁的理论开裂弯矩，列于表4中。

极限弯矩：

(1)若T形截面特性符合公式(4)，中性轴在翼缘内，考虑腹板受拉区UHPC的抗拉作用，按公式(5)进行正截面抗弯承载力Mu计算。

(4)

(5)

UHPC受压区高度应按式(6)计算。

表4 各模型梁开裂弯矩理论值与试验值对比Table 4 Comparisons between computational and experimental values of cracking-resistance moment of model beams

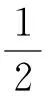
(hf-x)+fpyAp

(6)

(2)当不符合公式(4)时，中性轴在腹板内，应考虑截面中腹板的受压作用，其正截面抗弯承载力应按式(7)计算。

(x-hf)2+fpyAp(h0-ap-x)

(7)

UHPC受压区高度按式(8)计算。

fyAs+βftdb(h-x)+fpyAp

(8)

式中：β为受拉区UHPC等效矩形应力系数；fcd为UHPC轴心抗压强度设计值；fck为UHPC轴心抗压强度标准值；ftd为UHPC轴心抗拉强度；As为受拉钢筋总面积；fy为钢筋屈服强度；fpy为预应力筋抗拉强度设计值；AP受拉区纵向预应力筋的截面面积；ap为受拉区纵向预应力筋合力点至截面受拉区边缘的距离；hf为翼缘高度；h为截面高度；h0为截面有效高度；bf为翼缘宽度；b为腹板宽度；x为受压区高度。

通过计算，试验梁受压区高度x在翼缘hf内，适用于公式(4)，根据公式(5)得到相应的计算结果(表4)。由表4可知：UHPC-T梁的开裂弯矩试验值与理论值的比值在0.81～0.89之间，相应的比值均小于1，最大相对误差为18.6%；其主要原因是本文计算公式采用的抗裂影响系数βf主要与钢纤维掺量及种类有关，且与钢纤维掺量成正比，同时它是根据钢纤维质量分数为3%的试验数据回归得到[16]，导致公式(1)针对本文钢纤维质量分数为2%的试验模型的计算结果偏大。UHPC-T梁(SM1～SM3)的极限弯矩试验值与理论值的比值从1.054降至0.811，最大相对误差为11.9%，其原因是本文公式计算采用的受拉区UHPC等效矩形应力系数β取0.90，它主要与配筋率有关，且随着配筋率增大而逐渐减小，导致采用公式(5)计算的理论极限弯矩随配筋率的增大而增大，即配筋率从0.209%(SM1)增大至0.744%(SM3)，相应的试验值与理论值的比值从1.054降至0.811。因此，SM2和SM3的极限弯矩理论值大于相应的试验值。