金属地下矿山深部转产过程中的产能接续优化

侯 杰，李国清✉，修国林，胡乃联，强兴邦

1) 北京科技大学土木与资源工程学院，北京 100083 2) 金属矿山高效开采与安全教育部重点实验室，北京 100083 3) 山东黄金集团有限公司，济南 250013

近年来，随着我国对于金属矿产资源需求的不断增长，矿山产能规模持续扩大，浅部地质资源被迅速消耗，越来越多的矿山进入深部开采[1-3]，以达到扩大产能、产生规模效益的目的，因而已普遍形成了多区段联合开采的复杂生产格局.然而，在这种复杂生产格局下，无论是新增深部矿体生产能力的形成，还是原有生产区域资源的可持续利用，都需要制定合理的生产规划[4-7]，否则将造成过渡时期出现减产或停产过渡现象.因此，如何依据科学的方法对矿山的产能接续进行规划优化，是我国矿山企业在深部转产过程中一项亟待解决的问题.

目前，国内学者多采用统计分析、技术分析、经济分析和综合因素分析等方法[8-12]，通过对露天转地下过渡期的生产规模进行优化，以解决矿山整体产能的平稳接续与均衡过渡等关键技术问题[13-16].而在地下矿山进行深部开采时的产能接续问题研究中，已有学者开始使用线性规划的方法[17-19]，合理确定矿井的持续生产能力，并实现新增矿区和原有生产区域的协同开采[20-22].其中金京男[23]针对焦家金矿的生产接续问题，根据双品位滚动优化原理，采用线性规划的方法建立相关数学模型，通过对多区段矿山生产进行合理优化，从而达到矿山稳产的目的，同时实现了对矿山资源的综合利用.徐海[24]以全矿计划出矿品位与选厂合理入选品位偏差最小为目标函数，构建了资源开采线性规划模型，并采用MATLAB软件，实现了凡口铅锌矿各区段和各中段的资源开采规划，对促进矿山持续稳定发展、合理开采现有资源具有重要现实意义.

总体来看，目前关于矿山产能接续问题的研究大多侧重于露天转地下的不停产过渡.而针对地下矿山由浅部转入深部的产能接续问题研究较少，忽略了多矿区发展不协调所带来的资源浪费和经济效益损失.为此，本文以山东黄金矿业(莱州)有限公司三山岛金矿为工程背景，结合深部开采初步设计所给出矿区开发方案，全面规划矿山产能分配.通过以多矿区资源综合开采价值最大为优化目标，综合考虑客观开采约束条件，展开地下矿山深部转产过程中产能接续规划优化模型的研究，在时间维度上实现逐年度生产能力的平衡过渡，为我国具备同样工程背景的矿山提供模型与方法上的借鉴和参考.

1 深部转产过程中的产能接续性问题分析

1.1 三山岛金矿深部开采新格局

三山岛金矿作为山东黄金的骨干矿山，承担了重要的生产任务，其金金属产量约占全集团的1/6左右，并且随着深部工程的形成，矿山的开采能力得到进一步提升.三山岛金矿深部延伸与开采工程于2018年启动，根据矿产资源开发利用可行性研究推荐设计方案，计划经过7年的基建期，矿山的整体产能将由现在的10000 t·d-1扩展至15000 t·d-1.这要求在深部延伸建设期内，矿山的生产产能由现在的西山、新立矿区平稳过渡到深部西岭矿区，西岭矿区在第5、6、7年分别达到预期产能的40%、60%和80%，并于第8年达到预期产能，同时选厂于第8年完成扩建工程，达到设计选矿能力.三山岛金矿深部延伸工程完成后的矿石流向示意图，如图1所示.

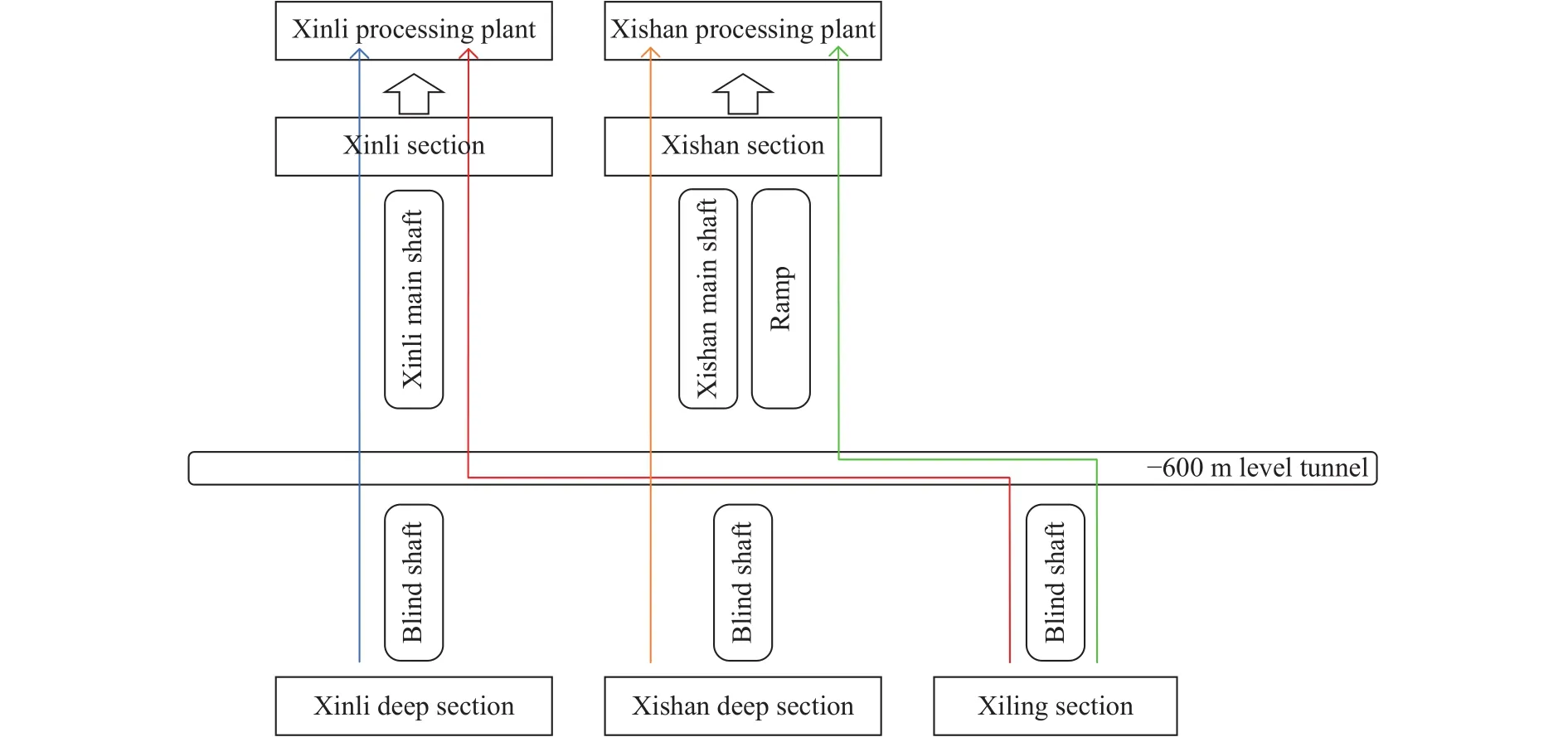
图1 三山岛金矿矿石流向示意图Fig.1 Schematic of the ore flow direction for Sanshandao gold mine

按照预期开采规划，矿山形成了五个矿区，分别为西山矿区、西山深部矿区、新立矿区、新立深部矿区和西岭矿区.西山矿区和西山深部矿区作为一个开采系统，矿石通过西山主井和斜坡道运出，西山开采系统设计矿石提运能力为1.65×106t·a-1；新立矿区和新立深部矿区作为一个完整的开采系统，矿石通过新立主井运出，新立开采系统设计矿石提运能力为 3.3×106t·a-1；西岭矿区作为一个独立的开采系统，采下矿石通过盲竖井提运至-600 m大巷，盲竖井设计矿石提运能力为3.3×106t·a-1，提出矿石转运至西山和新立主井提升至地表，因此，西岭矿区的矿石提运将占用西山和新立开采系统的提运能力.在选矿系统上，最终形成新立选矿厂的生产能力为330×104t·a-1，西山选矿厂的生产能力为 1.65×106t·a-1.

1.2 产能接续规划优化基本原则

针对上述矿山深部转产过程中的产能接续性需求进行分析可知，产能接续规划优化的最终目标是得到符合实际生产的最佳产能接续与生产任务分配方案，其中具体的优化原则主要包括：

(1) 必须根据矿山企业的实际情况，确定与各矿区资源赋存条件及开采技术条件相适应的生产能力和开采强度，以实现多矿区的协同开采，并保证矿山在浅部与深部接续开采的过渡期内产能均衡稳定.图2展示了三山岛金矿各矿区资源赋存条件，目前主要采用上向水平分层充填采矿法进行开采.

图2 各矿区资源赋存条件Fig.2 Resource condition of each mining section

(2) 必须正确处理矿石产量和金属产量两者之间的关系，保证矿石入选品位满足企业生产的需求.

(3) 矿山企业的最终目标是获取最大利润，矿山生产成本的高低制约着企业的经济效益，因而产能接续规划优化必须满足矿山生产成本最低的原则，以保证整个规划期内多矿区协同开采的经济效益最大化.

2 深部转产过程中的产能接续性问题分析

2.1 问题定义

以三山岛金矿深部转产的设计方案为例，并根据深部转产过程中产能接续性问题分析，针对产能接续规划优化模型可以描述如下：各个矿区采出的矿石可经由一个或多个生产系统提升运输，送至与各生产系统所对应的选厂进行矿石处理，最终得到金属产品，如图3所示.在这个过程中，金属产品的产量主要受各矿区生产能力、关键提运能力、矿石处理量的限制.其中，关键提运能力的限制在于各生产系统的最大提升能力；矿石处理量的限制在于各生产系统所对应选厂的最大矿石处理能力.同时，结合矿山开采实际情况，还需要对模型做出如下假设.

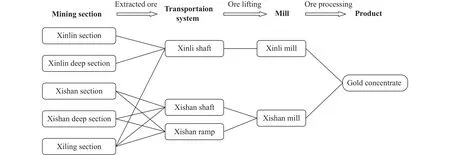
图3 多矿区同时开采的矿石流图Fig.3 Ore flow diagram of simultaneous mining in multiple sections

(1) 由于矿床的地质构造差异，模型将各个矿区作为独立个体进行考虑，各矿区均有与之相匹配的技术经济参数.

(2) 矿山进行深部资源开采时为产生规模效益需要提升整体的生产能力，因而需要对选厂进行改扩建.但由于选厂的改扩建工程进度较快，模型中暂不考虑其对矿山生产的影响.

(3) 模型中仅考虑各矿区总生产能力和提升能力，不对各中段生产、运输能力进行要求.

2.2 目标函数

(1) 收入最高.在进行产能接续规划优化时，需要依据金属的市场价格，考虑各矿区开采所能带来的经济价值，合理分配各矿区的生产任务，以达到矿山生产的最大收入，其数学表达式为：

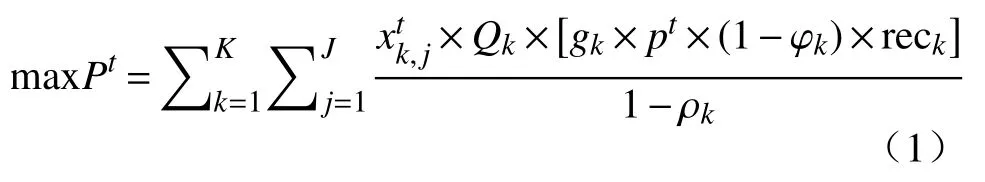
式中：k为西山矿区、新立矿区、西山矿区深部、新立矿区深部和西岭矿区；j为西山主井、西山斜坡道和新立主井代表的生产系统；为 第t年 第k个矿区送至第j个生产系统的矿石量所占第k个矿区保有储量的比例(%)；Qk为第k个矿区的矿石保有储量(t)；gk为第k个矿区的矿石平均品位(g·t-1)；pt为第t年的黄金市场价格(¥·g-1)； φk为第k个矿区的采矿损失率(%)； ρk为第k个矿区的矿石贫化率(%)；reck为选矿回收率(%).

(2) 生产成本最低.矿山的生产成本包括采矿成本、选矿成本以及运输成本，其中各项成本指标均与矿石产量有着直接的关联.因而将各矿区作为一个整体计算生产成本，处于同一矿区的单位矿石生产成本相同，则矿山生产成本最低目标的数学表达式为：

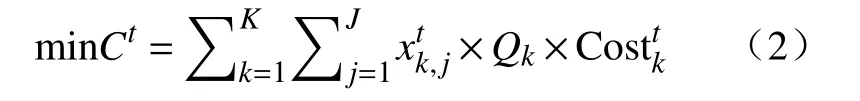
因此，产能接续规划优化的目标即为规划期内多矿区资源综合开采价值最大化，则在贴现率为i的情况下目标函数如下：

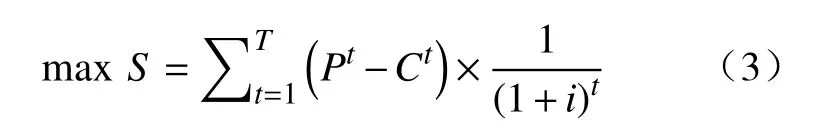
式中：S为开采总净现值收益(¥)；i为贴现率(%)；其余同上.

2.3 约束方程

在建立产能接续规划优化模型过程中还需要考虑诸多约束条件的限制，以控制模型优化结果满足矿山实际生产的产量和质量要求.约束条件涉及的变量应能够充分反映矿山实际生产运营过程中的主要指标参数.为实现矿山整体生产能力的稳定持续、确保矿石供需平衡，建立约束条件数学表达如下:

(1) 最大提升能力约束.提升设备的提升能力决定了矿山整体的出矿能力，为了避免大量矿石堆积，第j个生产系统的提升矿石量不能超过其预设的最大提升能力，建立数学表达式为：

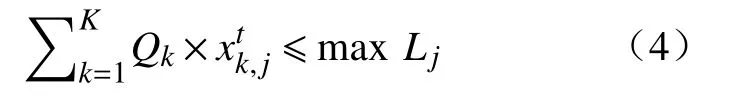
式中： m axLj为第j个生产系统的最大矿石年提升能力 (t·a-1).

(2) 最大选矿能力约束.考虑选矿设备能力、人员数量、材料供给等因素的限制，第j个生产系统所对应选厂的最大矿石处理量不能超过其预设的最大矿石处理能力.数学表达式为：

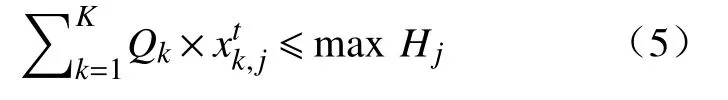
式中： m axHj为第j个生产系统所对应选厂的最大矿石年处理能力(t·a-1).

(3) 品位均衡约束.为了满足选厂对于矿石入选品位的要求，第j个生产系统提升矿石的平均品位应保证在一定范围内变化，否则会不符合选矿的工艺流程和技术，造成选矿回收率的降低.数学表达式为：

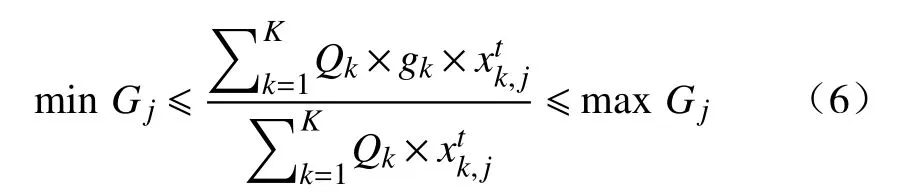
式中： m inGj为第j个生产系统所对应选厂的入选品位下限(g·t-1)； m axGj为第j个生产系统所对应选厂的入选品位上限(g·t-1).

(4) 产能均衡约束.针对新增深部矿区，各矿区的矿石产量应逐年递增；而针对原有生产矿区，各矿区的矿石产量应逐年递减.其公式为：

(5) 开采过渡期产能接续约束.西岭矿区在第5、6、7年分别达到预期产能的40%、60%和80%，并于第8年达到预期产能针对新增深部矿区，针对过渡期设置产能限制.其公式为：

式中：k=西岭矿区；D为西岭矿区设计产能(t·a-1)；nt为第t年的达产比例.

(6) 决策变量约束.第k个矿区的矿石采出总量应不超过其总矿石储量，即：

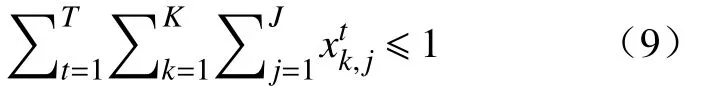
3 模型的应用

3.1 矿山开采技术经济参数

为了验证模型在深部转产过程中产能接续规划优化应用中的可行性，将上述模型应用于三山岛金矿的深部开采规划.在此之前，需要结合三山岛金矿的工程实际，对模型中涉及的相关参数进行技术，估算各矿区的技术经济与生产系统能力限制等模型关键参数如表1所示.

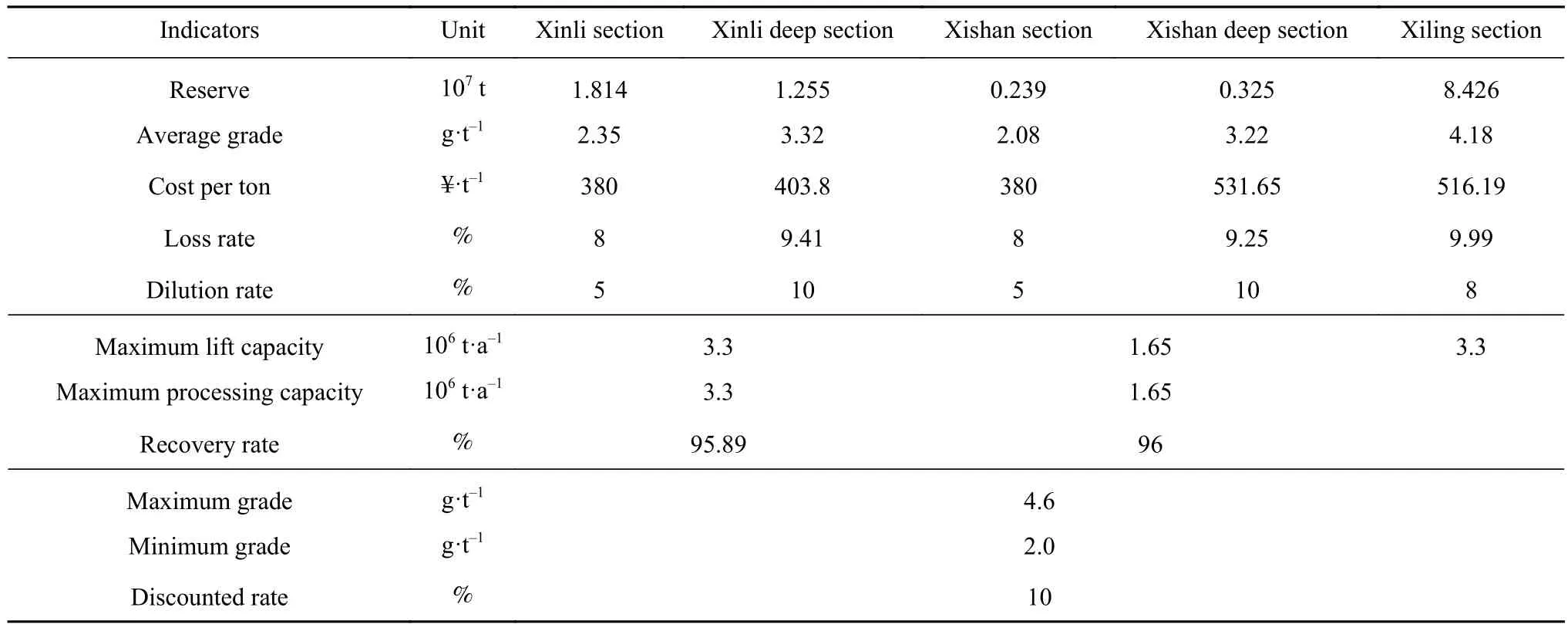
表1 开采技术经济指标表Table 1 Mining technical and economic parameters

针对金属价格的估计，以近十年月度黄金现货交易价格为数据基础，运用Eviews软件对黄金价格进行随机过程拟合，得到黄金价格服从均值回归运动的随机过程，在此基础上，运用Matlab进行蒙特卡洛模拟，可以得到1000条黄金价格走势的预测结果.同时，对未来的黄金价格预测结果按年均值进行统计，如表2所示.

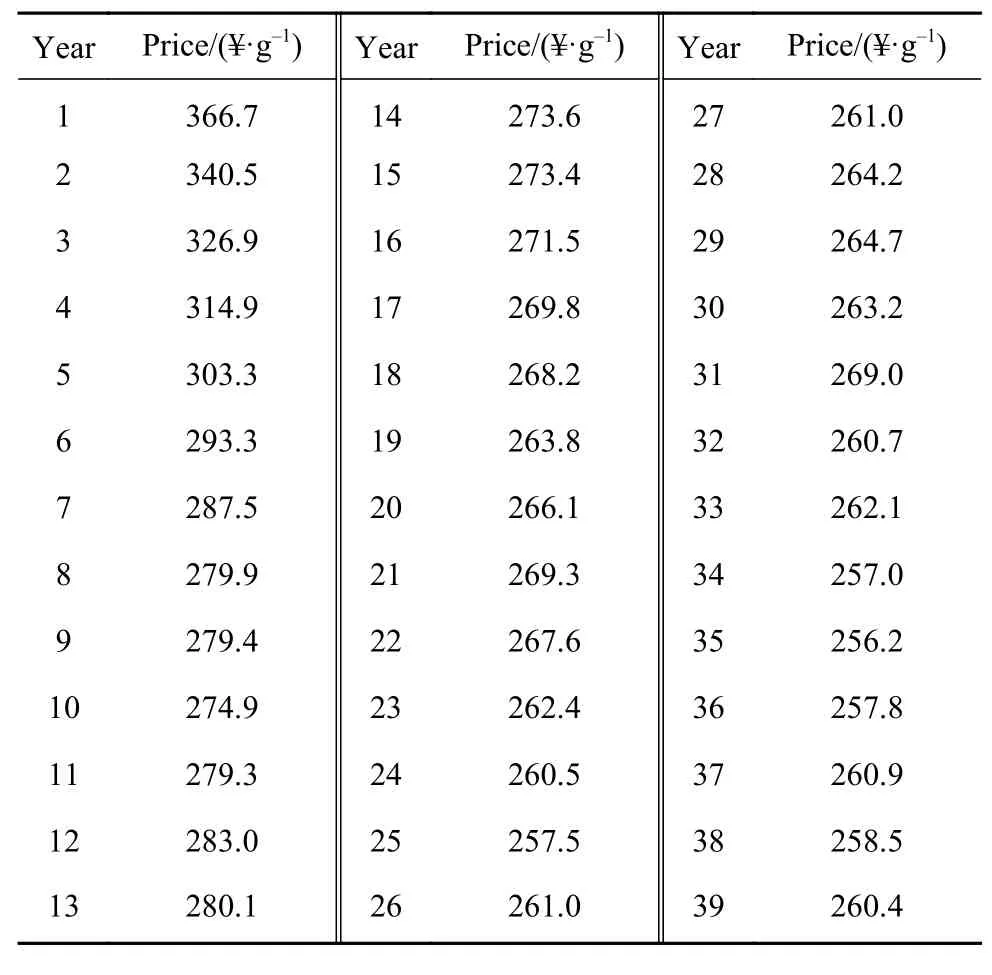
表2 基于均值回归运动模型的黄金价格预测结果Table 2 Prediction results of gold price based on the mean regression motion model

3.2 数据处理与模型求解

在代入上述技术经济参数与预测的黄金价格对本文所构建的产能接续规划优化数学模型进行求解的过程中，由于该模型具有变量多、开采生命周期长、约束条件复杂等特点，导致了模型求解难度大，周期长等问题.因而需要适用于求解大型线性规划问题的求解方法及工具.因此，本文选择在Python和Gurobi的建模环境下，结合三山岛金矿的实际情况，对产能接续规划优化模型进行求解，具体流程如图4所示.

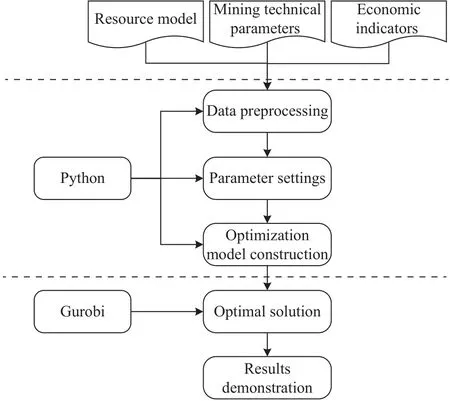
图4 Python和Gurobi建模环境下的模型求解流程Fig.4 Modeling and solving process in Python and Gurobi software

3.3 优化结果分析

图5～图8统计了三山岛金矿产能接续规划优化模型的解算结果，分别对图中的统计结果进行分析，可以得到以下结论.

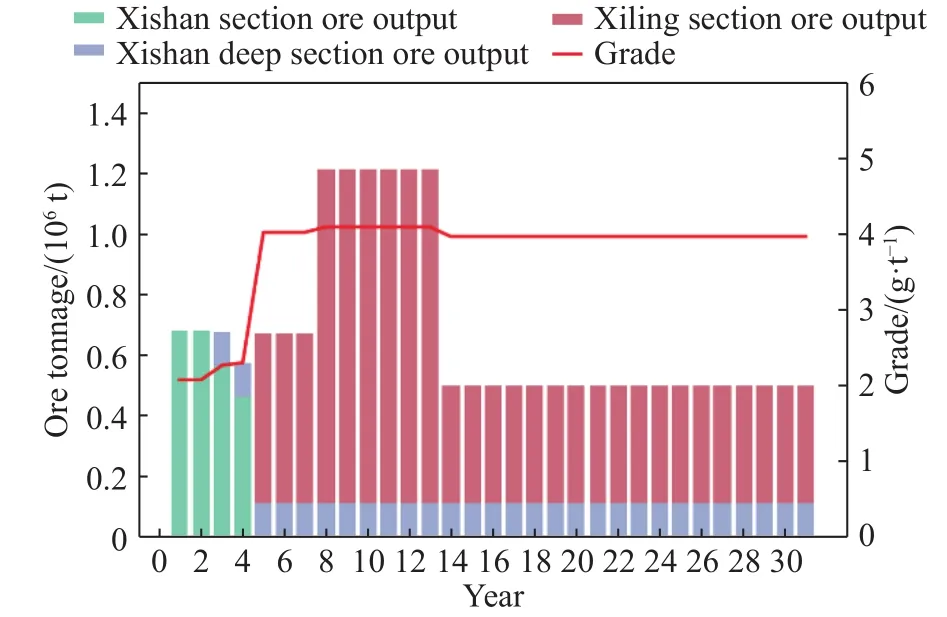
图8 规划期内西山选厂矿石处理量、入选品位结果统计Fig.8 Processing capacity and ore grade per year of Xishan processing plant during the planning period

(1)从图5中可以看出，第1至2年在产矿区为新立和西山矿区；第3至4年新立、西山以及西山深部同时开采，第4年西山结束开采；第5至13年新立、西岭、新立深部以及西山深部同时开采，第13年新立结束开采；第14至31年西岭、新立深部和西山深部同时开采.同时，各矿区年产量在稳产期均接近各自年生产能力的最大上限.但是，由于第14年新立和西山浅部矿体开采结束，西岭矿区又受限于盲竖井提升能力限制，已达到最大生产能力，而新立、西山的深部资源量较少，其年生产能力较小，因而导致全矿整体的矿石产量有所下降.

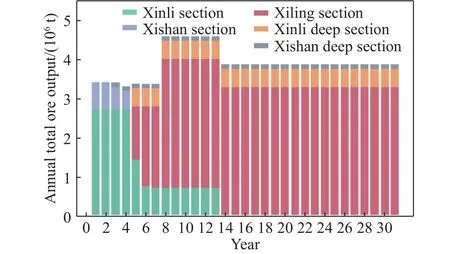
图5 规划期内各年各矿区矿石产量结果统计Fig.5 Annual ore output of each mining area during the planning period

(2)从图6中可以看出，规划期内各年各矿区净现金收益的变化情况与矿石量变化呈相似趋势.本开采方案是以预测价格作为基准得到的优化结果，若矿山开采过程中，黄金价格呈上涨趋势，图6显示的净现金收益会整体增加，并且后期收益下降幅度变缓，反之，若黄金价格呈下降趋势，图6所示的净现金收益会整体减少，并且后期收益下降幅度变大.

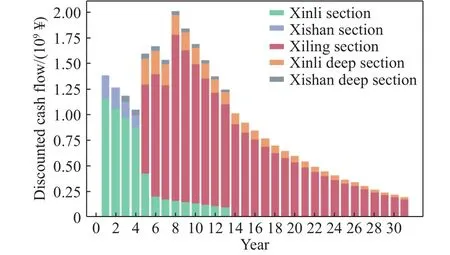
图6 规划期内各年各矿区净现金收益结果统计Fig.6 Annual net present value of each mining area during the planning period

(3)从图7中可以看出，新立矿区、新立深部矿区以及西岭矿区部分矿石被提运至新立选厂进行选矿处理.在第1至4年，主要矿石来源为新立矿区；第5至13年，主要矿石来源为新立、新立深部以及西岭矿区，第13年新立矿区结束开采；第14至31年主要矿石来源为新立深部以及西岭矿区；其中第8至31年，新立选厂达到了最大矿石处理能力.在矿石平均入选品位方面，第1至4年，由于主要开采的新立矿区矿石平均品位较低，新立选厂入选品位在2.35 g·t-1左右.从第5年起至13年，随新立深部矿区和西岭矿区矿石的混入，入选品位逐渐增加至3.67 g·t-1左右.第14年以后，随新立矿区低品位矿石开采结束，西岭矿区更多高品位的矿石被开采，新立选厂入选品位进一步提高至 4.06 g·t-1.

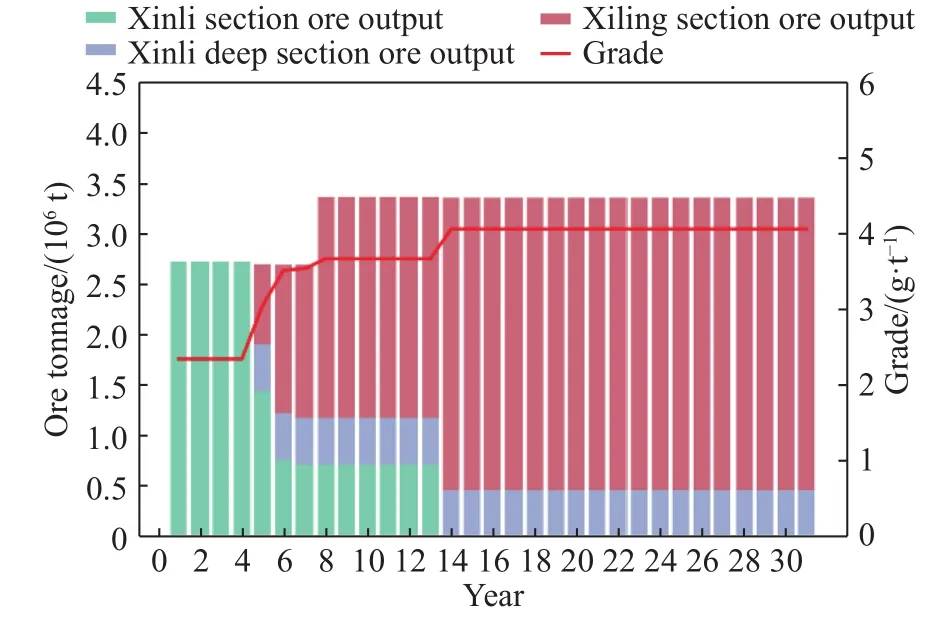
图7 规划期内新立选厂矿石处理量、入选品位结果统计Fig.7 Processing capacity and ore grade per year of Xinli processing plant during the planning period

(4)从图8中可以看出，西山矿区、西山深部矿区以及西岭矿区部分矿石被提运至西山选厂进行选矿处理.在第1至2年，主要矿石来源为西山矿区；第3至4年，主要矿石来源为西山、西山深部矿区，第4年西山矿区结束开采；第5至31年，主要矿石来源为西山深部和西岭西山深部.受生产系统的整体提运能力限制，西山选厂在整个规划期内都不超过最大选矿处理能力.在矿石平均入选品位方面，第1至2年，由于主要开采的西山矿区矿石平均品位较低，西山选厂入选品位在2.08 g·t-1左右.第3至4年，随西山深部矿区矿石的混入，入选品位逐渐增加至2.30 g·t-1左右.第5年以后，随西山矿区低品位矿石开采结束，西岭矿区更多高品位的矿石被开采，西山选厂入选品位进一步提高至4.00 g·t-1左右.

综合以上结果分析可知，在三山岛金矿进行深部转产的过程中，基于上述所构建的产能接续规划优化模型优化得到的产能接续与生产任务分配方案，可以在满足产能均衡、品位均衡与各项生产系统能力限制等约束条件的基础上，实现多矿区的协同开采，促进矿山生产经营效益的提升，验证了优化模型的科学性和有效性.

4 结论

(1)通过深入剖析矿山深部转产过程中的产能接续性问题，提出了以多矿区资源综合开采价值最大为目标和以产能均衡、品位均衡与各项生产系统能力限制为约束条件的产能接续规划优化数学模型.

(2)三山岛金矿开采过渡期将面对多个生产区域同时供矿的复杂生产条件，通过优化模型得到了多矿区在时间和空间上的协同和接续方案，在保证矿山生产目标达成和经济效益持续稳定的前提下，实现了现有产能向新增产能的平稳有序过渡.

(3)将模型应用于三山岛金矿深部开采规划，结果表明本文所构建的产能接续规划优化模型保证了接续期的产能平衡过渡，同时也解决了三山岛金矿深部生产系统形成后的多矿区协同生产问题，有效提升矿山收益.