面向不确定数据的序数回归算法
2023-01-31肖燕珊
李 晰,肖燕珊+,刘 波
(1.广东工业大学 计算机学院,广东 广州 510006; 2.广东工业大学 自动化学院,广东 广州 510006)
0 引 言
序数回归 (ordinal regression,OR)问题与传统的多分类学习问题[1]的根本区别在于:不同分类结果之间是否具有顺序性。序数回归模型广泛应用于不同的领域,例如协同过滤、信息检索、信用评级和医学研究等。
为了提高序数回归模型分类效果,本文在支持向量有序回归的基础上做了相关改进。通过本文所提出的面向不确定数据的支持向量机序数回归模型(support vector ordinal regression based on uncertain data, USVOR),可以减少不确定信息对序数回归模型的影响,提高模型的鲁棒性。本文的主要贡献有3个方面:
(1)通过建立不确定性数据的模型,减少外界环境产生的不确定数据对序数回归模型的影响。
(2)把不确定数据模型融合到序数回归算法中,设计面向不确定数据的支持向量机序数回归模型,并给出求解方法。
(3)在真实数据集的实验结果表明,相比现有的序数回归算法,我们算法具有更好的鲁棒性。
1 相关工作
根据研究人员的不同构建方式,本文可将现有的序数回归分为三大类:
(1)朴素方法,将序数回归问题作为标准的分类问题或传统的回归问题,并结合机器学习算法来提高序数回归的性能。Xiao等[2]提出了基于支持向量机 (support vector machine, SVM)和多示例学习的方法来处理多分类问题,其中的标签按顺序进行排列,数据采用的是多实例的形式。李亚克等[3]通过大量离散样本来构建缓变类内散度矩阵,从而获取样本数据中准确的时间序列,基于有序条件的约束和线性判别规则获取最佳的映射,进而可以训练得到有序数据。马闯等[4]也引入有序信息,并基于最小平方回归的方法对序数回归函数中的标号改造来扩大分类间隔。其中,序数回归中的朴素方法可结合机器学习算法来训练模型,目前结合相关的机器学习主要有最小二乘法回归、回归树、支持向量机等内容。
(2)有序二分类法,即将基于序数目标变量分解成为多个二元变量,然后由单个模型或多个模型对有序信息预测最终的分类结果,有序二分类方法强调了基于有序选择背后的潜在变量的方法与基于定义良好模式的概率分布的方法。曾庆田等[5]基于频繁模式挖掘的方法,利用K-L散度值来提取最有区分能力的频繁模式,并对将这两种方法进行特征组合,进而来提取序数回归中最有辨识能力的特征,从而提升序数回归模型的训练效果。Yldrm等[6]考虑到数据集中的目标属性值是具有固有顺序的,提出了一种新的集成的有序分类方法(ensemble-based ordinal classifcation,EBOC),该方法结合了装袋算法和提升算法,用于解决交通运输部门中有序分类的问题,并且在准确性方面对所提出的EBOC方法与结合树的分类算法(例如C4.5决策树、随机树和REP树)等传统有序分类器进行比较。结果表明 EBOC方法比传统的序数回归方法能够更充分挖掘排序信息和运用集成策略,从结果上体现出更为准确的分类精度。
(3)阈值模型,因为不同类别之间的距离并没有预先定义,所以阈值模型必须学习不同类间的距离。阈值模型结合数学几何的方法,其中对应的阈值是对预测值进行划分,按照设定好的顺序排列,预测变量的结果是从输入空间投影到与每个类别相对应的一维空间的结果。Wang等[7]提出了非平行支持向量序数回归,该方法学习多个非平行超平面,每个分类等级通过构造定义好的超平面来进行分离,从而该模型可以达到并行学习的能力。Nguyen等[8]提出了一种用于序数分类的距离度量学习方法,将包含排序信息的局部三元约束合并到传统的最大间隔距离度量学习方法。本文所提出的方法是基于第三种类型的序数回归阈值模型,建立面向不确定数据的支持向量序数回归阈值模型。
在过去的几十年里,关于序数回归的文献增长得非常快。虽然序数回归取得了大量的成果,但是,在面向样本不确定性的序数回归工作还是比较少。在现实应用中,由于仪器不精确、采样误差和传输干扰等外界环境的原因,我们所得到的数据可能存在噪声,我们称之为样本数据中的不确定性数据。目前,序数回归工作主要针对分类标签不确定和协同系统的决策不确定性。例如,Dopazo等[9]利用指定区间顺序数据作为捕获不确定和不完整信息的灵活方法好的神经元组排序问题,该模型提出了两阶段的学习方法。第一阶段学习了聚合偏好矩阵,该矩阵可从不确定的和可能相互冲突的信息中收集用户偏好组的一种方法。在第二阶段,通过学习优先级向量,该向量是从基于模糊偏好惯性的性质和图论的聚合偏好矩阵中提取。该方法仅仅是考虑了用户偏好的模糊性,并且放宽了数据的确定性和完整性的假设。Iannario等[10]提出了一种回归模型的综合框架,在序数模型的基础上,结合离散均匀分布和二项式分布 (combination of a discrete uniform and a binomial distribution,CUB),建立了新的有序反映机制,用来考虑决策中的不确定性,该序数回归模型的综合框架可发现数据隐藏的相似性和引入新的数据分布,并且可以观察不同视角的数据,改进统计模型对序数回归机制的解释和预测。Tutz[11]扩展了序数回归模型,优化了传统的CUB模型,他们考虑了偏好部分是由累积或相邻类别决定的分布模型,展现了该模型学习的灵活性,并且引入了赤池信息准则(akaike information criterion,AIC)、贝叶斯信息准则(Bayesian information criterion,BIC)和预后指标对模型中的决策不确定性分量进行分析,可以使得优化的CUB 模型表现出更好的拟合效果和分类性能。总的来说,目前序数回归工作主要针对分类标签不确定和协同系统的决策不确定性,而在样本数据的不确定性方面的研究还比较少。
2 基本概念和符号

本文采用的显式阈值约束的支持向量有序回归模型的目标方程为

(1)
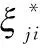
3 基于不确定数据的支持向量序数回归
针对不确定数据的问题,本文提出了基于支持向量序数回归模型来解决有序数据中的不确定数据的方法。由于不确定信息的影响,所有收集的数据x都可能与真实数据存在一定程度上的偏移,本文把这个偏移量表示为Δx。在现实世界中,由于缺乏任何先验知识,我们难以获得的数学分布。根据文献[13]的研究,本文给每个样本的偏移值Δx设置一个边界,如下所示
(2)
其中, Δxji为样本xji由于噪声所产生的偏移,δji为该偏移Δxji模的最大值。
本文把样本偏移量Δx加入训练集样本中,训练集可表示为:T={xji+Δxji}, 其中, Δx⊆Rd。 从训练集中可看出,xji为所收集的训练样本,由于外界噪声的影响,训练样本可能存在一定的不确定信息。 Δxji为样本xji由于噪声所产生的偏移,它是一个未知量。把样本xji转化为xji+Δxji, 可以通过调整Δxji对样本进行校正,令xji+Δxji更加接近真实的样本值。

面向不确定数据的支持向量序数回归模型如下

(3)
在式(3)中,需要优化参数变量ω,bj, Δxji, 式(3)中的第三个约束条件是指所有不确定数据的偏移边界值。
当Δxji固定时,式(3)变成一个关于ω、bj(j=1,…,r) 凸优化问题。当参数ω、bj确定时,式(3)则变成关于Δxji的凸优化问题。优化定理[14]将双凸优化问题通过分解为两个凸优化问题来解决。本文通过以下两个步骤来求解式(3)。
(1)固定Δxji, 计算分类器ω和bj


(4)

(5)
(6)
C+αji-γji=0
(7)
(8)
(9)
将式(6)~式(9)代入到拉格朗日函数(5)中,可得到对偶最优化问题,如式(10)所示

(10)
通过上述方法,可以确定分类器中的ω和bj的值。在下一步中,我们固定ω和bj, 优化Δxji的值。
(2)固定分类器ω和bj, 计算Δxji


(11)
(12)
按照文献[14]的方法,根据原问题(4)中前两个约束,可求解两个不同的Δxji, 本文将这两个不同的Δxji分别设为Δx1和Δx2。ω、bj
(13)
(14)
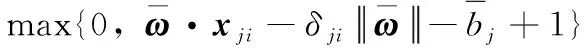
(15)

(16)
k=argmin(k1,k2)
(17)
通过固定ω和bj, 在问题(3)中, Δxji的最优解是
Δxji=Δxk
(18)
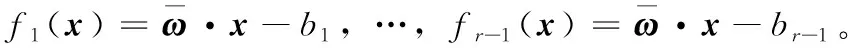
算法1:面向不确定数据的支持向量机序数回归算法

输出:f(x)。
(1) 初始化t=0;
(2)t=t+1;
(3) 如果t=1, 初始化Δxji=0;
(5) 由式 (11) 和式 (12) 来确定Δxji的值;
(6) 根据式 (4) ~ 式 (9) 可计算得到ω、bj;
(7) 令Fval(t) 成为原问题 (3) 的决策函数值;
(8) 令Fmax={Fval(t-1),Fval(t)};
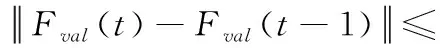
本文是对支持向量有序回归算法的改进,为了提高实际采集数据的准确性,把不确定数据引入到支持向量序数回归中,用来解决现实的有序数据受外界干扰产生的扰动性的问题。整个面向不确定数据的序数回归算法流程如图1所示。
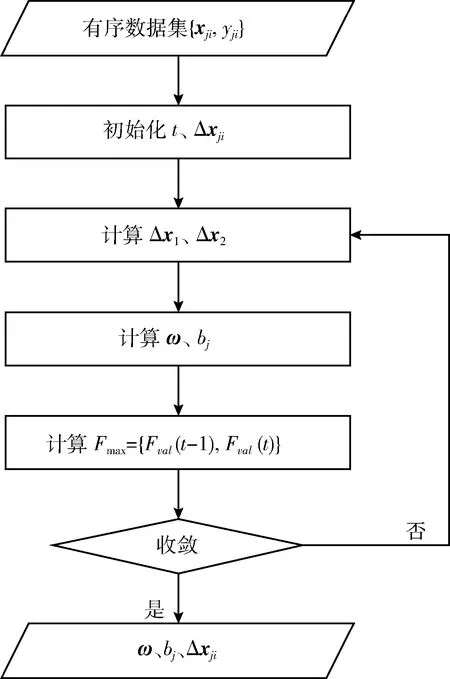
图1 面向不确定数据的序数回归算法流程
4 实验结果与分析
为了研究本文提出的算法的有效性,本文在几个真实的数据集上进行了实验。所有的实验都运行在一台2.2 GHz的处理器和4 GB数字存储器的笔记本电脑上。SVM的算法是基于LibSVM实现的。本次实验的目的是:①评价面向不确定数据的支持向量序数回归模型的有效性;②研究不确定的支持向量序数回归模型对不同比例的数据噪声的敏感性。
本文采用平均0-1误差、平均绝对误差和p值这3项性能指标对实验结果进行分析:
(1)平均0-1误差
(19)

(2)平均绝对误差
(20)

(3)p值
在统计学中,p值是指假设零假设是正确的,获得结果的概率至少与统计假设检验的观察结果一样极端。p值是由匹配好的t检验计算得到。在零假设检验下,当我们将USVOR与其它分类器比较时,这与测试0-1误差分布没有区别。
本文选择了序数回归研究领域中的基准数据集Amazon Sentiment 数据集、BIT-Vehicle 数据集和MSRA-MM数据集来对本文方法进行验证。Amazon Sentiment 数据集源于亚马逊网址Amazon.com,其中包含6类产品的评论:“Cameras”、“Laptops”、“Mobile phones”、“Tablets”、“TVs”和 “Video surveillance”。数据集评论数量分别为 7673 条、2473 条、4471 条、1049 条、2365 条和 2790 条。每条评论都有5个不同顺序的评级标签,分别是:{ 1、2、3、4、5 },较高的评级显示了更好的评论反馈。BIT-Vehicle数据集是由北京智能信息技术实验室构建,其中包括9850张车辆图像用来测试本文的方法。有两个相机在不同的时间和地点捕捉的像素大小分别为1600×1200和1920×1080的图片。本文中所有车辆将分为3个类别:小型(轿车)、中型(SUV,小型客车,小型货车)和大型(客车,卡车)。MSRA-MM 数据集是由微软研究公司收集,其中包含68个查询和19 436张图像。图像检索查询包括天使、鸟类、猫、狗、足球、树等。对于每个输入参数,它与相应查询的相关性被标记为3个级别:非常相关、相关和无关。

为了验证本方法的有效性和优越性,本文方法与5种算法SVOR[12]、USVM[13]、SVM[15]、IUTSVM[16]、SUSVM[17]进行比较。SVOR根据“最大间隔”原则下对k类样本进行排序。然而,SVOR仅仅考虑有序数据,忽略了不确定数据对有序数据的干扰影响。关于SVOR,它可以用来评估USVOR 处理不确定数据的能力;USVM 考虑了输入数据被噪声损坏。原始的 USVM 是基于二分类的方法,我们将 USVM 一对一的形式扩展为一对多的形式,因此USVM也能进行多分类学习; SVM 是从支持向量机扩展为多分类的支持向量机学习算法;IUTSVM是在解决Universum数据的孪生支持向量机(UTSVM)的基础上,引入了一个正则化项解决了优化矩阵中非奇异的问题,本文将其扩展为具有多分类学习的IUTSVM;SUSVM是将原问题中的二次规划问题(QPPs)转化为一对线性规划问题,以此减少此算法的计算时间,本文在此基础上推广具有多分类学习能力的 SUSVM。不同方法的性能比较分别用平均0-1误差和平均绝对误差这两种指标,见表1、表2。

表1 不同方法的平均0-1误差

表1(续)

表2 不同方法的平均绝对误差
不同算法的平均0-1误差、平均绝对误差和p-value见表1、表2。p-value越小,表示算法表现越显著稳定。表1和表2显示了AmazonSentiment数据集上的平均0-1误差和平均绝对误差。以表1中的“Mobile phone”数据集为例,USVOR在平均0-1误差中有0.037至0.116的改进。从表2中可以看出,USVOR在Amazon Sentiment数据集中达到了最佳的分类性能。例如,在“Mobile phone”数据集中,USVOR在平均绝对误差指标上相对于其它对比方法有了0.027至0.514的幅度提升。本文可以观察到,USVOR的平均绝对误差低于SVOR、SVM、IUTSVM和SUSVM。在SVM、IUTSVM和SUSVM中,有序信息被忽略,超平面通常是无序的和相交的。跟SVM、IUTSVM和SUSVM不同的是,USVOR不仅利用平行超平面来划分数据,而且还将有序信息整合到模型中,通过对超平面的约束来划分超平面之间的等级性。本文方法USVOR在平均0-1误差和平均绝对误差上都优于其它5种算法,说明本文方法的有效性和优越性,这是因为USVOR可以在迭代训练阶段通过更新不确定数据的计算来解决基于不确定数据的序数回归学习问题。同时观察到SVOR、USVM、IUTSVM和SUSVM的平均0-1误差和平均绝对误差低于只考虑多分类SVM的方法,因为SVOR方法考虑了数据回归的有序性,但忽略了有序数据中的不确定信息,而USVM考虑了不确定信息的分类但却忽略了数据回归的有序性。IUTSVM和SUSVM对于掺杂了无关数据的有序数据进行分类,仍然存在不足。
本文研究了USVOR、SVOR、USVM、SVM、IUTSVM和SUSVM应对不同程度噪声水平的敏感性。从图2和图3中可看出本文所提取的部分子数据集将噪声百分比从20%增加到100%时的平均0-1误差和平均绝对误差的变化情况。很明显该子数据集随着噪声比的增加,平均0-1误差和平均绝对误差而因此增加。其中,x轴表示添加到训练集中的噪声百分比,其中y轴在图2表示平均0-1误差,y轴在图3中则表示为平均绝对误差。随着噪声百分比的增加,训练数据可能变得难以区分,训练样本受到不确定数据影响产生的矢量偏移程度也会因此而增大。与SVOR、USVM、SVM、IUTSVM和SUSVM相比,当噪声百分比从20%和100%增加时,本文提出的方法USVOR仍然保持最低的平均0-1误差和平均绝对误差的水平,这表明USVOR考虑不确定数据时能够有效抵抗噪声的有效性。

图2 不同数据集在不同程度噪声下的平均0-1误差

图3 不同数据集在不同程度噪声下的平均绝对误差
5 结束语
本文基于不确定数据提出了支持向量序数回归的方法。在支持向量序数回归中引入了不确定数据,解决了有序数据中包含的不确定数据。由于现有的序数回归模型没有考虑有序数据中包含的不确定数据,在处理不确定信息时,模型的抗干扰性差和分类精度并不是很显著。因此,本文将不确定数据考虑在序数回归模型中,有利于提高模型的分类性能。本文采用平均0-1误差和平均绝对误差这两种评价指标。通过对比实验得出的评价指标,本文在平均0-1误差和平均绝对误差性能方面都优于其它3种方法,说明本文方法的有效性和优越性。未来的工作是在多视角数据中研究多视角中的无关信息的序数回归问题。
