非独立同分布下的K-Modes算法

周慧鑫，姜 合，王艳梅

(齐鲁工业大学(山东省科学院) 计算机科学与技术学院，山东 济南 250353)

0 引 言

许多学者根据K-Modes算法[1,2]存在的问题，对算法进行了很多研究和改进。针对初始中心点选择的问题，Liwen Peng[3]提出了一种基于属性权重的选择聚类中心的方法。贾瑞玉等[4]定义了一种新的计算对象密度的方法，通过残差分析得到初始聚类中心。针对相异度量的问题，赵亮等[5]提出了一种基于朴素贝叶斯分类器中间运算结果的距离度量。施振佺等[6]提出了一种基于粗糙集和知识粒度的属性加权算法，加权到相异度的计算中。袁方等[7]提出了一种针对有序分类与无序分类两种属性的距离度量。针对其它方面的问题，黄苑华等[8]提出一种基于结构相似性的K-Modes算法。张春英等[9]提出了一种基于集对信息粒的集对K-Modes聚类算法。叶霞等[10]提出了一种将蚁群聚类算法与K-Modes算法相结合的算法。

到目前为止，相异度量的计算，大多数都考虑的是数据之间是相互独立，没有关系的，然而实际上的数据集中属性之间是存在着一定的耦合关系，即非独立同分布。操龙兵首先提出的非独立同分布思想，随后很多研究学者运用这个思想，用于许多不同的研究方向。操龙兵提出了基于复杂相互作用的耦合性学习。Jian等为无监督学习定义了一个耦合度量相似度(CMS)[11]，它提出了数据对象间的异构耦合关系。Wang等提出了在无监督学习中类别型数据的耦合关系来计算相似性度量的方法并在K-Modes算法中进行了验证。在真实数据中，数据对象的属性之间存在着一定的联系，因此，在非独立同分布的思想下改进K-Modes算法将更加符合实际。

1 K-modes算法

1.1 算法基本概念

在日常的数据中，数据类型主要包括数值型数据和类别型数据。它们之间有本质性的区别，数值型数据是按数字尺度测量的观察值，其结果表现为具体的数值，是属性值的一个数值，属性值之间具有一定的几何特征，可以进行数值运算；而类别型数据是一种非数值型数据，表示的是对象的特征属性，特征的数值既没有数量大小的含义，代表的是属性的各种状态，不能进行数值运算，各种分类内容都属于类别型数据, 如性别分类(男、女)、地区(省、市)、农药毒性(剧毒、高毒、中毒、低毒)等[12]。K-Means算法是适用于连续的数值型数据[13]的聚类算法，以效果更好，思想简单的优点在聚类算法中得到了广泛的应用[14]。现在常用的距离度量方法有很多像欧氏距离、曼哈顿距离、切比雪夫距离、余弦距离，这些方法都是针对对数值很敏感的数值型数据，而类别型数据之间的相似性是对数据特征很敏感，所以传统的K-Means算法中计算数据距离的欧式距离不能计算离散属性之间的距离。K-Modes聚类算法通过对K-Means聚类算法的拓展，使其可应用于类别型属性数据聚类[15]。

K-Modes算法中采用计算数据间相异度量的方法来表示数据间的距离。相异度量越小，则表示距离越小。K-Modes的基本思想是随机分配K个对象作为初始聚类中心，计算隶属度矩阵，将剩余的数据划分到离初始类中心最近的子类中，基于频率更新聚类中心，经过多次迭代，聚类函数收敛，算法划分结束。

1.2 算法描述

输入：数据集，聚类类簇个数K。

输出：聚类后划分好的子类集合。

步骤1 从数据集中随机选择K个对象作为初始类中心，其中K表示聚类过程中簇的个数。

步骤2 采用简单0-1匹配方法计算每个对象与各聚类中心之间的相异度量作为距离度量。某一个对象和另一个对象的相异度量就是它们各个属性不相同的个数，相同记为0，不相同则记为1，最后计算1的总和，这个和就是两个对象间的相异度量。

步骤3 将每个对象分配到相异度度量最小的子类中。

步骤4 使用基于频率的方法更新聚类中心。

步骤5 重复上述的步骤2～步骤4，直到目标函数F收敛，即聚类中心不再发生变化时，算法结束。目标函数见式(1)

(1)

其中，k是聚类类簇的个数，n是数据对象的个数，wli∈{0,1} (1≤l≤k,1≤i≤n,)wli=1表示第i个对象被划分到第l类中，ml为第l个类的聚类中心，xi表示第i个数据对象。

2 NonIID-HDK-Modes算法

2.1 初始聚类中心的选取

传统的K-Modes算法中，对初始聚类中心点是随机选取的，这使得聚类算法的结果会非常依赖初始聚类中心点的选取。随机选取K个中心点，可能会选取到离群点，而且每次中心点选取的不同也会影响到算法的聚类效果。因此，本文提出一种基于层次聚类对数据集进行预聚类的方法，对预聚类划分好的类簇进一步处理后，取得的每个类簇中的聚类中心作为K-Modes的初始聚类中心，改变传统算法随机选取中心点的缺点。

层次聚类的相似性指的是任意一个数据对象ux与所有数据对象之间的距离，它们的距离越小，相似度就越高。层次聚类的思想就是将相似度高的数据对象不断的进行合并，直到合并到设定的K个类簇，结束算法。

基于层次聚类预聚类的初始聚类中心选取方法的具体步骤是：

(1)对数据集的数据进行归一化处理

在数据集中，不同属性指标往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果，为了数据处理方便，对数据进行基于均值和标准差的归一化处理

(2)

其中，μ为所有样本数据集的均值，σ为所有样本数据集的标准差。

(2)对数据集进行层次聚类预聚类

计算类簇之间的距离，常用的方法有：最小连接距离法、最大连接距离法、平均连接距离法。采用适用于类别型数据的平均连接距离法计算距离公式如式(3)所示，将数据集中所有数据都当作是一个独立的类簇，对于给定的聚类簇Ci和Cj，找到距离最小的两个类簇C1和C2

dmax(Ci,Cj)=|mi-mj|

(3)

其中，mi是簇Ci的均值，mj是簇Cj的均值。

合并距离最小的C1和C2为一个类簇，然后不断合并距离最近的聚类簇，并对合并得到的聚类簇距离矩阵进行更新。不断重复上述过程，直至达到K个聚类簇。

(3)分别计算K个类簇中每个对象的局部密度和高密度点距离。

把每个聚类簇中的所有数据对象作为一个子集，分别计算每个子集中每个数据对象的局部密度，局部密度计算公式如式(4)所示

(4)

其中，dij表示任意的数据对象xi和数据对象xj之间的距离，用欧氏距离进行计算，计算公式如式(5)所示

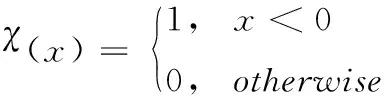
(6)

dc是一个截断距离参数，设置dc为数据量的1%，把每个样本点和所有样本点的距离与先前设定好的截断距离相比较，所有小于截断距离的点的个数就是这个样本点的局部密度大小。

接着，计算高局部密度点距离如式(7)所示

(7)

(4)选取聚类中心

ρi和δi相对较高的数据点标记为簇的中心，所以计算每个子集中ρi和δi的乘积，即γi，取γi的最大值，将每个类簇中的最大值的数据点作为每个类簇中的聚类中心

γi=ρiδi

(8)

将选取出来的所有K个类簇的聚类中心作为K-Modes算法的初始聚类中心。

2.2 相异度量的计算

在传统的K-modes算法中，相异度量的计算都是基于距离的度量方法，是以数据属性之间的存在是独立同分布为前提的，然而现实生活中的数据的属性之间都是非独立同分布的。在Wang的文章里将非独立同分布的思想加入到K-Modes算法的相异度量的计算中与Ahmad等提出的ADD相异度量的计算方法进行了实验比较，发现在数据结构分析和聚类质量方面，提出的方法优于其它类别型数据的相异度量的方法。所以将非独立同分布的思想加入到K-Modes算法的相异度量的计算中是可行的。

在Wang改进的K-Modes的算法中属性之间的耦合相似度的权重参数认为每个属性的重要程度是均等的，不能反映属性间真实的权重参数。互信息反映的是任意两个对象的联合分布相对于假定两个对象是独立情况下的联合分布之间的内在依赖性，度量两个事件集合之间的相关性，属性之间的耦合相似性体现的就是某个属性值与其它属性值的共现依赖关系，所以可以采用计算互信息的方法来计算属性之间的权重关系，在本文中计算属性之间的互信息后对互信息进行标准化，得到属性的权重矩阵，更好反映出每个属性的重要程度以及更加合理改进了计算对象差异度量的方法。

设数据集集合为U={u1,u2,…,um}， 表示一组非空的m个数据对象组成。A={a1,a2,…,an}， 表示每个数据对象包括n个属性，是一组有限的属性。V=∪j=1nvj表示的是属性值集，Vj是属性aj的值的集合。

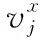
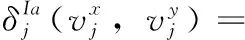
(9)

IaASV反映的是属性的属性值频率之间的关系，频率近似相等的两个属性值具有较大的相似性。

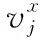
(10)

(11)

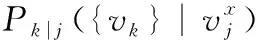
(12)

2)αk是属性ak的权重参数，利用标准化互信息求取权重矩阵对αk赋值，计算公式如式(13)所示

(13)

I(ai,aj) 是指属性ai和aj的互信息。计算公式为式(14)

(14)

其中，p(vi)，p(vj) 分别是属性值vi和vj在数据集U中的概率分布函数。p(vi,vj) 是属性值vi和vj在数据集U中的联合概率分布函数，计算公式如式(15)所示

p(vi,vj)=p(vi)·p(vj)

(15)

H(ai) 表示的是属性ai的信息熵，计算公式为

(16)

(3)对象的耦合属性不相似性(CADO)为

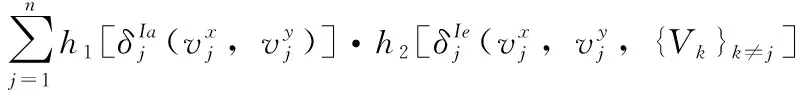
(17)

令h1=1/t-1，h2=1-t，h1(t)，h2(t)， 都是关于t的递减函数，满足相似性和不相似性的互补性。

计算相异度量的步骤为：

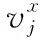
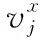
步骤3 求取权重矩阵对对αk赋值

步骤4 计算任意两个对象ux和uy之间的对象耦合属性不相似性CADO，得到数据对象间的距离矩阵作为数据对象之间的相异度量。

本文选取Breast-cancer数据集中的一个片段为例计算数据片段的相异度量矩阵，6个对象具有8个属性，分为两类，具体信息见表1。

表1 Breast-cancer数据片段

将表1 按照相异度量的计算方法，计算出表1的相异度量见表2。

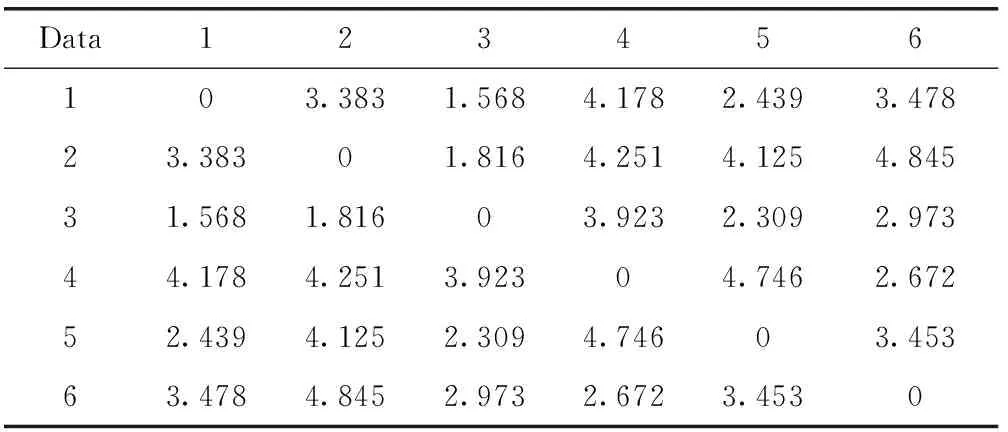
表2 数据片段的相异度量

2.3 算法描述

输入：数据集，聚类类簇个数K。

输出：聚类后划分好的子类集合。

步骤1 按照2.1中的思想选取K个聚类中心。

步骤2 根据2.2中方法计算数据集中任一数据对象ux与选取的聚类中心之间的相异度量。

步骤3 将每个对象分配到与聚类中心相异度量最小的子类中。

步骤4 分配结束后，通过基于频率的方法来重新确定聚类中心。

步骤5 重复上述的步骤2～步骤4，直到所有数据对象所属的聚类中心不再变化时，算法结束。

以上是对K-Modes算法初始聚类中心的选择和相异度量进行了改进，考虑到数据之间的属性相似性，更好地处理了类内间相似性的问题，解决了传统K-Modes算法随机选取中心点和计算相异度量时忽略了类内相似性的问题，更好提高了算法的聚类效果。

3 实验结果及分析

本文实验在UCI数据集分别是Zoo数据集、Breast-cancer数据集及Soybean-small数据集这3个数据集上进行实验验证。

实验环境：MATLAB R2019b，Intel(R) Core(TM) i7-6700CPU、3.40 GHz、8.0 GB，Microsoft Windows 7。

3.1 实验描述

本文改进了传统随机选取中心点的缺点，并改进非独立同分布的公式引入到计算K-Modes算法的相异度量中，主要目的是提升K-Modes算法的聚类精度，避免选取初始聚类中心的时候选到离群点或者同一类别的情况，同时使属性的权重参数更加合理化，更加准确的将属性内耦合和属性之间的耦合的相似性加入到计算数据对象的相异度量中。

本文分别在Zoo数据集、Breast-cancer数据集和Soybean-small数据集上进行了实验验证。将数据集在相同的环境中分别在传统的K-Modes算法、Wang改进的K-Modes算法(简称Wang)、文献[16]和NonIID-HDK-Modes的算法程序中运行20次，分别记录下每个算法聚类的正确率。

3.2 实验结果

3.2.1 数据集描述

3个数据集的描述见表3。

表3 数据集信息

3.2.2 实验对比结果

下面分别从分类正确率(AC)、类精度(PR)、召回率(RE)这3个方面来分析算法的聚类质量，AC、PR、RE的定义分别如下

其中，U表示的是数据集中的对象的数量，K表示的是聚类类簇的个数，xi表示可以正确分到第i类的对象数量，yi表示错误分到第i类的对象数量，zi表示应分到却没分到第i类的对象数量。

在Zoo数据集、Breast-cancer数据集和Soybean-small数据集3个数据集中，验证传统的K-Modes算法、Wang、文献[16]的算法和NonIID-HDK-Modes算法。4个算法在相同的环境中运行20次取平均值，具体聚类算法性能比较见表4～表6和图1。

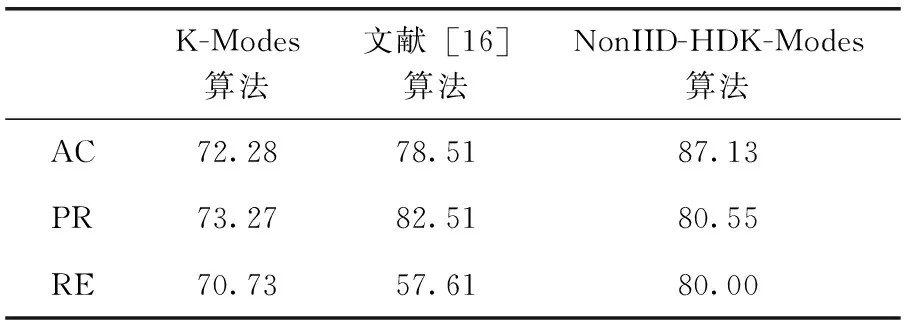
表4 在Zoo数据集下性能比较/%

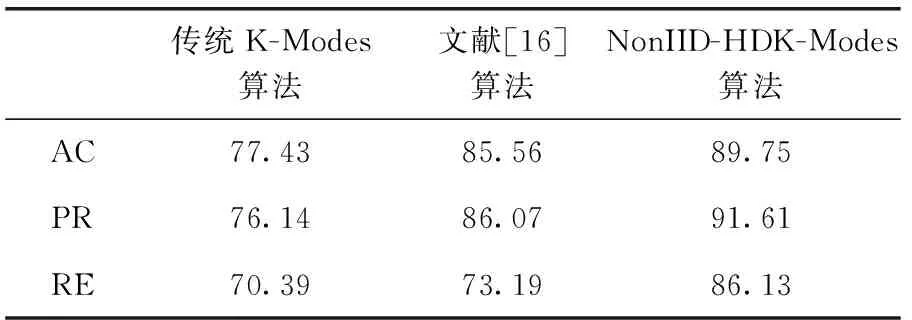
表5 在Breast-cancer数据集下性能比较/%

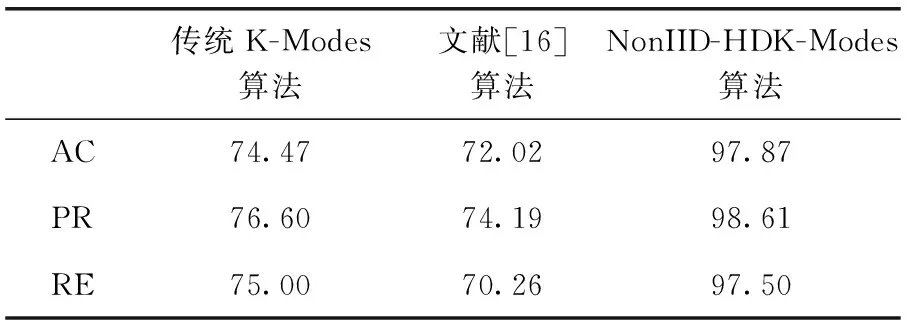
表6 在Soybean-small数据集下性能比较/%

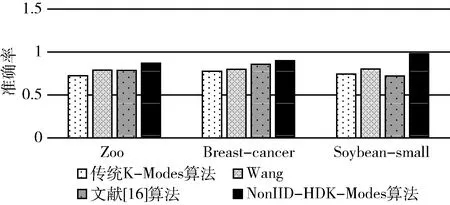
图1 4种算法的准确率

通过分析图1，可以发现在非独立同分布思想下，NonIID-HDK-Modes算法比Wang算法中改进K-Modes算法相异度量的聚类效果更好，准确率更高。

通过分析表4～表6，可以看到在数据集Zoo、Breast-cancer和Soybean-small上，经过修改非独立同分布思想下计算耦合相似性的权重参数和初始聚类中心点选取方法的K-Modes算法与独立同分布条件下的K-Modes算法的对比，NonIID-HDK-Modes算法获取了较好的聚类效果，聚类结果优于文献[16]，验证NonIID-HDK-Modes算法是有效的。

3.3 实验分析

根据实验得到的结果，可以看到Wang的算法在非独立同分布的思想下把属性内和属性之间的相似性一起加入到计算相异度量时，聚类效果会相比传统的K-Modes算法有一定的提高。因此，把非独立同分布的思想引入到K-Modes算法中是可以提高算法的聚类效果的，是可行的。

通过图1我们可以看到，在非独立同分布的条件下，在相同的运行环境下3个数据集中NonIID-HDK-Modes算法与Wang对K-Modes算法的改进相比，可以更好提高聚类算法的准确率，说明改进耦合权重和初始聚类中心的选取方法是有效的。

由实验结果可以看到，基于非独立同分布的思想的NonIID-HDK-Modes算法在Zoo数据集中，相比较文献[16]的方法聚类准确度提高了8.62%；在Breast-cancer数据集中，相比较文献[16]的方法聚类准确度提高了4.19%；在Soybean-small数据集中，相比较文献[16]的方法聚类准确度提高25.85%。在Zoo数据集和Soybean-small数据集与Breast-cancer数据集的准确率提高的较多，两个数据集中的数据较少，算法准确率的提高较为明显，对于数据集中数据较多的情况，算法的准确率效果较为不明显。因此，NonIID-HDK-Modes算法可以更好提高较小数据集的聚类准确率，对于提高较大数据集的准确率存在不足。

通过比较聚类的纯度大小，判断算法聚类效果的好坏，当聚类的纯度越接近1，说明算法聚类的效果越好。传统K-Modes算法、文献[16]和NonIID-HDK-Modes算法在3个数据集上的纯度见表7，在Zoo和Soybean-small两个数据集上，NonIID-HDK-Modes算法表现较好，聚类的效果更好。在Breast-cancer数据集上，文献[16]的聚类效果更好，说明改进的算法在整体上还是能够有效提高算法的聚类纯度，提高聚类的效果，这得益于非独立同分布的思想。

表7 3种算法的纯度比较

4 结束语

在本文中针对K-Modes算法随机选取初始聚类中心的缺点，首先对数据集通过层次聚类预聚类对数据集进行类别划分，然后再分别计算每个类别中所有对象的局部密度和高密度点距离，选择两个距离乘积的最大值作为每个类别的一个聚类中心，逐一选取每个类别的聚类中心，并将所有类别的聚类中心作为算法的初始聚类中心。同时传统的K-Modes算法计算相异度量时，忽略了数据对象之间的联系，在本文中根据非独立同分布的思想计算相异度量，并且在非独立同分布的基础上继续改进计算属性耦合相似性权重参数的方法，计算两列间的标准化互信息作为权重矩阵。实验结果表明，本文在非独立同分布的思想下提出的NonIID-HDK-Modes算法具有较高的准确率，可以提高K-Modes算法聚类的效果，更加符合现实中数据的实际情况。