棉纺质量影响因素关联性分析
2023-01-31张家宝邵景峰
张家宝 徐 洋 邵景峰
(西安工程大学,陕西西安,710048)
棉纺质量预测是棉纺学术界长期探讨但又未能彻底解决的热点问题,这其中的最大难点在于影响棉纺质量的因素众多且相互交织,导致其中的关键因素难以识别。揭示棉纺质量特征值的波动机理、明晰各类影响因素与棉纺质量特征值之间关系是解决该问题的重要举措。
学者们对棉纺质量预测的研究始于20世纪90年代初[1],其研究焦点在于相关优化算法在棉纺质量预测方面的应用。比如ADMUTHE L S等[2]利用减聚类、模糊神经网络和遗传算法,提出了一种混合纺纱质量预测模型,并将其应用于纺纱过程的模拟和优化;ZUREK W等[3]根据单纤维应力-应变曲线的分析和纤维性能建立数学模型,预测纱线的强力和断裂伸长率;PULIDO M等[4]根据纤维的3个重要特性(长度、细度和强力)之间的线性关系,研究了纤维长度与棉纺质量之间的线性关系。后来,随着理论研究的不断深入,其研究焦点在于通过数据、优化算法对质量预测模型进行训练方面。比如AKHTAR K S等[5]针对BP训练算法收敛于局部极小的问题,将差分进化和LMBP算法结合形成一种混合算法(Hybrid Algorithm),提出了一种基于混合算法的纺纱质量预测模型;MOZAFARY V等[6]借助纱线数据,提出了一种将聚类和人工神经网络相结合的挖掘算法,并将其用于纺纱质量预测;PEYRAVI A等[7]提出了一种基于稳健回归和附加平方和的纱线质量预测方法。
在我国,众多学者们从不同视角探讨了这一问题,早期的研究焦点主要集中在基于支持向量机的纺纱质量预测模型方面。比如YANG J G等[8]研究基于支持向量机的纱线质量预测模型,结果表明该模型在小样本和噪声数据环境下仍能保持一定的预测精度;李蓓智等[9]针对支持向量机在参数选择方面的费时问题,充分利用遗传算法的全局搜索能力,提出了一种基于遗传算法的支持向量机参数选取方法。近年来,随着智能技术在棉纺过程的应用,学者们的研究焦点集中在质量预测模型的训练方面,比如LIANG X等[10]提出了一种基于免疫神经网络的双向智能优化模型,将其用于解决纤维生产过程中的过程优化和品种开发,实现了工艺配置和产品性能的双向建模,其计算性能优于神经网络优化模型;HAN H G等[11]提出了一种基于改进LM学习算法的自组织模糊神经网络预测模型,结果表明该模型的网络结构紧凑且预测精度有了显著提高;许少华等[12]提出一种基于混沌遗传与带有动态惯性因子的粒子群算法相结合的神经网络算法,解决了神经网络模型在训练过程中训练速度慢的问题。
通过文献回顾发现,国内外学者对纺纱质量预测的研究主要围绕纤维属性、纺纱质量及工艺参数之间的依赖关系进行建模或算法设计,但还缺乏纤维属性与纺纱质量之间非线性关系的探讨,以及影响因素与纺纱质量之间关系的研究。
1 问题定义
棉纺过程流程长、工序多,是一个典型的复杂工业系统[13]。在这个工业系统中,每天产生的数据除正常的生产设备、生产过程和运行管理数据外,还包括传统的控制回路、文本类型的订单、纱疵图像等非结构化数据,并随着应用精度的提高呈几何级递增,形成了典型的“海量纺纱数据”。
在海量数据环境下,影响棉纺质量的因素众多(如原料、人、设备等)且相互交织,致使棉纺过程的质量难以实时预测。为此,根据人机系统工程学理论,将影响棉纺质量波动的各类因素k分为纤维属性、系统(由于纺纱设备生产商预先给纺纱设备安装了生产控制系统,在整个纺纱过程中,企业判断纺纱产量、质量的优劣均以此系统数据为基准,为此该系统的性能指标、控制基准、计数标准等对棉纺质量数据精度直接产生影响,本文将这种影响定义为系统)、人为、设备、工艺方法、车间温湿度6大类,并分别定义为矢量Z,即Z=(Z1,Z2,…,Z6)T。这样,在棉纺过程中,将各质量输出特征值定义为Yj(j=1,2,…,q)。其中,j表示质量特征值数量;q表示质量特征值总数,且j≤q。同时,第k个因素Zk(k=1,2,…,6)对质量特征值Yj的影响,可以定义成如式(1)所示的映射函数关系[14]。
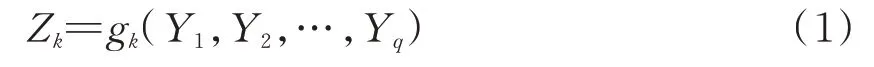
式中:gk为映射函数。
2 棉纺质量损失函数设计与计算
2.1 基于多重相关特征的质量损失公差
为了进一步表达影响因素与多个质量特征值之间的相关关系,利用Taylor公式将式(1)展开,并从中略去二阶以上的高次项,使其形成式(2),并将式(2)进行转化使其形成式(3)。
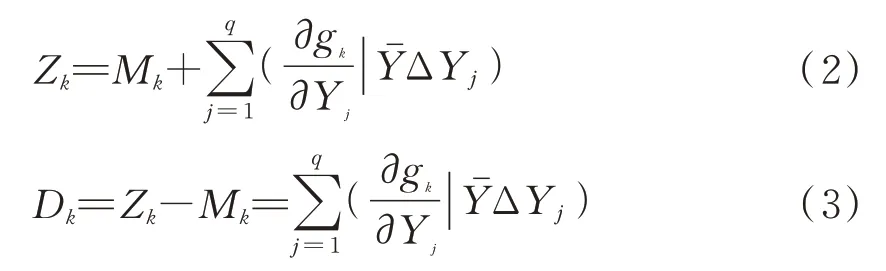
式中:ΔYj表示质量特征值Yj与其质量特征值平均值之间的偏差,即ΔYj=Yj-,Mk=gk();Dk表示质量特征值。
根据贝叶斯统计理论,假设所有的棉纺质量特征值的波动规律遵循正态分布,则质量特征值Dk遵循正态分布[15],由 此Dk的 方差可表示为式(4)。其中,k=1,2,…,r,且r∈N。
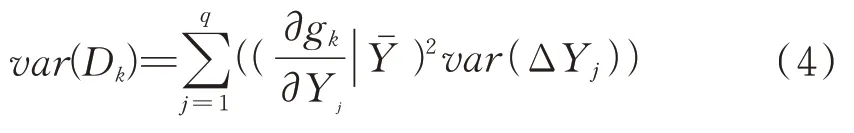
如果棉纺质量特征值之间有共同的特征,并且它们是相关的,那么第k和第k-1个特征值的协方差可表示为式(5)。其中,k=1,2,…,r。
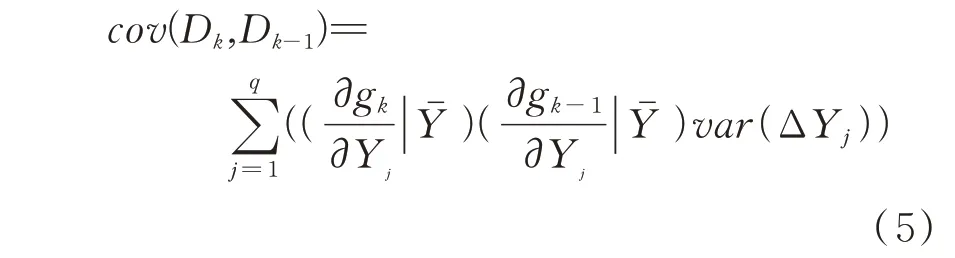
2.2 基于工艺参数公差的质量损失函数设计
根据棉纺工艺理论,棉纺质量形成过程中的纤维属性、工艺参数与纺纱质量之间相关关系,可设计成如图1所示的相关关系。
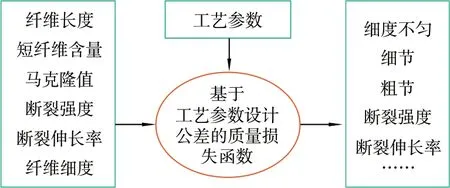
图1 工艺参数与棉纺质量相关关系
根据图1,将棉纤维属性值(纤维长度、短纤维含量、马克隆值等)与工艺参数(纱线号数、捻度、钢丝圈直径等)进行组合,将其作为一个工艺参数组合函数Xji(i,j=1,2,…,p),其中p表示生产工序总数。在此基础上,将条干CV、细节、粗节、断裂强度、断裂伸长率作为棉纺质量特征值Yj。这样,Yj与Xji之间可构成一种函数关系,如式(6)所示。
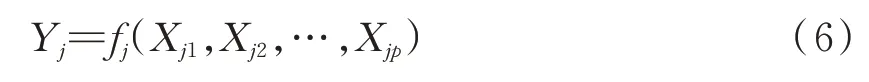
式中:Xji表示质量特征值Yj的第i步工艺参数组合;fj为映射函数。
同时,假设工艺参数组合函数Xji遵循正态分布,则Yj与Xji之间存在如式(7)所示的关系式。
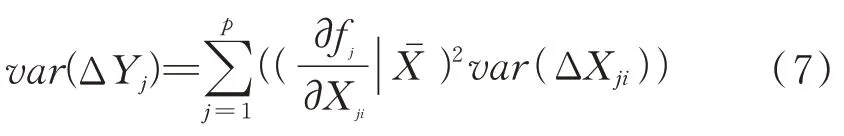
式中:ΔXji表示工艺参数组合Xji与其平均值之间的偏差,即ΔXji=Xji-。
将式(7)代入式(4)和式(5),则可得如式(8)和式(9)所示的关系式。
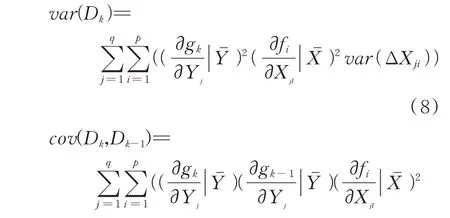

由此,在棉纺质量形成过程中,可以设定每个棉纺质量特征值及公差遵循正态分布,并假定其相对于公差中点呈对称的正态分布。这样,若棉纺质量特征值的波动范围为±3δ(δ为正态分布的标准偏差),则质量波动范围为±0.027%[16],这个结果在棉纺质量管理过程中是可以接受的。
3 基于因素识别的棉纺质量预测方法
灰色关联分析方法作为灰色系统理论中的一种分析方法,在分析和确定系统诸因素之间的影响程度方面具有优势,这为探究影响因素与棉纺质量特征值之间的相关关系提供了理论依据。
为此,将整个棉纺质量形成过程视为一个灰色系统。在这个系统中,借助灰色关联分析方法中的参考序列与比较序列,分析各类影响因素与棉纺质量特征值之间的关系。具体过程如下。
(1)确定参考序列和比较序列。首先,以棉纺过程中最关键的细纱工序为例,以典型的F1518型细纱机为研究对象,按照细纱机罗拉转速脉冲信号的产生周期1个/s,将其按照脉冲波峰的形成过程被等分成4个数据采集点,这样每个数据采集点间隔为0.25 s。然后,按照采集点间隔,将整个棉纺过程数据采集点上对应的棉纺质量特征值波动幅度定义为{X0j},其中j=1,2,…,N(N为数据采集点数),并将其作为参考序列,同时将各类影响因素构成的时间序列定义为{Xij},并将其作为比较序列,其中i=1,2,…,M;M为影响因素总数。在此基础上,利用参考序列与比较序列的相关关系,以参考序列为行、比较序列为列构造影响棉纺质量形成过程的矩阵X,如式(10)所示。
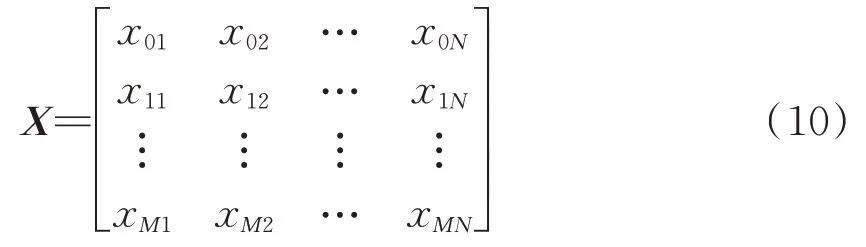
式中:x0j是参考序列,表示棉纺质量特征值的波动幅度;xij是比较序列,表示影响棉纺质量的因素序列,且i=1,2,…,M;j=1,2,…,N。
(2)数据变换。由于各序列数据的量纲和绝对值的大小之间存在差异性,因此还需对序列的原始数据进行变换,将其转化为数量级大体相近的无量纲数据。就数据的变换而言,目前常用的方法主要有初值化、均值化以及区间值化。
由于棉纺过程中的生产设备、生产过程和运行管理数据,以及控制回路数据等,其采集和处理方式均以区间数据为主,因此在数据变换时利用区间值化进行变换,具体过程如式(11)所示。
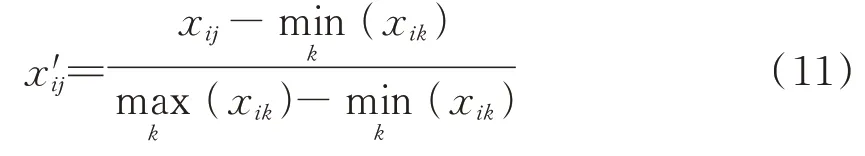
式中:i=0,1,…,M;j,k=1,2,…,N。
(3)求X′中比较序列与参考序列之间的求差序列Δij。在式(11)的基础上,由Xij形成新矩阵,由此得到的求差序列如式(12)所示。

(4)求两极最小差和最大差。根据灰色关联分析方法,计算所得的两极最小差和最大差如式(13)所示。
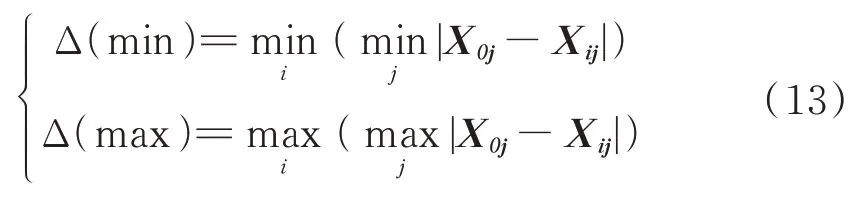
(5)计算关联系数Lij。关联系数的计算过程如式(14)所示。
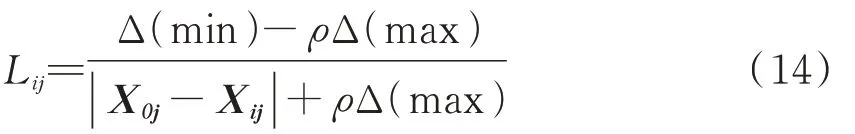
式中:ρ为分辨系数且其值范围为(0,1),表示影响因素对棉纺质量的关联程度。
(6)计算关联度γi。在式(14)的基础上,将影响棉纺质量的各类因素的关联系数累加并求平均数,即为各影响因素的关联度,具体的计算过程如式(15)所示。
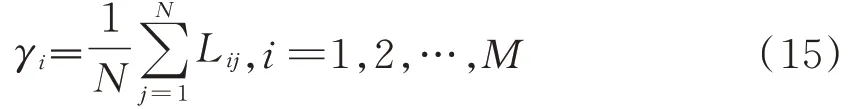
(7)关联度分析。在式(15)的基础上,对计算所得的关联度进行排序,其中关联度最大的序列所对应的影响因素,即为影响棉纺质量特征值波动的关键因素。
4 数据选择与应用验证
4.1 数据选取
以常用的JC 9.7 tex品种为例,从JC 9.7 tex管纱生产数据中获取棉纺质量特征值(条干CV、细节、粗节、断裂强度、断裂伸长率),并用区间值化进行数据变换,具体选取原则:在数据采集过程中将没有产生异常的纺纱质量特征值去除,这样对每个数据采集点进行3次试验,获得用来分析质量损失或质量特征值波动的数据约1 000个。JC 9.7 tex部分管纱质量数据如表1所示。

表1 JC 9.7 tex部分管纱质量数据表
4.2 试验验证
根据表1中的数据可知,本试验棉纺质量特征值的波动偏差是服从正态分布的。
结合表1中的数据,根据第1节中的问题定义,将影响棉纺质量的因素分为纤维属性、系统(各类标准)、人为、设备、工艺方法、车间温湿度6大类,在此基础上仿真6类影响因素即Z=(Z1,Z2,…,Z6)T分别对JC 9.7 tex管纱质量特征值的影响占比,以形成影响因素与质量特征值直接的关联系数,其结果如图2所示。
图2结果表明,各类影响因素对管纱质量的影响程度均不相同。影响质量特征值波动最大的是纤维属性,而车间温湿度、设备及工艺方法对棉纺质量特征值的占比基本接近。相反,影响程度最小的是人为因素。

图2 6大影响因素对管纱质量特征值的影响占比
在此基础上,以参考序列为行、比较序列为列构造棉纺质量特征过程矩阵Xij。
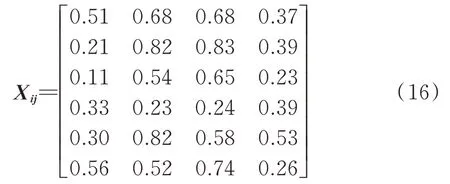
利用公式(11)对矩阵Xij中的数据进行采取区间值化处理,得到转化后的矩阵,然 后利用公式(12)、公式(13)可得出矩阵的两极最小差和最大差,即Δ(min)=0;Δ(max)=1。同时,根据公式(14)和公式(15),得出各影响因素即Z=(Z1,Z2,…,Z6)T与棉纺质量特征值的关联度γi,并按关联度γi进行排序,其结果如图3所示。
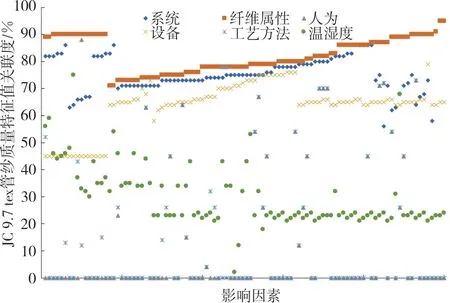
图3 影响因素与棉纺质量特征值的关联度
根据人机系统工程学理论,在选取的3组试验数据中,按照关联度从大到小的顺序进行排序,依次为纤维属性、系统、设备、车间温湿度、工艺方法、人为因素,这一结果说明前3个因素与棉纺质量特征值波动的关联度较大,是影响质量波动的主要因素。同时,根据图3可知,纤维属性与系统之间呈现基本正相关关系,并且纤维属性、系统和设备因素的影响行为都较为显著,进一步确定纤维属性、系统和设备是影响纺纱质量特征值波动的关键因素。同时,在试验结果中,人为、工艺方法与纤维属性、系统、设备5个因素间无关联,说明人为、工艺方法两个因素对质量特征值波动的影响较小,属于次要因素。而且,人为因素在试验过程中与棉纺质量特征值的关联度最小,说明其对棉纺质量特征值几乎不产生影响,并与其他5个因素不相关。
5 结论
首先,基于棉纺过程数据(如生产设备、生产过程和运行管理等数据)对棉纺质量的损失原因进行了分析;在此基础上,设计了基于多层相关特征值的质量损失公差以及基于公差的质量损失函数,对棉纺质量特征值之间的多重相关性进行了表征;根据人机系统工程学理论,分析了影响棉纺质量特征值的各类因素,并将其分为纤维属性、系统、人为、设备、工艺方法、车间温湿度6大类,进一步探讨了各类因素之间的相关关系。其次,将整个棉纺质量形成过程视为一个灰色系统,并借助灰色关联分析方法中的参考序列与比较序列,分析了各类影响因素与棉纺质量特征值之间的关系,并仿真了两者之间的关联关系和关联度,进而通过关联度的排序可知影响棉纺质量特征值的关键因素,并通过试验进行了验证。试验结果表明:纤维属性、系统、设备3个因素与棉纺质量特征值波动的关联度最大,是影响质量波动的主要因素;人为因素几乎对棉纺质量不产生影响,这一结论为棉纺企业的质量预测提供了理论依据。
