基于格子Boltzmann方法的起落架阻尼油孔参数研究

甘盛勇， 魏小辉 ， 房兴波

(1.南京航空航天大学 航空学院，南京 210016； 2.南京航空航天大学 机械结构力学及控制国家重点实验室, 南京 210016； 3.南京航空航天大学 飞行器先进设计技术国防重点学科实验室, 南京 210016)

油气式缓冲器有着缓冲效率高、结构稳定性好的优点，被广泛应用在各种型式的飞机起落架中。油孔阻尼是缓冲器吸收着陆冲击能量和减小地面滑跑垂向扰动的关键部件，在缓冲过程中将飞机降落的机械能转化为内能，油孔阻尼产生的载荷则直接影响飞机垂向过载。为了满足机载设备工作环境和乘客舒适性的设计要求，需要对油孔阻尼性能进行准确分析和设计。

目前起落架缓冲动力学分析基于二自由度质量模型，缓冲器运动特性通过两质量运动差异得出。缓冲器运动特性、油孔结构和初始充填参数共同决定缓冲载荷的大小。其中缓冲器压缩速度特性和油孔截面积不仅直接被用于对阻尼力的计算公式中，还对流动缩流系数的大小产生影响，进一步影响阻尼力变化趋势。目前对于缩流系数的确定方法可以分为工程估算法、经验公式法和计算流体动力学(computational fluid dynamics ,CFD)分析法。工程估算法计算油孔阻尼力时，在整个缓冲过程中将缩流系数确定为常数[1-2]，对于直角入口圆柱孔建议取值区间为0.632～0.707[3]。经验公式法是对特定结构油孔在有限参数区间内进行试验，根据试验结果，得到缩流系数关于部分关键参数的计算公式，利用该公式计算试验参数区间内的缩流系数[4-6]。CFD分析法基于数值计算方法，利用特定参数下的试验数据验证计算模型结果的准确性后，对一般结构参数的油孔进行流动特性分析[7-8]。工程估算法在设计完成后利用起落架落震试验结果对流孔结构进行修正，需要较多的时间成本和经济成本。经验公式法得到的公式只适用于试验参数区间内，其不可拓展性限制了该方法的应用范围。CFD分析法具备时间和经济成本上的优势，在验证计算准确性的前提下，对于阻尼油孔分析具有一定有效性。

格子Boltzmann方法(lattice Boltzmann method,LBM)是一种基于粒子的CFD方法，通过模拟粒子的传播和碰撞过程来模拟流体的宏观运动，在处理复杂边界、介观-微观相互作用和算法并行化方面具备优势[9]，被广泛应用在医学[10]、化学[11]和工程[12]中。基于LBM的大涡模拟(large eddy simulation,LES)分析高雷诺数流动的精度与传统的有限体积法(finite volume method，FVM)的LES相当，且LBM的计算效率更高[13]。浸入边界-LBM在计算流固耦合问题的有效性[14]可以应对更为复杂及可变的油孔结构阻尼特性分析，例如对动结构边界的处理方法[15]。

现有文献中关于缓冲器油孔阻尼的CFD分析更多关注油孔几何参数在起落架落震性能中的影响[16-18]，以及油孔流动静压力和流速分布情况[19]。油孔几何参数对落震性能的影响规律会随着起落架其他参数变动而失去代表性，油孔流动静压力和流速分布也不能直接指导油孔结构设计。为了得到直角入口圆柱孔缩流系数的一般计算公式，基于格子Boltzmann方法对油孔在不同几何参数和工作环境参数下的阻尼性能进行仿真计算，在单参数分析结果的基础上，利用多元线性回归方法得到缩流系数在设计参数区间内的拟合方程。本研究对不同参数的油气式起落架定截面油孔阻尼设计具有一定指导意义。

1 油孔结构及流动特性分析

1.1 油孔结构

油气式缓冲器内部被油孔分割成两个腔体，其中一侧腔体充填满油液，称为油腔，油液为不可压缩流体，另一侧腔体充填部分液体和部分气体，称为气腔。飞机降落或滑跑过程中，缓冲器被压缩后，油腔内部静压力首先增大，油液在静压力作用下，通过油孔流入气腔减小气体体积，气体压力增加为起落架提供气体弹簧载荷。缓冲器内部结构如图1所示。

图1 缓冲器及流孔流动示意图Fig.1 Diagram of shock absorber and oil hole flow

1.2 油孔理论特性分析

油液流动截面从压油面积突然减小至流孔面积，流动截面收缩产生的局部阻力是吸能的主要因素。油液流动截面收缩后，在油孔入口后一定距离处产生一个射流直径最小的收缩截面c-c，收缩截面位置根据油孔长度可能分布在流孔内部或者流孔出口后端，收缩截面位置对油孔流动特性有一定影响。因为来流速度远小于流孔内部截面平均流速，忽略来流速度的动能，在不考虑油孔产生的局部阻力和沿程阻力条件下，根据伯努利方程，油孔出口理论平均流速应该为

(1)

式中：vth为油孔出口理论平均流速；ΔP为油孔两侧静压力差；ρ为油液密度。根据缩流系数的物理意义，即油孔流动实际质量流量和理论质量流量的比值，则缩流系数的计算形式可以表述为

(2)

(3)

2 格子Boltzmann方法及仿真设置

2.1 格子Boltzmann方法

通过对Boltzmann-BGK方程在速度、时间和空间上的离散得到格子Boltzmann-BGK方程[20]为

(4)

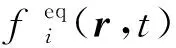
(5)

式中：wi为权系数；u为流体宏观平均速度；cs为格子特征声速。平衡态分布函数的计算取决于流体局部密度ρ和速度u，这两个量可以通过局部粒子分布函数统计值计算得来，而流体宏观速度则可以通过动量密度和质量密度的比值得到，具体表达形式为

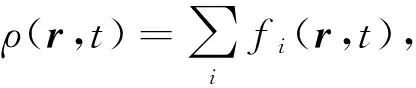
(6)

格子Boltzmann-BGK方程描述粒子运动可以分为两个过程：碰撞项和传播项，表述形式分别为

(7)

图2 格子Boltzmann方法计算过程Fig.2 Lattice Boltzmann method calculation process

2.2 仿真设置

缓冲器定截面油孔为直角入口圆柱孔，影响流孔阻尼性能的主要参数有：油孔长度和直径、流孔出口处静压力。采用控制变量法，在其他参数保持不变的情况下，改变研究变量的大小，设置仿真工况进行计算，各参数在仿真中的基础值如表1所示。

表1 油孔参数基础值Tab.1 Oil hole parameters base value

仿真中边界条件的设定尽量模拟真实的缓冲过程。边界条件设置如表2所示。

表2 仿真边界条件设置Tab.2 Simulation boundary condition setting

根据在参数为基础值工况下进行的计算区域格子尺寸收敛性分析结果，将油孔处格子大小设置为0.18 mm，格子尺寸沿远离油孔方向依次加倍，共四个尺寸层级，格子设置如图3所示。流体介质为15号航空液压油，其在温度为40 ℃时的密度为837 kg/m3，运动黏度为13.85 mm2/s。

图3 多层级流体格子设置Fig.3 Multi-level fluid lattice setup

3 计算结果与分析

3.1 模型验证

利用Cheng等[21]总结的缩流系数经验公式、Jiang等发表的直角圆柱孔流动试验数据和基于雷诺平均方程(Reynolds-averaged navier-stokes，RANS)的有限体积法数值结果来分析LBM计算模型的准确性。模型中流孔几何参数、边界条件和流体属性与Jiang等研究中试验参数设置保持一致。图4中对比了试验数据、RANS数值结果、经验公式和格子Boltzmann方法计算模型结果中缩流系数随静压力差变化规律。

图4 缩流系数随静压力差变化曲线Fig.4 Variation curve of discharge coefficient with static pressure

根据图4可得，缩流系数在压差计算区间内呈逐渐增大规律，增大速度逐渐放缓。格子Boltzmann方法计算结果与经验公式结果的相对误差较小，最大误差为1.51%，与试验结果的相对误差较大，最大误差为5.48%。RANS数值结果与试验结果的最大相对误差为6.56%。通过四组缩流系数的对比，验证了格子Boltzmann方法在分析直角圆柱孔流动特性中的准确性，可以用于对起落架油孔阻尼性能分析中。

3.2 流孔长度

通过对各长度流孔的流动特性计算，得出阻尼力和缩流系数变化趋势。考虑一般流孔厚度，分别选取长度为5 mm，10 mm，20 mm，30 mm和40 mm的流孔进行计算，其余参数设定为表 1中的基础值。得到阻尼力与压缩速度曲线和缩流系数与压缩速度曲线如图5所示。

图5 各流孔长度阻尼性能随压缩速度变化曲线Fig.5 Variation curve of damping performance with compression velocity for each length of oil hole

从图5(a)可以看出，流孔长度从5～30 mm变化时，阻尼力依次减小，流孔长度从30～40 mm变化时，阻尼力增大。当流孔长度为5 mm时，流孔长径比为1.3，属于薄壁孔的范畴，流动经收缩后扩散没有附壁，流动特性只与压力差有关。而随着流孔长度的增加，流动收缩后扩散开始附壁，收缩界面处流速最大，静压力则最小，形成的负压空间有助于液体通过流孔，所以阻尼力会依次减小。流动从收缩截面扩散后附壁，沿程阻力增加，又增大阻尼力，解释了流孔长度为40 mm时阻尼力略有增大的情况。图5(b)中缩流系数在压缩速度为0.1～1.5 m/s时，随着压缩速度的增大而增加，压缩速度在1.5～2.0 m/s时，缩流系数随着压缩速度的增加而减小，缩流系数随流孔长度增加呈先增大后减小趋势，内在原因和阻尼力变化的因素一样。

图6为压缩速度为2.0 m/s时的各流孔长度下水平流速分布情况，因为流动质量流量一致，所以各长度流速大小基本一致。从图6(a)中可以看出，流孔长度为5 mm时，液体收缩截面位于流孔内部，但液体收缩后扩散没有附壁，总体依然呈薄壁孔流动特性。图6(b)流孔长度增加到10 mm，流动扩散后已经能够附壁，当流孔长度继续增大，流动附壁长度加长，增加了沿程阻力，并且形成的收缩截面直径变小，因此两侧形成的回流空间也更大。在图6(d)中能够观察到明显的液体收缩和扩散的流线变化，而在图6(a)中流动收缩后几乎沿水平方向流动，没有发生明显扩散。

图6 各流孔长度液体水平流速分布Fig.6 Horizontal flow velocity distribution for each length of oil hole

图7对比了2 m/s压缩速度下流动附壁前后流孔内部静压力分布变化。图7(a)中是流孔长度为5 mm时的静压力分布，由于收缩截面在流孔内部，流孔内形成了负压空间，集中在流孔入口处两侧区域。图7(b)是流孔长度为10 mm时的静压力分布，此结构下流动已经附壁，形成的负压空间在流孔入口处的连续区域内。因此流动附壁前后流孔内部都出现了一定区域的负压空间，这是收缩截面处流速最大导致的，然而流动附壁后形成的负压区域分布在流孔入口后的连续截面上，形成的区域比附壁前更大。较大和较连续的负压区域加强了液体的通过能力，进一步验证了流孔长度对缩流系数的影响趋势。

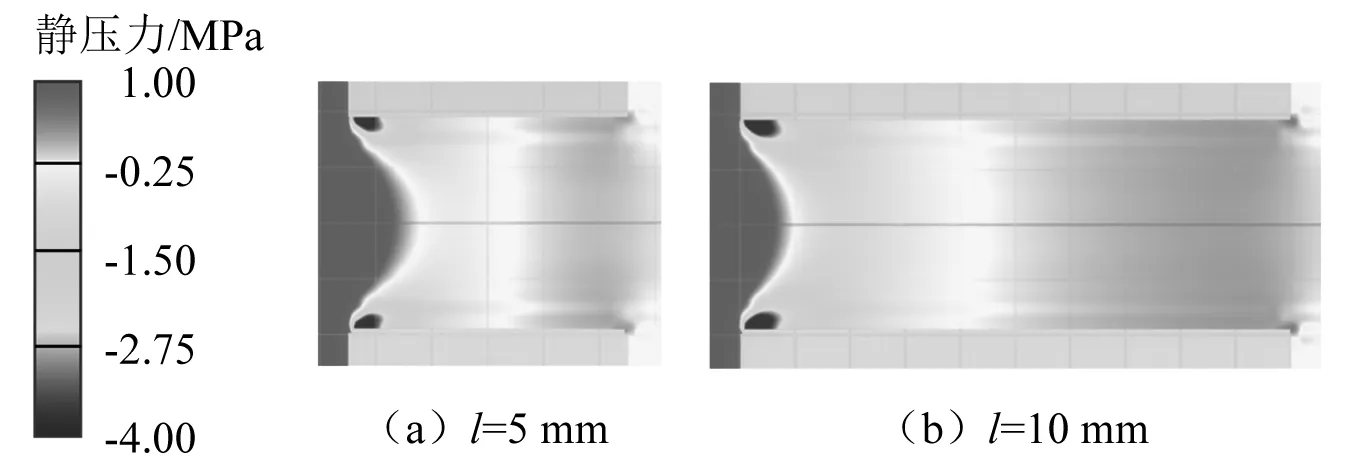
图7 流动附壁前后静压力分布Fig.7 Static pressure distribution before and after flow attached wall

3.3 流孔直径

流孔直径是唯一直接体现在阻尼力计算公式中的流孔几何参数，所以也是唯一在缩流系数工程估算方法中使用到的几何参数，因而流孔直径对阻尼的影响分为直接作用和间接作用，间接作用指的是流孔直径对缩流系数的影响。考虑缓冲器流孔直径尺寸设置和对阻尼力大小的变动区间，分别选取流孔直径为3.4 mm，3.6 mm，3.8 mm，4.0 mm和4.2 mm的流孔进行计算。得到阻尼力与压缩速度曲线和缩流系数与压缩速度曲线如图8所示。

图8 各流孔直径阻尼性能随压缩速度变化曲线Fig.8 Variation curve of damping performance with compression velocity for each diameter of oil hole

图8(a)对比了各流孔直径阻尼力计算结果，阻尼力随着流孔直径的增大而减小。流孔直径减小0.2 mm，阻尼力最大增加了1.96 kN，并且随着流孔直径的减小，相同直径差产生的阻尼力差值逐渐增大。图8(b)中对比了各流孔直径缩流系数计算结果，缩流系数随流速增加先增大后减小，随流孔直径变化在三个区域内呈现不同的规律。在图中左侧区域，缩流系数随流孔直径增大总体呈增大趋势，说明压缩速度较低时，孔内流动速度相应较小，流动没有发生分离，所以流动的有效面积随着流孔的增大相应的增加。中间区域缩流系数随流孔直径增大呈减小趋势。在图中右侧区域，压缩速度继续增加，缩流系数随流孔直径增大呈增大趋势，同左侧区域变化趋势一致。

压缩速度增加使得流孔内部流速相应增大，流孔内部流动由层流逐渐过渡为湍流，转变发生的临界压缩速度与孔内流速相关。孔内截面理论平均流速随缓冲器压缩速度变化趋势如图9所示，孔内流速随着压缩速度呈线性变化，直径较小的油孔孔内流速更大。孔内流动在更低的压缩速度下就转变为湍流，缩流系数也随着流动特性产生变化。故在图8(b)中部区域小直径流孔缩流系数首先增大，在右侧区域缩流系数首先减小。

图9 理论平均流速分布Fig.9 Theoretical average flow velocity distribution

图10对比了各流孔直径下缩流系数随流孔截面理论平均速度变化趋势，除了在低流速区域中的不同，各流孔的变化趋势基本一致。当理论流速低于40 m/s时，缩流系数随着流孔直径增大而减小。当理论流速大于40 m/s时，各流孔缩流系数曲线基本重合，说明在孔内流速较大时，流孔直径对缩流系数的影响仅限于改变了同压缩速度下的孔内流速，而不同直径在有限区间内的变化对缩流系数几乎没有影响。

图10 缩流系数随理论平均流速变化曲线Fig.10 Variation curve of discharge coefficient with theoretical average flow velocity

3.4 后端压力

工程估算方法中没有考虑后端压力，且缓冲器行程变化过程中，气腔压力持续变化，对流孔流动特性产生影响。考虑起落架气腔初始充填压力和工作最大压力，分别选取后端压力0.5 MPa，1.5 MPa，2.5 MPa和3.5 MPa进行计算，得到阻尼力与压缩速度曲线和缩流系数与压缩速度曲线如图11所示。

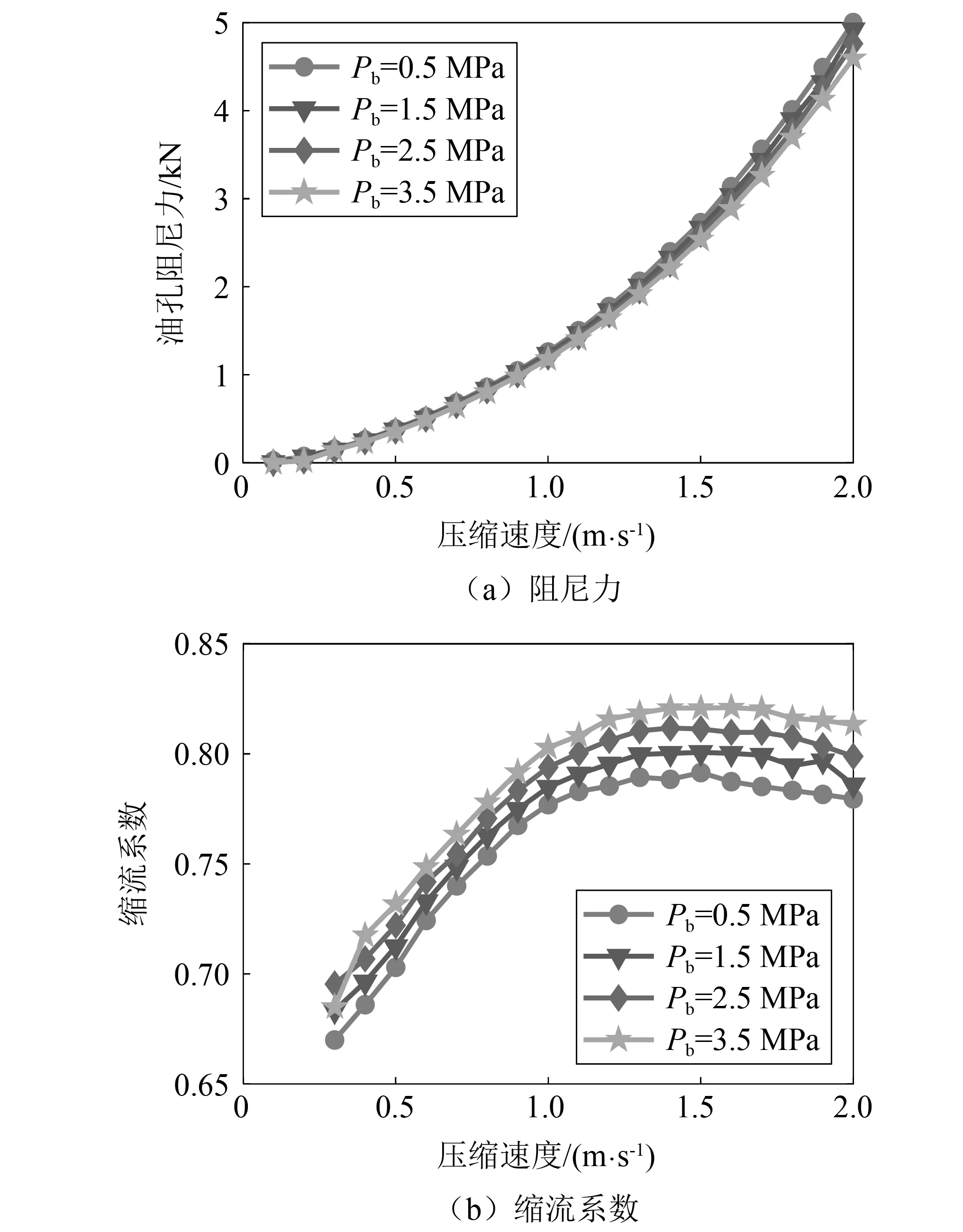
图11 各后端压力阻尼性能随压缩速度变化曲线Fig.11 Variation curve of damping performance with compression velocity for each backpressure

不同后端压力下阻尼力在低压缩速度时的差异很小，在较高压缩速度时，开始出现明显的差异，阻尼力随着后端压力增大而减小。缩流系数随压缩速度增大先增大后减小，且在各个压缩速度下随后端压力增大均呈增加趋势，随压缩速度增加缩流系数变化规律基本一致。在低压缩速度时，各后端压力下缩流系数间的差距小于在较高压缩速度下的间距。后端压力主要影响流动分离的临界条件，后端压力越大流动越不容易发生分离，则流动特性更有利于流体通过流孔，导致更小的阻尼力和更大的缩流系数。流动分离产生的情况随着流速的不断增加而变得严重，所以在高流速情况下，由于后端压力增加产生的改善流动特性的效果则更明显，体现在缩流系数增长的更多。

4 回归方程及验证

上述通过对LBM计算结果的分析，得到了各参数对流孔缩流系数的影响结果，然而单参数的敏感性分析结果不能直接用于缓冲器流孔设计，需要将各参数对阻尼性能的影响表示成统一的形式，用于阻尼力计算中。

选择流孔长度、流孔直径、后端压力和压缩速度作为设计变量，选择流孔处阻尼力作为目标值，考虑参数个数和研究水平个数基本处于较低的数值，使用全因子试验方法，利用LBM计算样本点处阻尼力数值。各设计变量取值范围根据上述分析中使用的结构参数基础值进行确定，选取的各参数设计区间如表3所示。

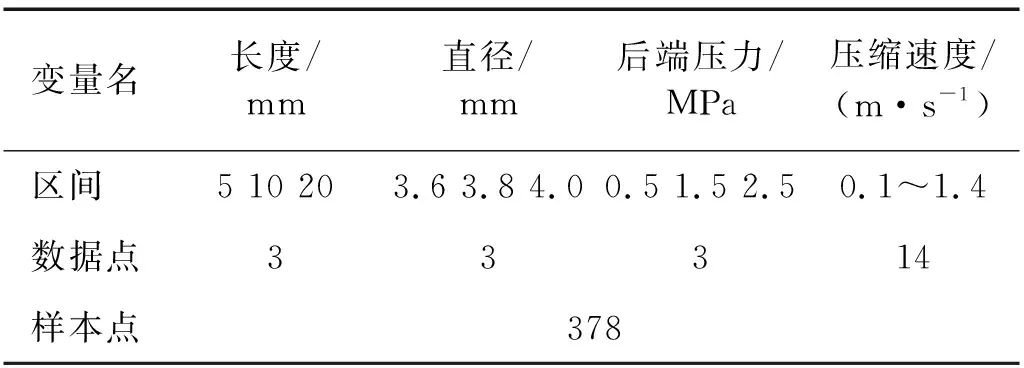
表3 阻尼力变量设计区间Tab.3 Interval of design variables for damping force

样本点数据计算在搭载了两个CPU的计算机上执行，CPU型号为Intel Xeon E5-2650 v4，每个CPU含有12核心24线程，378个样本点数据的计算时间总共为68 h。基于最小二乘法拟合得到了阻尼力回归方程，均方根误差为41.3，R2为0.997,说明回归方程的拟合精度可靠。图12中样本点数据分布与45°对角线相对位置也说明了回归方程的准确度。上述对比结果说明了回归方程在参数区间内可以被用于阻尼力的计算，结合数值优化方法，可以得到使得起落架缓冲性能最优的油孔结构参数。

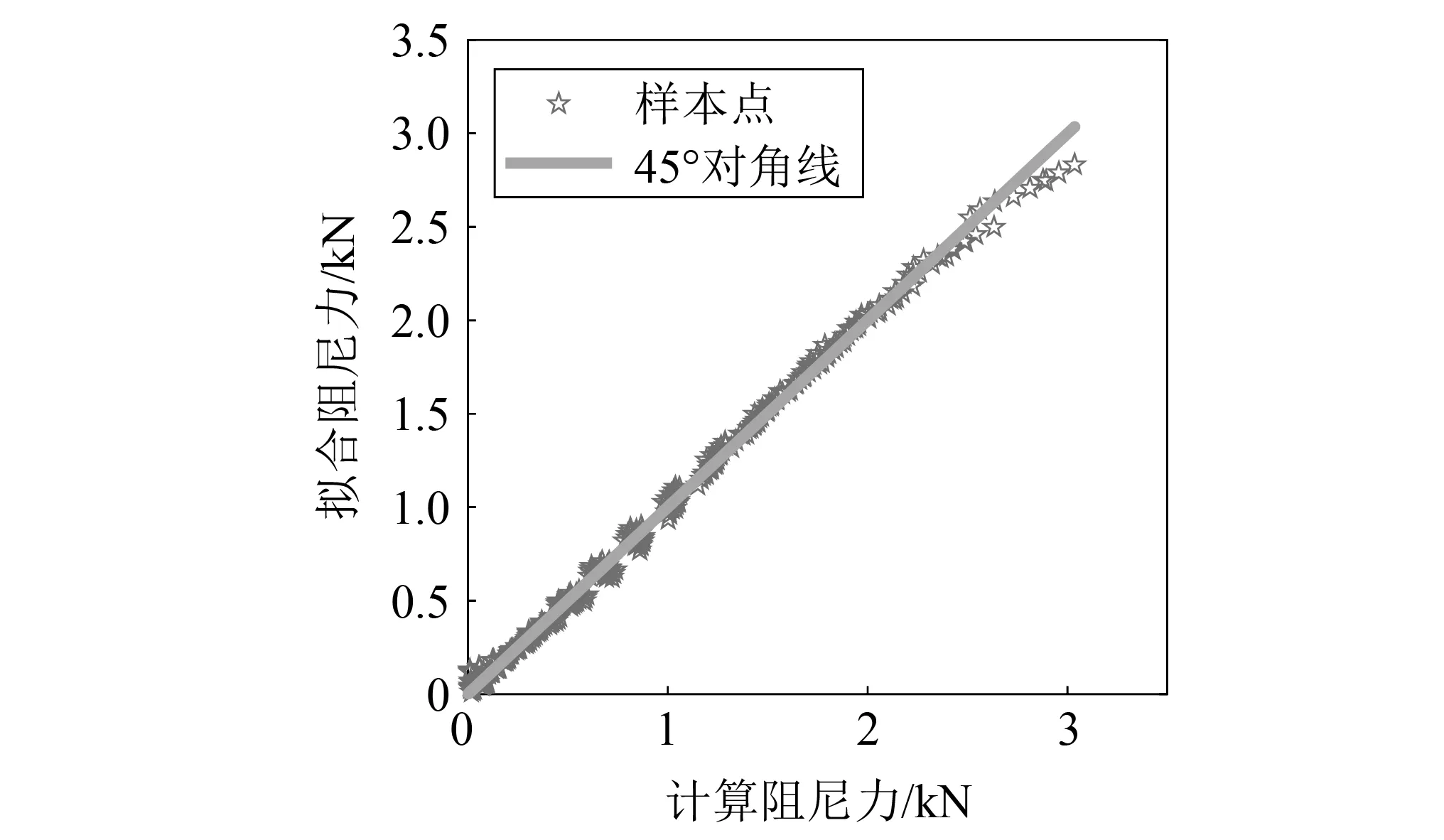
图12 样本点数据分布Fig.12 Sample points data distribution

5 结 论

主要结论如下：

(1)格子Boltzmann方法计算得到的阻尼力与试验值最大相对误差不超过5.48%，说明格子Boltzmann方法在分析直角圆柱孔流动特性中的准确性，可以用于对起落架油孔阻尼性能的分析中。

(2)油孔长度会改变流动最小收缩截面与油孔的相对位置和流动沿程阻力，从而对阻尼性能产生影响；油孔直径对阻尼力影响最大，对缩流系数的影响仅限于改变了同压缩速度下的孔内流速，而油孔直径在有限区间内的变化对流动特性几乎没有影响；后端压力增大会减缓油孔内部流动分离，增大各压缩速度下的缩流系数。

(3)阻尼力关于油孔长度、油孔直径、后端压力和质量流量的回归方程具有较高的拟合度，能够用于参数区间内的阻尼力计算，说明格子Boltzmann方法对阻尼性能的分析能够被应用在一般性的起落架缓冲器油孔设计中。