四足机器人腿部结构设计与分析

胡家信 秦海鹏 朱小明

四足机器人腿部结构设计与分析

胡家信 秦海鹏 朱小明

（长安大学工程机械学院，陕西 西安 710064）

为了提高四足机器人的能量密度和在复杂地形下的机动性，文章设计了一种具有四自由度的四足机器人单腿结构。首先，参考哺乳动物的腿部仿生拓扑结构，搭建了四足机器人的单腿三维模型。其次，通过DH模型法，对其进行正逆运动学分析，求解机构的正逆运动学方程。之后，根据求得的正向运动学方程，利用matlab对机器人足端的运动空间进行分析，绘出足端运动空间云图。最后，通过速度分析和静力学分析，得出机器人各个关节的额定转矩，验证该机构的可行性。

四足机器人；结构设计；运动学分析；静力学分析

引言

随着人类文明的进步，人们在执行一些危险性较高、难以执行的任务时，更希望通过机器人代替人们来执行，如在抗震救灾、高空作业、污染土壤水质取样等许多方面。其中，四足机器人凭借其优越的避障能力，高效的机动性，超高的灵活性，越来越受到人们的青睐[1]。然而目前四足机器人的负载重量较低，速度较慢，其性能有待进一步提高，机械腿作为四足机器人的重要基础部件，决定了四足机器人的核心应用性能，当前大多数机械腿在冲击和推进状态下的机械强度、能量效率、总功率密度、载重量比等性能指标都不理想[2]。为此，本文设计了一款高机动性和高能量效率的机械腿，旨在解决上述问题。

1 机器人的腿部总体结构设计

常见的四足机器人的腿部结构主要有关节腿和棱柱腿，棱柱腿型的腿部结构顾名思义由诸多连杆相互铰接而成，腿部结构简单、轻巧，惯性很小[3]。然而，这种类型的腿由于旋转关节较少而限制了自身的运动性能，这导致了其对地形的适应性不足。与棱柱腿相比，关节腿采用旋转关节代替直线棱柱关节来实现腿长控制，具有良好的几何拓扑仿生性、更好的运动性能、更大的自稳速度域、更宽的腿脚运动空间和更高的能量效率。它在复杂地形适应和障碍物穿越方面显示出更大的优势。因此，本文采用了关节腿的形式，设计了如图1所示的四自由度（两个主动自由度和两个被动自由度）四足机器人单腿模型。

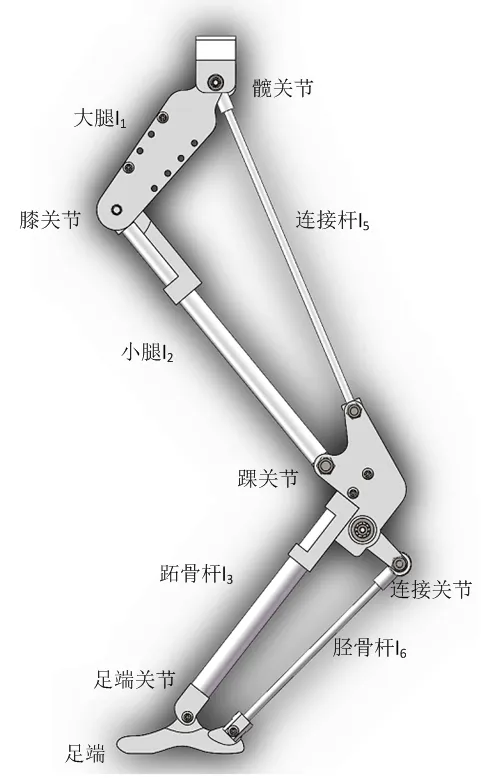
图1 四足机器人单腿三维模型图

图1中，分别在单腿的髋关节、膝关节设计了一个主动的转动自由度，用于控制腿部的运动；跖骨杆、大腿杆、小腿杆以及连接杆形成了一个四杆机构，使踝关节变成了一个被动关节，跟随髋关节和大腿关节的转动；胫骨杆、足端和跖骨杆也是一个四杆机构，当足端与地面接触时，足端的位置自动跟随地面，这样连接关节也将被动确定，因此，足端关节也是一个被动自由度。在杆长的确定方面，结合实际应用需求以及四杆机构运动原理，选定大腿杆有效长80 mm，小腿杆有效长164 mm，跖骨杆有效长122 mm，连接杆的长度决定了整个机器人腿部能否达到预期位置，由于各个关节均没有周转副，双摇杆机构即可满足需求，选定连接杆的有效长为176 mm。

2 单腿运动学分析

机器人的运动学分析就是在不考虑机构所受力的情况下，分析系统的运动特性。具体来说就是描述末端执行装置与中间各杆件之间的运动学关系，一般可分为两大类：正向运动学与逆向运动学。

正向运动学就是在已知机器人运动的各杆件的几何信息和关节变量的情况下，将一个个坐标系固结在各个杆件上，最终求解从固定不动的基础坐标系变换到与末端执行装置固结的坐标系的变换过程。反之，所谓逆向运动学就是在已知从基础坐标系变换到末端执行机构的坐标系的情况下，来求解中间各个关节变量[4]。

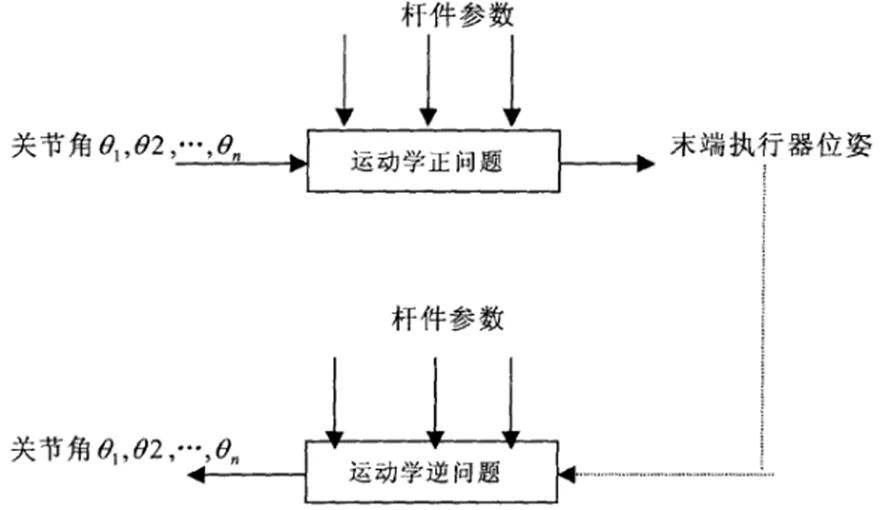
图2 正向运动学与逆向运动学转换关系图

本文的符号描述如下：

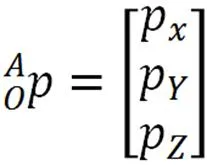
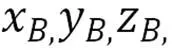
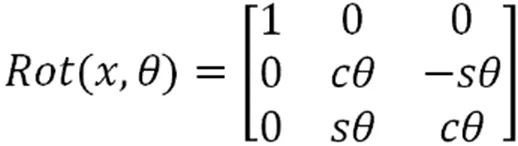
绕y轴旋转的旋转矩阵为：

绕z轴旋转的旋转矩阵为：

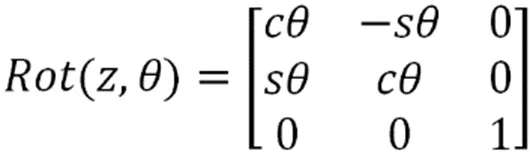
为了将平移变换和旋转变换结合起来，可以用齐次变换矩阵综合表示：

2.1 基于DH模型法的正向运动学求解

机器人正向运动学的求解方法的一般方法是DH模型法，即在机器人腿部结构图上建立DH坐标系（如图3所示），然后将相关的参数列于DH Table中，进而根据DH Table中的数据，求解齐次变换矩阵，最终列出末端执行装置相对于基础坐标系的正向运动学方程[5]。

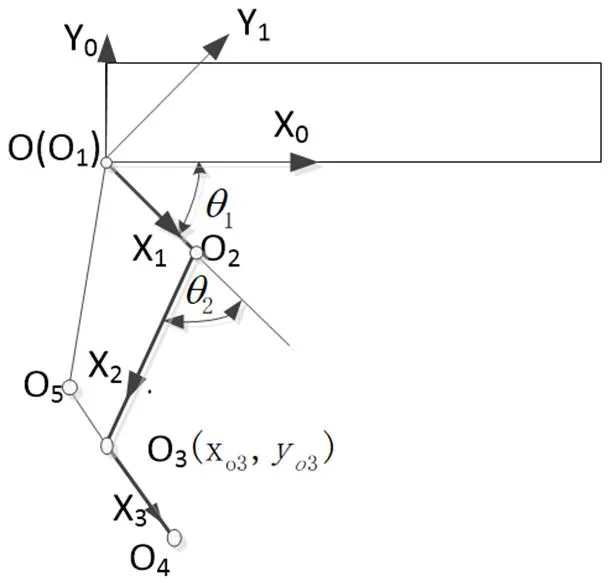
图3 机器人腿部的DH坐标系

根据DH模型法求解过程，将有关的DH参数列于表1中，其中，α-1为相邻两个Z坐标的扭角，a-1为相邻两个Z坐标的公法线的长度，d为相邻两个X坐标在Z方向上的距离，θ为相邻两个X坐标的夹角。

表1 单腿DH参数表

由坐标系变换的链式法则，可得出坐标系{i-1}到坐标系{i}的齐次变换矩阵为：

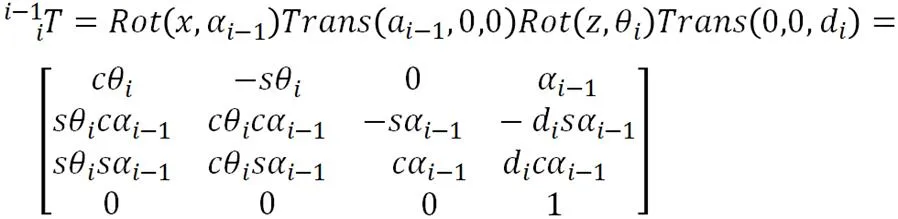
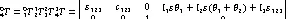
以上公式中1，2，3均为腿部各个杆件的长度，1，2，3为各关节处各个杆件的转角。

2.2 逆向运动学分析

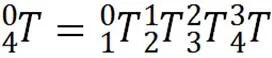
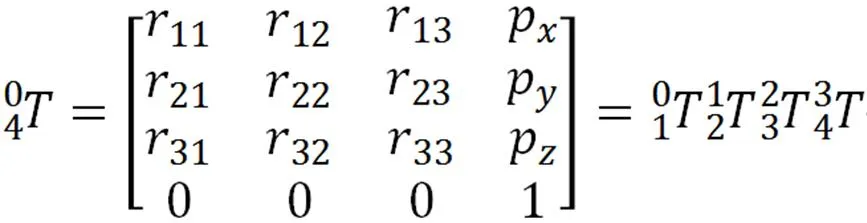
2.2.1 求解1

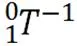
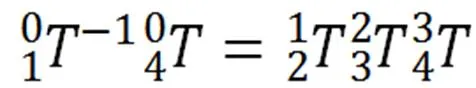
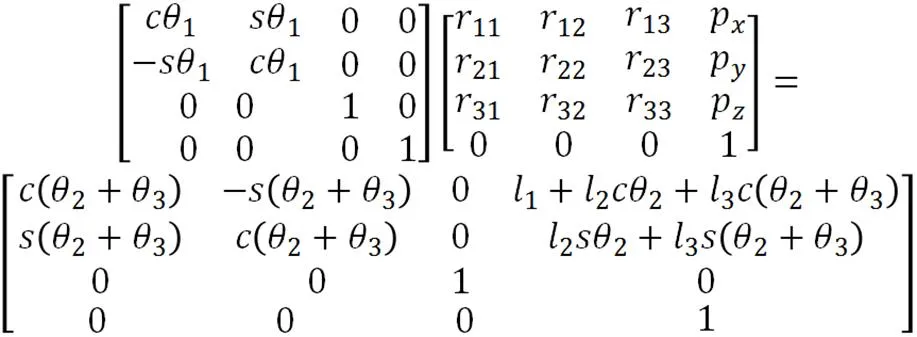
令两式相等，可得：

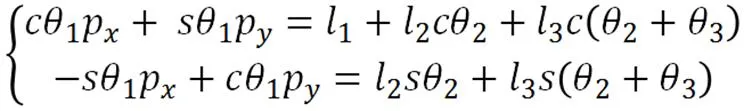
将上式方程左右两边同时平方后，再相加整理可得：

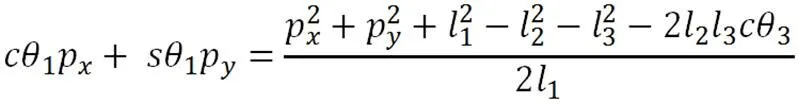
为了求解式（7），可以利用三角代换得式（8），

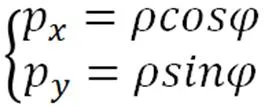
其中，(,)是2幅角反正切函数。

将式（8）带入式（7），并根据正弦函数与余弦函数之间的平方和为1的关系，可得式（9）如下：

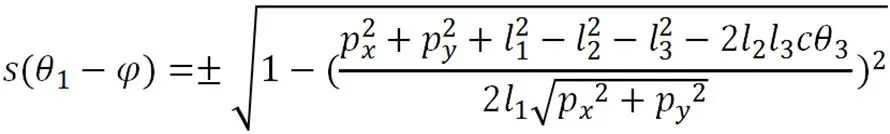
于是可令：

化简后可得到1：

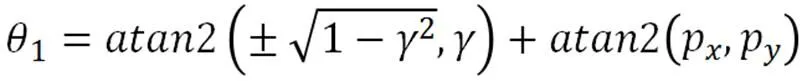
上式中的正负号分别对应两个1的可能解，可根据机器人实际位置进行取舍。

2.2.2 求解2

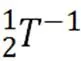
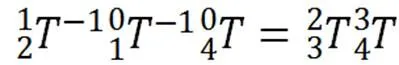
令矩阵方程左右两边的元素分别对应相等可以得到式（12）如下：

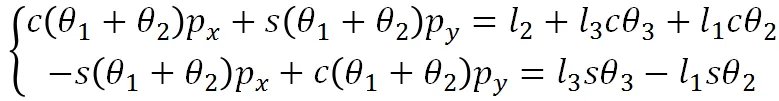
之后解法可参照求解1的过程，令式（12）方程左右两边同时平方后相加整理化简后可得下式：

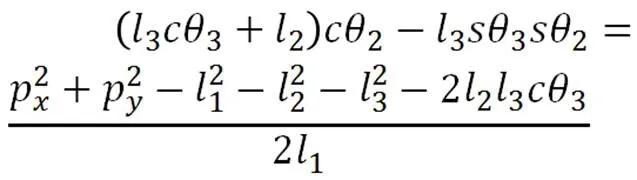
利用三角代换可得：

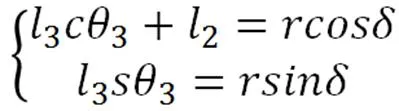
式中

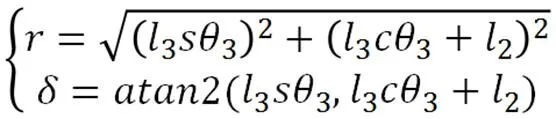
将式（14）带入式（13）可得式（16）和（17）如下：

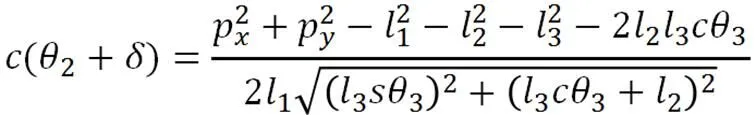
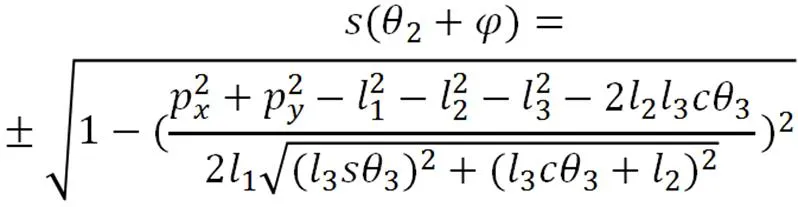
令

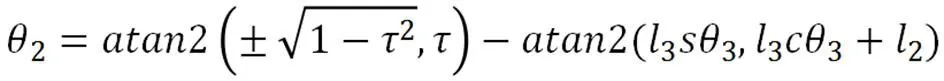
上式中，正负号分别对应2的两个可能解，可根据机器人实际位置进行取舍。

2.3 利用蒙特卡罗法分析足端运动空间

为了能够更好地分析四足机器人在运动时足端所能达到的空间，需要对足端进行运动仿真分析，以便进一步验证结构设计时的合理性。足端空间分析在这里选择的是蒙特卡罗分析法，首先，根据机器人腿部结构的正向运动学，选定1，2，3为变量，并确定各个变量的取值范围：

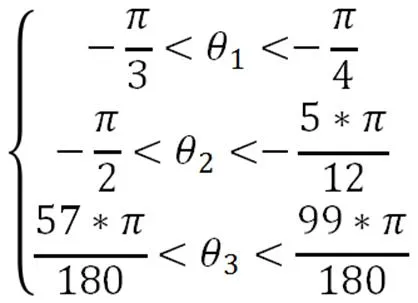
随后，为每个变量抽取随机数，使变量包含于以上范围中，并带入正向运动学方程，即可求得一个足端在笛卡尔坐标系下的坐标位置。将这个过程重复1 000 000次，可以得到足端运动空间云图如图3所示。

图3-坐标系下的足端运动空间图

由图3可知，足端在髋关节处的基础坐标系中所能达到的位置主体大多位于轴之下，且基本关于坐标系对称，基本符合哺乳动物后腿足端运动的要求。

3 静力学分析与额定扭矩计算

为了合理的选择关节处的驱动器，首先要对四足机器人的腿部进行速度分析，得到从笛卡尔坐标系映射到关节坐标系的雅可比矩阵，其次进行静力学分析，根据机器人腿部所受的足端力和足端速度，通过雅可比计算出所需的关节力和关节速度，据此选择合理的关节驱动器。

3.1 速度分析

速度分析是研究机器人运动的基础，它同运动学分析一样，也分为正解和逆解，从关节坐标系下的转动速度计算出笛卡尔坐标系下的运动速度称之为速度分析的正解，反之，从笛卡尔坐标系下的运动速度计算出关节坐标系下的关节转动速度称之为速度分析的逆解。

在本此设计中，髋关节和膝关节是主动自由度，踝关节处的运动通过四杆机构可以被动确定，因此，速度分析和静力学分析时，只需要计算髋关节和膝关节处的速度和所受的外力即可。

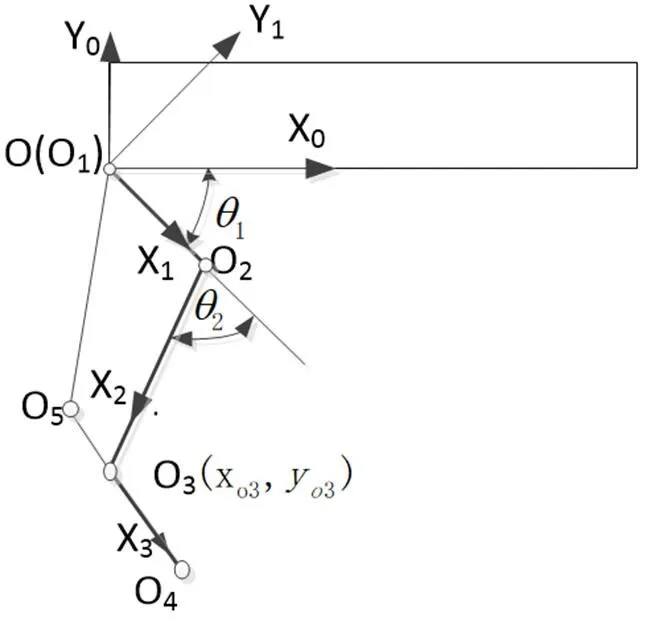
图4 四足机器人速度分析示意图

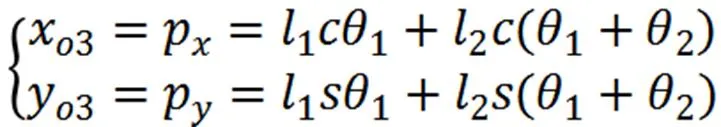
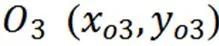
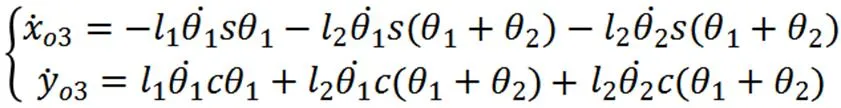
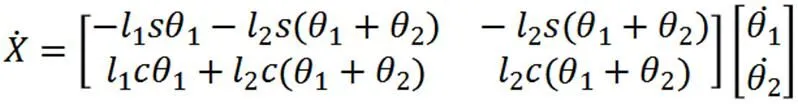
此处可令

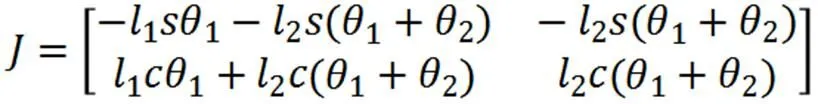
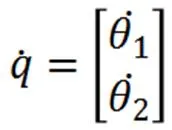
这里，J为雅可比矩阵。由此，式（21）可以简化为：

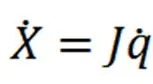
上式便是四足机器人腿部结构速度分析的正解，而速度分析的逆解便是在式（23）等式左右两边同时左乘雅可比矩阵的逆，即可得到速度分析的逆解：

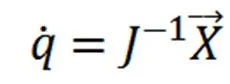
3.2 静力学分析

机器人的静力学分析的是指机器人在静止或者低速运动的情况下，研究机器人各部分杆件所受的外力或者各杆件之间的相互作用力[6]。本文中，主要根据机器人所受的足端力来求解各关节所需的驱动力矩。图5为本文的四足机器人单腿结构的静力学受力分析简图。

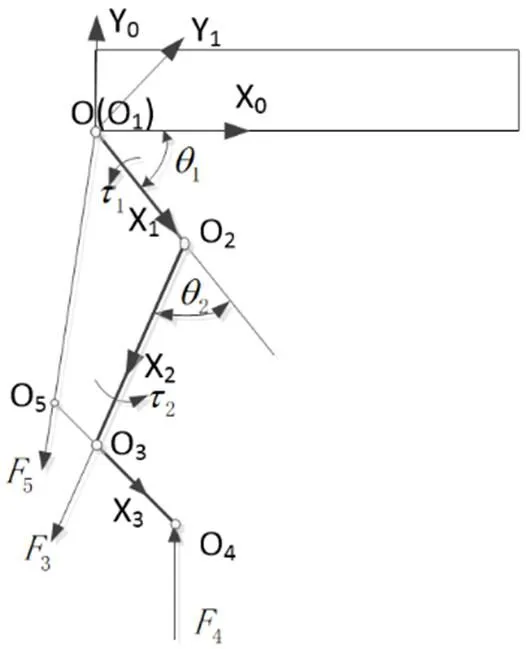
图5 四足机器人单腿静力学分析图

根据图5所示，四足机器人的足端受到来自地面对其的支撑反力，其大小和方向均已知，方向沿杆方向，其竖直方向上的分力大小等于机器人承受的载荷。为了方便求解膝关节、髋关节处所需的驱动力矩，可以将大腿杆、小腿杆分离出来单独分析，其受力如图6所示。

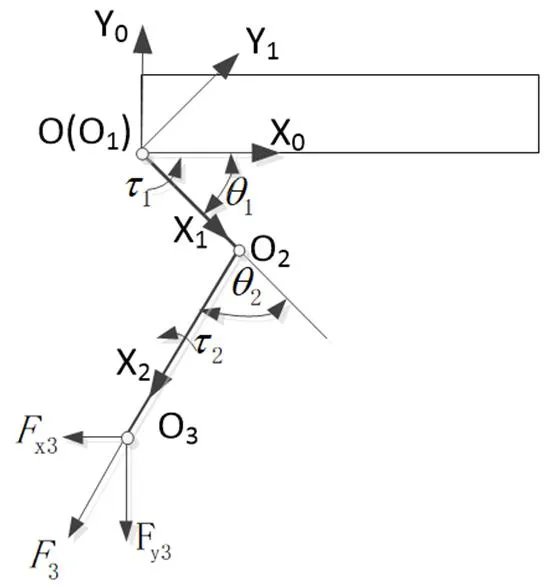
图6 四足机器人单腿部分结构受力分析简图

根据虚功原理，处于平衡状态下的物体总虚功为零，得：

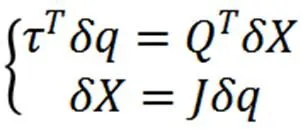
上式方程左右两边同时积分并简化可得：

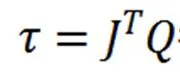
上式中，J为雅可比矩阵，展开得：

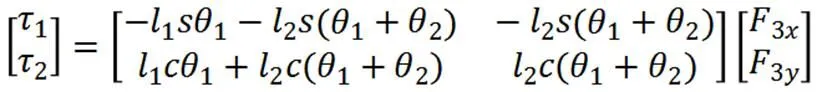
将具体数据代入计算可得，假定承载要求为20 kg，在静止的情况下，单腿的承载能力最大为5 kg，再将足端载荷转换到踝关节处可得踝关节的受力为3。因此，通过在3左乘雅可比矩阵的转置可得髋关节和膝关节的额定扭矩为：

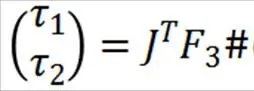
其中J为雅可比矩阵得转置。

4 结束语

本文首先根据实际运用需求确定了机器人腿部的总体结构和大致尺寸，利用solidworks对机器人腿部进行三维建模。其次，利用DH模型法对其进行正逆运动学分析，求解机构的正逆运动学方程。之后，根据求得的正向运动学方程，利用matlab对机器人足端的运动空间进行分析，绘出足端运动空间云图。最后，对四足机器人单腿进行速度分析和静力学分析，得出机器人各个关节的额定转速和额定转矩。因此，本文对设计的四足机器人单腿进行了充足的理论分析，具有很高的可行性，更好的几何拓扑仿生性，运动性能，更大的自稳速度域，更宽的腿脚运动空间和更高的能量效率，它在复杂地形适应和障碍物穿越方面显示出更大的优势。

[1] HYUN D J, SEOK S, LEE J, et al. High speed trot-running: Implementation of a hierarchical controller using proprioceptive impedance control on the MIT Cheetah[J]. International Journal of Robotics Research, 2014, 33(11): 1417-1445.

[2] 李鹏飞. 四足机器人结构设计与运动学仿真分析[D]. 昆明: 昆明理工大学，2019.

[3] 马宗利，刘永超，朱彦防，等. 奔跑四足机器人腿结构设计与分析[J]. 东北大学学报(自然科学版)，2016，37(9): 1305-1310.

[4] SEN M A, BAKIRCIOGLU V, KALYONCU M. Inverse kinematic analysis of a quadruped robot[J]. International Journal of Scientific and Technology Research, 2017, 6(9): 285-289.

[5] 张千伟，张龙. 仿生四足机器人结构设计与运动学分析[J]. 兵工自动化，2017，36(5): 73-76.

[6] WANG H, SANG L, HU X, et al. Kinematics and dynamics analysis of a quadruped walking robot with parallel leg mechanism[J]. Chinese Journal of Mechanical Engineering, 2013, 26(5): 881-891.

Design and Analysis of Leg Structure of Quadruped Robot

In order to improve the energy density and maneuverability of the quadruped robot in complex terrain, a single-leg structure of the quadruped robot with four degrees of freedom is designed in this paper. Firstly, referring to the mammalian leg bionic topology, a single-leg 3D model of the quadruped robot is built. Secondly, the forward and inverse kinematics of the quadruped robot are analyzed by DH model method, and the forward and inverse kinematics equations of the mechanism are solved. Afterwards, according to the obtained forward kinematics equations, use matlab to analyze the motion space of the robot foot, and draw a cloud map of the foot motion space. Finally, through speed analysis and static analysis, the rated torque of each joint of the robot are obtained to verify the feasibility of the mechanism.

quadruped robot; structural design; kinematics analysis; statics analysis

TP242

A

1008-1151(2022)11-0001-05

2022-08-23

胡家信（1997－），男，长安大学工程机械学院在读硕士研究生，研究方向为机器人控制。