AlxCoCrFeNi 拉伸力学性能的分子动力学模拟

张 荣，祁文军，张 爽

（新疆大学机械工程学院,新疆 乌鲁木齐 830047）

0 引言

随着时代发展和科技进步，对航空航天、石油化工等工程领域应用的高温金属材料提出了更为严苛的要求。高熵合金（HEAs）因具有高熵效应、严重的晶格畸变效应、迟滞扩散效应，被认为是一种极具潜力的新型金属结构材料[1−6]。

HEAs 元素的复杂性及其熔点的巨大差异，使其制备成本高，加工条件苛刻，亟待进一步的研究。目前，公开报道的HEAs 种类与理论上的HEAs 体系种类相差较大，需要采用理论模拟和计算避免HEAs 纷繁复杂的成分试验研究。

分子动力学（Molecular dynamics，MD）可从微观探索材料变形机制，并从原子层面揭示宏观现象。近年来，许多研究者采用分子动力学对HEAs 材料的拉伸力学性能、微观结构演化等进行了大量的研究[7−15]。Li 等[7]采用分子动力学方法模拟单轴拉伸发现AlCrFeCuNi1.4具有超高塑性，其微观机制是孪晶和层错的产生和生长提高了材料塑性。张路明等[8]采用分子动力学模拟发现温度对AlxCoCrFeNi 的净效应类似于晶格畸变。Afkhama 等[9]研究表明AlxCrCoFeCuNi 的屈服应力随着温度的升高而下降，合金均有超塑性行为。Li Jia 等[10]研究表明，高冷却速率下（1014K/s）AlCoCrCuFeNi HEAs 趋向形成强度低的玻璃组织，但是会产生稳定的应力流；低冷却速率下（1012K/s）AlCoCrCuFeNi HEAs 会出现结晶，强度较高，但是会出现“软化”。此外，对CoCrFeMnNi[11]，AlCoCrCuFeNiSi[3]，AlCoCrCuFeNiMo[12]也有较多研究。

由于AlCoCrFeNi HEAs 的优异性能[13−16]，研究者对其开展试验研究并取得了部分成果。Wang 等[17]观察了AlCoCrFeNi HEAs 准静态压缩和动态压缩下的应变硬化行为，发现合金具有高应变速率敏感性。Zhang 等[18]观察了AlCoCrFeNi HEAs 在低温段从298 K 降温到77 K 时的抗拉强度，发现其抗拉强度随着温度的下降而上升，延展性呈相反趋势。近年来，关于应变速率和温度对金属材料性能影响的研究较为深入，也对HEAs 进行了部分探索，但物理试验中应变速率相对较低，并且在某些情况下涉及的温度范围很窄。随着高熵合金在航空航天、石油化工等工程领域的应用，对其在高温和高应变速率下的力学性能提出更高要求，但目前尚未见有关这方面的研究报道。

笔者采用分子动力学方法定量研究了Al 摩尔比0.1 至1.0 时Al 含量、高温和高应变速率下AlxCoCrFeNi HEAs 单轴拉伸时材料内部的微观结构演变、径向分布函数（Radial distribution function，RDF）变化与位错演化，进而揭示上述因素对宏观力学性能的影响机理，为新材料研发提供一定的理论指导，分子动力学的应用有助于提高新材料开发效率。

1 建模及仿真方法

采用LAMMPS[19]软件建立AlxCoCrFeNi（x为摩尔比，x=0.1，0.3，0.5，0.7，1.0）分子动力学模型。其中AlxCoCrFeNi 晶格常数为α=0.357 nm[20]，利用晶体学理论知识，首先建立尺寸为20α×40α×20α（α为晶格常数）的体心立方（BCC）原子模型，按照计算好的比例将铝、钴、铬、铁和镍原子随机填充到原子模型中，建立Al0.7CoCrFeNi、Al1.0CoCrFeNi 原子模型，如图1 所示，在模型中，x，y和z坐标分别为[100]，[010]，[001]晶向，模型原子总数为64 000 个。然后通过替换Al 原子的比例以及晶格类型（FCC），分别建立Al0.1CoCrFeNi、Al0.3CoCrFeNi、Al0.5CoCrFeNi 原子模型。在x、y、z方向均采用周期性边界条件，采用Norse/Hoover 热浴法对系统进行温度控制，整个拉伸过程都执行0.001 ps 的时间步长，采用NPT 系综以0.085 K/fs 的加热速率模拟HEAs 在300～2000 K 的熔化过程及淬火过程[21]，充分弛豫（20 ps）使体系总能量降到最低，确保系统在加载前达到平衡状态。弛豫完成后，采用NVT系综在Y=[010]方向上对原子模型进行单轴拉伸，模拟过程中每隔100 步记录原子在各方向的应力、势能、动能及原子位置。利用后处理软件OVITO对系统输出数据进行数据后处理，通过共近邻分析（CNA）和位错分析（DXA）分析原子的结构演变和位错变化。设置不同的拉伸温度分组讨论，研究温度对拉伸性能的影响，其中控制的温度分别为300，500，700，900，1 000，1 100，1 300，1 500 K。设置不同的应变速率研究应变速率对拉伸性能的影响。应变速率[22]及对应弛豫时间如表1 所示。

表1 HEAs 应变速率及弛豫时间Table 1 tensile strain rate and relaxation time of HEAs

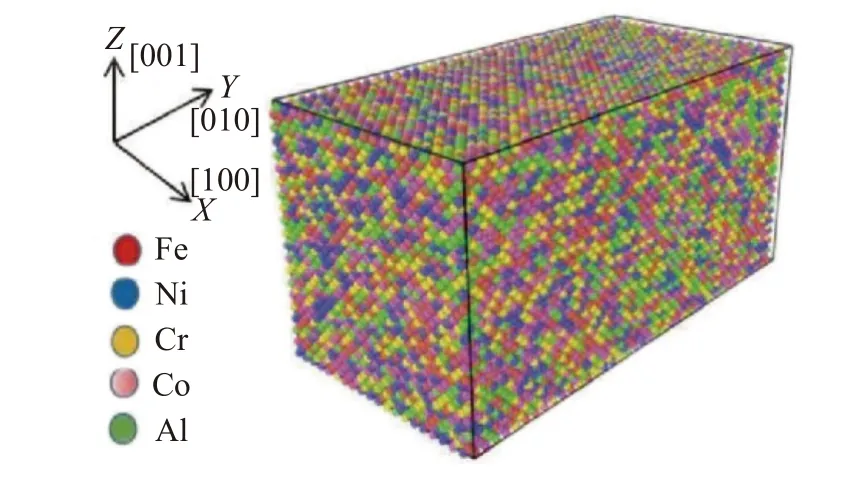
图1 Al1.0CoCrFeNi HEAs 模型及原子示意Fig.1 Model and atomic structure of Al1.0CoCrFeNi HEAs

在AlxCoCrFeNi HEAs 模型的后续相关计算中，采用嵌入原子势（Embedded-atom method，EAM）描述 Al-Co-Cr-Fe-Ni 之间的相互作用。嵌入原子势[23]的计算公式如式（1）（2）所示：

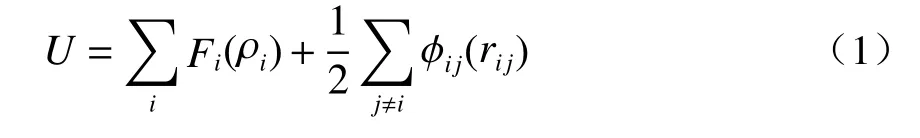
式中，U为系统的总势能；F为嵌入能函数，是原子的电子密度ρ的函数；ρi表示除原子i外其余原子在原子i处产生的电子云密度之和；Øij为对势项；rij为第i个原子与第j个原子之间的距离。

2 结果与分析

2.1 拉伸力学性能

图2 为Al1.0CoCrFeNi HEAs 原子模型在温度为300 K、应变速率为1×1010s−1下Y 方向单轴拉伸的应力-应变曲线。截取4 个节点的原子结构图，其中绿色代表FCC 结构，蓝色代表BCC 结构，红色代表HCP 结构，白色代表Other 原子。从图2 可知，Al1.0CoCrFeNi 原子模型的拉伸变形经历了弹性变形、屈服、塑性变形三个阶段。拉伸初始阶段，应力-应变服从广义胡克定律，对0～14.9%应变段应力-应变曲线数据拟合，得杨氏模量E为105.46 GPa。该应变段原子结构以BCC（蓝色）为主，并出现少量的FCC（绿色）和无序原子（白色），表明弹性变形阶段相比较单一。继续增加载荷，应变达到14.9%时，应力达到极大值15 GPa，FCC 和Other 原子显著增加，并出现少量的层状HCP 相，各原子堆层较均匀。随后应力随应变增大大幅下降，材料进入不均匀塑性变形阶段，原子模型出现了大量非晶化，此时以Other 原子为主，原子模型的内应力得到释放，导致材料强度出现断崖式下跌。进一步变形过程中，Other 原子、FCC、BCC、HCP 之间相互转化，BCC原子数目先减少后增加，层状HCP 相增加，并且主要沿着45°以及135°方向排列。FCC 密排面原子错排层大于两层是孪晶结构，小于或者等于两层是堆垛层错，孪晶和层错的产生可以加强材料的塑性。孪晶和层错的形成会导致原子模型出现应力松弛，致使应力大幅降低，且下降速率与原子模型中孪晶和层错的产生速度有关。此外，研究人员对AlCr-FeCuNi[7]与Al0.1CoCrFeNi[8]的实验研究发现了孪晶与层错，这与本研究模拟结果一致，说明本研究的建模及仿真方法正确。

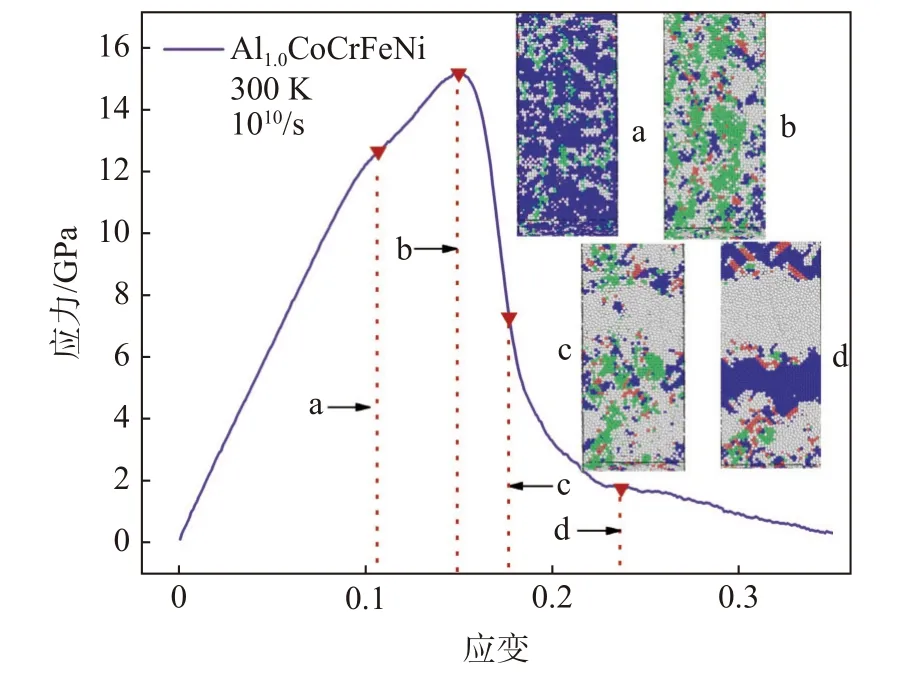
图2 Al1.0CoCrFeNi 拉伸应力-应变曲线Fig.2 Stress-strain relations of Al1.0CoCrFeNi under tensile loading

图3 为300 K 时不同应变率下Al1.0CoCrFeNi高熵合金的径向分布函数和不同晶格含量变化曲线。在图3（a）中可以看出，屈服应变之前（0<ε≤14.9%），每个峰值随着应变的升高而逐渐减小，这表明高熵合金的晶体结构被持续破坏。在达到屈服应变之后（14.9%<ε≤23%），材料的振幅随着应变增大而逐渐增加，这表明在这个阶段，晶体结构开始恢复。由图3（b）中可知，初始弹性变形阶段（0<ε≤5%），原子模型保持着有序的BCC 结构，原子模型中只有极少数的BCC 结构的原子转变为非晶态；达到屈服应变之后，高熵合金发生塑性变形，并且大量BCC 结构的原子转变为其他晶格，这表明高熵合金的塑性变形与材料的相变有关。

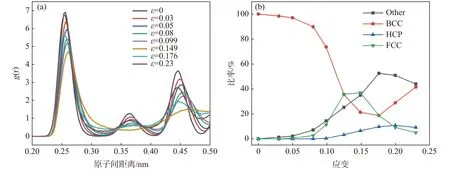
图3 (a)Al1.0CoCrFeNi 在单轴拉伸过程中不同应变下的RDF，(b)BCC，HCP，FCC 以及Other 原子数目随应变的变化Fig.3 （a）The RDF of Al1.0CoCrFeNi HEA at different strains during uniaxial tension,(b) changes of the numbers of BCC，HCP，FCC and Other atom clusters with strain

图4 为不同拉伸应变状态下Al1.0CoCrFeNi HEAs 的位错演化。由图4 可以看出，AlxCoCrFeNi 在拉伸载荷作用下出现的位错类型包括：1/2<110>位 错，1/3<100>位 错，1/3<111>位 错，1/6<110>位错，1/6<112>位错以及一些无法识别的位错，表示为Other 位错。在应变为0<ε≤11.3%的拉伸阶段，1/6<112>位错出现，并随着应变的进行开始增多；当应变为11.3%<ε≤14.9%时，位错总长度急剧下降，结合图3（b）进行对比分析，此时FCC 结构原子急剧增加，说明FCC 结构有助于减少位错的生成，提升材料强度；在应变为14.9%<ε≤19.6%拉伸阶段，1/2<110>位错，1/3<100>位错，1/3<111>位错，1/6<110>位错开始增加，位错与位错之间相互缠绕，由于位错和滑移现象已经启动，使得应力急剧变化，最后趋于平缓。

图4 不同拉伸应变下Al1.0CoCrFeNi HEAs 的位错演化Fig.4 Dislocation evolution of Al1.0CoCrFeNi HEAs under different strains

2.2 Al 含量对AlxCoCrFeNi 拉伸力学性能的影响

为了研究Al 含量对AlxCoCrFeNi HEAs 拉伸力学性能的影响，建立一系列AlxCoCrFeNi HEAs原子模型，x分别取为0.1，0.3，0.5，0.7，1.0，设置温度为300 K，以1×1010s−1应变速率分别对不同Al含量的原子模型进行Y向单轴拉伸，如图5 所示。

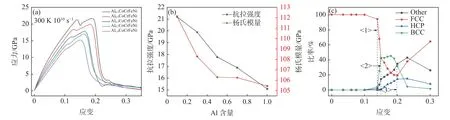
图5 （a）AlxCoCrFeNi 应力-应变曲线，（b）AlxCoCrFeNi 屈服应力和杨氏模量曲线，（c）Al0.1CoCrFeNi 中FCC，HCP，BCC 以及Other 原子数目随应变的变化Fig.5 (a) The stress-strain curve of AlxCoCrFeNi HEAs,(b) The Young’s Modulus and yield stress of AlxCoCrFeNi HEAs as a function of Al concentration,(c) variation of the numbers of FCC,HCP,BCC and Other atom clusters with strain of Al0.1CoCrFeNi

从图5（a）中可以看出，AlxCoCrFeNi 的拉伸过程都经历弹性、屈服、塑性变形阶段，从图5（b）中可以看出，屈服应力和杨氏模量随着Al 含量的增加而降低，每条曲线从弹性阶段到塑性阶段都经历了一个明显的下降过程，且下降速率随着Al 含量的增加而降低。结合微观结构可知，随着Al 含量的增加，原子模型会在更小的应变处开始屈服，更早进入屈服阶段。其中Al0.1CoCrFeNi 在初始弹性阶段（0<ε≤13.9%），每个原子都围绕在平衡位置运动，原子模型保持了FCC 的有序结构，但是只有极少数的原子由于较高的表面能而发生相变，转变为BCC 结构。在屈服阶段（13.9%<ε≤15%），FCC 原子数量急剧下降，同时BCC 原子以及Other 原子数量急剧上升，应力-应变曲线呈下降趋势，这表明激烈的相变导致原子模型内部原子平衡遭到破坏。随着应变继续增大，BCC 原子和Other 原子增加速率减缓，HCP 原子逐渐增加，应力再次上升，说明部分原子重新回到平衡位置，形成新的有序晶格结构，这使得应力出现短暂的上升过程。这种现象与Koh 等人[24]的研究相吻合，说明该高熵合金具有较好的塑性。

2.3 温度对Al1.0CoCrFeNi 拉伸力学性能的影响

为了探究温度对Al1.0CoCrFeNi HEAs 拉伸性能的影响，改变拉伸加载时的模拟温度，采用了300 K 到1 500 K 等8 种不同的变形温度，设置同样的应变速率为1×1010s−1，对Al1.0CoCrFeNi HEAs 进行Y 轴单轴拉伸。图6（a）为不同温度下Al1.0CoCrFeNi HEAs 的应力-应变曲线，图6（b）为不同温度下Al1.0CoCrFeNi HEAs 的屈服强度曲线以及杨氏模量变化曲线，图6（c）为不同温度下Al1.0CoCrFeNi HEAs 的位错总长度变化曲线。

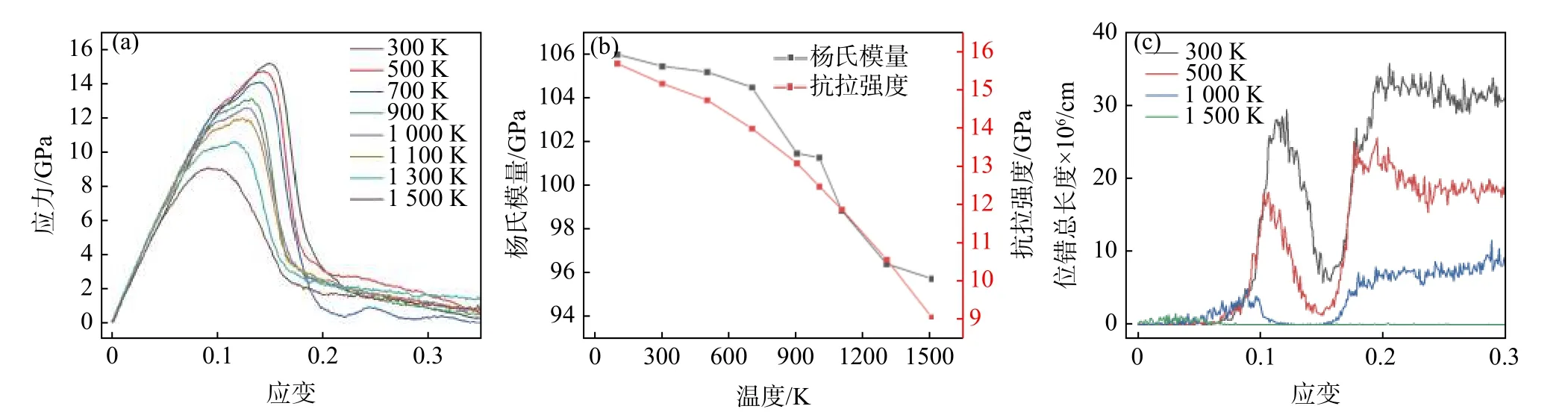
图6 不同温度下(a) Al1.0CoCrFeNi 应力-应变曲线,(b) 屈服应力曲线,(c) 位错总长度变化曲线Fig.6 (a) The stress-strain curve,(b) the Young’s modulus and the yield stress,(c) variation curve of total dislocation length of Al1.0CoCrFeNi at different temperatures

从图6（a）中可以看出，不同温度下，原子模型应力-应变曲线的变化趋势基本相似，但随着温度升高，屈服应力及对应屈服应变、杨氏模量逐渐降低，其量化结果见图6（b）。可以看出，杨氏模量从300 K 时的105.5 GPa 减小到1 500 K 时的95.8 GPa，减小了9.19%；屈服应力从15.17 GPa（300 K）降到9.12 GPa（1 500 K），降幅为39.88%，且绝对斜率增大。这一趋势很好理解，温度的升高导致原子热运动加剧，原子之间的键被破坏，晶体结构易变形，合金会“软化”，强度降低。从图6（c）可以看出，位错随着温度的升高逐渐减少，不同位错之间的相互作用减弱，无法形成固定位错阻碍材料运动，导致材料强度下降。

2.4 应变速率对Al1.0CoCrFeNi 拉伸力学性能的影响

为了研究高应变速率对拉伸变形机制的影响，对比了低应变速率 (≤1×109s−1)、中应变速率(1×109s−1<≤1×1010s−1)与高应变速率(>1×1010s−1)的不同影响，采用了从1×108s−1到2×1010s−1等6 种不同的应变速率，对Al1.0CoCrFeNi 在300 K 下进行Y方向单轴拉伸。图7（a）是不同应变速率下Al1.0CoCrFeNi HEAs 的应力-应变曲线，图7（b）是不同应变速率下Al1.0CoCrFeNi HEAs 的屈服应力曲线，图7（c）是不同应变速率下Al1.0CoCrFeNi HEAs的位错总长度变化曲线。

从图7（a）中可以看出，300 K 时初始弹性阶段，6 种不同应变速率的Al1.0CoCrFeNi 应力和应变曲线基本重合，均呈线性增加，说明初始弹性阶段对应变速率不敏感而进入屈服阶段后，屈服应力和应变随应变速率的增加而增加。在低应变速率和中应变速率(1×109s−1≤≤1×1010s−1)下，当应力达到抗拉强度后急剧下降；而高应变速率(>1×1010s−1)下，当应力达到抗拉强度后，应力-应变曲线下降相对缓慢，表现出较好的塑性。从图7（b）和7（c）中可以看出，材料在不同应变速率下均表现出屈服应力随应变速率增大而增大，表明应变速率对AlxCoCrFeNi 的屈服强度有明显影响。低应变速率的曲线斜率为1.02，中应变速率的曲线斜率为1.07，且中低应变速率拉伸初始阶段位错增长趋势基本重合，说明中低应变速率对材料在初始阶段拉伸无明显影响；当应变速率大于1010s−1时曲线斜率最大为2.36，即应变速率对材料的屈服应力及抗拉强度有明显影响，说明AlxCoCrFeNi 对高应变速率敏感。此外，当应变速率为1×109s−1时，位错总长度最大，说明高应变速率和低应变速率都不利于位错的生成。

图7 不同应变速率下(a) Al1.0CoCrFeNi 的应力-应变曲线,(b) 屈服应力曲线,(c) 位错总长度变化曲线Fig.7 (a) The stress-strain curves，(b) the yield stress,(c) variation curve of total dislocation length of Al1.0CoCrFeNi at different strain rates

3 结论

基于分子动力学，建立单轴拉伸模型，研究了常温和常规应变速率下AlxCoCrFeNi HEAs 不同Al含量对其力学性能的影响，Al1.0CoCrFeNi HEAs 在高温和高应变速率下的力学行为和变形机理，对Al1.0CoCrFeNi HEAs 在单轴拉伸过程中的力学行为以及不同因素对Al1.0CoCrFeNi HEAs 拉伸力学性能的影响进行了研究，包括Al 含量（x=0.1，0.3，0.5，0.7，1.0），不同的拉伸速率（108～2×1010s-1），不同的温度（300～1 500 K），得到如下结论:

1）在常温（300 K）条件下，分析径向分布函数RDF 以及不同晶格原子数量变化，证实了随着应变的增加，Al1.0CoCrFeNi HEAs 由原来单一的BCC 结构向FCC、HCP 和Other 原子相变，这表明高熵合金的塑性变形与材料的相变有关。

2）常温（300 K）和中应变速率（1010s−1）下，Al 摩尔比0.1 至1.0 时，AlxCoCrFeNi HEAs 屈服应力随Al 含量上升呈下降趋势。随着Al 含量的增加，会导致HEAs 更容易发生变形，更早进入屈服阶段，力学性能降低。

3）在300～1 500 K 条件下，Al1.0CoCrFeNi HEAs的屈服应力同样随温度的升高呈下降趋势。其内部原因位错随着温度的升高逐渐减少，不同位错之间的相互作用减弱，无法形成固定位错阻碍材料运动，导致材料强度下降。

4）常温（300 K）环境下，应变速率对Al1.0CoCrFeNi 屈服应力和抗拉强度有明显影响，高应变速率（应变速率大于1×1010s−1）时屈服应力和抗拉强度明显增大，说明Al1.0CoCrFeNi HEAs 具有高应变速率敏感性。此外，高应变速率和低应变速率都不利于位错的生成。