线性求解器在中长期水量调度中的应用研究

赵亚威，方洪斌

（1.黄河勘测规划设计研究院有限公司，河南 郑州 450003；2.水利部黄河流域水治理与水安全重点实验室（筹），河南 郑州 450003）

1 引 言

中长期水量调度是在中长期时间尺度下（年计划月调度或月计划日调度），协调当地地表水、地下水、非常规水、外调水等多个水源供水量和用户需水量的一项水资源优化配置工作，是实现水资源系统水量供需平衡和水资源系统综合效益最大化的重要手段。随着用水结构、供水来源的多样化发展，区域水资源系统的复杂性不断提升，使得中长期水量调度模型变量和约束增多、规模变大，求解难度随之增加，寻求快速、精确的模型求解方法成为目前中长期水量调度的重要研究方向之一。

国内外许多学者对中长期水量调度模型求解算法进行了研究，主要分为模拟算法和优化算法。模拟算法［1－4］是一种经验方法，主要依靠调度经验将模型的一些复杂约束条件概化为对应的调度规则，进而降低模型的求解难度，实际应用较为广泛，然而这种方法缺乏最优化理论支撑，获取的解往往不是最优解；优化算法种类较多，主要分为以线性规划、动态规划等为代表的传统优化算法［5－8］和以遗传算法、粒子群算法等为代表的智能优化算法［9－10］。传统优化算法比智能优化算法求解效率低，例如线性规划在求解大规模复杂模型时计算量较大、计算时间较长，但线性规划全局寻优的优良特性驱使国内外学者对提升其求解效率的研究不断深入。随着计算机硬件和软件技术的不断突破，计算机整体性能逐步提升，并行计算成为加速线性规划计算效率的重要方式，例如目前比较流行的CPU并行、GPU并行可以实现多核、多线程并行计算，能够大幅提升计算效率。针对线性规划求解效率低的问题，许多学者和软件厂商基于并行技术开发了线性规划软件。线性求解器是专门用于求解线性规划问题的软件或程序集（大部分求解器还可求解非线性规划问题，如二次规划），目前国际上流行的线性求解器主要有Cplex、Gurobi、Xpress、Lingo／Lindo等，免费开源求解器主要有Lpsolver、Scip、Glpk、Matlab等；国内线性求解器发展起步较晚，目前应用较为广泛的主要有Cmip、Leaves等。经过大量实例验证，线性求解器在求解大规模复杂线性模型时显现出优秀的计算性能。

本文将线性求解器运用于中长期水量调度模型求解中，并将其与遗传算法进行对比，以期探索模型的快速求解技术，为中长期水量调度方案编制提供参考。

2 中长期水量调度模型

2.1 水资源系统网络拓扑

中长期水量调度模型一般基于网络拓扑构建，网络拓扑由节点、连线构成，节点表示输入水量、输出水量、蓄水量等，连线表示水流方向。对于水资源系统，节点可对应水库、配水枢纽、控制断面、水厂、用水户等，其中水库有蓄水库容、配水枢纽有调节池，均具有一定调蓄能力，故蓄水量可变化；连线可对应河流、渠道、隧洞、管线等，在进行中长期水量调度时，一般将连线蓄水量设为恒定值或0。节点和连线遵循水量平衡原则，构成供需水网络。节点、连线水量平衡示意图分别见图1、图2。图1中，R上游、R区间、R退水、R地表、R地下、R其他分别为节点i的上游相邻节点出流水量、区间水量、退水量、当地地表水量、地下水量、其他水量（再生水、收集雨水、淡化水等），均为节点i的输入水量；C下游、C退水、C损失、C生活、C工业、C农业、C生态分别为节点i的下游相邻节点入流水量、退水量、损失水量、生活供水量、工业供水量、农业供水量、生态供水量，均为节点i的输出水量；S时段初、S时段末分别为节点i时段初、末蓄水量。图2中，R节点i为连线ij上游节点i的出流水量（输入水量）；C损失、C节点j分别为连线ij的损失水量、下游节点j的入流水量（输出水量）；连线ij的箭头表示水流方向。

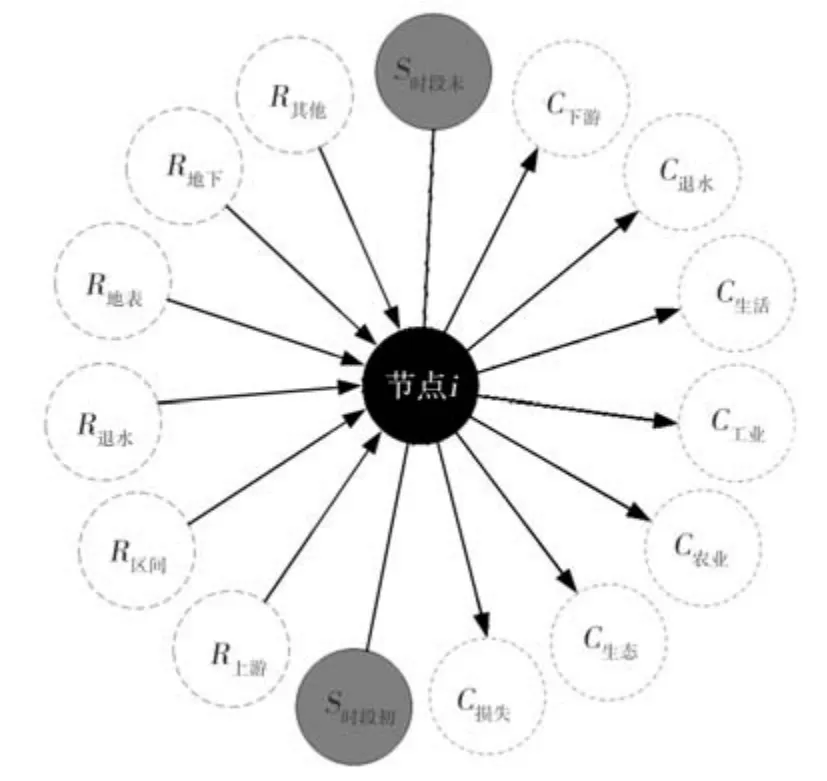
图1 节点水量平衡示意

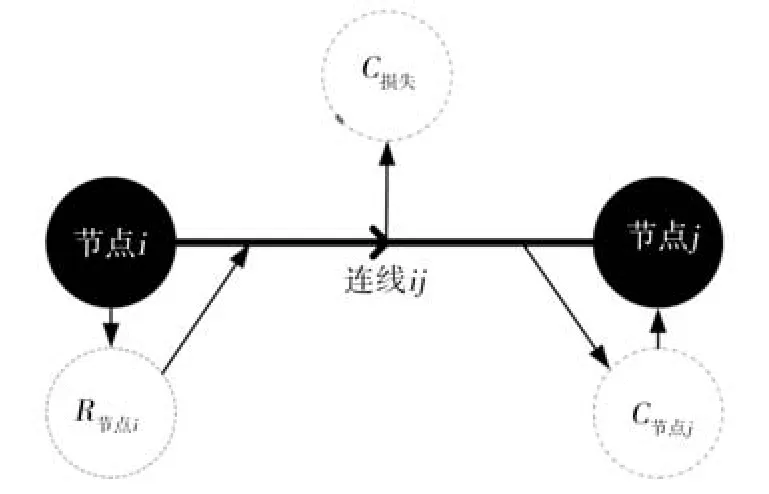
图2 连线水量平衡示意

2.2 基于网络拓扑的水量调度模型

网络拓扑是描述水资源系统各单元水量供需关系的重要工具，依据网络拓扑节点和连线的上下游关系、水量平衡约束、其他约束条件以及调度目标可构建中长期水量调度模型。

2.2.1 目标函数

以水资源系统总缺水量最小为优化目标，目标函数表达式为

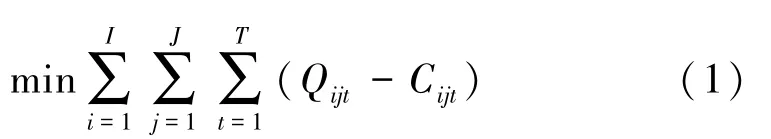
式中：I为节点总数；J、j为节点上用水户总数、序号，j取值为1、2、3、4，分别表示生活、工业、农业、生态用水户；T为调度时段总数；Qijt、Cijt分别为节点i用户j时段t的需水量和实际供水量。

2.2.2 约束条件

（1）节点水量平衡。表达式为

其中

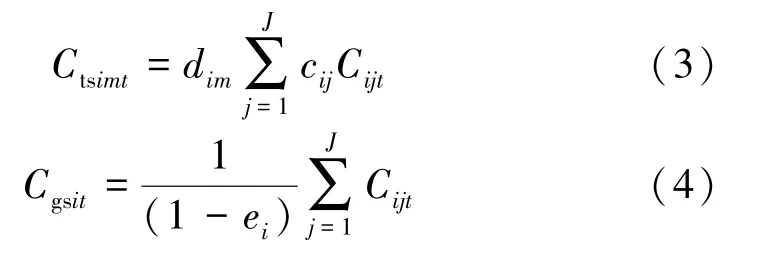
式中：Ni、n分别为节点i上游相邻节点总数、序号；Mi、m分别为节点i下游相邻节点总数、序号；Rsyint、Rqint、Rtsint及ain、bin、fin分别为节点i时段t的上游第n个相邻节点出流水量、区间入流水量、退水量及对应的沿程损耗系数；Cxyimt、Ctsimt、Cgsit、Cdcit分别为节点i时段t的下游第m个相邻节点出流水量、退水量、总供水量、调出到外系统水量；Vi（t－1）、Vit分别为节点i时段t初、末蓄水量；cij为节点i用户j的退水系数；dim为节点i与下游相邻节点m之间的退水量占节点i总退水量的比例；ei为节点i上供水管网损耗系数；K、k分别为节点上水源数量、序号，其中k取值为1、2、3、4，分别表示当地地表水、地下水、非常规水和过境水（上游相邻节点出流水量、区间水量、退水量之和）；Dijkt为时段t水源k向节点i用户j的实际供水量。

（2）连线水量平衡。若网络拓扑中节点i与节点p直接相连，水流由节点i流向节点p，则连线ip满足如下水量平衡方程：

式中：Cxyivt为时段t从节点i流向节点p的出流水量；Rsyput为时段t由节点i流入节点p的水量；v为节点p在节点i下游相邻节点中的序号，1≤v≤Mi；u为节点i在节点p上游相邻节点中的序号，1≤u≤Ni。

（3）节点出流上限、下限约束。约束条件为

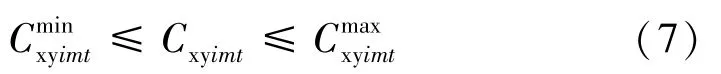
式中：、分别为节点i下游相邻的第m个节点时段t的出流量下限、上限，为节点的过流能力，一般取0，若当前节点存在生态流量约束，则取生态流量。

（4）节点蓄水量上限、下限约束。约束条件为

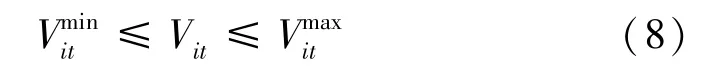
（5）节点各水源向各用户的实际供水量上限、下限约束。约束条件为

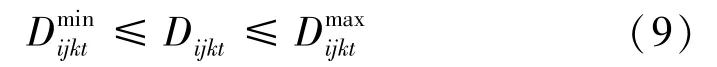
式中：、分别为时段t节点i上水源k向用户j的实际供水量下限、上限。

3 基于线性求解器的模型求解

本文所构建的中长期水量调度模型中不含非线性表达式，为标准的线性规划模型，可采用线性求解器进行求解。线性求解器的种类较多，但主要的数学原理、求解方法、操作流程有相似之处。数学原理方面，大多数求解器是基于单纯形法、分支定界法等传统的线性规划方法；求解方法方面，大多数求解器是输入标准化线性规划模型的目标函数系数向量、约束条件系数矩阵和常数向量、目标优化方式Max／Min、决策变量个数、整数变量个数等信息，然后进行求解，最后得到最优决策向量和目标值；操作流程方面，使用线性求解器求解模型一般需要编写程序，主要有集成开发环境（IDE）和基于应用程序编程接口（API）两种方式。IDE的优点是程序编写方式与数学模型的书写习惯较为统一，程序结构简单；缺点是不同求解器的程序语法往往不同，在使用多种求解器时需要熟悉多种IDE程序语法，另外IDE一般不能与其他语言进行程序混编，无法集成到C／C＋＋、Java、Python等其他应用程序开发系统中。API优点是支持C／C＋＋、Java、Python等当前主流编程语言，程序语法易于学习，调用方便，便于进行多语言混编，可用于大型应用系统的优化计算和模块开发；缺点是很多求解器不提供API，有的仅支持部分主流编程语言，且API功能相较于IDE相对单薄。

本文采用C＃与Cplex、Lpsolver线性求解器API混合编程实现模型求解，步骤如下。

（1）模型前处理。将模型进行标准化处理，包括将目标函数转化为“Min”形式以及将所有不等式约束条件转化为“≤”形式。

（2）模型关键参数提取。提取中长期水量调度数学模型中的关键信息，包括目标函数中决策变量系数向量C、约束条件中决策变量系数矩阵A和常数向量b、决策变量上下限、决策变量为整数或非整数等信息，形成矩阵数据或向量数据。

（3）模型求解。将步骤（2）提取的所有数学模型矩阵数据和向量数据，整理成Cplex或Lpsolver的API标准化输入形式，调用求解器中的线性规划方法对模型进行求解。

（4）结果输出。按照Cplex或Lpsolver输出的规则，将计算得到的最优结果解析为方便进行方案分析的数据格式。

小儿柴桂退热颗粒的UPLC指纹图谱及聚类、主成分分析…………………………………………………… 林 源等（4）：474

4 实例分析

以北方某城市2025年规划水平年中长期水量调度为例进行分析。该市境内主要河流有5条，分别命名为河流A、B、C、D、E。该市现状供水水源主要由当地地表水、地下水、非常规水和从A河引水组成。2019年该市从A河引水量8.7亿m3，占该市总用水量的38.3%。从A河引水进入该市水资源系统后，主要由位于河流B的水库1和位于河流D的水库2进行调节，供给该市生活、工业、农业、生态环境需水。该市水资源系统概化见图3，网络拓扑概化见图4。采用Cplex、Lpsolver、GA（遗传算法）对模型进行求解。

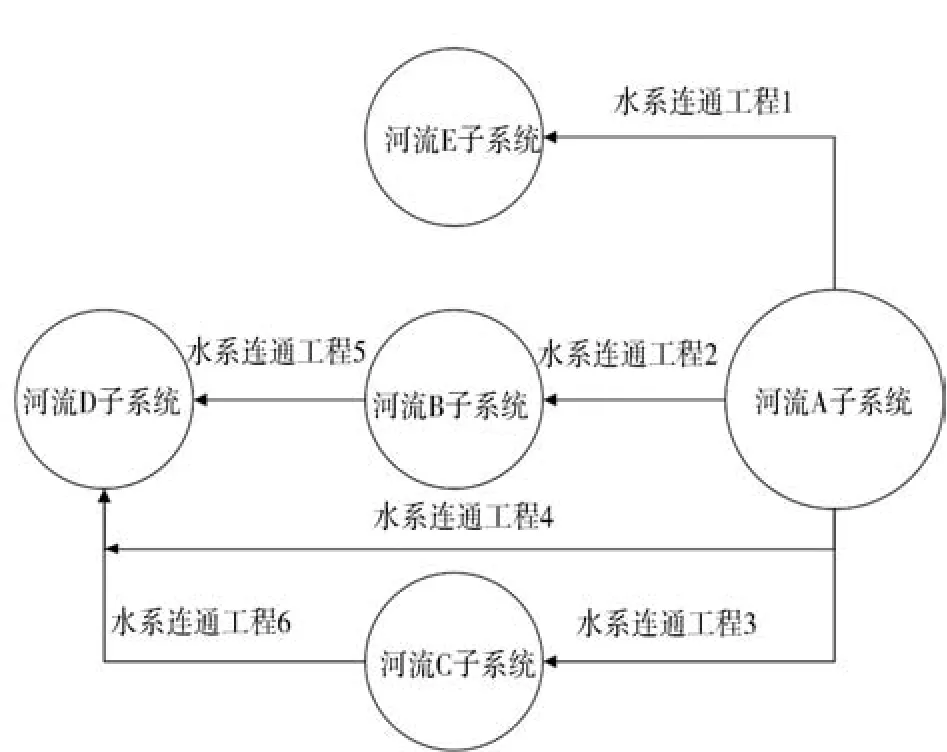
图3 某北方城市水资源系统概化

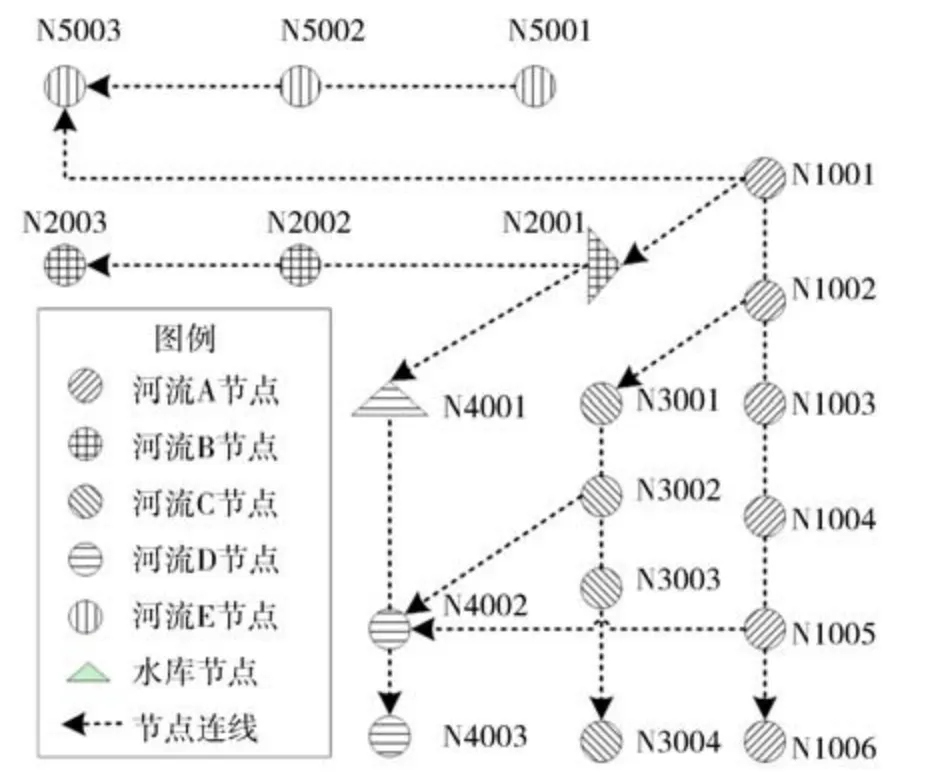
图4 某北方城市水资源系统网络拓扑概化

4.1 不同方案优化结果分析

该市每年各月按照一定比例（见表1）从河流A的控制水库引水，按照河流A来水量丰枯变化，分别设置从A河年引水量4亿、5亿、6亿、7亿、8亿m35种方案，优化结果见表2。

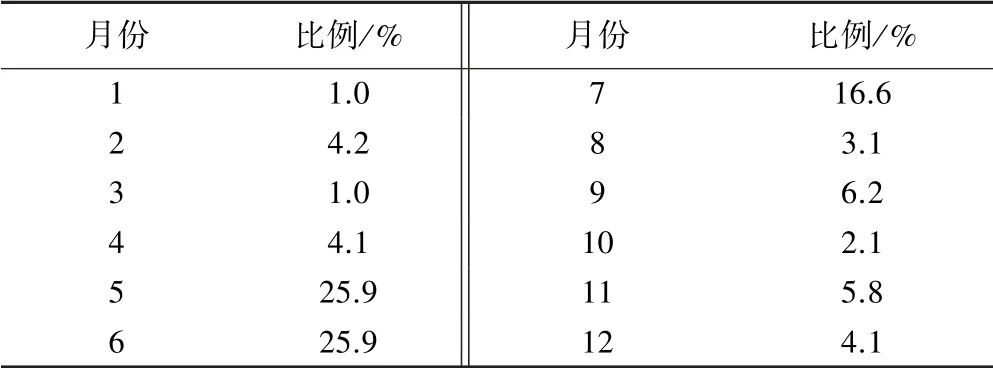
表1 某北方城市各月从河流A的引水量比例

表2 从A河引水不同方案优化结果

从优化结果来看，各方案Cplex、Lpsolver优化得到的缺水量和缺水率均小于GA的优化结果，原因是Cplex、Lpsolver是基于线性规划的全局优化算法，而GA则存在易陷入局部最优的缺点，无法保证收敛到全局最优解。从计算时间来看，采用Cplex、Lpsolver的各方案计算时间均小于0.1 s，而采用GA的计算时间最短需978.89 s，最长则需1 188.83 s，Cplex、Lpsolver计算时间远远少于GA，原因是Cplex、Lpsolver采用了并行计算，充分发挥了计算机性能，极大提升了计算效率，而GA不仅存在繁琐的选择、交叉、变异和迭代等过程，且未采用并行计算，计算效率较低。

4.2 不同规模模型优化结果分析

为了进一步检验不同算法的性能，改变模型规模进行对比分析。以图4模型19个节点（大规模）为基础，将节点数精简为8个（小规模），分别采用Cplex、Lpsolver、GA进行优化求解，结果见表3。

表3 小规模模型从A河引水不同方案优化结果

通过对比表2、表3可知，由于Cplex、Lpsolver求解效率较高，因此模型规模大小对其计算时间影响不大；小规模模型和大规模模型不同A河引水方案下，GA的平均计算时长分别为111.70、1 107.84 s，GA限于自身算法的复杂性和未采用并行机制，随着模型规模的增大，计算时间增加。

4.3 从A河引水时机分析

由表2、表3可知，从A河引水8亿m3时，仍不能满足总水量需求，原因是各月从A河引水比例与该市需水比例变化趋势不完全一致，而该市境内主要依靠水库1、水库2来调节从A河引水分配过程，这两座水库兴利库容分别为0.651亿m3和0.684亿m3，相较于从A河引水量4亿～8亿m3来说均很小，调蓄能力非常有限，无法进行时空调节。为解决这一问题，可以从增加水库兴利库容或者改变引水时机两方面入手，但该市近期没有新建水库或增加现有水库兴利库容的规划，因此只能从改变引水时机角度考虑改善缺水状况。

在实际调度中，该市年内各月从A河的引水量为固定值，可表示为

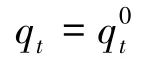
式中：qt、q0t分别为第t月该市从A河的引水量、固定引水量。

对原模型进行改进，将“各月从A河引水量为固定值”等式约束修改为“各月从A河引水量之和为固定值”等式约束，计算公式为

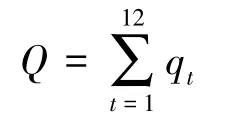
式中：Q为从A河年引水总量。Q与q0t的关系为

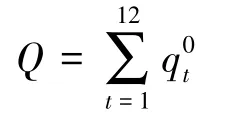
以16个节点模型为例，以从A河引水量4亿m3为起点、8亿m3为终点，等值离散为若干个方案，采用Cplex算法对不同引水量下不考虑引水时机（原模型）和考虑引水时机（改进模型）两种模型进行求解，得到从A河引水量与缺水量的关系，见图5。

图5 从A河引水量与缺水量的关系

（1）不同引水方案下，改进模型的缺水量均小于原模型，且随着从A河引水量的增加，改进模型较原模型缺水量逐渐减小，说明改变引水时机能够减小从A河引水量，节约系统供水成本。

（2）当从A河引水量为7.65亿m3时，改进模型的缺水量为0，该引水量下水库1、水库2的水位变化过程见图6和图7，可以看出，原模型水库1仅在2月、9月发挥了调蓄作用，水库2仅在5月、8月、9月发挥了调蓄作用，而改进模型的水库1和水库2的蓄泄变化过程更加明显，说明改进模型充分发挥了水库的调蓄作用。原模型、改进模型从A河引水过程见图8，可知：7月、9—12月当地水量较富裕，改进模型比原模型减小了引水量，而在1—4月、6月加大了从A河引水量，弥补需水缺口；5月需水量较大，而改进模型从A河引水量小于原模型，原因是改进模型1—4月从A河引水量较大，增加了水库1、水库2的蓄水量（5月初水库1、水库2蓄水量较大），5月从A河引水，水库1和水库2同时向用户供水，故改进模型5月从A河引水量小于原模型；8月当地水量非常富裕，原模型从A河引水量较小，而改进模型引水量较大，原因是8月当地水主要来自节点N1002、N1004、N1006、N2001、N2002、N3002、N4001、N5002、N5003，除N2001（水 库1）、N4001（水库2）外，其他节点当地水量（为3.35亿m3，占8月当地水总量的92.76%）均无法存入水库1和水库2，不能被调蓄，因此需要加大从A河引水量，来满足9—12月用户需求。从图6、图7可以看出，8月末水库1和水库2蓄水量明显增加，且9—12月为开闸供水状态，水库水位不断降低，直至水库放空。综上所述，与原模型相比，改进模型充分发挥了当地水库的调蓄作用。

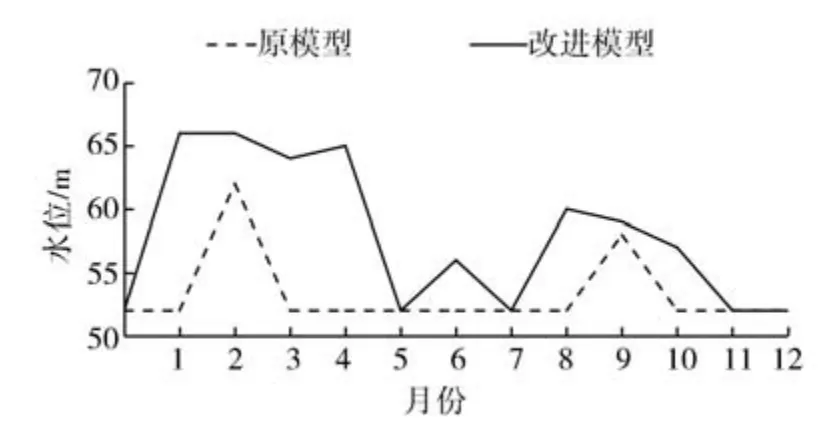
图6 水库1水位变化过程

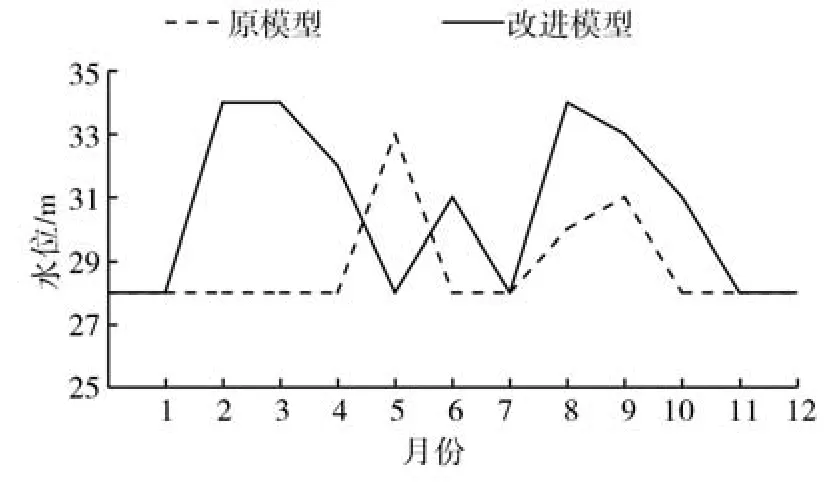
图7 水库2水位变化过程

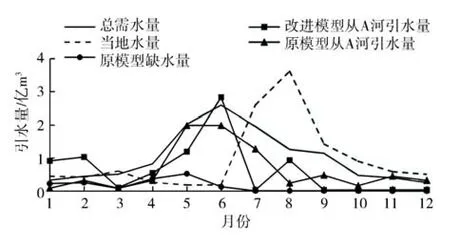
图8 原模型、改进模型从A河引水过程

5 结 语

本文以北方某城市水资源系统为例，建立中长期水量调度模型，采用线性求解器对模型进行求解，并与遗传算法进行了对比。主要结论如下：①线性求解器Cplex、Lpsolver编程简单，能够获得全局最优解，求解精度高、速度快；②当模型规模增大时，遗传算法计算效率明显下降，而Cplex、Lpsolver计算效率变化不明显；③通过改变引水时机能够充分发挥现有水库的调蓄能力，增加系统总供水量。

线性求解器应用的前提是模型必须为线性模型，因此如何实现含非线性约束的中长期水量调度模型的线性化处理，是下一步的研究重点。