NSGA-II应用于圆筒型永磁直线电机的多目标优化＊

彭 珍，刘春元，饶章宇，李广力

(1.浙江理工大学信息学院，浙江 杭州 310018；2.嘉兴学院信息科学与工程学院)

0 引言

圆筒型永磁直线电机(TubularPermanent Magnet Linear Motor,TPMLM)具有推力密度高、伺服特性优良、加工装配容易、气隙磁场高且不存在横向端部效应等特点，广泛应用于海浪发电[1]、振荡系统[2]以及高精度数控机床[3]等工业领域，研究高效可靠的圆筒型永磁直线电机具有重要意义。

目前，电机优化设计的主要目标是提高推力密度[4]，减少推力脉动[5]等。近年来，提出了很多相关的优化方法，其中最为主要的优化方法是结构优化[6]和算法优化[7]。而其中的多目标优化是算法优化中最为方便和高效的方法之一。

对于算法的优化，文献[8]为了防止算法“早熟”，提出了带黑洞机制和混沌搜索的多目标粒子群优化算法，达到了增加种群的多样性、提高算法寻优精度的效果。文献[9]为了同时实现新型轴向磁场永磁记忆电机的高性能和低成本，提出一种结合分层优化策略的响应曲面法(Response surface method,RSM)和基于罚函数与目标约束的NSGA-II-M 多目标优化设计方法，并得出NSGA-II-M 在求解此类多目标优化问题上比RSM 更具优势，同时也证明了NSGA-II 的有效性。因此，本文针对现有电机优化中存在的优化效率低、优化效果不理想等问题，提出使用基于NDX算子的NSGA-Ⅱ对电机的功率和效率进行多目标优化，以期实现电机的功率和效率的提升。

首先，搭建二维仿真模型，根据TPMLM 的尺寸在ANASYS Maxwell 上建立二维模型；其次，数据分析，计算优化前电机的功率和效率，利用敏感参数分析法获取主要影响变量；然后，多目标优化，利用基于NDX算子的NSGA-Ⅱ对功率和效率进行优化，获得Pareto前沿和优化后的目标值和变量值；最后再与优化前的数据进行对比，并使用样机验证。

1 圆筒型永磁直线电机多目标优化模型

1.1 目标函数

本文选取功率最大和效率最高作为电机设计的优化指标，在TPMLM 电机的多目标优化敏感性优化分析中，目标函数如式⑴、式⑵所示：

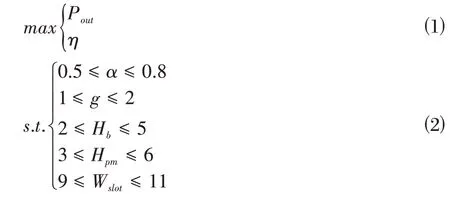
其中，Pout为电机的输出功率，η为电机运行时的输出功率与输出功率、磁滞损耗和绕组损耗之和的比值。输出功率Pout和运行效率η的计算如式⑶、式⑷所示：

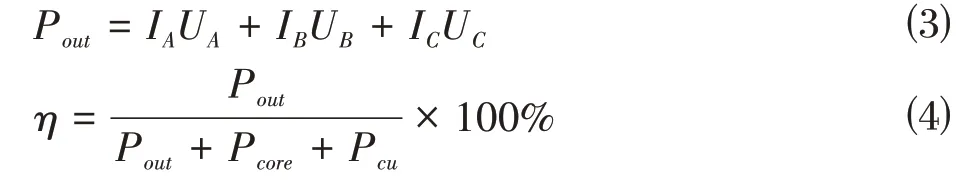
其中，IA、IB、IC、UA、UB和UC为分别为内部电路中三相电路各相电路的电流与电压值；Pcore为磁滞损耗，磁滞损耗的数据由仿真模型导出；Pcu为绕组损耗，绕组损耗的计算如式⑸所示：

其中，R是三相电路上各相的绕组电阻，取阻值10Ω进行计算。

1.2 优化变量

本文所研究的TPMLM 的初始结构参数数据如表1所示。

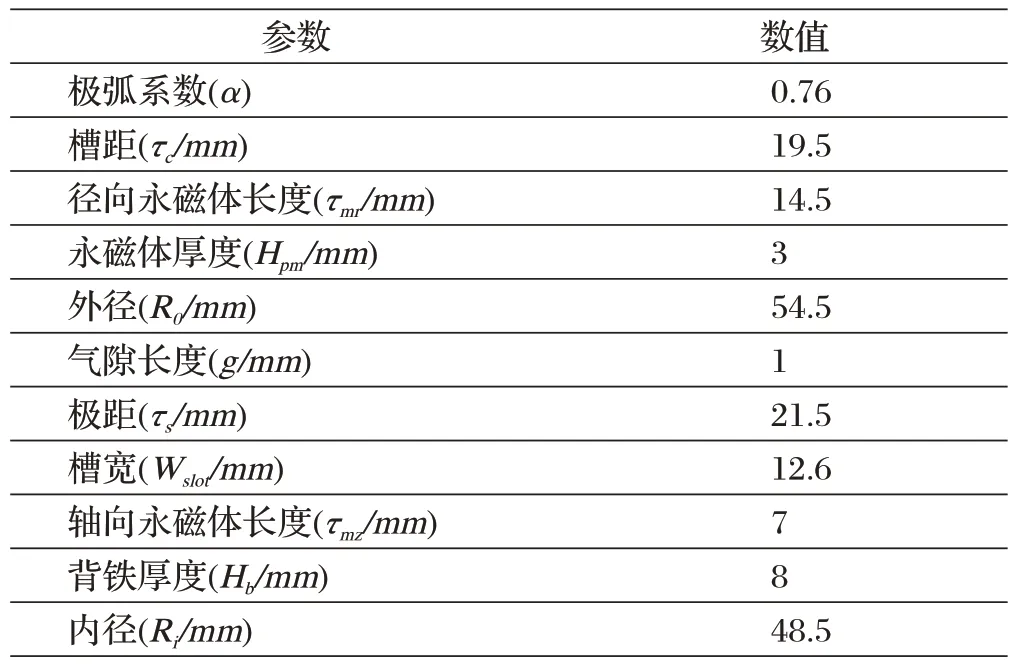
表1 电机设计主要参数数据

根据灵敏度分析[10]，从表1 中的所有参数数据中选取了五个关键结构参数作为TPMLM 的优化变量。根据输出性能随参数变化进一步给出每个参数变量的限制范围，如表2所示。

表2 优化变量及参数范围

1.3 优化设计流程图

本文整体的优化设计过程如下：首先，确定优化目标和设计变量以及变量的取值范围。其次，计算和分析设计变量对优化目标的敏感性指数，利用灵敏参数分析法选取灵敏度高的参数。然后，再利用基于NSGA-II的多目标优化算法生成优化目标的Pareto前沿。最后，确定设计变量的最佳值，通过仿真和实验验证电机的功率和效率的性能。具体如图1所示。

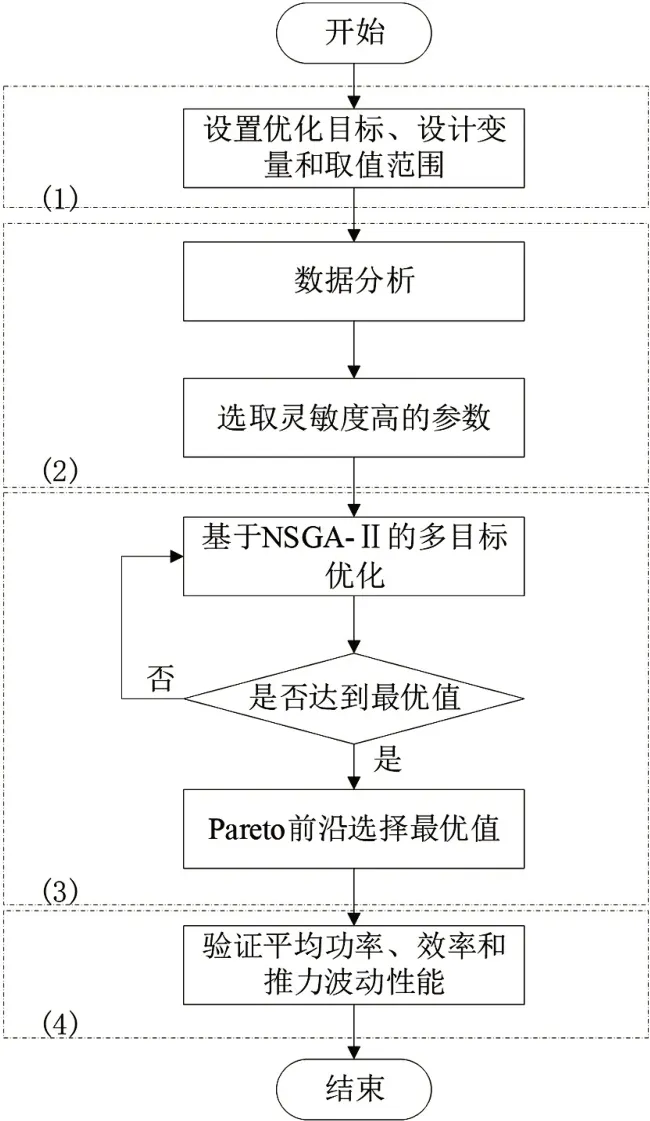
图1 多目标优化设计流程图

2 基于NDX算子的NSGA-Ⅱ多目标优化

2.1 NSGA-II的特点

近年来，多目标优化中采用了多种多目标进化算法，如多目标粒子群优化(MOPSO)、多目标差分进化(MODE)和多目标遗传算法(MOGA)。为了获得具有最优参数设计的良好优化方法，在[11]中，对多目标粒子群优化算法(MOPSO)、多目标差分进化算法(MODE)和非支配排序遗传算法(NSGA-Ⅱ)三种进化算法进行了性能评估。评估结果表明：MODE 存在过早收敛的问题，而MOPSO 容易陷入局部最优解，相比之下，MOGA 具有较强的全局搜索能力，但不能保证搜索的多样性，收敛速度较慢，结果表明了NSGA-II提供了更好的最优解，因此，本文使用NSGA-II 进行多目标优化。

NSGA-Ⅱ由Deb[12]等人首次提出，其主要思想为带有精英保留策略的快速非支配多目标优化算法，是一种基于Pareto 最优解的多目标优化算法。NSGA-Ⅱ在执行选择、交叉和变异遗传操作之前，会对个体先进行分层排序，确定种群间的支配与非支配关系，同时，提出个体的拥挤度和精英策略来保证种群的多样性，并降低了计算复杂度并尽可能保留满意解。

NSGA-II 的实数编码所采用的交叉算子为模拟二进制交叉(simulated binary crossover)算子，简称SBX 算子，定义为：对两个父体x1和x2，按照以下方式生成两个子个体c1和c2：

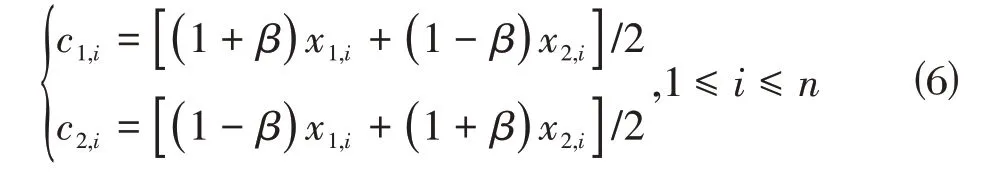
其中，β为随机变量，在每一维上都需要重新生成，以第i维为例(设x1,i≥x2,i)，可以将式⑹变换为如下形式：

(x1,i+x2,i)/2 表示两个父体在第i 维上的中点，将(x1,i-x2,i)/2视为该维上的搜索步长。

基于SBX算子的NSGA-Ⅱ中的β为随机变量，其搜索范围有限，易出现局部最优和进化过程不稳定等问题。

2.2 基于NDX算子的NSGA-Ⅱ

针对SBX 算子的不足，将正态分布引入到交叉操作SBX中，即用1.481|N(0,1)|代替参数β来扩大搜索空间，增强的空间搜索能力，N(0,1)为正态分布随机变量。故式⑺可表示为：

基于NDX 算子的NSGA-Ⅱ在Pareto 前沿的完整性、均匀分布性、算法收敛性上都有显著改善，更容易跳出局部最优，提高Pareto最优解的质量，并将此算法用于圆筒型永磁直线电机的多目标优化中，不仅能获得更多具有代表性的非劣解，而且有利于其做出更合理的决策。改进后的NSGA-II的流程图如图2所示。

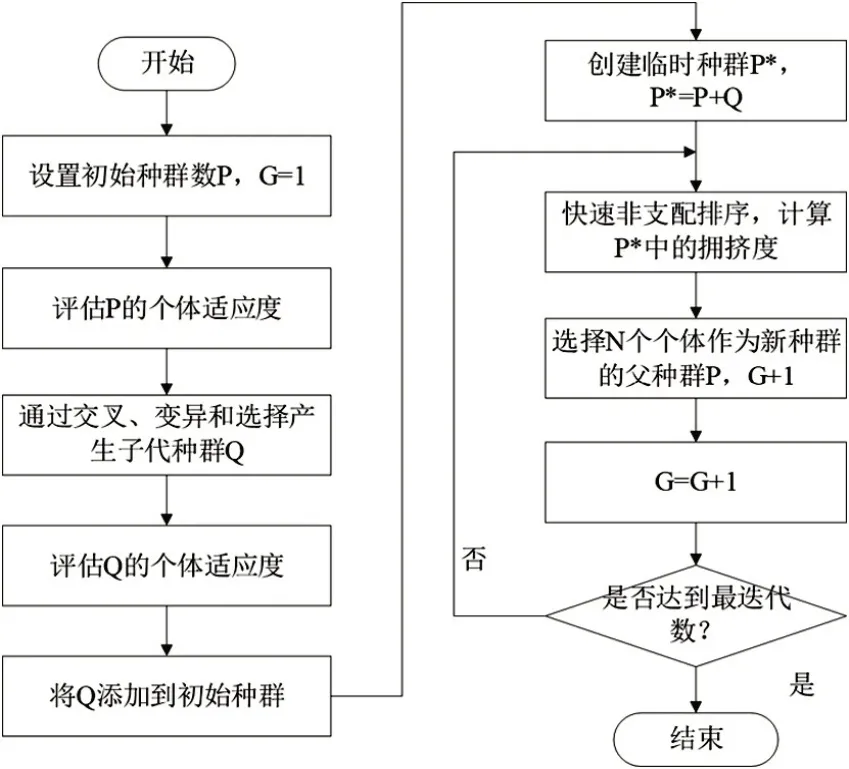
图2 NSGA-II流程图

3 性能对比

所采用的基于NDX 算子的NSGA-Ⅱ的参数设置如下：种群规模大小设置为300；变异算子的变异概率设置为0.2；交叉算子的交叉概率设置为0.8；最大迭代次数设置为1000。优化后的Pareto 前沿如图3 所示，优化前后设计变量的取值如表3所示。

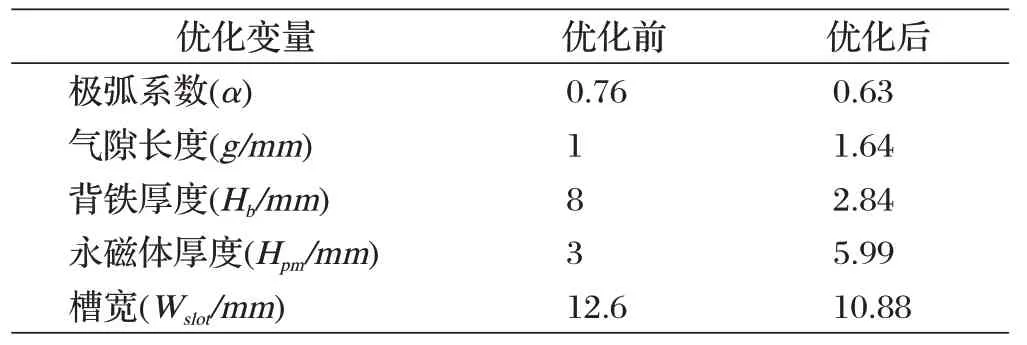
表3 优化前后的设计变量值

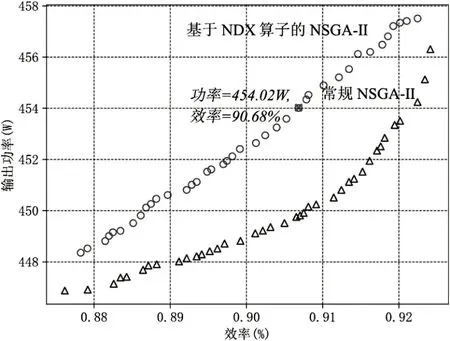
图3 Pareto前沿

从图3 可得：由于基于NDX 算子的NSGA-Ⅱ搜索空间更为广阔，使得Pareto最优解分布均匀，而且解的质量要更高。通过优化，功率由401.52W提高到了454.02W，效率从82.83%增大到了90.18%。

3.1 功率性能

在速度为0.5m/s，负载为10Ω时计算瞬时功率，优化前后瞬时功率的结果如图4所示，从图中可以看出，优化后的TPMLM的功率得到了增大，TPMLM的平均功率由优化前的401.52W变为优化后的454.02W，达到了优化效果。

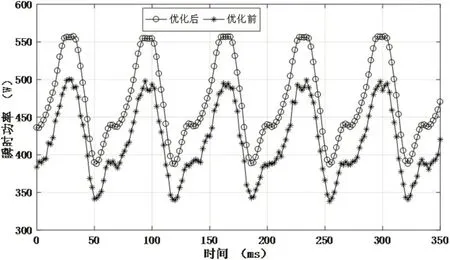
图4 功率的优化结果

3.2 效率性能

TPMLM 的绕组的电阻取值为0.8Ω，在速度为0.1-1.0m/s时分别计算运行效率，结果如图5 所示，从图中可以看出，优化后的电机的工作效率相比优化前，有明显的提升，电机平均效率由优化前的82.83%变为优化后的90.18%，达到了优化效果。

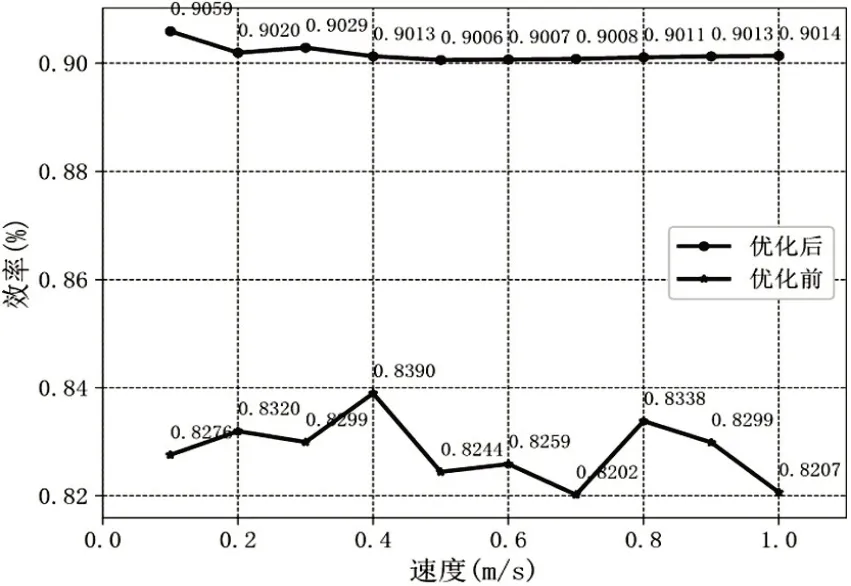
图5 效率优化对比

4 实验

为了验证所设计的永磁直线电机能应用于桥梁的减振系统，使用MTS100kN 万能试验机模拟桥梁的振动。实验平台的搭建如图6所示。

图6 实验平台

在电机的运动速度为0.112m/s，负载R=5Ω的工作条件下，用示波器测量感应电动势，用MTS100kN万能试验机读取电磁力，即阻尼力。图7(a)所示为测量的A相感应电动势，(b)为仿真的三相感应电动势波形。从图中可看出，其感应电动势幅值测量值为15V，有限元计算值为15.4V，仿真计算值和实验测试值基本一致。

图7 感应电动势

5 结束语

本文提出了一种基于NDX 算子的NSGA-Ⅱ的TPMLM 的多目标优化设计方法。以效率和功率为优化目标。

本研究充分利用NSGA-II的全局收索能力对目标进行优化，通过动态拥挤度以及自适应混合交叉算子保证解的多样性，提高解的质量；通过全局优化，获得电机结构参数最优解，实现TPMLM的最佳运行性能。

样机的仿真和试验结果表明：通过电机参数结构的优化，在不同状况下，优化后功率提高，效率提升，而且样机实测表明该方法对TPMLM 结构优化设计的有效性。因此，所提出的TPMLM 优化设计可以方便、高效地获得最优结构设计。