高速滑动电接触电枢表面动态磨损过程研究
2023-01-30鲁军勇张永胜蔡喜元
李 白 鲁军勇 谭 赛 张永胜 蔡喜元
高速滑动电接触电枢表面动态磨损过程研究
李 白 鲁军勇 谭 赛 张永胜 蔡喜元
(海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430074)
电枢是电磁发射装置的关键部件,其表面磨损是引起发射过程中转捩的原因之一,同时磨损也会严重削弱电枢本体的力学性能,影响发射安全性,因此有必要对高速滑动电接触电枢表面的动态磨损过程进行深入分析。首先,分析电枢表面产生磨损的机理,厘清相关耦合因素;其次,考虑表面磨损量变化、温度升高及电枢尾翼向外扩张过程中反向受力的影响,建立电枢尾翼磨损量的理论计算模型,研究其磨损规律;最后,考虑电磁场-温度场-应力场-磨损等耦合因素建立三维有限元计算模型,对电枢尾翼磨损量进行更为准确的分析。结果表明:①电枢表面磨损量是在电因素及力因素的共同作用下产生的;②考虑了表面磨损量变化、温度及电枢尾翼向外扩张过程中反向受力等因素影响后,分析得到电枢表面磨损量较不考虑时小19.5%,但考虑后与实测值更为接近,证明了分析过程中上述影响因素不可忽略;③相比理论分析模型中对电枢尾翼法向力分量及反向受力的近似计算方法,有限元模型更为精确,其计算得到电枢尾翼磨损量与实测值也更为接近,验证了所建立模型的准确性。该文所建立模型及分析结果对于后续优化电枢结构、提高枢轨接触性能及保证发射安全性具有重要意义。
电磁发射装置 电枢 滑动电接触 表面磨损 多物理场耦合
0 引言
电枢是电磁发射装置的关键部件,对炮口处电枢进行实测的结果表明,在动态发射过程中其表面会产生严重磨损。磨损会带来以下两个方面的问题:①电枢磨损融化后会在内膛形成积铝层,附着在轨道表面,增大表面粗糙度,影响后续发射过程中枢轨间的接触状态;②尾翼磨损后,电枢所能够承受的力学性能被极大削弱,影响发射安全性。因此,对高速滑动电接触过程中电枢表面动态磨损过程进行分析,对于控制其表面磨损量、优化电枢结构、改善枢轨接触性能,具有重要意义。
针对电枢表面磨损过程,文献[1-2]基于固体接触面导热原理,建立了电枢和导轨接触面温度分布方程和电枢平均磨损量的计算方法,分析了驱动电流、电枢和导轨材料性能、接触参数对平均磨损率的影响,采用解析法对电枢磨损量进行分析,计算效率高,但仅考虑了理想及简化的模型,与实际工况相差较远,此外也没有考虑温度、磨损量与接触力间的耦合迭代关系,计算准确性难以保证;美国德克萨斯大学先进技术研究所(IAT)考虑实际装置,基于Ansys进行二次开发,建立了可以耦合考虑电磁、热、结构和磨损的二维及三维有限元分析模型[3-4],可以适用于复杂工况,但是模型非常复杂、工作量大、计算效率较低,且由于保密因素,现有公开文献无法获取其计算代码。另一方面,为便于对电枢磨损量及磨损过程进行准确观察,国内外学者也设计了相关试验进行研究。华中科技大学在电枢尾翼两侧设计了凸台结构,通过动态发射试验确定了电枢尾翼磨损率、枢轨接触电阻及摩擦系数,其试验方法及分析结果具有参考意义[5];IAT则在电枢表面埋入钨针,采用X光进行辅助观察[6],经过16次动态发射试验,确定了低速段(<1 000m/s)及高速段机械热和焦耳热在电枢表面磨损过程中的占比,分析了电枢表面的磨损规律,然而研究方法对轨道损伤严重,也无法从机理上对电枢表面磨损的影响因素进行解释。综上所述,电枢磨损过程的准确分析对提高电枢性能具有重要意义,但是现有电枢表面磨损量分析方法难以兼顾磨损量计算的准确性及分析过程的高效性,且仅采用试验也难以对发射过程中电枢磨损量的控制提供优化方向。
基于上述情况,本文首先分析了动态发射过程中电枢表面熔化磨损过程,厘清了相关耦合因素,在此基础上建立了计算电枢尾翼磨损量的理论及有限元分析模型,可考虑温度、接触力与磨损量间的耦合迭代关系,不仅可以提高计算效率,也能较为全面地考虑各因素对电枢尾翼磨损量的影响,为电枢结构性能的改进及枢轨接触性能的改善提供了有效的技术途径。
1 电枢动态磨损过程分析及磨损特点
1.1 电枢动态磨损过程分析
电枢动态磨损过程如图1所示,动态发射过程中,电流经电枢流入导轨时,由于枢轨接触面间存在接触电阻,因而会产生焦耳热;另一方面,电流通过磁场在电枢尾翼产生极大的电磁扩张力,随着电枢的高速运动,枢轨接触面间产生极大的机械摩擦热。在焦耳热及摩擦热的共同作用下,电枢表面温度急剧上升,一旦超过材料熔点,就会发生熔化,产生磨损[7-13]。因此,电枢表面磨损量是在电因素及力因素的共同作用下产生的。
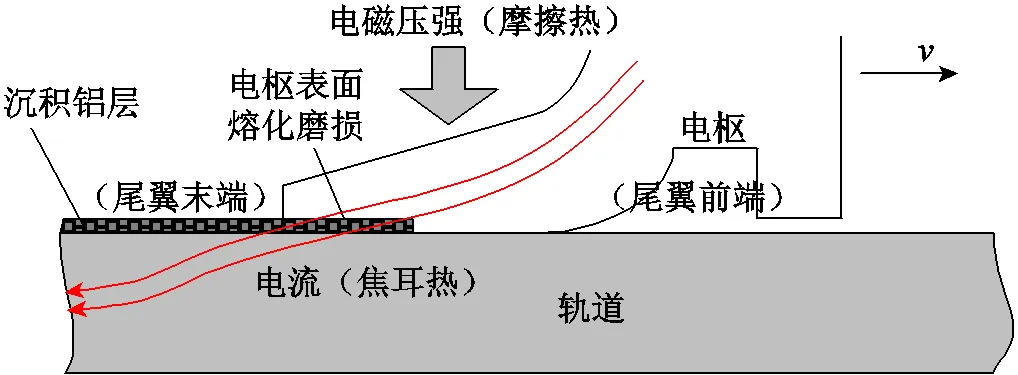
图1 电枢动态磨损过程分析
1.2 电枢尾翼磨损量分布特点
C形电枢由于结构简单及性能可靠,是目前研究的重点,因此本文主要针对C形电枢磨损量进行分析。电驱X光照片及其尾翼磨损特点如图2和图3所示。根据对试验过程中炮口电枢X光照片的分析可知[14],电枢表面磨损并非如图3a中平均磨损模型所示的从尾翼末端到前端为均匀磨损,实际上电枢尾翼末端磨损量最大,越靠近头部磨损量越小,且近似线性变化,如图3b中的线性磨损模型所示。

图2 电枢X光照片
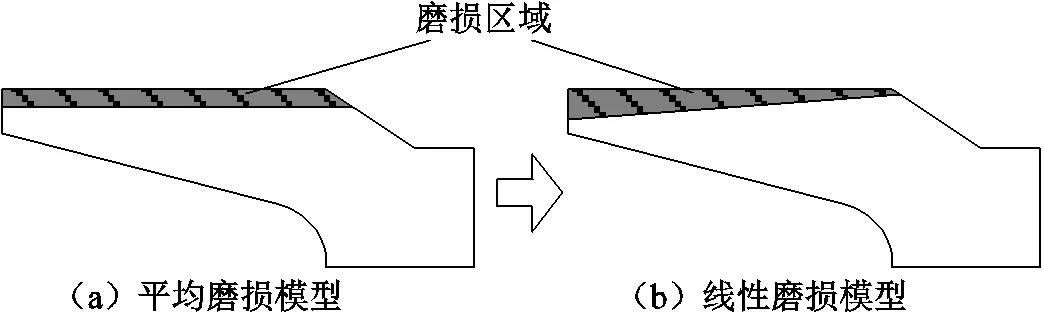
图3 电枢尾翼磨损特点
2 电枢尾翼磨损量理论分析模型
动态发射过程中枢轨接触面间所产生热量的主要来源为焦耳热j及摩擦热f,同时,接触面间的热量也会分别传导给轨道和电枢,假设分别为r和a,因此有

另设单位时间内电枢的熔化量为f,则

式中,a为电枢材料熔化潜热;a为电枢材料比热容;m为材料熔点;0为初始温度。
设单位时间内电枢的熔化体积为a,电枢材料密度为a,则
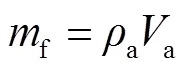
设时刻电枢的运动速度为,枢轨接触面总面积为c,则a=c,因此可得电枢尾翼表面平均磨损率

由式(4)可知,得到的关键是根据式(2)求解传导给电枢的热量a。假设馈电电流为,枢轨接触面间的接触电阻为c,则

假设动态发射过程中枢轨接触面间的摩擦系数为,枢轨间接触力为c,则
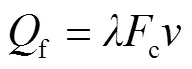
因此,由以上分析可知
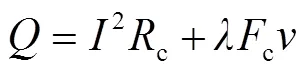
分析可知,动态发射过程中传导进入轨道的总热功率为[15]
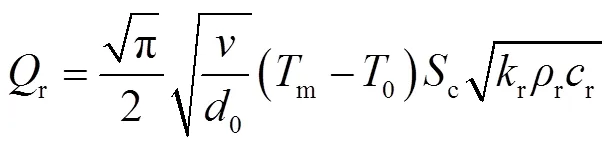
式中,r为轨道的热导率;r为轨道材料密度;r为轨道材料比热容;0为电枢臂长。
联立式(4)~式(8),得
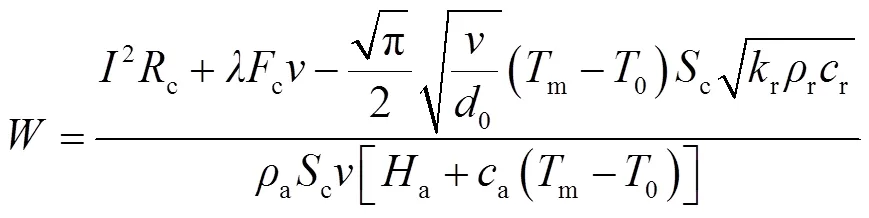
由式(9)可知,与电枢尾翼表面磨损率相关的影响因素包括馈电电流、电枢运动速度、枢轨间接触力c、电枢尾翼表面尺寸0和c,以及与电枢和轨道材料属性相关的潜热a、比热容r及a、熔点m和热导率r等。
2.1 焦耳热
焦耳热与枢轨间的接触电阻值有关,文献[16]中介绍了两种表征接触面电阻的模型:接触面热通量模型(Contact Surface Heat Flux Model, CSHFM)和接触层模型(Contact Layer Model, CLM)。本文采用CLM对枢轨界面间的接触电阻进行计算,该模型假设接触区域具有一定厚度的接触层,接触电阻率与接触压强相关,则
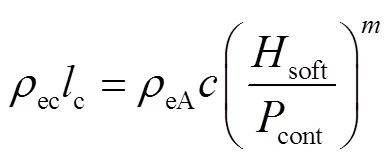
式中,ec为接触电阻率;c为接触层厚度;soft为电枢材料硬度;cont为接触压强;和为接触常数,可取1×10-3,而的数值通过试验获得;eA为枢轨接触对的平均接触电阻率,设电枢及轨道材料的电阻率分别为ea和er,则有
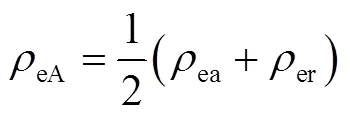
枢轨接触面积为c,因此,接触电阻c为

2.2 机械摩擦热
枢轨接触面间所产生的机械摩擦热与枢轨接触力c有关。由于电枢在运行过程中,一方面在电磁力作用下产生电磁扩张力,设其垂直于轨道的分量为n;另一方面,电枢表面产生磨损后,在电磁力作用下,磨损后的尾翼需要克服本身刚度影响发生形变贴紧轨道,以继续保持枢轨间的良好接触,发生形变的反向受力inv会抵消一部分垂向电磁力分量n。因此,两者的合力才是真正的枢轨接触力,即
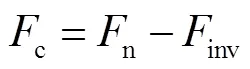
式中,n会受到磨损量的影响,inv会受到温度影响,下面分别对两个分量进行分析。
2.2.1 磨损量对电磁扩张力垂向分量n的影响
随着电枢磨损量的增加,电枢结构尺寸发生变化,进而会影响电磁扩张力的垂向分量n,电枢结构如图4所示。图中,0为电枢臂长,1为头部最小厚度,2为尾翼厚度,为尾翼倾角,为两轨道间距。
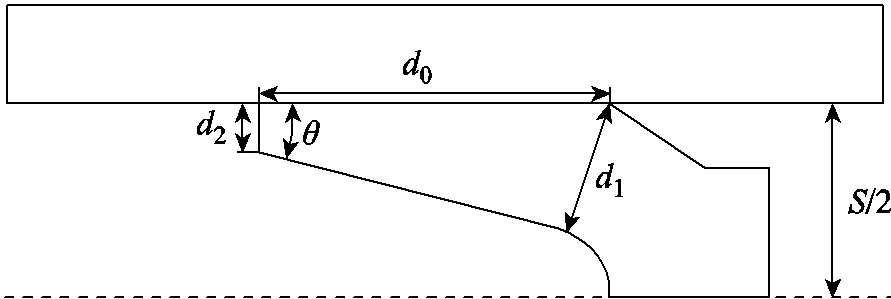
图4 电枢结构示意图
电枢受力分析如图5所示,可知电枢尾翼的垂向受力n为电磁扩张力EM的分量,采用文献[17]中的方法可对n进行近似计算,即
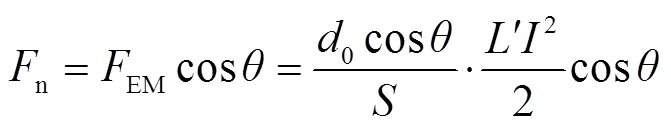
图5 电枢尾翼受力分析
Fig.5 Force analysis of armature tail
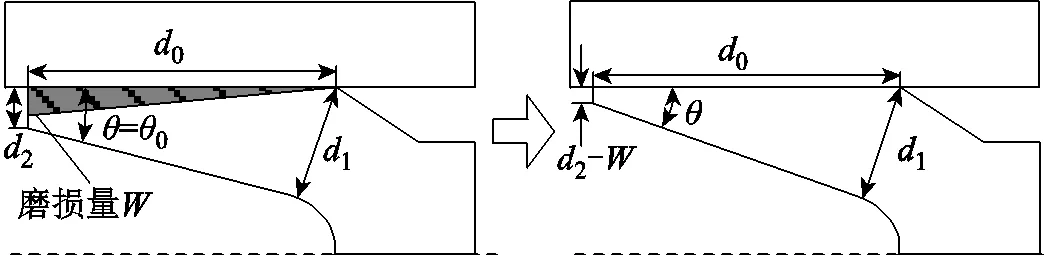
图6 电枢磨损后尾翼倾角
当磨损量为时,电枢尾翼倾角的表达式为

2.2.2 电枢温度升高对尾翼反向受力inv的影响
随着电枢的动态运行,在本体焦耳热的作用下,其弹性模量会逐渐降低,即弹性模量值会随温度的变化而变化,则有
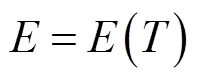
式中,为电枢材料弹性模量。通过查阅文献[18]中的实测结果,可知弹性模量随温度变化的关系如图7所示。
图7 温度与弹性模量的变化关系
Fig.7 The relationship between temperature and elastic modulus
动态发射过程中,电枢本体的温度呈现出非均匀分布的特点,不考虑磨损,发射结束后电枢表面温度分布如图8所示。
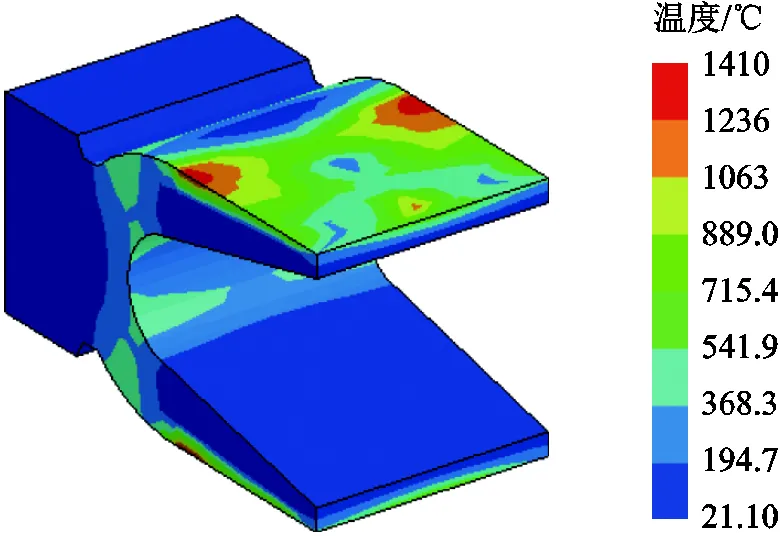
图8 发射结束时电枢温度分布
因此,可通过提取电枢节点温度值,计算本体的平均温度分布。在实际分析过程中,为便于编程计算,电枢本体的平均温度计算方法为[19]
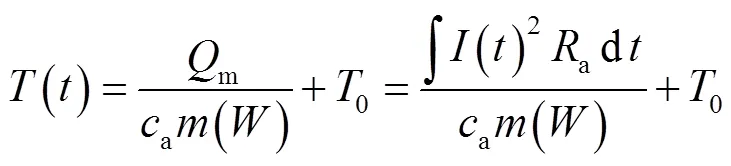
式中,()为考虑磨损后的电枢质量。
根据计算得到的电枢本体平均温度,采用式(16)得到对应的弹性模量,进而分析实际的枢轨接触力。根据图4中的电枢结构参数,可计算得到当电枢尾翼磨损量为时,其本体质量()为
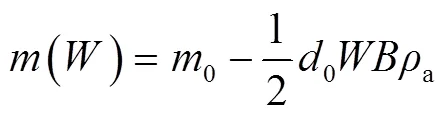
式中,0为电枢本体初始质量;为电枢本体宽度。
电枢发生形变所产生的反向受力inv可以通过悬臂梁模型进行分析。文献[20]对电枢形变进行了详细的分析,本文中为便于编程计算,将inv视为集中力,采用简化模型进行分析,如图9所示,即可得到反向受力inv为
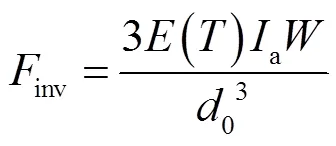
式中,a为电枢臂横截面惯性矩,其近似为
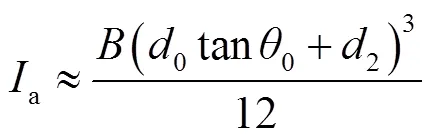
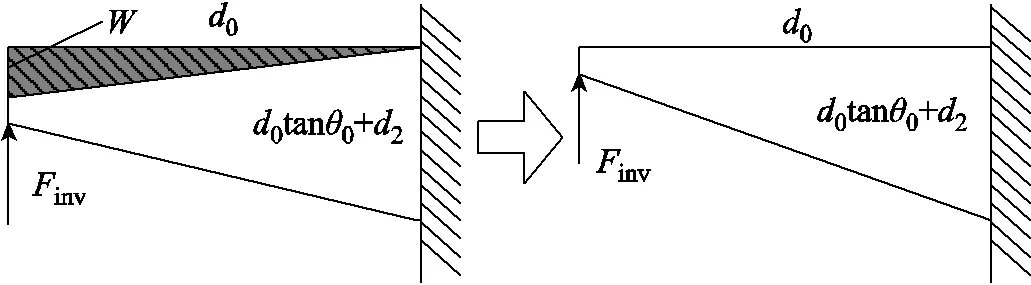
图9 电枢尾翼悬臂梁模型
2.2.3 考虑温度及磨损量影响的枢轨接触力计算
综上所述,枢轨间接触力c可采用式(13)进行计算。另外,由上述分析可知,温度的变化会引起本体弹性模量的变化,弹性模量及磨损量的变化会影响枢轨接触力,而枢轨接触力的变化又会反过来影响电枢本体的磨损量,磨损后又导致电枢本体的温度也会发生变化。因此,温度、磨损量及接触力c互相影响,在计算过程中存在耦合迭代的关系,需要编写程序对枢轨接触力进行求解。上述三者的变化关系如图10所示。
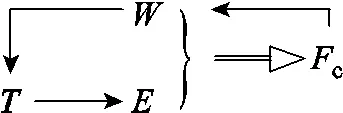
图10 各变量间的耦合关系
2.3 电枢磨损量理论计算模型
在上述工作基础上,建立电枢尾翼磨损量理论计算模型,其计算过程如图11所示。

图11 电枢尾翼磨损量计算模型
通过本文建立的理论模型计算得到的为平均磨损量,如图3a所示,采用等体积转换方式,可转换为线性磨损模型,进而得到尾翼末端的真实磨损量。同时,为了验证上述计算方法的正确性,可将计算结果与实测值进行对比,试验电流波形如图12所示。
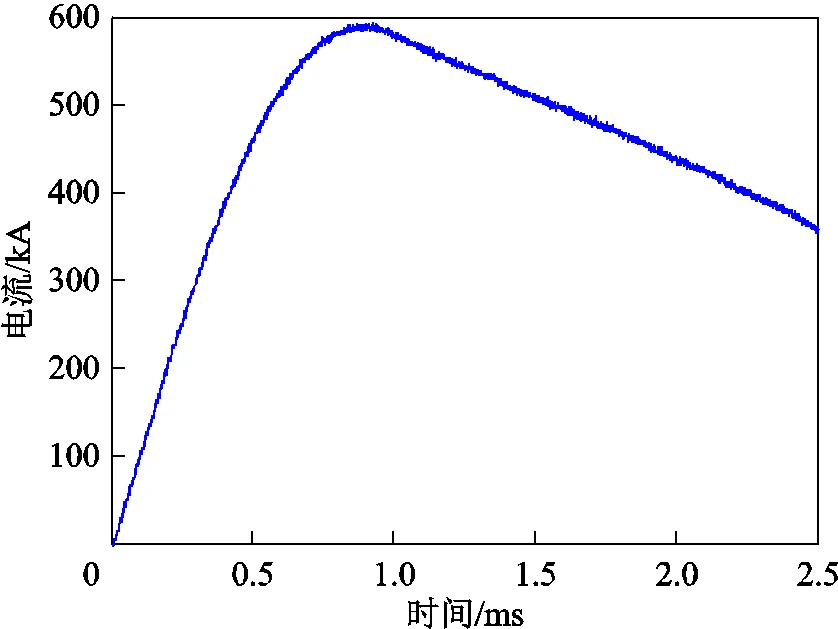
图12 电流波形
动态发射过程中,试验中所使用的弹丸关键尺寸如图4所示,质量0=0.078kg,其关键参数见表1。
表1 电枢及轨道结构关键参数

Tab.1 Key structure parameters of armature and rail
采用上述工况对电枢磨损量进行分析,电枢运动速度及位移曲线如图13所示。由图可知,弹丸运动距离约为2.111m,出口速度为1 806m/s。
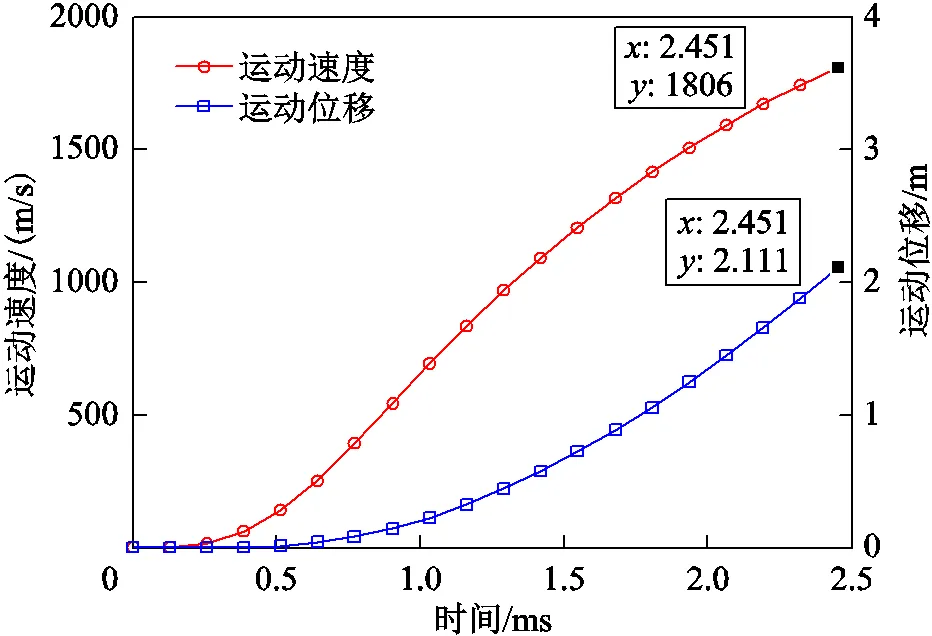
图13 电枢运动速度及位移曲线
电枢尾翼磨损量如图14所示,在约0.56ms前电枢尾翼磨损量均为负值,表示电枢在此刻才开始出现磨损,这是因为在电枢起动过程中,当枢轨接触面间的温度超过电枢材料熔点时才会使电枢表面出现熔化,产生磨损。分析可知,此时电枢运动距离约为32mm。图15为动态发射结束后的轨道表面铝层分布,可知在距离电枢起始位置约37mm处才开始出现铝层(图15中推弹头距离铝层出现位置约10mm,电枢尾翼长度为27mm,因此开始出现铝层的位置距离起始位置约为37mm),验证了所建立模型的正确性。图16为试验后回收电枢。回收电枢尾翼长度为27mm,表明电枢尾翼未被完全磨损,尾翼剩余厚度约为0.56mm,因此磨损厚度为1.94mm。应用本文所建立的理论分析模型,即考虑磨损量变化及反向受力等因素影响,计算得到电枢尾翼磨损量为1.992mm,与实测结果接近,进一步证明了所建立模型的正确性。另一方面,未考虑磨损量变化及反向受力等因素影响时,电枢尾翼磨损量计算值为2.475mm,较实测值大。因此,上述影响因素对电枢尾翼磨损量的影响不可忽略。

图14 电枢尾翼磨损量

图15 起始段轨道表面铝层

图16 回收电枢照片
3 电枢磨损量有限元分析模型
在上述分析结果的基础上,为了对电枢尾翼磨损量进行更为准确的分析,考虑电磁场-温度场-应力场及磨损的影响,在有限元软件中建立电枢表面磨损分析的三维有限元分析模型。在分析过程中,为提高效率,采用1/4模型,其网格划分如图17所示。

图17 电枢及轨道网格划分
对动态发射过程进行分析,不同时刻电枢尾翼磨损状态如图18所示。
分析结果表明,有限元模型能够准确模拟电枢尾翼末端磨损量大、头部磨损量小的线性磨损特征,且在开始运动后的0.5ms时,电枢表面未发生磨损,随着发射过程的进行,电枢表面逐渐出现磨损,且电枢尾翼在向外扩张的过程中,对喉部进行拉伸,进而产生应力集中,这也是前面所分析的反向受力的来源。在电枢出口前2.4ms时,电枢尾翼磨损量达到最大,但因为下降沿阶段电流已大幅降低,因此应力也逐渐减小。不同时刻电枢尾翼磨损量的有限元与理论模型计算结果对比如图19所示,试验结果、有限元及理论模型分析结果汇总见表2。
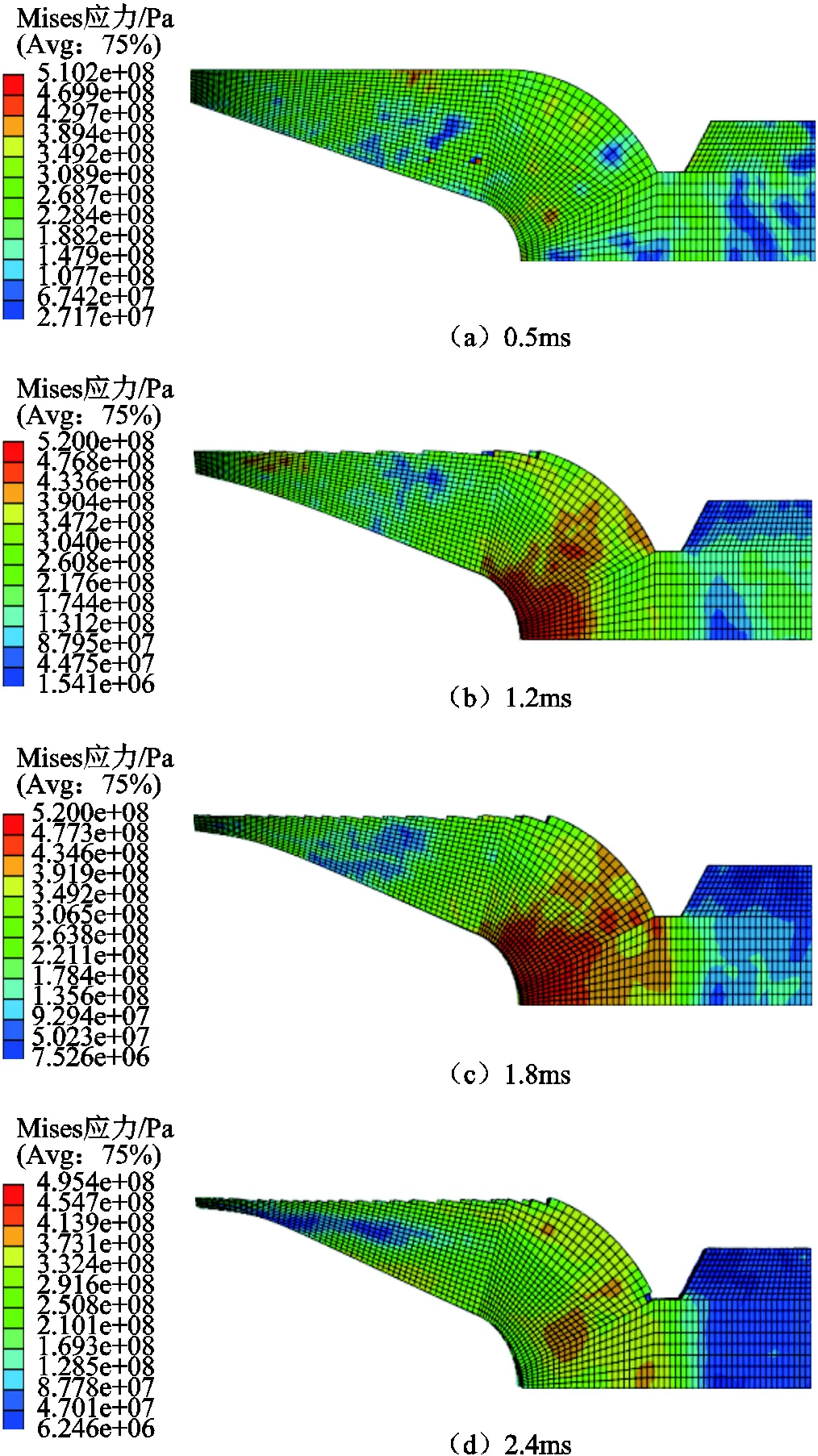
图18 不同时刻电枢磨损状态
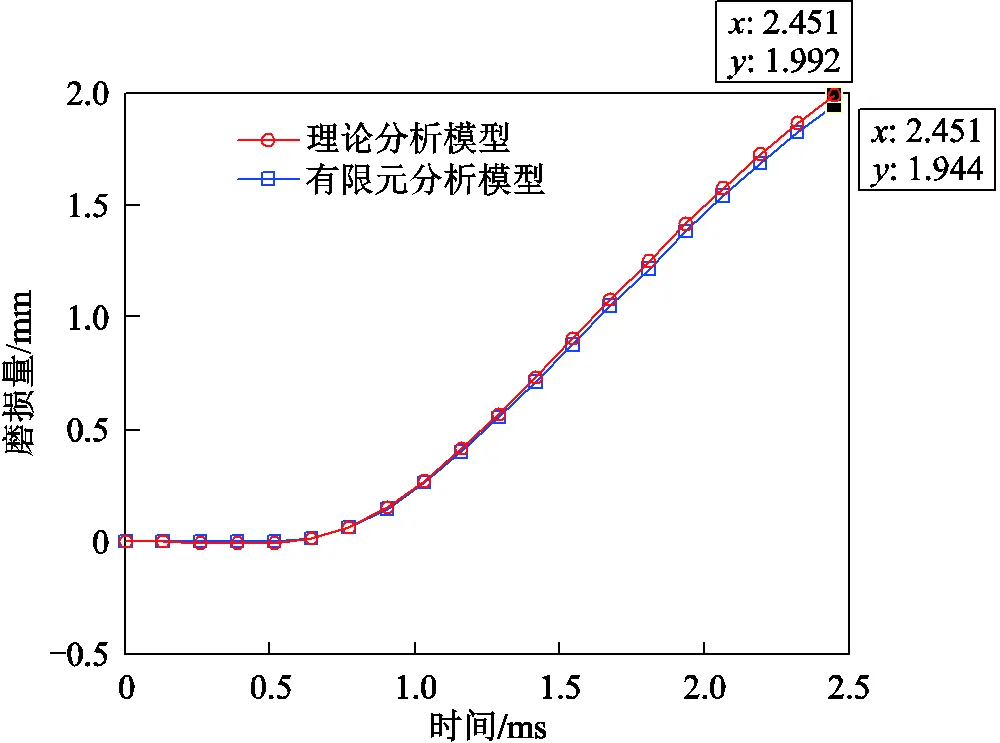
图19 理论分析模型及有限元模型计算结果对比
表2 电枢尾翼磨损量分析结果汇总

Tab.2 Summary of analysis results of armature tail wear(单位:mm)
分析结果表明,采用有限元分析模型计算电枢出口尾翼的磨损量为1.944mm,与理论模型的分析结果及磨损量变化趋势基本一致,且与实测结果更为接近,验证了所建立模型的准确性。
4 结论
电枢磨损会严重影响动态发射过程中的枢轨接触状态及膛内发射安全性。本文在详细分析电枢动态磨损过程及磨损特点的基础上,厘清了磨损相关的耦合因素,建立了理论及有限元分析模型。在理论分析模型中创新性地考虑了枢轨间接触力随温度、磨损量的变化,得到了电枢动态磨损规律,在有限元分析模型中考虑了电枢边磨损边扩张所带来的反向受力影响,对电枢尾翼的磨损量进行了更为准确的计算,并通过与实测结果进行对比,证明了所建立模型的准确性。本文的分析结果,对于后续电枢结构性能的优化具有重要意义。
[1] 关晓存, 鲁军勇, 张晓, 等. 基于热传导原理电枢平均磨损率计算[J]. 强激光与粒子束, 2013, 25(10): 2747-2752.
Guan Xiaocun, Lu Junyong, Zhang Xiao, et al. Calculation of average wear rate in armatures based on heat conduction principle[J]. High Power Laser and Particle Beams, 2013, 25(10): 2747-2752.
[2] 关晓存, 鲁军勇. 脉冲电流作用下枢轨接触面瞬态摩损量计算[J]. 强激光与粒子束, 2014, 26(11): 225-230.
Guan Xiaocun, Lu Junyong. Transient wear capacity calculation of armature-rail interface in pulse current[J]. High Power Laser and Particle Beams, 2014, 26(11): 225-230.
[3] Benton T, Stefani F, Satapathy S, et al. Numerical modeling of melt-wave erosion in conductors railgun armatures[J]. IEEE Transactions on Magnetics, 2003, 39(1): 129-133.
[4] Stefani F, Merrill R, Watt T. Numerical modeling of melt-wave erosion in two-dimensional block armatures[J]. IEEE Transactions on Magnetics, 2005, 41(1): 437-441.
[5] Chen Lixue, He Junjia, Xiao Zheng, et al. Experimental study of armature melt wear in solid armature railgun[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1142-1146.
[6] Stefani F, Parker J V. Experiments to measure wear in aluminum armatures in railguns[J]. IEEE Transactions on Magnetics, 1999, 35(1): 100-106.
[7] 李白, 鲁军勇, 谭赛, 等. 滑动电接触界面粗糙度对电枢熔化特性的影响[J]. 电工技术学报, 2018, 33(7): 1607-1615.
Li Bai, Lu Junyong, Tan Sai, et al. Effect of interfacial roughness of sliding electrical contact on the melting characteristics of armature[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1607-1615.
[8] 阮景煇, 陈立学, 夏胜国, 等. 电磁轨道炮电流分布特性研究综述[J]. 电工技术学报, 2020, 35(21): 4423-4431.
Ruan Jinghui, Chen Lixue, Xia Shengguo, et al. A review of current distribution in electromagnetic railguns[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4423-4431.
[9] 古刚, 吴立周, 耿昊, 等. 基于电磁-流场耦合的轨道冷却仿真分析[J]. 电工技术学报, 2020, 35(17): 3601-3608.
Gu Gang, Wu Lizhou, Geng Hao, et al. Simulation and analysis of rail cooling based on electromagnetic and fluid field coupling[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3601-3608.
[10] 张嘉炜, 鲁军勇, 谭赛, 等. 考虑初始接触压力的滑动电接触界面磁扩散模型[J]. 电工技术学报, 2022, 37(2): 488-495.
Zhang Jiawei, Lu Junyong, Tan Sai, et al. A magnetic diffusion model of electromagnetic launcher considering initial contact pressure[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 488-495.
[11] 杜佩佩, 鲁军勇, 冯军红, 等. 电磁轨道发射器电磁结构耦合动态发射过程数值模拟[J]. 电工技术学报, 2020, 35(18): 3802-3810.
Du Peipei, Lu Junyong, Feng Junhong, et al. Numerical simulation of dynamic launching process of electromagnetic rail launcher with electromagnetic and structural coupling[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3802-3810.
[12] 冯登. 电枢轨道高速滑动电接触界面热流体动力润滑研究[D]. 武汉: 华中科技大学, 2014.
[13] 汤亮亮. 电磁发射中枢轨接触界面金属液化层特性的实验与理论研究[D]. 武汉: 华中科技大学, 2015.
[14] Stefani F, Parker J. Experiments to measure armature wear, part 1: wear measurements on the kJ202 armature[R]. Institute for Advanced Technology The University of Texas at Austin, 1998.
[15] Balic E E. Melt wear control of metals in high-speed sliding contacts[D]. New York: Rensselaer Polytechnic Institute Troy, 2008.
[16] Hsieh K T, Satapathy S, Hsieh M T. Effects of pressure-dependent contact resistivity on contact interfacial conditions[C]//2008 14th Symposium on Electromagnetic Launch Technology, Victoria, British Columbia, Canada, 2008: 134-139.
[17] 王莹, 肖峰. 电炮原理[M]. 北京: 国防工业出版社, 1995.
[18] Satapathy S, Persad C. Thermal stress in EML rail-conductor overlays[J]. IEEE Transactions on Magnetics, 2001, 37(1): 269-274.
[19] Chen Lixue, He Junjia, Xiao Zheng, et al. Augmentation of current ramp-down contact pressure in C-shaped armature railguns[J]. IEEE Transactions on Plasma Science, 2011, 39(1): 48-52.
[20] Wang Lei.Modeling of the armature-rail interface in an electromagnetic launcher with lubricant injection[D]. Atlanta: Georgia Institute of Technology, 2008.
Research on Dynamic Wear Process of Armature Surface in High-Speed Sliding Electric Contact
Li Bai Lu Junyong Tan Sai Zhang Yongsheng Cai Xiyuan
(National Key Laboratory of Science and Technology on Vessel Integrated Power System Naval University of Engineering Wuhan 430074 China)
Armature is a key component of the electromagnetic launcher. During the dynamic launch process, its surface will be seriously worn, which will bring the following two problems: ① After the armature is worn and melted, it will form an aluminum layer in the bore, which will attach to the rail surface, increase the surface roughness, and affect the contact state between armature and rail during the subsequent launch process; ② After the tail is worn, the mechanical property that the armature can withstand is greatly weakened, which affects the launch safety. Therefore, it is of great significance to analyze the dynamic wear process of the armature surface in the high-speed sliding electrical contact process for controlling its surface wear, optimizing the armature structure, and improving the armature rail contact performance.
First of all, by studying the physical process between the armature and rail during dynamic launch process, the results show that under the combined action of Joule heat and friction heat during the launch process, the armature surface temperature will rise sharply. Once it exceeds the material melting point, it will melt and cause wear. Therefore, the wear of the armature surface is caused by the combined action of electrical factors and force factors. Through the analysis of the muzzle armature X-ray photos in the early stage, it is concluded that the wear of the armature surface is not uniform from the tail end to the front end. In fact, the wear of the tail end of the armature is the largest, and the closer to the head, the smaller the wear is, which is approximately linear. On the basis of the above analysis results, taking into account the influence of surface wear changes, temperature rise and reverse force during the outward expansion of the armature tail, a theoretical calculation model for the wear of the armature tail is established, and its wear laws are studied. The average wear of the end of the armature tail is obtained. Then, the equal volume conversion method is used to convert the model into a linear wear model, and then the real wear of the end of the tail is obtained. The results show that:, After considering the influence of factors such as the change of surface wear amount, temperature and reverse force during the outward expansion of the armature tail, the analysis shows that the armature surface wear amount is 19.5% less than that when it is not considered, but it is closer to the measured value after considering, which proves that the above influence factors cannot be ignored in the analysis process. Finally, considering electromagnetic field temperature field stress field wear and other coupling factors, a three-dimensional finite element calculation model is established to more accurately analyze the wear amount of the armature tail, and the finite element is compared with the theoretical calculation results. The results show that the finite element model is more accurate than the approximate calculation method for the normal force component and reverse force of the armature tail in the theoretical analysis model, The calculated wear of the armature tail is closer to the measured value, which verifies the accuracy of the model. The model and analysis results established in this paper will help to optimize the armature structure, improve the contact performance between the armature and the rail, and ensure the safety of projectile launching in the bore.
Electromagnetic launcher, armature, sliding electric contact, surface wear, coupling of multiple physical fields
10.19595/j.cnki.1000-6753.tces.211461
TM359.4
李 白 男,1989年生,助理研究员,研究方向为电磁发射技术。E-mail:libai1203@163.com
鲁军勇 男,1978年生,教授,博士生导师,研究方向为电磁发射技术、直线电机设计及控制技术。E-mail:jylu2019@163.com(通信作者)
国家自然科学基金(51925704,51877214,51607187,51907203)和湖北省自然科学基金(2020CFB341)资助项目。
2021-09-14
2022-02-22
(编辑 李冰)
