电磁互易定理一般形式

刘国强 刘 婧

电磁互易定理一般形式

刘国强1,2刘 婧1,2

（1. 中国科学院电工研究所 北京 100190 2. 中国科学院大学电子电气与通信工程学院 北京 100049）

现有互易定理对电磁场相互作用关系的描述是彼此独立的，该文利用四元数理论推导出了电磁互易定理的能动量时空统一形式，该形式中的实标部、虚标部、实矢部和虚矢部分别对应经典电磁互易定理即洛伦兹互易定理、Feld-Tai互易定理和新发现的两组动量互易定理。

互易定理 洛伦兹互易定理 Feld-Tai互易定理 动量互易定理

0 引言

自1896年洛伦兹提出洛伦兹互易定理[1]以来，一些新的电磁互易定理陆续被发现，包括频率域和时间域的互易定理。单就时谐场频率域互易定理而言，主要有Feld-Tai互易定理[2-3]、动量互易定理[4-6]和另一组动量互易定理[6]。通过分析洛伦兹互易定理、动量互易定理等可知，互易积分方程中的体积分项通常被写成两部分，一部分表示场源的“反应”关系，另一部分是某种“流密度”物理量（如能流密度、动量流密度等）的散度形式。通过高斯散度定理，散度的体积分项可化成面积分项。当两种源处于同一体积内或同一体积外，这个面积分项就可以消去，使得公式非常简洁，便于应用。目前，各个电磁场互易定理被认为是彼此独立的方程，本文旨在通过一种理论框架将上述各定理统一起来。

在《电磁通论》中，麦克斯韦使用了四元数，并将之用于电磁场方程。后来四元数理论成为矢量运算和矢量分析的前身。现在用四元数处理电磁场问题已不多见，尽管如此，根据狭义相对论，电磁场和源均是时空中的四物理量，四元数电磁场方程的实标部、虚标部、实矢部和虚矢部四个分量分别对应高斯电通定律、高斯磁通定律、安培定律与法拉第电磁感应定律。可以推测，利用四元数电磁场方程可以获得电磁互易定理方程，这个方程应该可以囊括现有的各种互易方程。

本文从四元数理论出发，推导了四电磁互易定理的一般形式，从中取出实标部、虚标部、实矢部和虚矢部各分量，分别对应了洛伦兹互易定理、Feld-Tai互易定理、两组动量互易定理。

1 四元数预备知识

1.1 四元数运算

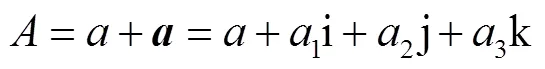
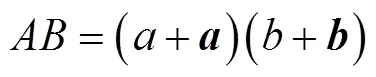
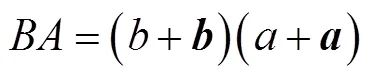
式中，任意两个虚数单位相乘，满足

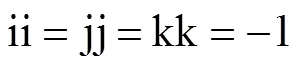
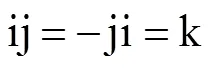
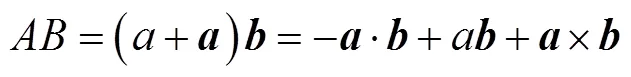
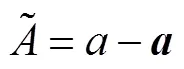
1.2 四元数电磁场

四电磁源的体密度为

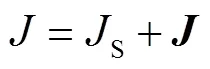
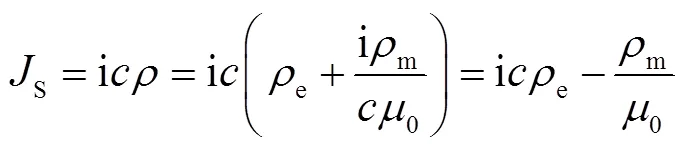
真空四电磁场为

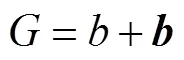
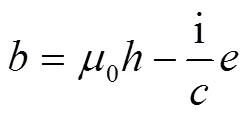
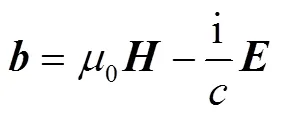
式中，为磁场强度；为电场强度。

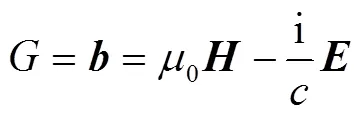
四梯度算子为

对于时变电磁场，为

对于时谐电磁场，为

真空中四电磁场方程为

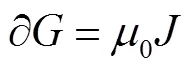
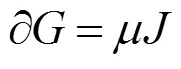
2 四元数电磁场互易定理

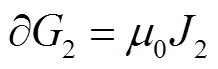
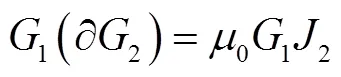
式（13）和式（14）两式相减，有

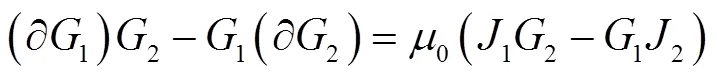
将式（15）的左端两项分别展开，有

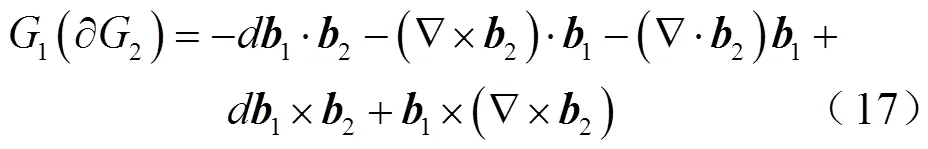
式（16）和式（17）相减，并应用附录恒等式

则有

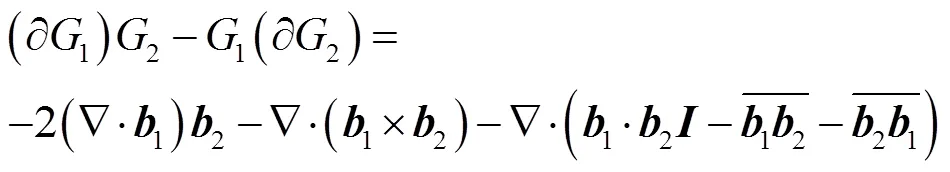
由于

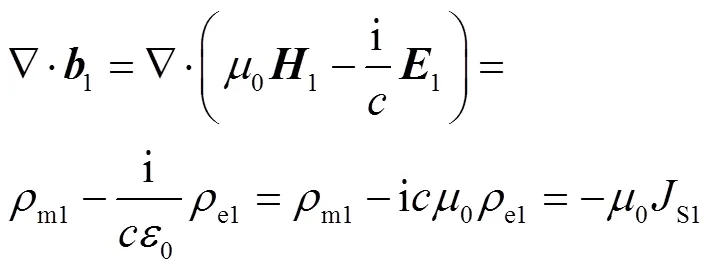
因此有

联合式（15）和式（21），有

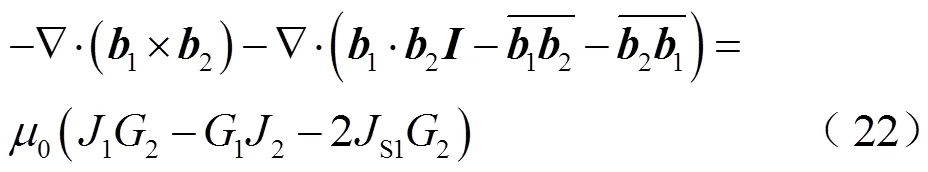
将式（22）的右端项改写为

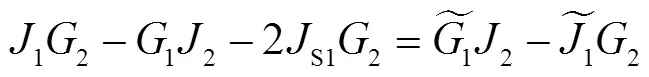
由式（9），则有

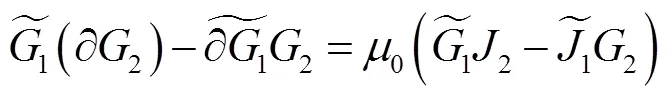
式（24）就是真空中四电磁互易定理的一般形式。为了看清楚它的“真面目”，将式（22）的右端项展开，于是式（22）化为

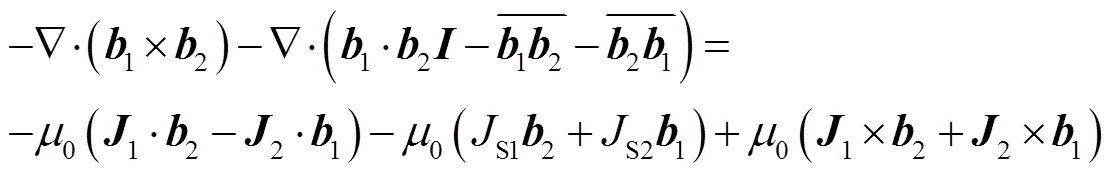
将四电磁场、四电磁源代入式（25），进一步展开式中各项，有

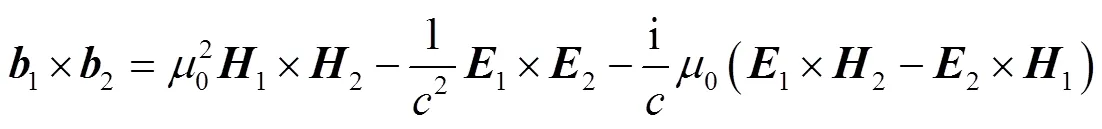
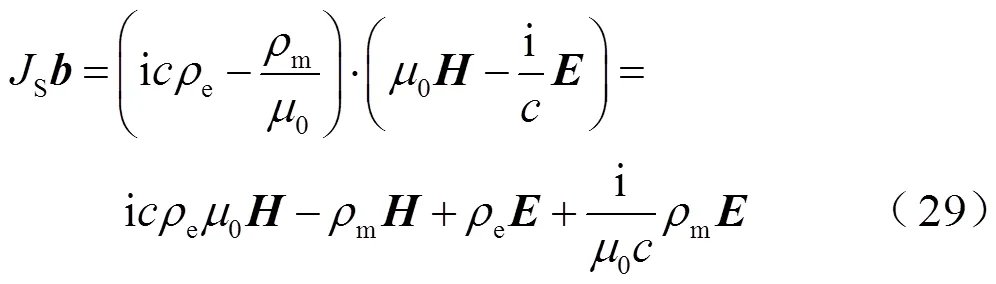
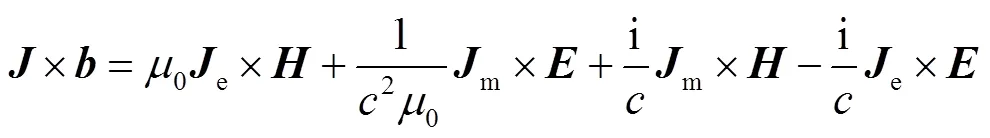
将式（26）～式（30）代入式（25），按实标部、虚标部、实矢部和虚矢部整理，则有

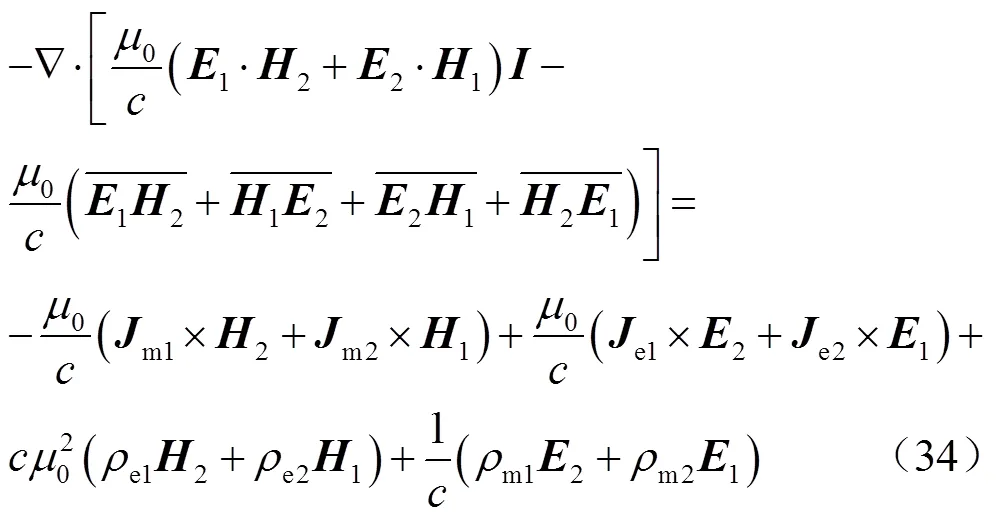
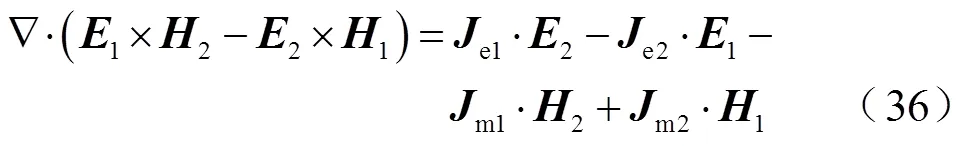
式（35）～式（38）中四个公式分别对应Feld-Tai互易定理、洛伦兹互易定理、动量互易定理和另一组动量互易定理。若对式（35）～式（38）各项作体积分，并利用高斯散度定理，各等式左端项化为面积分。可以证明，当两组源在同一体积内或同一体积外，面积分为零，公式非常简洁易用。

互易定理是工程电磁的理论分析和实际应用的有用工具[8]。例如，它可以用于惠更斯原理的导出[9]；为论证波导元件和天线的互易性提供了基础；常用于确定波导和空腔谐振器中波型间的正交性；也可作为电容层析成像[10]、热声成像[11]、磁声电成像[13]、磁声成像等多种图像重建方法的理论支撑。

3 结论

本文利用四元数理论，导出了电磁互易定理的能动量统一形式，反映了电磁场各个互易定理之间的时空统一联系。

附 录

证明：

矢量恒等式

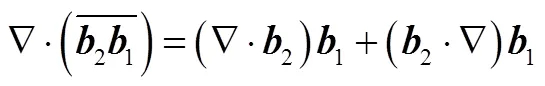
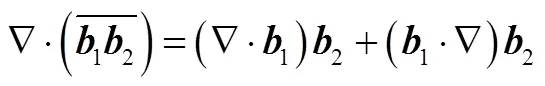
式（A2）和式（A3）两式相加有

另有

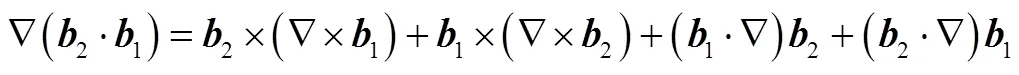
于是有

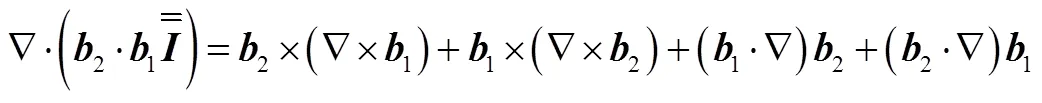
由式（A4）和式（A5），可得式（A1）。

[1] Lorentz H A . The theorem of Poynting concerning the energy in the electromagnetic field and two general propositions concerning the propagation of light[J]. AmsterdammerAkademie der Wetenschappen, 1896, 4: 176.

[2] Feld Y N. On the quadratic lemma in electrodynamics[J]. Soviet Physics-Doklady, 1992, 37: 235-236.

[3] Tai C T. Complementary reciprocity theorems in electromagnetic theory[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(6): 675-681.

[4] Lindell I V, Sihvola A H. Rumsey's reaction concept generalized[J]. Progress in Electromagnetics Research Letters, 2020, 89: 1-6.

[5] Liu Guoqiang, Li Yuanyuan, Liu Jing. A mutual momentum theorem for electromagnetic field[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(12): 2159-2161.

[6] 刘国强, 刘婧, 李元园. 电磁场广义互易定理[M]. 北京: 科学出版社, 2020.

[7] 许方官. 四元数物理学. 北京: 北京大学出版社. 2012.

[8] 符果行. 工程电磁理论方法. 北京: 人民邮电出版社, 1991.

[9] 刘国强，刘婧. 利用电磁场动量互易定理导出惠更斯原理[J]. 物理学报, 2022, 71(14): 140301.

Liu Guoqiang, Liu Jing. Huygens’ principle derived by using momentum reciprocity theorem of electromagnetic field[J]. Acta Physica Sinica, 2022, 71(14): 140301.

[10] Zhao Qing, Li Jie, Liu Shi, et al. The sensitivity optimization guided imaging method for electrical capacitance tomography[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-15.

[11] 郭亮, 王祥业, 姜文聪. 基于生成对抗网络的注入电流式热声成像逆问题研究[J]. 电工技术学报, 2021, 36(增刊1): 22-30.

Guo Liang, Wang Xiangye, Jiang Wencong. The study on the inverse problem of applied current thermo-acoustic imaging based on generative adversarial network[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 22-30.

[12] 李彩莲, 李元园, 刘国强. 基于磁声电技术的肺部组织成像仿真研究[J]. 电工技术学报, 2021, 36(4): 732-737.

Li Cailian, Li Yuanyuan, Liu Guoqiang. Simulation of lung tissue imaging based on magneto-acousto-electrical technology[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 732-737.

[13] 马任, 周晓青, 张顺起, 等. 磁声成像系统矩阵特征值差异性仿真研究[J]. 电工技术学报, 2021, 36(4): 724-731.

Ma Ren, Zhou Xiaoqing, Zhang Shunqi, et al. Simulation study on the eigenvalue difference of the system matrix in magneto-acoustic tomography[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 724-731.

A General Form of the Electromagnetic Reciprocity Theorems

Liu Guoqiang1,2Liu Jing1,2

（1. Institute of Electrical Engineering Chinese Academy of Sciences Beijing 100190 China 2. School of Electronic, Electrical and Communication Engineering University of Chinese Academy of Sciences Beijing 100049 China）

The existing reciprocity theorems describe the electromagnetic field interaction relationships independently of each other.In this paper, a general form of electromagnetic reciprocity theorem is derived by using quaternion theoretical framework. The real scalar part, imaginary scalar part, real and imaginary sagittal part of this form correspond to the classical electromagnetic reciprocity theorem, i.e. the Lorentz reciprocity theorems, the Feld-Tai reciprocity theorem and two newly discovered momentum reciprocity theorems respectively.

Reciprocity theorems, the Lorentz reciprocity theorem, the Feld-Tai reciprocity theorem, momentum reciprocity theorems

10.19595/j.cnki.1000-6753.tces.211590

TM93

刘国强 男，1971年生，研究员，博士生导师，研究方向为电磁场理论与多物理场耦合成像。E-mail：gqliu@mail.iee.ac.cn（通信作者）

刘 婧 女，1990年生，副研究员，研究方向为电磁检测与成像。E-mail：liujing@mail.iee.ac.cn

国家自然科学基金重点项目（51937010）和国家自然科学基金项目（51907191）资助。.

2021-09-29

2021-11-25

（编辑 郭丽军）