LISREL结构方程模型在语言研究中的应用❋
2023-01-30刘文慧
刘文慧
中南林业科技大学
周世界
大连海事大学
【提 要】结构方程模型是融合路径分析、多元回归分析和因素分析的多元统计方法,广泛用于心理学、社会学、教育学等多学科领域,但在国内语言研究领域应用不足。LISREL是一款主流结构方程建模分析软件,具有功能强、精确度高的特征。本文在介绍结构方程建模原理和特征基础上,通过LISREL9.2分析语言测试实例,介绍LISREL结构方程模型在语言研究验证性因子分析、全模型分析、高阶因子分析和多组验证性因子分析中的具体应用,证明LISREL结构方程模型能够为语言研究中不能直接测量的潜变量提供更精确的分析。
1 引言
在很多情况下,对教育、心理、社会等学科的研究涉及的变量(如自信、个性等)关系比较复杂,属于不能直接测量(候杰泰、温忠麟、成子娟2004)的潜在变量。对于这类变量的多元统计,结构方程模型(structural equationmodel,简称SEM)是一种方兴未艾的统计方法(Kline2005)。结构方程模型可以同时处理多个潜变量及其相互关系,并把变量测量误差计算在内,逐渐成为公认的分析潜变量间关系最强有力的现代统计方法,是行为心理学和教育学等领域常用的分析方法之一(Song&Lee2012;吴瑞林2013)。
目前,结构方程模型在语言研究中的应用主要涉及对语言能力、学习动机、学习态度等抽象概念和多个因素之间关系的研究。国外基于结构方程模型在二语习得等语言研究方面已经取得长足发展,如对语言能力测量(如Schoonen2005;Phakiti2008;Wallace&Lee2020)、语言习得个体差异(如Lee2005;Woodrow2006;Lee2020)和母语迁移影响(如Zhang2016;Maier,Bohlann&Palacios2016;Kimetal.2020)等研究。国内外语学界有关结构方程模型的研究虽然已经起步,但尚未充分展开。根据范劲松、任伟(2017)的调查结果,1999—2015年,国内12种外语类核心期刊发表的有关结构方程模型的论文只有52篇,其中实证性论文占90.4%(秦晓晴、文秋芳2002;彭剑娥2015);2016—2022年间,国内12种外语类核心期刊发表的有关结构方程模型的论文36篇,其中实证性论文占95%(如郑春萍、王丽丽2020;董连棋、刘梅华2022)。呈现上升趋势的数据说明国内语言学界越来越认识到结构方程模型的优势,但较小的数据量表明结构方程模型在语言研究中的应用仍然滞后。
LISREL(Linear Structural Relations)是 由Jöreskog(1979)开发并一直流行至今的专业结构方程建模分析软件,该软件在操作上很好地诠释了结构方程模型原理,分析结果精确度高,适用于处理语言教学中常见的基于连续变量的复杂调查数据及基于序数和连续变量的简单随机样本数据。但截至目前,国内语言学界只有王立非、鲍贵(2003)、王立非(2007)和韩宝成(2006)介绍了LISREL结构方程模型三种建模功能及其在语言测试领域的应用,但基本没有涉及具体应用方法。基于当前的研究现状,本文在阐述结构方程模型原理基础上,采用LISREL9.2软件,通过语言测试实例解析结构方程模型验证性因子分析、全模型分析、高阶因子分析和多组验证性因子分析的在语言研究中的具体应用,证明LISREL结构方程模型能够为语言研究提供更精确的统计分析。
2 结构方程模型原理
结构方程模型是根据变量的协方差矩阵或相关矩阵,通过多轮迭代计算样本矩阵与假设再生矩阵间的拟合指数,分析变量之间的关系。结构方程模型由测量模型(measurementmodel)和结构模型(structuremodel)两部分构成,测量模型处理观测变量(如测验分数、学习时间等)与潜变量(如语言能力、学习兴趣等)间的关系,结构模型主要处理潜变量间的关系。测量模型通常如公式(1)、(2)所示:
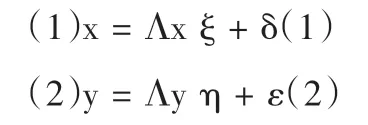
x和y分别表示外源变量和内生变量的观测变量,ξ和η表示外源潜变量和内生潜变量,Λx和Λy表示x和y的因子负荷矩阵,δ和ε表示x和y的误差项。结构模型的因果关系通常如公式(3)所示:

B表示内生潜变量间的关系,Γ表示外源潜变量对内生潜变量的影响,ζ表示结构方程的残差项。
结构方程模型分析一般包括模型建构、模型拟合、模型评估和模型修正四个过程:模型构建是根据相关专业理论和研究构建一个或几个结构方程模型,设定观测变量与潜变量间关系、潜变量间关系或限定因子参数值;模型拟合是用已构建的模型分析样本数据,找到样本协方差矩阵与模型隐含的协方差矩阵间的最小差距值;模型评估是通过检查结构方程的解是收敛、参数值与预测值是否相符、各拟合指数与界值差距等方法衡量模型拟合情况;模型修正是根据相关专业理论和参数值,以循序渐近的方式修改并确立最终模型。结构方程模型整合了路径分析、多元回归分析和因素分析,与传统统计分析方法相比有以下优势:(1)同时处理多个观测变量和潜变量,而传统统计方法每次只分析一对变量间的效应;(2)允许观测变量和潜变量含有测量误差,避免了传统回归分析默认误差为零而产生的实际相关系数被低估的错误;(3)同时估计因子结构和因子关系,克服了传统统计分析方法先分析因子负荷,再分析因子结构产生的不灵活问题;(4)允许包含更大弹性复杂测量模型,打破了传统因子分析难以处理一个测量指标从属多个因子的限制;(5)可以检验整个模型的拟合程度,而传统统计方法每次只估计一个路径关系的方式无法计算整个模型与观测数据的拟合程度(邱皓政、林碧芳2019)。LISREL结构方程模型默认采用极大似然法估计模型参数,找到样本协方差矩阵与结构方程再生矩阵间差距最小的参数(即拟合函数),在探讨多变量因果关系上优势显著。
尽管LISREL结构方程建模相比传统统计方法有诸多优势,可以更好地处理复杂模型的数据分析,但遗憾的是,由于诸多语言研究者对数据统计存在畏惧感,加上LISREL软件语法界面相对复杂,LISREL在我国语言研究领域的应用还比较欠缺。因此,本文通过外语测试实例,详细介绍LISREL结构方程模型在语言研究中的具体应用,为更多语言研究者了解和掌握这种功能强大的数据建模分析方法提供参考。
3 LISREL结构方程模型的语言研究应用
3.1 验证性性因子分析
因子分析(factoranalysis,又称因素分析)指从一组观测变量中提取具有代表性的共性因子(即潜变量)的统计方法,在社会科学研究中有广泛的应用。例如,通过外语学习者课堂发言次数、作业完成情况及课外学习时间等观测变量抽取是否存在学习积极性这一潜在变量。因子分析方法包括探索性因子分析(exploratory factor analyses,简称CFA)和验证性因子分析(confirmatory factor analysis,简称EFA)。探索性因子分析通过对观测变量的旋转和抽取,探索出未知的公共因子,旨在分析观测变量所内涵的潜在因子;验证性因子分析则是事先假设出观测变量所内涵的公共因子,通过统计分析结果验证假设与潜在因子从属关系的合理性。笔者以湖南省某高校大一年级学生的三次英语测试为例,介绍LISREL验证性因子分析在语言研究中的应用。
为了探索外语学习者英语口语、写作和阅读能力之间的联系,笔者选取高校一年级非英语专业6个自然班的164名学生为受试对象,剔除无效数据,最后收集了155名学生不同时段的三次英语口语、写作和阅读成绩(使用雅思测试题,每次测试时长、题型、题量和难度等同),根据研究目的和二语习得理论,建立结构方程模型如图1左图所示:

图1 验证性因子分析假设模型图及其路径系数
LISREL结构方程模型中,圆形代表潜变量或因子,方形代表观测变量或指标,单向箭头代表单向效应,双箭头弧形代表相关,单向箭头指向圆形或方形表示残差和测量误差。图1中,长方形内的SPK1,SPK2,SPK3分别代表三次口语成绩,WRT1,WRT2,WRT3分别代表三次写作成绩,RD1,RD2,RD3分别代表三次阅读成绩;椭圆形内的SPK代表口语能力,WRT代表写作能力,RD代表阅读能力。该模型包含以下假设:外语学习者英语测试成绩反映其口语、写作和阅读能力;外语学习者英语口语、写作和阅读能力间存在显著性相关。LISREL默认采用极大似然法估计模型参数,前提条件是变量数据服从正态分布。用SPSS20.0检查样本数据正态分布情况显示,9个变量的偏度绝对值小于3(在0.124-0.867之间),峰度绝对值小于8(在0.035-3.356之间),表明数据基本呈正态分布,满足LISREL数据分析条件。用SPSS20.0获得相关系数矩阵如表1所示:
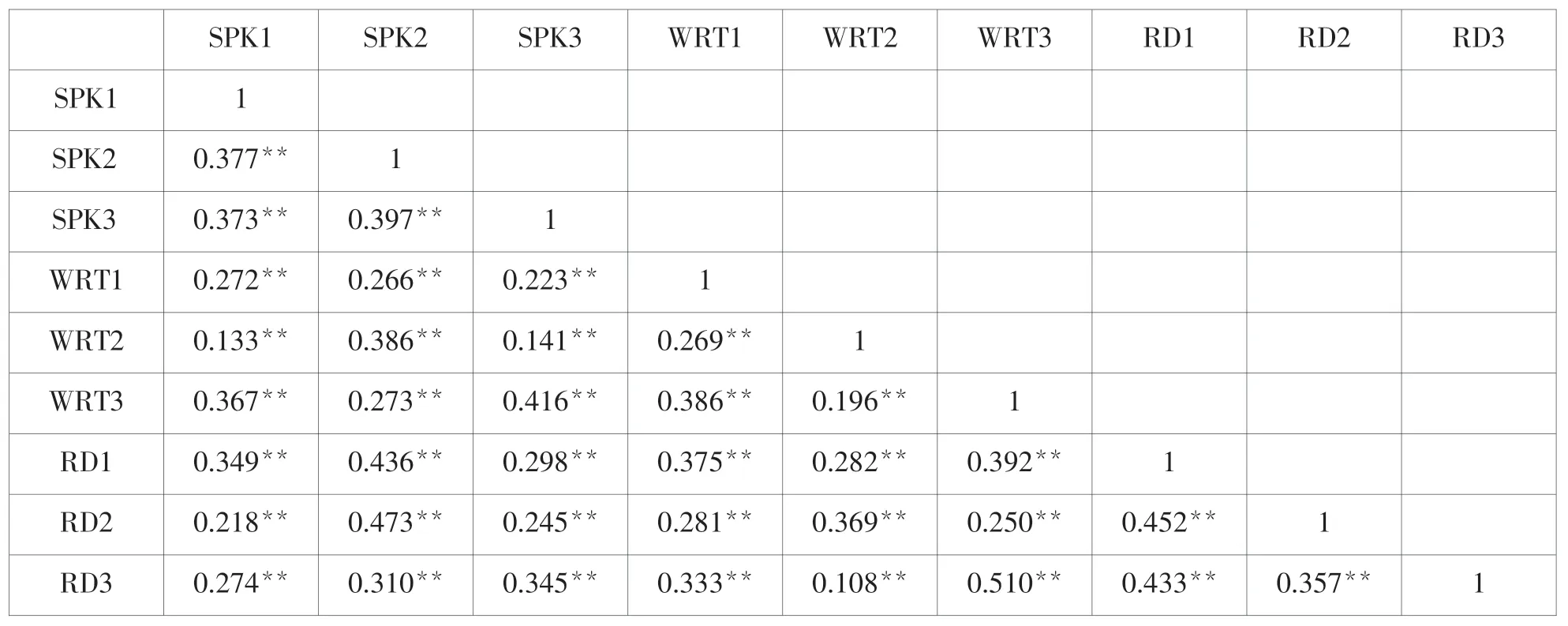
表1 三次测试成绩相关系数矩阵(N=155)
表1中,9个观测变量之间均存在显著性相关(p<0.01),表明原始观察值适合做结构方程模型验证性因子分析。在LISREL9.2程序窗口输入相应程序并运行,迭代9次后输出分析拟合指数结果如表2所示:
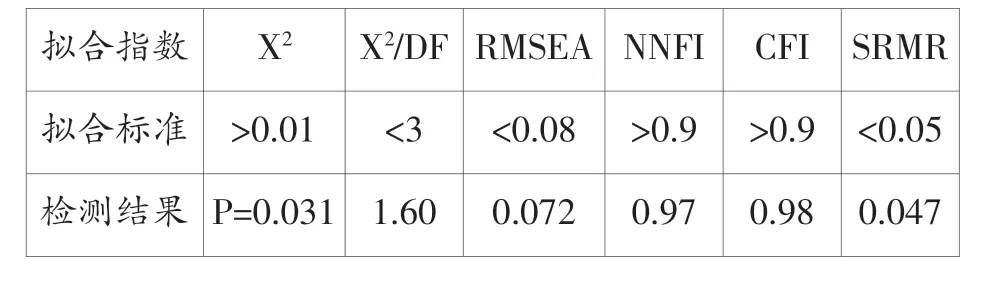
表2 验证性因子分析拟合指数
表2中,拟合指数是表示样本数据与假设模型拟合是否妥当的指数值。LISREL输出的拟合优度指数比较多,选取哪些拟合指数作参考是一个复杂的课题,至今没有绝对定论(侯杰泰等2004),一般认为如果至少有两个主要拟合指数在界值内,其它拟合指数接近界值就可以接受假设模型。根据前人的研究结果和本文实际情况,笔者选择X2(chi-square,卡方)、X2/DF(相对卡方)、RMSEA(rootmean squareerror of approximation,近似误差均方根)、NNFI(on-normedfitindex,非范拟合指数)、CFI(comparative fitindex,比较拟合指数)和SRMR(standardized rootmeans quareresidual,标准化残差均方根)作为参考拟合指数。本例样本数接近150,根据温忠麟、侯杰泰和马什赫伯特(2004)提出的X2准则,X2P值临界值为0.01。表2中,X2P(0.031〉0.01)、X2/DF(1.60<3)、RMSEA(0.072<0.08)、NNFI(0.97〉0.09)、CFI(0.98〉0.09)和SRMR(0.047<0.05)6个拟合指数都在建议界值范围内。此外,LISREL输出结果中各项修正指数均无异常显著值,说明假设的结构方程模型合理,不需要进行模型修正。综合各项拟合指数表现,可以认为图1假设的方程模型与样本数据拟合较好。LISREL输出的模型各路径系数如图1右图所示。根据Cohen(1988)的研究,相关系数大于0.5为高度相关,0.3-0.5为中等相关,小于0.3则是较低相关,模型中全部12个路径系数均大于0.5,说明各变量间相关度较高。由此,通过LISREL因子分析结果可以验证前面设立的英语能力关系假设成立,即外语学习者的测试成绩反映其口语、写作和阅读能力;外语学习者英语口语、写作和阅读能力相互之间存在显著性相关。该结果与前人的研究(文秋芳2006;刘文慧、阳志清2009)和实践教学经验相符,即在我国高等教育阶段,因为写作和阅读教学更倾向于书面语,所以阅读和写作呈现高度相关(0.89);但口语与写作和阅读之间的高度相关(0.83,0.89)表明外语学习者对英语口语和书面语之间的区分不敏感,导致口语有较严重的书面语倾向。
3.2 全模型
全模型(fullmodel,又称饱和模型)是指同时包含外源变量和内生变量的模型。笔者仍以上述实例中的样本观察值为例,介绍LISREL全模型分析在语言研究中的应用。
本例研究目的是在了解外语学习者英语口语、写作和阅读能力相关基础上,进一步探索英语阅读能力对口语和写作能力的影响。根据研究目的和二语习得理论,首先建立结构方程模型如图2左图所示。
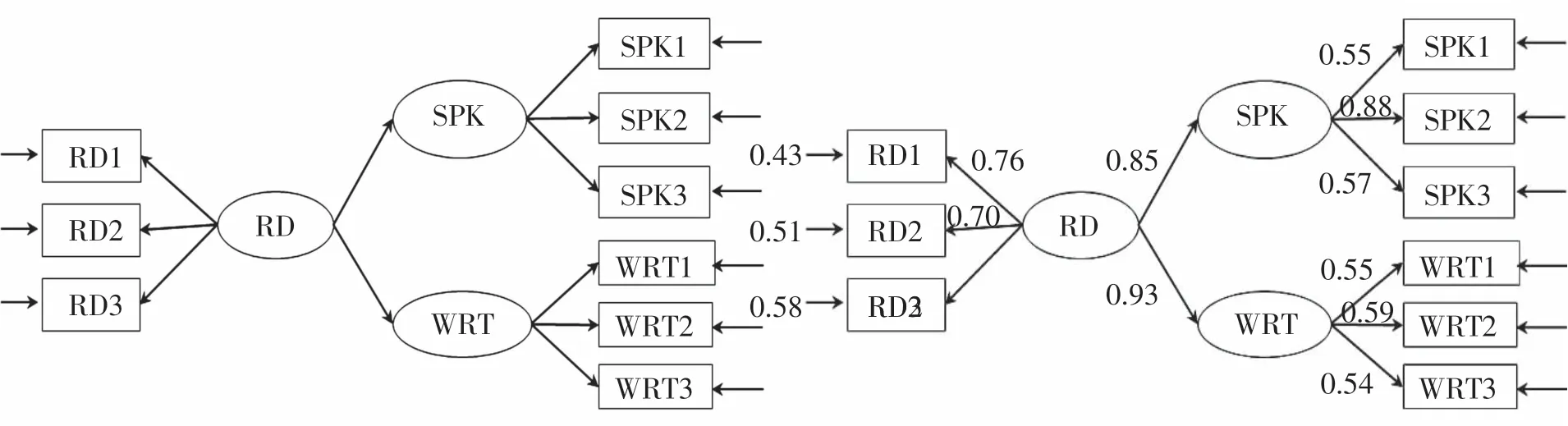
图2 全模型假设模型及其路径系数
该模型基于以下假设:外语学习者的三次测试成绩反映其英语口语、写作和阅读能力;外语学习者英语阅读能力对口语和写作能力有显著性影响。在LISREL9.2程序窗口输入相应程序并运行,迭代15次后输出分析拟合指数结果如表3所示:
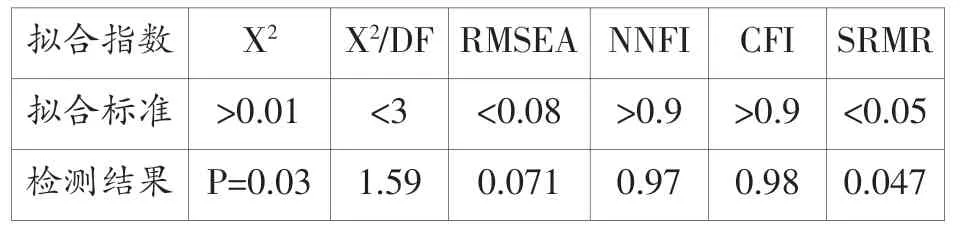
表3 全模型分析拟合指数
表3中,X2P值(0.03〉0.01)、X2/DF(1.59<3)、RMSEA(0.071<0.08)、NNFI(0.97〉0.9)、CFI(0.98〉0.9)和SRMR(0.047<0.05)6个拟合指数都在界值范围内。综合各拟合指数表现,可以认为图2所示方程模型与样本数据拟合较好。另外输出的分析结果中各项修正指数无异常显著值,说明假设的结构方程模型合理,无需进行模型修正。LISREL输出的模型各路径系数如图2右图所示,模型中全部11个路径系数都大于0.5,说明各变量间相关度较高。由此,通过LISREL全模型分析结果可以验证之前设定的英语能力关系假设的正确性,即外语学习者的测试成绩反映了其英语口语、写作和阅读能力;外语学习者英语阅读能力对口语和写作能力有显著性影响。其中,阅读对写作的影响大于口语(0.93〉0.85),该结果进一步证明外语学习者的阅读和写作能力呈现高度相关性。同时,阅读和口语的高度相关(0.85)也证明外语学习者不能很好地区分英语口语和书面语之间的差异。在未来外语教学中,教师应注意帮助学生意识到英语口语的书面语之间存在差异,在实际语言应用中应注意避免混淆这两种不同的语体。
3.3 高阶因子分析
高阶因子分析(higher-order factoranalysis)是将分析观测变量得到的因子作为观测变量进一步进行因子分析的统计方法,是全模型分析的一种特殊形式。高阶因子分析过程在理论上可连续进行,但由于三阶因子模型已经非常庞大和复杂,在现实研究中使用三阶因子及以上模型的情况比较少。需要注意的是,一阶因子数量在四个或以上时建立二阶因子才有简化模型的作用。另外,在建立二阶因子模型前要先检验变量的一阶因子模型,只有一阶因子间相关较强时,建立的二阶模型才有意义。笔者以湖南某高校大一年级学生的三次英语测试为例,介绍LISREL二阶因子分析在语言研究中的具体应用。
为了探索外语学习者英语综合能力的具体构成情况,笔者选取高校一年级非英语专业9个自然班的293名学生为受试对象,剔除无效数据,最后收集了281名学生不同时段的三次英语口语、写作成绩和二次听力、阅读成绩(使用雅思测试题,每次测试时长、题型、题量和难度等同)。用SPSS 20.0检查数据正态分布情况显示,10个变量的偏度绝对值小于3(在0.110-0.887之间),峰度绝对值小于8(在0.120-3.453之间),表明数据满足基本呈正态分布的分析条件。首先对样本数据进行类似图1模型的一阶验证性因子分析,输出结果显示一阶因子模型中各变量间呈显著性相关(相关负荷分别为0.83,0.90,0.82,0.83,0.86,0.93),表明原始观察值适合进行二阶因子模型分析。根据研究目的和二语习得理论,建立二阶因子方程模型如图3左图所示。

图3 二阶因子假设模型及其路径系数
图3中,SPK、WRT、LIS和RD分别代表外语学习者口语能力、写作能力、听力能力和阅读能力,ENG代表外语学习者的英语综合能力。该模型基于以下假设:外语学习者的考试成绩反映其英语口语、写作、听力和阅读能力;外语学习者英语口语、写作、听力和阅读能力构成其英语综合能力。在LISREL9.2程序窗口输入相关程序并运行,迭代24次后输出分析结果如表4所示:
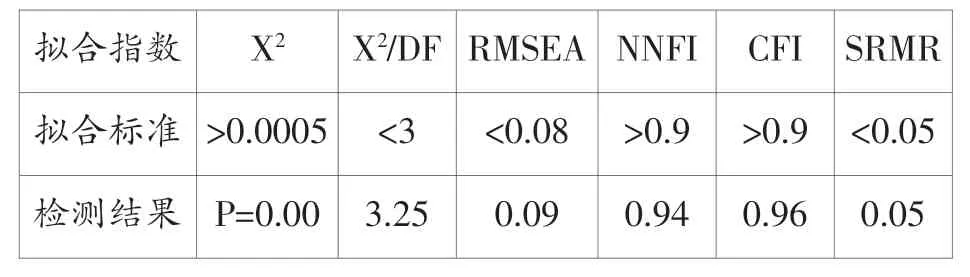
表4 二阶因子拟合指数
表4中,NNFI(0.94〉0.9)、CFI(0.96〉0.9)和SRMR(0.05=0.05)3个拟合指数均在建议界值范围内,X2/DF=3.25略大于界值3,RMSEA=0.09接近界值0.08。本例样本数281大于250,根据温忠麟等(2004)的X2准则,X2P值的临界值应为0.0005,表3中的X2P值0.00接近临界值0.0005。第四大列中有3个拟合指数在界值内,其他指数接近界值。综合各拟合指数表现,可以认为图3假设的方程模型与样本数据拟合较好。另外输出的分析结果中各项修正指数无异常显著值,说明假设的模型无需修正。LISREL输出的模型各路径系数如图3右图所示,模型中有13个路径系数大于0.5,有1个介于0.3-0.5之间,说明各变量间相关度较显著,尤其是ENG对SPK、WRT、LIS和RD的系数值都在0.8以上,说明相关性非常强。由此,通过LISREL二阶因子分析结果可证明原假设成立,即外语学习者的测试成绩反映了其英语口语、写作、听力和阅读能力;外语学习者英语口语、写作、听力和阅读能力构成其英语综合能力。其中,听力和阅读作为输入性语言能力,其相关性大于口语和写作两种输出性语言能力(0.97+0.95〉0.91+0.87),这一发现与语言教学实际经验一致。例如在雅思测试中,中国考生在写作和口语两项失分比较严重,尤其写作部分失分现象更加突出。数据分析结果表明,在未来外语教学中,教师需兼顾语言输入与输出能力均衡发展,在注重听力和阅读两种语言能力培养的同时,更需要加强对学生口语和写作能力的培养。
3.4 多组验证性因子分析
多组验证性分析(multiplegroup sconfirmatory factoranalysis)用来验证不同样本的是否来自同一个总体、是否有等同的因子结构。在多组验证性因子分析中,首先根据相关研究理论和相同测量工具(试卷、问卷等)确定一个大致可以适用于各组样本的模型,再检验各组样本间模型形态和因子负荷(LX)是否等同,在此基础上再依次检验各组样本的因子方差—协方差(PH)、测量误差方差—协方差(TD)、指标截距(TX)、因子均值(KA)等是否等同。在检验过程中,如果有一组样本或者某个步骤拟合欠佳,再做后面的检验就失去意义。如果各组拟合指标表现良好,并依次通过检验,则可以认为各组样本拥有相同的因子结构(侯杰泰等2004)。下面以湖南某高校两届大一学生的三次英语测试为例,介绍LISREL多组验证性分析在语言研究中的应用。
本例研究目的是验证不同级别外语学习者英语口语、写作和阅读能力间的关系是否等同。首先选取两届共272名非英语专业大一学生为受试对象(人数分别为155和117),收集不同时段的三次英语口语、写作和阅读成绩(使用雅思测试题,每次测试时长、题型、题量和难度等同)。根据研究目的和二语习得理论,建立如图1所示验证性因子结构方程模型。用SPSS20.0检查两组数据正态分布情况发现,9个变量的偏度绝对值均小于3(在0.110-0.887之间),峰度绝对值均小于8(在0.120-3.453之间),表明观测数据基本呈正态分布。通过SPSS20.0获得两组样本相关矩阵,发现除了第二组WRT2样本有个别数据没有呈现显著性相关(p〉0.01),两个样本组的9个观测变量之间均存在显著性相关(p<0.01),表明原始观测值适合做结构方程模型验证性因子分析。
首先分析两组模型形态是否等同。用LISREL多组设定的方法分组设定,LISREL9.2输出的拟合指数整理结果如表5形态项所示,X2P值(0.09〉0.01)、X2/DF(1.29<3)、RMSEA(0.05<0.08)、NNFI(0.98〉0.9)和CFI(0.99〉0.9)这5项拟合指数均在界值范围内,SRMR=0.05接近临界值,表明两个样本组的模型拟合良好,两样本组模型形态等同,可以继续下一步检验两组模型因子负荷是否等同。
在LISREL9.2中输入程序并运行,输出的拟合指数如表5形态、负荷项所示,X2/DF(1.61<3)、RMSEA(0.07<0.08)、NNFI(0.96〉0.9)、CFI(0.97〉0.9)和SRMR(0.04<0.05)这5个拟合指数都在界值范围内,只有X2P值0.002稍小于0.01。综合各项指数表现,支持两样本组模型形态和因子负荷等同假设,具备进行继续下一步检验条件。
在LISREL9.2中输入程序并运行,输出的拟合指数整理结果如表5形态、负荷、因子协方差项所示,除了X2/DF(2.5<3)、NNFI(0.91〉0.9)和CFI(0.93〉0.9)在建议值范围内,X2P值(0.00<0.01)、RMSEA(0.096〉0.08)和SRMR(0.18〉0.05)都不太理想,但因为有3个主要拟合指数在界值范围内,仍可以认为两样本组模型形态、因子负荷和部分因子相关等同,可以进一步验证两组样本模型因子协方差和误方差等同情况。
在LISREL9.2中输入程序并运行,输出的拟合指数整理结果如表5形态、负荷、因子协方差、误方差项所示,可以看到检验结果与预期相符,两个样本组的模型拟合程度大幅度恶化,其中X2值增大了318.18,X2P值(0.0)、X2/DF(6.71)、RMSEA(0.219)、NNFI(0.65)、CFI(0.66)和SRMR(0.22)都远离界值,检验结果不支持等同假设成立。

表5 多组验证性因子分析拟合指数
综上,LISREL多组验证性因子分析结果表明,两届大一学生样本组只在模型形态、因子负荷和部分因子间相关上存在等同关系。这个结果说明在外语学习中,在教学环境等基本等同条件下,不同届的学生语言能力在总体上呈现共性特征,但在测量误差方差—协方差、指标截距、因子均值等方面存在差异。研究表明不同届学生之间存在共性和个性差异,教师在教学过程中要从学生的实际情况出发,根据教学环境和学生认知学习特征调整教学方式。
4 结语
基于结构方程模型的统计原理,本文采用LISREL9.2软件,通过教学实例证实了结构方程模型在语言教学验证性因子分析、全模型分析、高阶因子分析和多组验证性分析中的具体应用,证实LISREL结构方程模型在探索语言研究多变量关系方面具有应用优势,为结构方程模型在语言研究中的应用提供实证依据。而本研究的局限在于仅考察了结构方程模型在课堂环境下语言习得中的应用,后续研究可加入课外环境下和诸如学习动机、学习时间、家庭影响等因素,为结构方程模型在语言研究领域更大范围内的应用提供参考。
虽然LISREL结构方程模型比传统统计方法有诸多优势,但结构方程模型在语言研究中的应用首先要基于坚实的理论基础和详实的前期研究成果才有意义,如果结构方程模型应用不当,不仅影响数据分析的信度和效度,而且可能产生错误结果误导理论构建或研究结果的实践应用(Ockey&Choi2015)。此外,进行结构方程模型数据分析要先审查样本数据质量是否达到数据分析标准,并根据检验结果和相关理论决定是否进行模型修正。相信随着量化研究在语言学领域的不断深入发展,LISREL结构方程模型统计分析会在我国语言研究中得到越来越广泛的应用。
