锂电池串并联系统可靠性的建模与分析

朱海峰，刘学军，丁 巍，程伟力

(施耐德电气(中国)有限公司上海浦东分公司，上海 201203)

1 简介

世界正处于碳达峰碳中和，构建清洁低碳，安全高效能源体系的大趋势下，中国国家发展改革委，国家能源局也积极推动加快新型储能发展的指导意见。以习近平新时代中国特色社会主义思想为指导，全面贯彻党的十九大和十九届二中、三中、四中、五中全会精神，落实“四个革命、一个合作”能源安全新战略，以实现碳达峰碳中和为目标，将发展新型储能作为提升能源电力系统调节能力、综合效率和安全保障能力，支撑新型电力系统建设的重要举措，以政策环境为有力保障，以市场机制为根本依托，以技术革新为内生动力，加快构建多轮驱动良好局面，推动储能高质量发展。

新型储能的能源形式越来越多样化，其中包括氢能源，电化学能源，机械能源，蓄水能源，光伏能源等，电化学能源使用占比越来越高，锂离子电池就是其中使用最为广泛的电化学能源。

锂电池使用过程中会根据终端产品负载情况，提供电压和电流，保证其按照预期情况运行。在现有技术水平下，电池系统不可避免地需要将大量电池进行串并联组合，以形成更高的电压、更高容量的电池系统，来满足终端应用的要求，如特斯拉model 3需要7 000多节圆柱型电芯进行串并联，国家电网MWh级储能电池系统需要万节级以上电芯串并联。

大量锂离子电池的串并联组合会导致储能电池系统的可靠性降低，那么如何进行电池串并联的设计就是储能电池系统可靠性的关键一环。下面从电池串并联的结构进行数学模型的建立，然后进行简要分析，最后再从实际案例设计，给出单一因素的建议。

2 电池串并联的数学模型建立与分析

2.1 电池的串并联结构

串并联结构模型分为串联结构模型(如图1)、并联结构模型(如图2)，先并后串结构模型(图3)，先串后并结构模型(如图4)，混联结构模型(如图5和图6)。这里需要解释混联结构模型，即超过一次串并联结构的情况，如先并后串再并的结构模型，或者先串后并再串的结构模型。

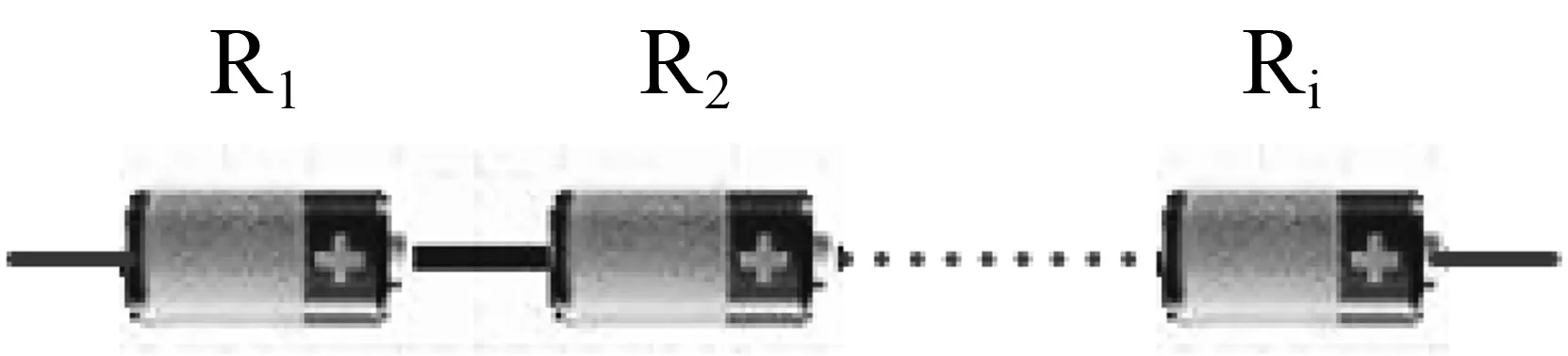
图1 串联结构模型Fig.1 Cell in series model.

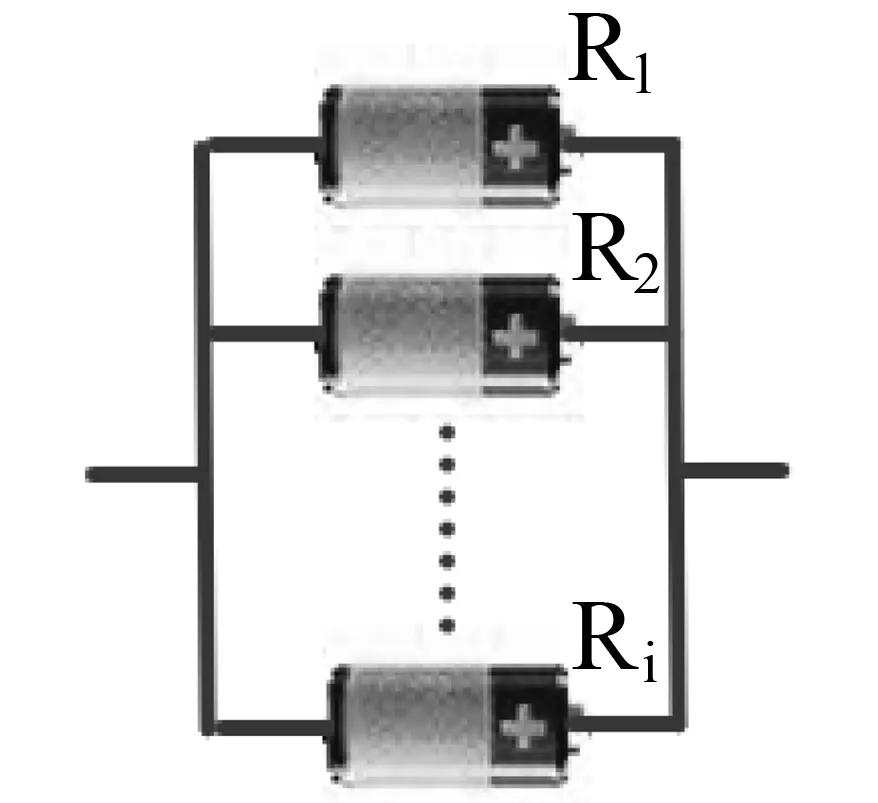
图2 并联结构模型Fig.2 Cell in parallel model.

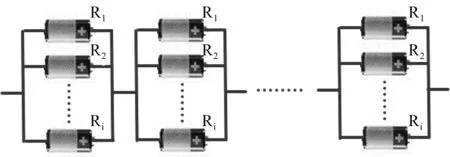
图3 先并联后串联结构模型Fig.3 Cell in parallel before series model.

图4 先串联后并联结构模型Fig.4 Cell in series before parallel model.

图5 混联结构模型(先串联后并联再串联)Fig.5 Hybrid Model (cell in series before parallel then series).

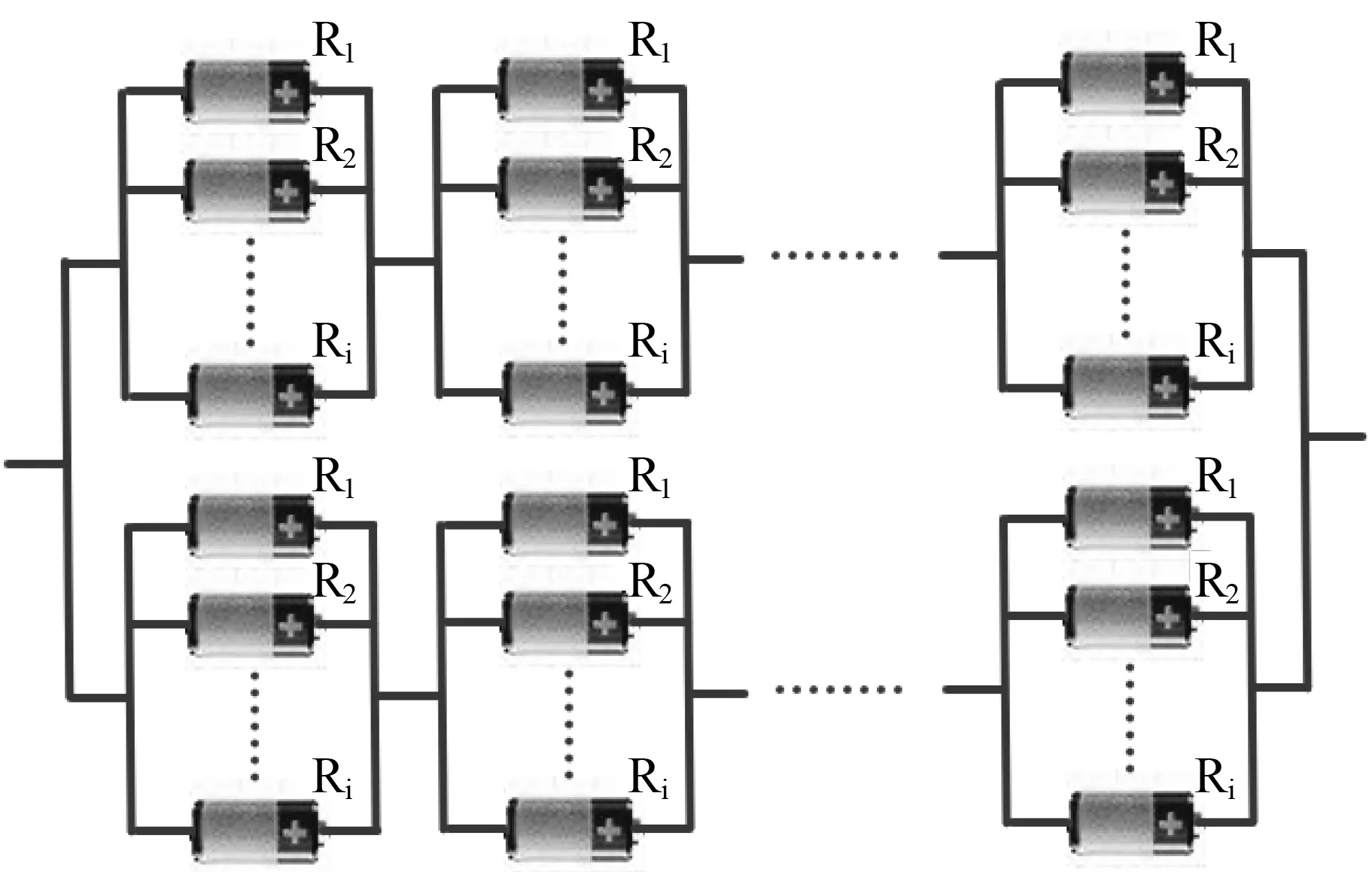
图6 混联结构模型(先并联后串联再并联)Fig.6 Hybrid Model (cell in parallel before series then parallel).

2.2 串并联结构模型的数学模型

假设模型中单体电池出现故障的概率是相同的，并且是相互独立的，不考虑每个单元的复杂程度，环境的严酷程度以及工作时间长短等因素。

Rs(t)表示系统的可靠度，Ri=(1,2,3,……，n)表示第i个单元的可靠度，并且Ri均小于1。m表示并联电池数，n表示串联电池数。

2.2.1 串联结构模型的数学模型

从图1可以看出，串联结构模型是属于单一通道情况，需要每个串联的单元都可靠，整个系统才可靠。所以可得串联结构模型的数学模型为。

从串联结构模型的数学模型可以看出，Rs(t)要小于每一个Ri(t)(n>1)，即在串联结构中，串联单元越多，系统的可靠性越低。

2.2.2 并联结构模型的数学模型

从图2可以看出，并联结构模型是多通道情况，单一单元可靠，整个系统就可靠。所以可得并联结构模型的数学模型。

从并联结构模型的数学模型可以看出，Rs(t)要大于每一个Ri(t)(m>1)，即在并联结构中，并联单元越多，系统的可靠性越高。

2.2.3 先并联后串联结构模型的数学模型

从图3可以看出，先并联后串联结构模型，是二级连接的结构，综合并联和串联的数学模型。所以可得先并联后串联结构模型的数学模型。

从先并联后串结构模型的数学模型可以看出，Rs(t)要小于每一个Ri(t)(n，m>1)，即在先串联后并联结构中，串联单元越少，并联单元越多，系统的可靠性越高。

2.2.4 先串联后并联结构模型的数学模型

从图4可以看出，先串联后并联结构模型是属于二级连接的结构，综合串联和并联的数学模型。所以可得先串联后并联结构模型的数学模型。

从串联后并联结构模型的数学模型可以看出，Rs(t)要小于每一个Ri(t)，(n，m>1)，即在先串联后并联结构中，串联单元越少，并联单元越多，系统的可靠性越高。

2.2.5 混联结构模型的数学模型

从图5可以看出，先串联后并联再串联结构模型是属于三级连接的结构，综合串联和并联的数学模型。所以可得先串联后并联再串联结构模型的数学模型。

从图6可以看出，先并联后串联再并联结构模型是属于三级连接的结构，综合串联和并联的数学模型。所以可得先并联后串联再并联结构模型的数学模型。

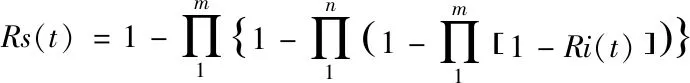
在混联结构模型中，只描述了三级连接的结构。当然，按照模型可以扩展到多级连接结构模型，可以得到有着类似的数学模型。

2.3 储能电池系统可靠性对比示例

一般储能电池系统是由多个电池模块组成的电池柜，电池柜也有可能串并联使用。为了简化可靠性对比，以常见电池模块结构作为示例进行分析。

假设电池模块由64节电芯组成，16节电芯串联和4节电芯并联结构。每节电芯可靠性是一致的。按照电池单体全生命周期顺序0.999 997(6σ)，0.997 3(3σ)，0.954 5(2σ)，0.9，0.8进行计算和比较。电池模块按照四种常见的串并联结构模型分别为4P16S，16S4P，(2P16S)2P，(2P8S)2P2S涵盖二级连接的结构，三级连接的结构和四级连接的结构的主流设计。经计算可以得到表1。

表1 模组可靠性对比示例Table 1 Example of module reliability comparison.

以上数据表格使用0.999 996 6(6σ),0.997 3(3σ)，0.954 5(2σ)，0.9，0.8进行分析，是考虑产品全生命周期，电池的可靠性是随着使用周期，逐步降低的。

从上面数据来看，在不同的电池可靠性数值下，以上四种串并联结构模型的可靠性数值是有很大差异的。电池单体的可靠性越高，系统级别的可靠性越高，并且差异越小。电池单体的可靠性越低，即产品使用的生命周期后段，系统级别可靠性越差，并且差异越大。

3 结论

经过以上锂电池系统使用的串联结构的数学模型，并联结构的数学模型，先并联后串联结构的数学模型，先串联后并联结构的数学模型以及混联结构的数学模型的建立，然后建立实例进行可靠性的计算，从单一变量(电池连接结构差异)考虑和数学模型可以得到如下内容。

(1)针对二级连接方式的结构：

①优先选择先并联后串联结构(先串联后并联结构组成的电池系统可靠性最好)；

②先串联后并联结构组成的电池系统可靠性最差(先串联会导致单路连接的结构可靠性变差)。

(2)三级以上的连接方式的结构：

①n×m级连接结构的可靠性未必比n×m+1级联结结构的可靠性好，即多级连接的可靠性可以通过调整更小级别的模组结构进行优化；

②多级连接方式结构的数学模型的建立，可以根据单级连接结构进行推演，最终获得多级连接结构可靠性的数学模型；

(3)只要锂电池系统中电池的连接方式设计得当，复杂联结结构系统的可靠性未必会比简单联结结构系统的可靠性低，甚至要高，可根据以上数学模型进行单一变量的推演，得到较优方案。