作动筒用O形圈高压工况下动/静密封特性研究*

唐 斌，陈铭亮，王 舒，刘 勇， 赵登辉，黄 巍

(1.国营芜湖机械厂 航空设备测控逆向工程安徽省重点实验室，安徽 芜湖 241007； 2.南京航空航天大学 机电学院，江苏 南京 210016)

0 引 言

作动筒是航空飞行器的重要组成部件，其结构通常由活塞、密封件、筒体等组成。由于制造成本低且性能可靠等优点，O形圈密封在飞行器作动筒液压系统中有着极其广泛的应用。作动筒用密封圈安装在截面为矩形的沟槽内，起密封作用，适用于静密封和往复运动密封[1]。作动筒用密封圈在静密封和动密封过程中常见故障有：介质压力过大使得摩擦力大于轴向力，导致O型圈在沟槽中发生滚动扭转而发生破坏；当压缩率超过使用极限时，O型圈由于应力集中导致破裂等。考虑材料压缩量，为防止出现永久性塑性变形，O形密封圈在静密封中允许的最大压缩量约为30%，在动密封中约为20%[2]。

近年来，国内众多学者对O形圈密封结构开展了大量研究工作[3]。吴广平等[4]运用有限元方法分析了O形橡胶圈剪应力的分布，并探讨了初始压缩量、密封槽口圆角半径、流体压力以及摩擦系数等参数对剪应力的影响；吴琼等[5]设计了往复式标准试验台，以内径190 mm的丁腈橡胶圈为研究对象，分析了不同工况下橡胶圈的摩擦性能；顾东升等[6]研制了一种静环用O形圈性能试验装置，对内径分别为60、70、80 mm的O形丁腈橡胶圈进行静态密封性能测试，分析了各因素对密封圈接触应力和泄漏量的影响。

现代飞行器正向着轻量化、高压化、变压力等方向发展，势必对飞行器作动筒的密封性能和尺寸提出越来越高的要求[7]。为了满足日益高压化、轻量化的作动筒发展趋势，笔者以某系列卡环锁作动筒用小尺寸O形圈为研究对象，探究其在高压工况下的动/静密封特性。利用Ansys建立了作动筒密封结构有限元分析模型，分析了介质工作压力、径向间隙以及密封圈直径等对动/静密封结构性能的影响。模拟O型圈在作动筒中的运动，探究作动筒中O型圈对密封性能的影响，以实现减少现实中作动筒泄露现象的发生。

1 工作原理与前处理设置

1.1 工作原理

图1分别给出了作动筒中的O形密封圈动/静密封结构工作原理。O形圈密封属于一种挤压型密封，其密封的基本工作原理是依靠密封件发生弹性变形并在密封接触面上形成接触压力实现的。当接触压力高于被密封介质的内压时，则不发生泄漏，反之则发生泄漏。对比静密封和动密封，两者的主要区别在于壁面的相对运动。

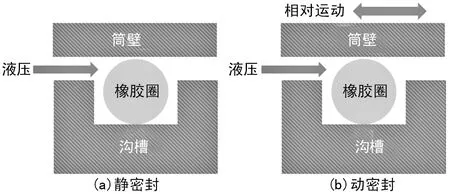
图1 动/静密封结构工作原理

1.2 几何模型

考虑到O形圈密封结构具有轴对称性，因此为了简化计算、提高效率，文中将动/静O形圈密封结构简化为二维轴对称模型来进行分析。同时考虑到丁腈橡胶的可压缩性，在模型网格划分中对接触部分的网格进行细化。文中O形圈密封结构基本尺寸如表1所列，有限元模型网格划分情况如图2所示。

图2 O形圈密封结构有限元模型

表1 O形圈密封结构尺寸

1.3 材料属性

材料属性上，活塞和筒体的材料采用常见的45#钢，O形圈材料为丁腈橡胶(NBR)，其相关材料参数如表2所列。

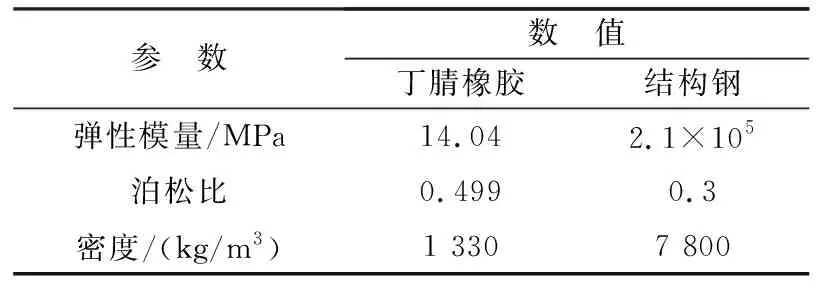
表2 材料参数

丁腈橡胶作为超弹性体材料，在其材料特性上国内外学者提出了多种描述橡胶材料应力-应变关系的应变能函数形式。文中选用Mooney-Rivlin模型描述橡胶超弹性材料在大变形下的力学特性[8]。Mooney-Rivlin模型的2参数弹性应变能函数表达式为：

(1)

式中：W为应变能密度；C10、C01为材料Mooney-Rivlin系数；I1、I2为第一、第二应变张量不变量。因此应力-应变关系即为：

(2)

将Mooney-Rivlin模型的两个参数值C10、C01分别设为1.87和0.47，将其导入Ansys进行绘制，即可得到NBR应力应变曲线，如图3所示。

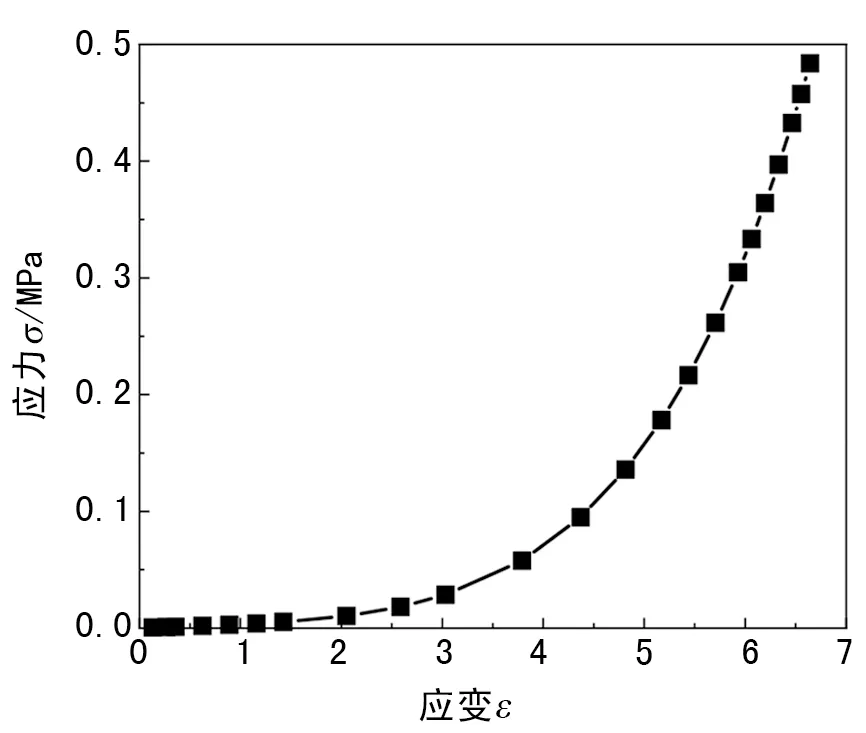
图3 NBR应力应变曲线

1.4 边界条件

如图4所示，在施加油压边界条件后，O形圈与活塞和筒体均有接触。因此文中以筒体和活塞面为目标面，O形圈面为接触面，建立了两对接触，同时考虑安装O形圈时的预压缩现象。在分析时，对应用于静密封的O形圈密封结构，文中将约束及载荷的施加分为两个载荷步，Step1在垂直筒体壁面的方向施加1个位移来模拟O形圈的初始压缩量，Step2在O形圈左侧通过Ansys中的APDL模块施加工作过程中的油压；对于有往复运动的动密封则在Step1上增加平行筒体壁面方向的往复位移。

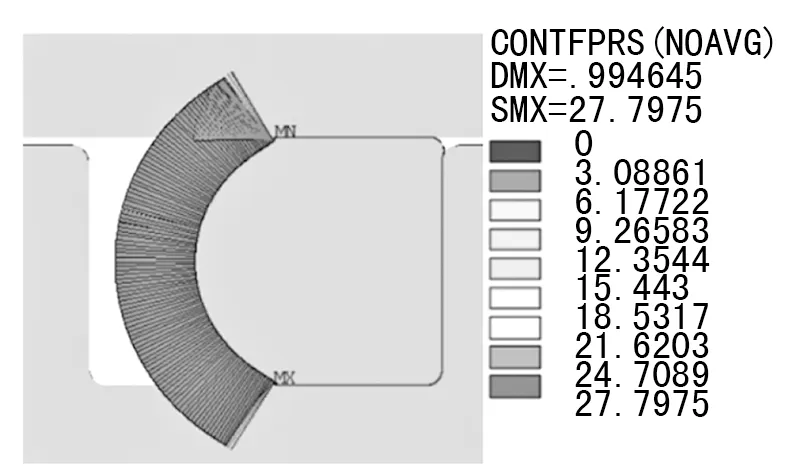
图4 工作油压28 MPa时的边界条件

2 结果分析

2.1 静密封结果分析

通过对28 MPa工作油压下不同压缩率的O形圈静密封进行分析，得到了如图5所示的O形圈静密封的最大变形、接触应力及Von-mises应力云图。从图5(a)不难看出，在高油压工况下，两种压缩率的O形圈都出现了较大的变形，其中5%压缩率的O形圈的变形比20%压缩率的O形圈的变形小了10%左右；并且在5%压缩率时，O形圈在垂直油压方向和低压侧变形较大，最大变形量达到了0.91 mm，发生了挤隙现象。当压缩率为20%时，最大变形量为0.82 mm，主要发生在低压侧内壁处。得益于较高的压缩率，此时并未出现挤隙现象。

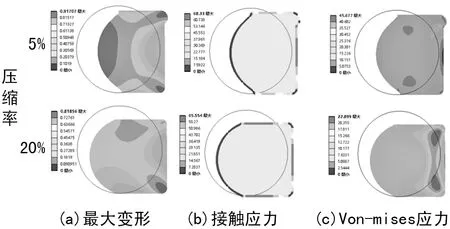
图5 O形圈静密封最大变形、接触应力及Von-mises应力云图

由O形圈密封原理可知，要实现密封功能，其接触处的应力须高于所受的介质压力。接触应力是衡量O形圈密封性能的一个重要指标，图5(b)、(c)给出了O形圈静密封的接触应力及Von-mises应力云图。从图中不难看出，在不同压缩率下接触应力的分布情况类似，最大接触应力位置均出现在密封圈和沟槽壁面接触处。当压缩率为20%时，密封结构接触应力最大为65.5 MPa，比5%压缩率下的最大接触应力低了4%左右。而在Von-mises应力分布上，5%压缩率下由于O形圈挤隙现象较严重，出现了应力集中现象，最大Von-mises应力(45.7 MPa)在O形圈与沟槽壁面转角接触处。

2.2 动密封结果分析

同样，通过对28 MPa工作油压下不同压缩率的O形圈动密封进行分析，得到了如图6所示的O形圈动密封的最大变形、接触应力及Von-mises应力云图。从图6(a)可以看出，在O形圈动密封情况下，随着压缩率的减小，最大变形同样逐渐增大；并且在8%压缩率时O形圈最大变形量达到0.84 mm，同时发生了挤隙现象。

图6 O形圈动密封最大变形、接触应力及Von-mises应力云图

从图6(b)和6(c)同样可以看出，O形圈动密封和静密封一样，在较低压缩率时出现了挤隙和应力集中现象。在8%压缩率下，O形圈动密封在挤隙现象发生处也产生了应力集中现象，最大Von-mises应力达到了38 MPa，并且此压缩率下的O形圈具有较高的最大接触应力(45.9 MPa)。

3 典型参数对密封性能的影响

3.1 工作油压的影响

为了进一步探究工作油压对O形圈密封的影响，文中针对不同压缩率下的相同尺寸O形圈静密封施加了从0～28 MPa的油液压力，得到了如图7所示的油压-最大接触应力变化曲线。由图可以看出，在10 MPa油压以下，最大接触应力均随O形圈工作油压的增加而线性升高；而当工作油压高于10 MPa后，压缩率对O形圈静密封的接触应力起到显著的影响，表现为较低压缩率的O形圈静密封的接触应力会较大。

图7 最大接触应力随油压的变化曲线

3.2 直径的影响

除了工作油压外，O形密封圈直径对密封性能也具有一定影响。图8为工作油压为28 MPa、安装间隙0.1 mm条件下不同直径O形圈在20%压缩率时的动/静密封分析结果。由图可见，随着O形圈直径的增大， 最大Von-mises应力和接触应力均在减小，即：在高压工况下，当压缩率相同时，O形圈的直径越大，最大接触应力和Von-mises应力越小，两者和直径大小呈负相关。

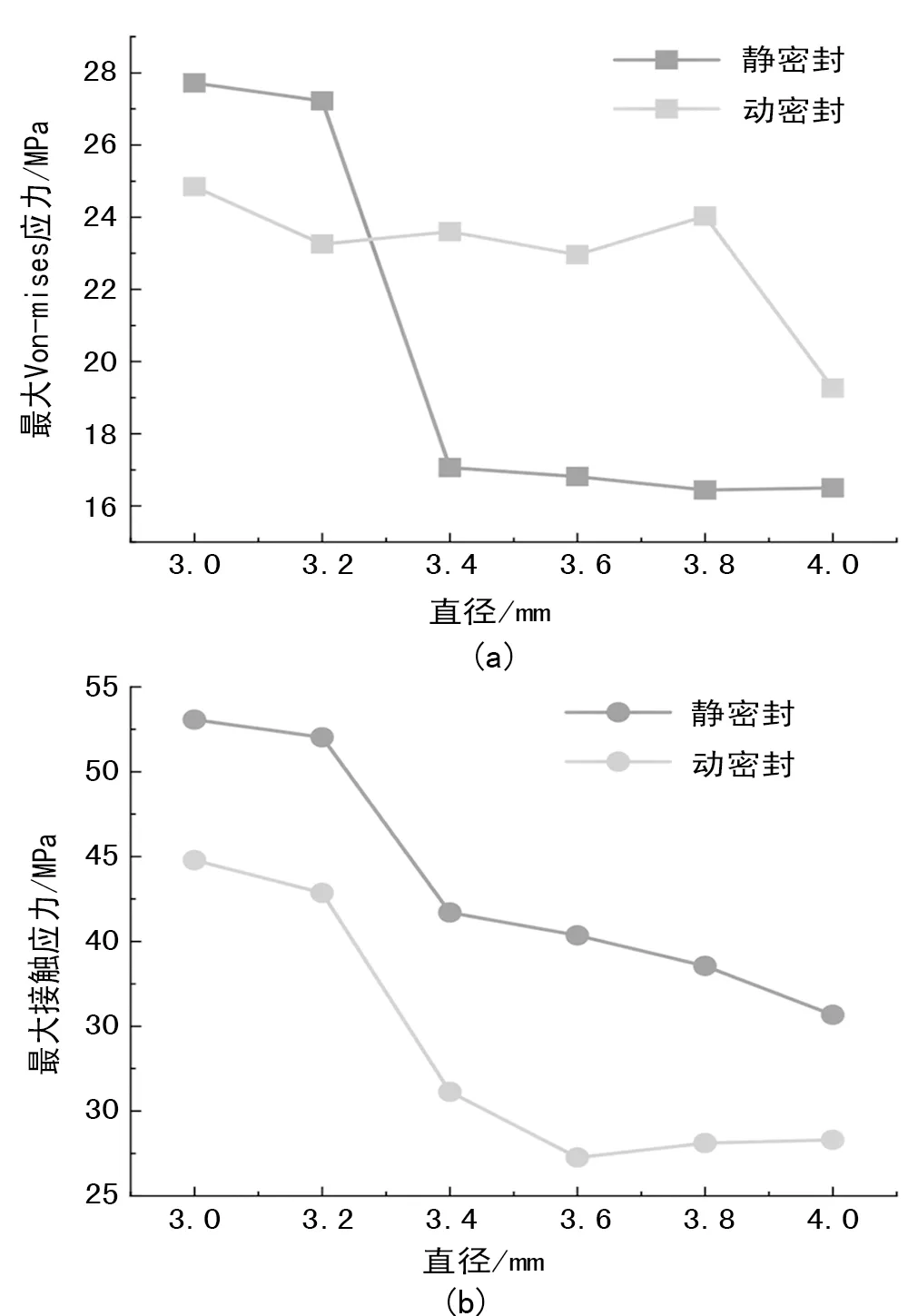
图8 直径-最大Von-mises应力、直径-最大接触应力变化图

4 结 论

针对高压工况下O型密封圈的泄露条件需求，文中重点对影响作动筒中O型圈密封性能的典型因素进行了分析，得出以下结论。

(1) 通过对28 MPa工作油压下不同压缩率的O形圈动/静密封的有限元分析发现，在高压工况下，较高的O形圈压缩率能预防挤隙现象，避免应力集中。

(2) O形圈静密封研究表明，工作油压对密封圈最大接触应力的影响近似呈线性变化；并且在较高油压下，压缩率越高的O形圈密封的最大接触应力越小。

(3) 在高压工况下，当压缩率相同时，无论是动密封还是静密封，O形圈的直径越大，最大接触应力和Von-mises应力均越小，两者和直径大小呈负相关。

此次研究分析了介质工作压力、径向间隙以及密封圈直径对O型圈密封效果的影响，为O形圈密封在飞行器作动筒液压系统的应用提供了依据参考，对于作动筒用O型圈的选用具有重要意义。