BDS/GPS双系统PPP精度分析

刘惠祥

(南昌市城市规划设计研究总院，江西 南昌 330038)

1 引 言

GPS(Global Positioning System)是指利用GPS卫星，向全球各地全天候、大范围地提供高精度实时定位等信息的一种卫星导航和定位系统，北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)是我国自主研制的全球卫星导航系统。

目前，基于导航系统的发展和PPP技术的广泛应用，不少学者对各定位系统精密单点定位精度产生了浓厚的兴趣。邵先锋等[1]采用了静/准动态模式下多系统组合无电离层延迟PPP浮点解与整数钟法固定解的方法对GPS、GLONASS、BDS、GALILEO四种系统进行了实验，相比于单系统，多系统的定位精度提高了10%～30%，增加了定位可靠性。祝会忠等[2]通过PPP技术验证了GPS、BDS、Galileo、GLONASS多系统的定位精度，实验显示多系统组合可以提高定位精度。丁赫等[1]首先通过模拟不同的遮挡环境，证明了BDS/GPS/GLONASS组合系统PPP相较于GPS单系统PPP具有更好的定位性能，并在次年利用整数相位钟法进行了BDS/GPS/GLONASS PPP和单GPS PPP的对比实验，证明组合系统固定解定位精度优于单系统[3]。诸多学者对组合系统与单系统的定位精度进行了研究[5，6]，实验结果皆表明多系统组合能得到优于单系统的定位精度。

上述研究大部分基于BDS与GLONASS组合系统[7]、Galileo与GPS组合系统[8]等，也有学者对BDS/GPS双系统和GPS单系统的定位特征和性能展开研究[9]，本文将基于静态精密单点定位技术对BDS/GPS多系统PPP与GPS单系统PPP定位性能展开研究，以期能对组合系统的定位精度提供参考。

2 BDS/GPS数学模型

GPS单系统载波相位和测码伪距观测的PPP观测方程[1]通过无电离层组合消除电离层延迟影响后，可由式(1)表示：

式中，各符号的含义如表1所示。

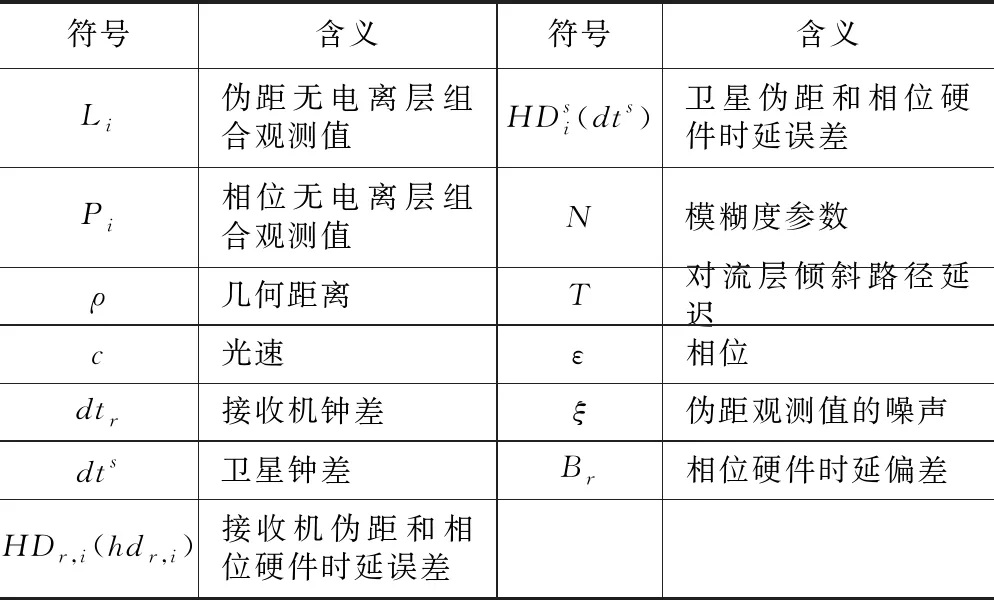
表1 式中各符号的含义

由于北斗单系统的相位与伪距观测方程与GPS单系统类似，且北斗PPP采用了与GPS PPP类似的方法来处理各类参数和误差项，主要流程包括使用Sasstamonion模型改正干分量和估计湿分量，并使用GMF投影函数投影天顶对流层延迟[10]，同时使用精密定轨信息和卫星钟差产品确定卫星轨道和钟差，对观测值中的厘米级以上的系统误差使用模型进行改正。因此，BDS/GPS双系统的无电离层的PPP观测方程可由式(6)表示：

3 数据处理与分析

3.1 数据选取

在进行静态PPP处理时，本文采用以下方案来检验BDS/GPS PPP的定位性能：选择在亚太地区能够同时接收到BDS和GPS观测数据的4个观测站，分别利用GPS单系统和BDS/GPS双系统观测到的数据进行定位精度分析，根据解算得到的定位误差对GPS单系统和BDS/GPS双系统的定位性能进行分析评价。

如图1所示，本文采用的JFNG测站、CMUM测站、GAMG测站、MIZU测站位于90°E-150°E、15°N-45°N的范围内，可获得不同经度和纬度的数据，便于进行单系统和双系统两种非组合PPP模式解算精度的对比分析。

图1 BDS/GPS双系统定位时所用测站的分布图

3.2 处理结果分析

本文使用自编软件按照单系统和双系统定位的模式分别绘制GPS单系统和BDS/GPS双系统的定位误差图，分别如图2、图3所示。图2表示使用单GPS非组合PPP进行定位解算得到在E(东分量)、N(北分量)、U(高程)3个方向分量上的定位误差，JFNG测站的定位误差分别在0.006 m、0.004 m、0.016 m范围内；CMUM测站的定位误差分别在 0.035 m、0.005 m、0.041 m范围内；GAMG测站的定位误差分别在 0.015 m、0.007 m、0.002 m范围内；MIZU测站的定位误差分别在0.026 m、0.005 m、0.017 m范围内。图3表示使用BDS/GPS双系统非组合PPP进行定位精度解算得到在E、N、U 3个方向分量上的定位误差值，JFNG测站的定位误差分别在0.001 m、0.002 m、0.014 m范围内；CMUM测站的定位误差分别在0.024 m、0.004 m、0.025 m范围内；GAMG测站的定位误差分别在0.002 m、0.004 m、0.001 m范围内；MIZU测站的定位误差分别在0.007 m、0.001 m、0.006 m范围内。结合图2、图3可知，BDS/GPS双系统的定位误差在 0.025 m以内，GPS单系统的定位误差在 0.04 m以内，说明双系统比单系统定位误差小、精度高、定位性能优，更适用于高精度定位领域。从图4、图5中可以看出BDS/GPS双系统可视卫星数量较GPS单系统可视卫星数量多，且与GPS单系统相比，BDS/GPS双系统的PDOP值更小，保持在 2 m以内，误差波动较GPS单系统稳定，表明双系统的空间结构较单系统更优。

图2 4个测站的GPS单系统定位误差图

图3 4个测站的BDS/GPS双系统定位误差图

图4 GPS单系统可视卫星数及位置精度因子

图5 BDS/GPS双系统定位误差图可视卫星数及位置精度因子

为了更直观地比较BDS/GPS双系统与GPS单系统定位误差，利用非组合PPP计算出BDS/GPS双系统与GPS单系统在E、N、U方向的误差，并绘制出两种系统单方向误差对比图和单、双系统的定位误差和收敛时间表，分别如图6、表2、表3所示。

从图6中可以看出，在N方向上，JFNG测站在 2 h后趋于稳定，CMUM测站在 7 h后逐渐趋于稳定，GAMG测站在 2 h后逐渐趋于稳定，MIZU测站在 4 h后波动逐渐减小；在E方向上，BDS/GPS双系统的定位精度在4个测站上均与GPS单系统相差不大，BDS/GPS双系统较GPS单系统的定位误差较小，定位精度在CMUM测站显著提高；BDS/GPS双系统PPP的定位误差向真实值收敛的速度较GPS单系统PPP更快，其收敛时间明显短于GPS PPP；在U方向上，每个测站BDS/GPS双系统定位误差均趋向于0，而GPS单系统的定位误差波动较大；JFNG测站、CMUM测站、GAMG测站、MIZU测站分别于0.5 h、6 h、1 h、3 h后波动逐渐减小或趋于稳定值。实验结果表明在E方向上，JFNG、CMUM、CMUM、MIZU测站利用BDS/GPS双系统PPP解算的定位误差略优于GPS单系统。在收敛时间上，BDS/GPS双系统均优于单系统，并且BDS/GPS双系统的定位误差波动更小且随时间增加趋于稳定，说明BDS/GPS双系统具有比GPS单系统更高的稳定性。

图6 GPS单系统与BDS/GPS双系统在E、N、U方向下的定位误差对比

从表2中可以看出，BDS/GPS双系统的定位精度在各个方向都可达到厘米级。在N方向上，单系统与双系统的定位精度都达到了个位数级，但双系统的定位精度更高。4个测站的定位误差均在 0.005 m之内，精度提升分别为：50.0%、20.0%、42.9%、80.0%；在E方向上，每个测站的单系统定位误差都在 0.035 m范围内，而双系统的定位误差在 0.025 m范围内，且定位误差的提升百分比都达到了83.3%、31.4%、86.7%、73.1%；在U方向上，单系统的定位误差在 0.041 m范围之内，双系统的定位误差在 0.025 m范围之内，双系统的定位误差较单系统分别提升了12.5%、39.0%、50.0%、64.7%。

表2 两种定位模式下定位误差对比

从表3中可以看出，在N方向上每个测站的单系统收敛时间分别为：4 h、7 h、2 h、4 h，双系统收敛时间分别为：2 h、6 h、1 h、1 h，较单系统分别提升了50%、14.3%、50%、75%；在E方向上，每个测站的单系统解算收敛时间分别为：1 h、2 h、2 h、2 h，双系统解算收敛时间为0.5 h、2 h、2 h、1 h，较单系统分别提升了50%；在U方向上，每个测站单系统收敛时间分别为 2 h、8 h、3 h、4 h，双系统收敛时间分别为1 h、6 h、2 h、3 h，较单系统分别提升了50%、25%、33.3%、25%。结果显示无论是在水平方向还是在高程方向上，BDS/GPS双系统的定位误差和收敛时间均小于GPS单系统，表明BDS/GPS双系统的定位质量更高，定位结果更可靠。

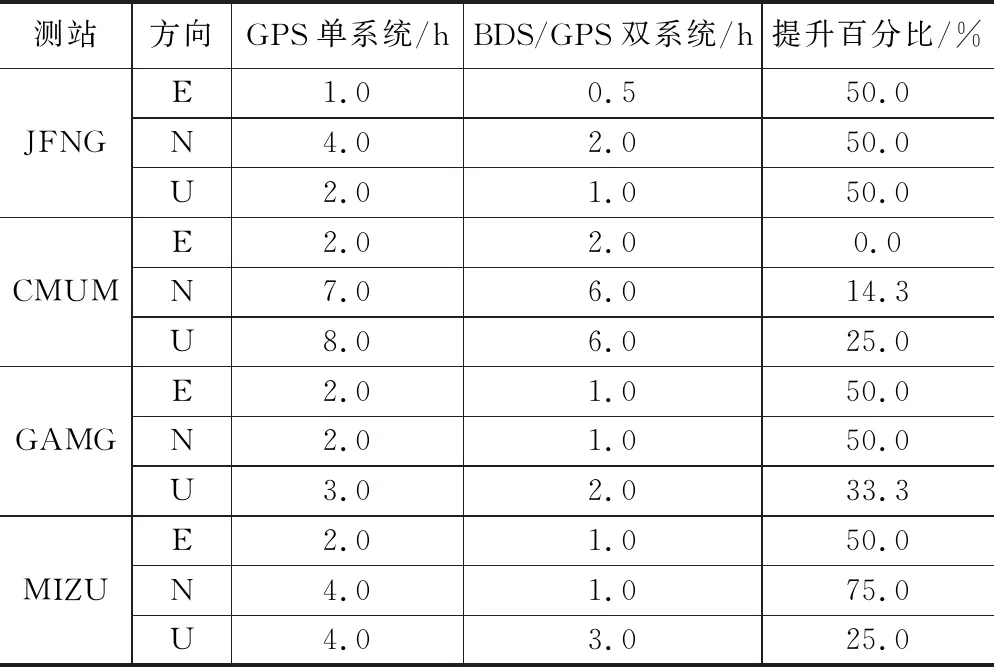
表3 两种定位模式下收敛时间对比

4 结 语

本文采用非组合精密单点定位技术(PPP)研究了BDS/GPS双系统和GPS单系统的定位性能。结果表明：①BDS/GPS双系统与GPS单系统在N方向上的定位误差与收敛时间均优于E方向、U方向；②采用GPS单系统非组合PPP进行定位解算得到的定位误差随时间波动较大，在U方向上的波动较E方向和N方向更为明显，而采用BDS/GPS双系统非组合PPP方法得到的定位误差随时间的波动更小、更稳定；③BDS/GPS双系统在E方向上的定位误差和收敛时间较N方向和U方向提升更高；④BDS/GPS双系统能够观测的卫星数量多于GPS单系统，且双系统GDOP值高，说明BDS/GPS双系统能提供更高精度的定位，适用于对定位质量要求高的领域。