基于时间序列分析法的体育成绩预测

冯其明

(四川文理学院，体育学院， 四川，达州 635000)

0 引言

目前，教育数据预测领域的热点研究方向之一是体育成绩预测研究[1]，以相关已知信息预测未来的学习成绩数据，在成绩、分数、排名等方面均有应用[2]。近年来，在体育精神的弘扬及体育运动员的扩招下，体育教学规模不断变大，导致相关数据及信息不能及时、准确地获取[3]，在很大程度上阻碍了教学质量的提升。在此条件下，分析和研究更可行、更有效率的学生成绩预测方法在体育教学的发展中更有应用性和实践性。

普遍使用的成绩预测方法大体上可分为基于神经网络的预测方法[4]和基于融合知识图谱和协同过滤的预测方法[5]。前者利用神经网络建立预测模型进行目标预测，后者分别使用基于邻节点的方法和基于知识图谱表示学习的方法进行目标预测。两种预测方法在预测过程中均未考虑预测时间序列的非平稳性[6]，导致预测结果存在明显误差。针对这一问题，本文提出了基于时间序列分析法的体育成绩预测方法，有效提升预测结果精度。

1 基于时间序列分析法的体育成绩预测方法

基于时间序列分析法的体育成绩预测原理框图见图1。体育成绩预测过程中，针对体育成绩时间序列的非平稳性，利用奇异值分解滤波算法(SVDFA)将其划分成随机成分和趋势成分。利用GM模型以及PSO-RBFNN(粒子群优化—径向基函数神经网络)模型分别对2种成分进行预测，最终融合两种成分的预测结果，得到体育成绩预测结果。

图1 体育成绩预测原理框图

1.1 奇异值分解滤波算法

SVDFA的主要优势体现在数值稳定性、降维压缩性等方面[7]。因此，利用该算法在贮存的体育成绩记录中优选相关信息时可获取较好的数据分离和去噪效果。矩阵能量分布情况可体现奇异值大小[8]，奇异值对应的成分占据矩阵的比重随着奇异值的变化而变化，并在变化中得出体育成绩数据的趋势信息。若以达成对弱信号的分离和去噪为目的，需运用较大的特征值重组数据[9]。均值化的贮存体育成绩数据序列{A1,A2,…,An}的SVDFA过程如下。

1.1.1 构造矩阵

利用一个N×h的体育成绩数据矩阵描述一组n元数据序列：

(1)

式中，N和h分别等于n-h+1和[(n+1)/2]，[]表示取整。

1.1.2 奇异值分解

存在正交矩阵U∈RN×N、V∈Rh×h和对角阵Σ，运用奇异值分解体育成绩数据序列A可得：

A=UΣVT

(2)

(3)

其中，Δq×q=diag(σ1,σ2,…,σq)，σ1,≥σ1,≥…≥σq>0和q=min(N,h)分别为矩阵A奇异值和秩。

1.1.3 门限控制

将滤波门限设定为η(0<η<1)，在求解关于r的方程时运用最小平方和近似矩阵：

(4)

其中，r为正整数，将q-r个较小的奇异设0，得出：

(5)

由式(5)可得，Δr×r=diag(σ1,σ2,…,σr)。

1.1.4 滤波输出

对矩阵A′=UΣ′VT进行重组，运用求平均的方法对A′中时刻对应元素进行运算[10]，以此得出滤波输出序列{T1,T2,…,Tn}。

1.2 GM(1,1)模型

对已知的体育成绩数据序列A(0)={A(0)(1),A(0)(2),…A(0)(n)}中A(0)一次累计生成，得出生成序列A(1)={A(1)(1),A(1)(2),…A(1)(n)}，由此获取原时间序列：

(6)

此时由A(1)构造背景值序列Z(1)={Z(1)(2),Z(1)(3),…Z(1)(n)},得出：

Z(1)(k)=a′A(1)(k-1)+(1-a′)A(1)(k)

(7)

其中，k=2,3,…,n，发展系数a′=0.5。

若设定A(1)存在近似指数变化规律[11]，可得出白化方程为

(8)

对式(8)进行离散化处理，令其由微分改变为查分，得出GM(1,1)灰微分方程：

A(0)(k)+aZ(1)(k)=i

(9)

由式(9)可知，序列A(0)的增长速度由发展系数a的大小体现，灰作用量(内生变量)为i。为确定式(9)中参数a、i，运用最小二乘法求解式中参数a、i。由此可得出A(1)的预测公式：

(10)

式中，k=0,1,2,…,n。则预测公式A(0)为

(11)

1.3 PSO-RBFNN模型

由输入层、隐含层、输出层组成的RBFNN是前向神经网络[12]。隐含层空间构建是将径向基函数作为隐含层单元的基，以此令数据在低维空间内的线性不可分转换为高维空间中的线性可分[13]。设1为RBFNN内输入层和隐含层的连接权值，隐含层的作用是优化激活函数的参数，输出层的作用是优化连接权值。基函数的中心、隐含层的宽度、隐含层到输出层的连接权值是RBFNN需要求解的3个参数[14]。RBFNN中常用基函数是高斯函数，利用式(12)可表示RBFNN的激活函数：

(12)

式中,输入样本为xp，p=1,2,3,…,N，样本总数为N,隐层网络节点的中心为ci，i=1,2,3,…,H，其中H表示隐含层节点数。

利用式(13)可表示神经网络输出yp：

(13)

高斯函数的方差σ可描述隐含层的宽度参数，RBFNN中的难点为隐含层与输出层权值的确定，可采用粒子群算法确定。利用粒子群算法确定RBFNN内隐含层与输出层权值的过程如图2所示。

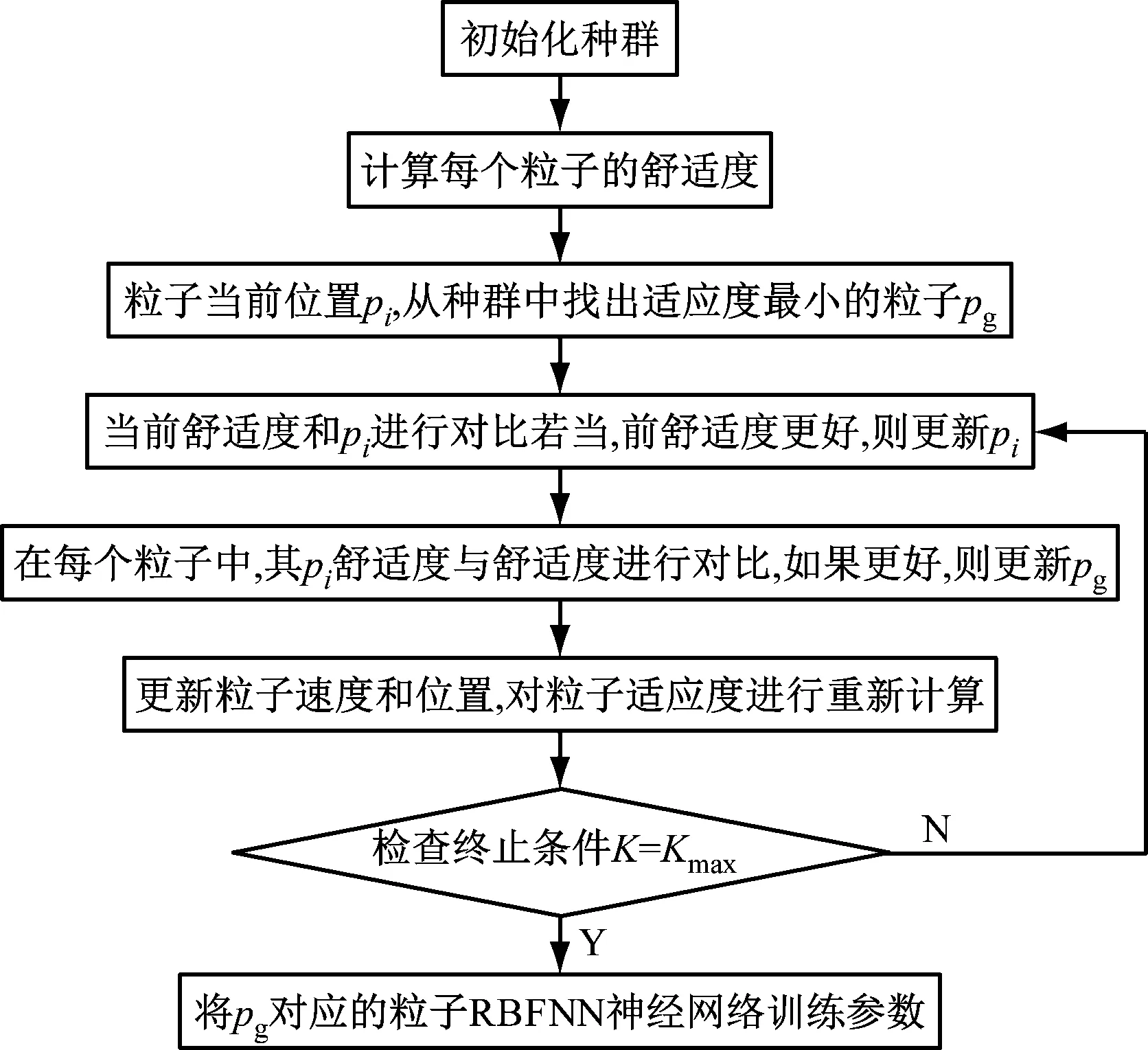
图2 粒子群训练法

1.4 滤波门限算法

滤波的关键是确定门限η，以保证随机成分稳定性为基础，最大限度提升趋势成分的平滑性。具体步骤如下：

(1) 以Δη∈(0,0.01]表示较小步长；

(2) 对滤波门限η=1-Δη进行初始化处理，k=1为循环次数；

(3) 为了分解序列，运用奇异值分解算法，{T1,T2,…,Tn}为趋势成分的标记，{R1,R2,…,Rn}为随机成分标记；

(4) 在检验随机成分的平稳性时选取“逆序”法，如{R1,R2,…,Rn}为不平稳状态，则直接转入步骤(6)；

(5)k=k+1，η=1-k·Δη，重复步骤(3)至步骤(5)；

(6) 获取最终选定的滤波门限η=1-(k-1)·Δη，并输出该值。

2 具体应用实例分析

为验证本文所提出的基于时间序列分析法的体育成绩预测方法的适用性，以某体育学校为研究对象，对本文方法进行实例分析。在研究对象内随机选取1个游泳运动员体育成绩时间序列进行分析，以该体育成绩时间序列内的前50个成绩数据作为样本序列，利用本文方法中的GM(1,1)模型和PSO-RBFNN模型分别实施训练，利用后15个成绩数据检测本文方法的预测性能，预测结果与均方差描述。设定初始Δη为0.003，在本文方法的滤波门限算法下获取η=0.92。利用本文分析获取体育成绩时间序列的趋势成分和随机成分，如图3所示。

利用本文方法中的GM(1,1)模型和PSO-RBFNN模型分别对图3(a)所示的随机成分和图3(b)所示的趋势成分进行预测，综合2个模型的预测结果，即可得到本文方法的最终预测结果。对比本文方法所得预测结果与所选体育成绩时间序列内后15个数据间的均方差，结果如图4所示。分析图4得到，本文方法预测结果的均方差控制在1.54×10-5至2.03×10-5之间，误差均值约为1.78×10-5。实验结果充分说明本文方法能够较高地预测体育成绩。

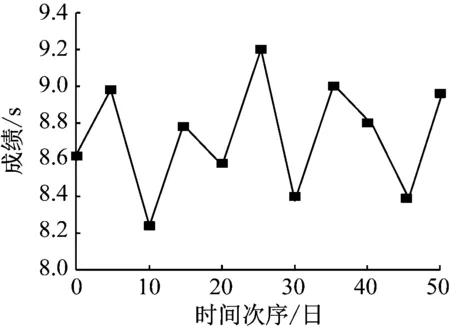
(a) 随机成分

为进一步说明本文方法的预测性能，用文献[4]方法和文献[5]预测方法进行对比实验，利用对比方法对所选体育成绩时间序列进行分析，预测数据序列内后15个数据，所得预测结果的均方差如图5所示。分析图5得到，文献[4]方法和文献[5]方法2种方法预测结果的均方误差分别为2.42×10-5和2.08×10-5。虽然文献[5]方法预测结果的均方差均值低于文献[4]方法，但文献[5]方法预测结果的均方差波动较为剧烈。对比图4和图5中不同预测方法所预测结果的均方差能够得到，本文方法的预测精度显著优于2种对比方法。

图4 本文方法预测结果

图5 对比方法预测结果

采用本文方法进行成绩预测过程中，基于已有数据得到不同η值下的预测结果均方差，所得结果如图6所示。分析图6得到，随着η值的提升，体育成绩预测结果的均方差整体表现为下降趋势。在η值低于6的条件下，本文方法预测结果均方差从1.94×10-5下降至1.8×10-5；当η值由6提升至11时，本文方法预测结果均方差从1.8×10-5下降至1.74×10-5。在η值高于11的条件下，本文方法预测结果均方差维持在1.74×10-5不变。实验结果表明,采用本文方法预测体育成绩，η取值为11时，本文方法预测精度最高。

图6 不同η值下的预测结果均方差

3 总结

为了获得理想的体育成绩预测结果，本文提出了基于时间序列分析法的体育成绩预测方法，分别利用GM模型和PSO-RBFNN模型对时间序列数据的随机成分和趋势成分进行预测，综合预测结果得到最终预测结果，并通过实例分析证明了本文方法的可行性。